数学人教A版(2019)选择性必修第一册2.5.2 圆与圆的位置关系 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.2 圆与圆的位置关系 课件(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 522.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 06:44:22 | ||
图片预览







文档简介
(共20张PPT)
2.5.2 圆与圆的位置关系
1.理解圆与圆的位置的种类;
2.会用代数法、几何法判断两圆的位置关系;(重点、难点);
3.会求两相交圆的公共弦方程、公共弦长.
前面我们运用直线的方程、圆的方程,研究了直线与圆的位置关系.现在我们类比前面的研究方法,利用圆的方程,通过定量计算研究圆与圆的位置关系.
我们知道,两个圆之间存在以下三种位置关系:
(1)两圆相交,有两个公共点;
(2)两圆相切,包括外切和内切,只有一个公共点;
(3)两圆相离,包括外离与内含,没有公共点.
圆与圆的位置关系
思考:类比利用直线与圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的位置关系?
下面,我们通过具体的例子进行研究.
例1 已知圆 和圆 ,判断圆C1 与圆C2 的位置关系.
分析:思路1:圆C1 与圆C2 的位置关系由它们有几个公共点确定,而它们有几个公共点又由它们的方程组成的方程组有几个实数解确定;
思路2:借助图形,可以依据圆心距与两半径的大小关系,判断两圆的位置关系.
解法一:联立圆C1 与圆C2 的方程,得
所以,圆C1 与圆C2有两个公共点,即两圆相交.
作差,得
整理,得
将上式代入①式,得
因为
解法二:圆C1 的方程可化为 ,
其圆心C1 的坐标为(-1,-4),半径长为 ,
则圆心距
圆C2 的方程可化为 ,
其圆心C1 的坐标为(2,2),半径长为 ,
因为, ,
所以有
所以两圆相交.
圆与圆的位置关系判断
已知两圆的方程,则两圆的位置关系的判断有两种方法:
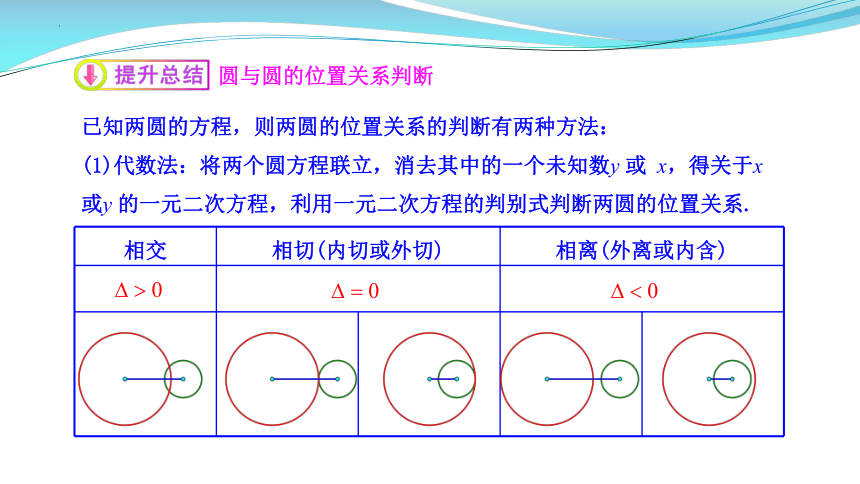
(1)代数法:将两个圆方程联立,消去其中的一个未知数y 或 x,得关于x或y 的一元二次方程,利用一元二次方程的判别式判断两圆的位置关系.
相交 相切(内切或外切) 相离(外离或内含)
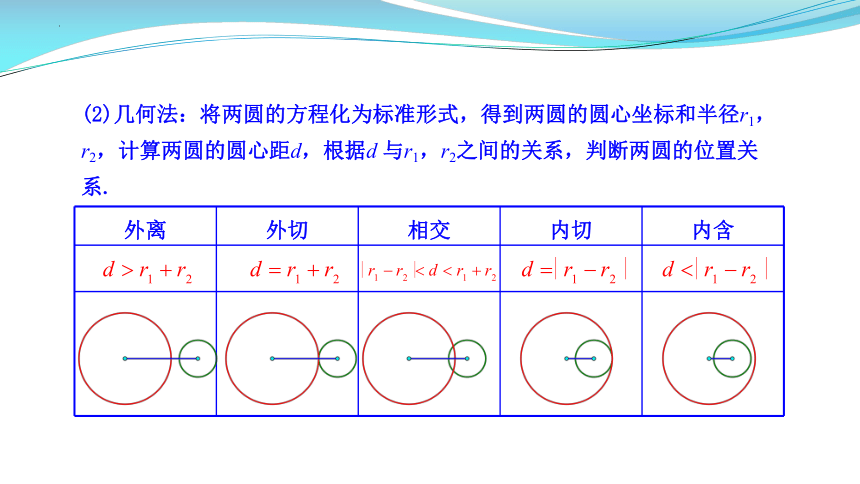
(2)几何法:将两圆的方程化为标准形式,得到两圆的圆心坐标和半径r1,r2,计算两圆的圆心距d,根据d 与r1,r2之间的关系,判断两圆的位置关系.
外离 外切 相交 内切 内含
思考:两种方法的优缺点
几何方法直观,但不能求出交点坐标;
代数方法能求出交点坐标,但当 , 时,不能判断两圆确切的位置关系.
1.判断下列各组圆C1 与圆C2 的位置关系:
(1) , ;
(2) , ;
(3) , .
前面我们求证了圆 与圆
相交,若记两交点为A,B,则线段AB即为公共弦,那如何求公共弦所在直线方程和公共弦长呢?
两圆的公共弦
下面,我们先求两圆公共弦所在直线方程.
探究更一般的情形
若圆 与圆
相交于A,B两点,设 , ,因为点A 在圆C1上,也在圆C2上,那么
① - ② 得
同理点B 在圆C1上,也在圆C2上,可得
由③④可知点A,B 都在直线
上.
显然通过两点的直线只有一条,即直线方程唯一,
故公共弦的方程为
利用结论可得圆
与圆 的相交弦所在直线方程为
下面我们求公共弦长
思路1:解出交点坐标,利用两点间的距离公式求出弦长.
思路2:利用圆的半径、弦心距代入弦长公式求解.
解法一:联立相交弦与圆C1 的方程,得
所以,相交弦的两端点是A(-1,1),B(3,-1).
消去y,得
解得 ,
将 , 分别代入方程①,得 , ,
因此, .
则圆心C(-1,-4)到相交弦距离
解法二:圆C1 的方程可化为 ,
其圆心C 的坐标为(-1,-4),半径长为5,
所以,
例2.已知圆 和圆 相交于A、B 两点,求AB所在的直线方程和公共弦AB的长.
2.已知圆 , 相交于A,B两点,求AB所在的直线方程和公共弦AB的长.
两圆心坐标及半径(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的和与差的大小,下结论
消去y(或x)
几何方法
代数方法
2.5.2 圆与圆的位置关系
1.理解圆与圆的位置的种类;
2.会用代数法、几何法判断两圆的位置关系;(重点、难点);
3.会求两相交圆的公共弦方程、公共弦长.
前面我们运用直线的方程、圆的方程,研究了直线与圆的位置关系.现在我们类比前面的研究方法,利用圆的方程,通过定量计算研究圆与圆的位置关系.
我们知道,两个圆之间存在以下三种位置关系:
(1)两圆相交,有两个公共点;
(2)两圆相切,包括外切和内切,只有一个公共点;
(3)两圆相离,包括外离与内含,没有公共点.
圆与圆的位置关系
思考:类比利用直线与圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的位置关系?
下面,我们通过具体的例子进行研究.
例1 已知圆 和圆 ,判断圆C1 与圆C2 的位置关系.
分析:思路1:圆C1 与圆C2 的位置关系由它们有几个公共点确定,而它们有几个公共点又由它们的方程组成的方程组有几个实数解确定;
思路2:借助图形,可以依据圆心距与两半径的大小关系,判断两圆的位置关系.
解法一:联立圆C1 与圆C2 的方程,得
所以,圆C1 与圆C2有两个公共点,即两圆相交.
作差,得
整理,得
将上式代入①式,得
因为
解法二:圆C1 的方程可化为 ,
其圆心C1 的坐标为(-1,-4),半径长为 ,
则圆心距
圆C2 的方程可化为 ,
其圆心C1 的坐标为(2,2),半径长为 ,
因为, ,
所以有
所以两圆相交.
圆与圆的位置关系判断
已知两圆的方程,则两圆的位置关系的判断有两种方法:
(1)代数法:将两个圆方程联立,消去其中的一个未知数y 或 x,得关于x或y 的一元二次方程,利用一元二次方程的判别式判断两圆的位置关系.
相交 相切(内切或外切) 相离(外离或内含)
(2)几何法:将两圆的方程化为标准形式,得到两圆的圆心坐标和半径r1,r2,计算两圆的圆心距d,根据d 与r1,r2之间的关系,判断两圆的位置关系.
外离 外切 相交 内切 内含
思考:两种方法的优缺点
几何方法直观,但不能求出交点坐标;
代数方法能求出交点坐标,但当 , 时,不能判断两圆确切的位置关系.
1.判断下列各组圆C1 与圆C2 的位置关系:
(1) , ;
(2) , ;
(3) , .
前面我们求证了圆 与圆
相交,若记两交点为A,B,则线段AB即为公共弦,那如何求公共弦所在直线方程和公共弦长呢?
两圆的公共弦
下面,我们先求两圆公共弦所在直线方程.
探究更一般的情形
若圆 与圆
相交于A,B两点,设 , ,因为点A 在圆C1上,也在圆C2上,那么
① - ② 得
同理点B 在圆C1上,也在圆C2上,可得
由③④可知点A,B 都在直线
上.
显然通过两点的直线只有一条,即直线方程唯一,
故公共弦的方程为
利用结论可得圆
与圆 的相交弦所在直线方程为
下面我们求公共弦长
思路1:解出交点坐标,利用两点间的距离公式求出弦长.
思路2:利用圆的半径、弦心距代入弦长公式求解.
解法一:联立相交弦与圆C1 的方程,得
所以,相交弦的两端点是A(-1,1),B(3,-1).
消去y,得
解得 ,
将 , 分别代入方程①,得 , ,
因此, .
则圆心C(-1,-4)到相交弦距离
解法二:圆C1 的方程可化为 ,
其圆心C 的坐标为(-1,-4),半径长为5,
所以,
例2.已知圆 和圆 相交于A、B 两点,求AB所在的直线方程和公共弦AB的长.
2.已知圆 , 相交于A,B两点,求AB所在的直线方程和公共弦AB的长.
两圆心坐标及半径(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的和与差的大小,下结论
消去y(或x)
几何方法
代数方法
