数学人教A版(2019)选择性必修第一册2.4.1 圆的标准方程 课件(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.4.1 圆的标准方程 课件(共16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 491.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 07:23:10 | ||
图片预览






文档简介
(共16张PPT)
2.4 圆的方程
2.4.1 圆的标准方程
1.推导并掌握圆的标准方程;(重点)
2.能根据方程求出圆心及半径;
3.能根据圆心、半径写出圆的标准方程;
4.会用待定系数法求圆的标准方程.(难点)
类似于直线方程的建立过程,为建立圆的方程,我们首先考虑确定一个圆的几何要素. 在平面直角坐标系中,如何确定一个圆呢?
我们知道,圆是平面上到定点的距离等于定长的点的集合. 在平面直角坐标系中,如果一个圆的圆心坐标和半径确定了,圆就唯一确定了. 由此,我们可以建立圆上点的坐标应满足的关系式,进而得到圆的方程.
圆的标准方程
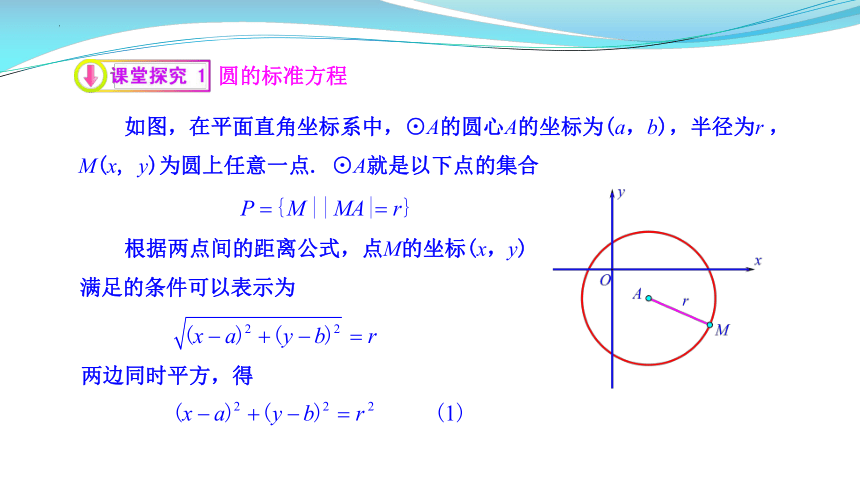
如图,在平面直角坐标系中,⊙A的圆心A的坐标为(a,b),半径为r ,M(x, y)为圆上任意一点. ⊙A就是以下点的集合
根据两点间的距离公式,点M的坐标(x,y)满足的条件可以表示为
两边同时平方,得
由上述过程可知,若点M(x,y)在⊙A上,点M 的坐标就满足方程(1);反过来,若点M 的坐标满足方程(1),就说明点M 在⊙A上.
这时我们把方程
称为圆心为A(a,b),半径为r 的圆的标准方程.
特别地,圆心为O(0,0)的圆的方程为 .
例1.写出下列圆的标准方程:
(1)圆心为(-3,4),半径长是 ,
(2)圆心为(-8,3),且经过点 .
例2 写出圆心为A(2,-3),半径为5的圆的方程,并判断点 ,
与圆的位置关系.
如果设点 到圆心(a,b)的距离为d,则有:
点在圆上 ;
点在圆外 ;
点在圆内 .
点与圆的位置关系
1.若点(1,1)在圆 的内部,则实数a 的取值范围是( )
A. B.
C. 或 D.
A
待定系数法求圆的方程
例3 △AOB的三个顶点的坐标分别是A(4,0),O(0,0),B(0,3),求它的外接圆的方程.
2.求经过点A(1,1)和B(2,-2),且圆心C 在直线 上的圆的标准方程.
1.以(2,-1)为圆心,4为半径的圆的方程为( )
A. B.
C. D.
C
3.圆心在y 轴上,半径为1,且过点(1,2)的圆的标准方程是( )
A. B.
C. D.
A
3.经过点A(1,-1),B(-1,1)且圆心在直线 上的圆的标准方程是( )
A. B.
C. D.
4.已知两点P1(4,9),P2(6,3).
(1)求以P1P2为直径的圆的方程;
(2)试判断点M(6,9),N(3,3),Q(5,3)与(1)中圆的位置关系.
1.圆心为C(a, b),半径为r 的圆的标准方程为
当圆心在原点时,圆的标准方程为:
2.由于圆的标准方程中含有a, b, r三个参数,因此必须具备三个独立的条件才能确定圆;对于由已知条件容易求得圆心坐标和圆的半径或需利用圆心坐标列方程的问题一般采用圆的标准方程。
2.4 圆的方程
2.4.1 圆的标准方程
1.推导并掌握圆的标准方程;(重点)
2.能根据方程求出圆心及半径;
3.能根据圆心、半径写出圆的标准方程;
4.会用待定系数法求圆的标准方程.(难点)
类似于直线方程的建立过程,为建立圆的方程,我们首先考虑确定一个圆的几何要素. 在平面直角坐标系中,如何确定一个圆呢?
我们知道,圆是平面上到定点的距离等于定长的点的集合. 在平面直角坐标系中,如果一个圆的圆心坐标和半径确定了,圆就唯一确定了. 由此,我们可以建立圆上点的坐标应满足的关系式,进而得到圆的方程.
圆的标准方程
如图,在平面直角坐标系中,⊙A的圆心A的坐标为(a,b),半径为r ,M(x, y)为圆上任意一点. ⊙A就是以下点的集合
根据两点间的距离公式,点M的坐标(x,y)满足的条件可以表示为
两边同时平方,得
由上述过程可知,若点M(x,y)在⊙A上,点M 的坐标就满足方程(1);反过来,若点M 的坐标满足方程(1),就说明点M 在⊙A上.
这时我们把方程
称为圆心为A(a,b),半径为r 的圆的标准方程.
特别地,圆心为O(0,0)的圆的方程为 .
例1.写出下列圆的标准方程:
(1)圆心为(-3,4),半径长是 ,
(2)圆心为(-8,3),且经过点 .
例2 写出圆心为A(2,-3),半径为5的圆的方程,并判断点 ,
与圆的位置关系.
如果设点 到圆心(a,b)的距离为d,则有:
点在圆上 ;
点在圆外 ;
点在圆内 .
点与圆的位置关系
1.若点(1,1)在圆 的内部,则实数a 的取值范围是( )
A. B.
C. 或 D.
A
待定系数法求圆的方程
例3 △AOB的三个顶点的坐标分别是A(4,0),O(0,0),B(0,3),求它的外接圆的方程.
2.求经过点A(1,1)和B(2,-2),且圆心C 在直线 上的圆的标准方程.
1.以(2,-1)为圆心,4为半径的圆的方程为( )
A. B.
C. D.
C
3.圆心在y 轴上,半径为1,且过点(1,2)的圆的标准方程是( )
A. B.
C. D.
A
3.经过点A(1,-1),B(-1,1)且圆心在直线 上的圆的标准方程是( )
A. B.
C. D.
4.已知两点P1(4,9),P2(6,3).
(1)求以P1P2为直径的圆的方程;
(2)试判断点M(6,9),N(3,3),Q(5,3)与(1)中圆的位置关系.
1.圆心为C(a, b),半径为r 的圆的标准方程为
当圆心在原点时,圆的标准方程为:
2.由于圆的标准方程中含有a, b, r三个参数,因此必须具备三个独立的条件才能确定圆;对于由已知条件容易求得圆心坐标和圆的半径或需利用圆心坐标列方程的问题一般采用圆的标准方程。
