数学人教A版(2019)选择性必修第一册2.2.2 直线的两点式方程 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.2 直线的两点式方程 课件(共15张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 497.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 07:25:17 | ||
图片预览






文档简介
(共15张PPT)
2.2.2 直线的两点式方程
1.掌握直线方程的两点式的形式特点及适用范围; (重点、难点 )
2.了解直线方程截距式的形式特点及适用范围;
3.通过四种形式方程的对比,掌握类比思想.
已知直线经过P1(1,3)和P2(2,4)两点,求直线的方程.
解:由斜率公式得到斜率
再由点斜式方程得
化简可得
已知两点 ,求通过这两点的直线方程.
直线的两点式方程
解:经过两点P1 , P2的直线斜率
整理可得:
任取P1 , P2中的一点,例如取点P1(x1,y1),由点斜式方程,得
我们把上式称为直线的两点式方程,简称两点式.
若点 中有 ,或 ,此时过这两点的直线方程是什么
当x1=x2时方程为:x-x1=0或x=x1
当y1= y2时方程为:y-y1=0或y=y1
例1.求过下列两点的直线的两点式方程
(1)P1(2,1),P2(0,-3);
(2)A(0,5),B(5,0).
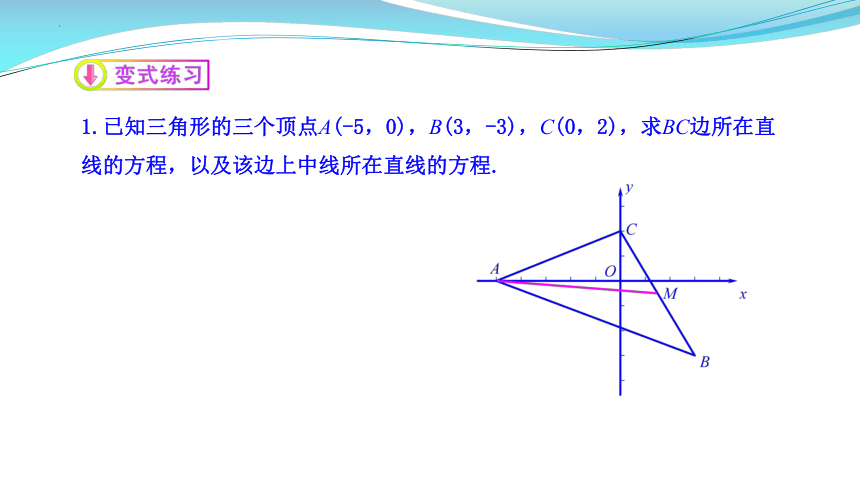
1.已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2),求BC边所在直线的方程,以及该边上中线所在直线的方程.
x
l
B(0,b)
A(a,0)
O
y
解:将A(a,0),B(0,b)的坐标代入两点式得:
已知直线l 与x 轴的交点为A(a,0),与y 轴的交点为B(0,b),其中a≠0,b≠0,求直线l 的方程.
直线的截距式方程
我们把上式叫做直线的截距式方程,简称截距式.
化简得
例2 求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
O
x
y
分析:截距均为0时,设方程为y=kx,
截距均不为0时,设为截距式求解.
解:①当截距均为0时,设方程为 ,
把P(-5,4)代入上式得 ,
即直线方程为 .
②当截距均不为0时,设直线方程为 ,
把P(-5,4)代入上式得 .
直线方程为 ,
即 .
综上:直线方程为 或 .
截距为零不容忽视
直线过原点不容忽视
2.求过点(2,1)且在x 轴上的截距是在y 轴上截距2倍的直线方程.
解:若直线过原点,满足条件,方程为 ;
若直线不过原点,设直线方程为
代入点(2,1),得
解得 ,方程为 .
综上:直线方程为 或 .
直线方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
斜率存在
斜率存在
斜率存在且不为0
斜率存在且不为0,不过原点
各类方程的适用范围
1.根据下列条件求直线方程
(1)在x轴上的截距是2,在y轴上的截距是3;
(2)在x轴上的截距是-5,在y轴上的截距是6.
2.根据下列条件求直线方程
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
3.求经过点(1,2),并且和两坐标轴正半轴围成的三角形面积是4的直线方程.
1.直线的两点式方程
2.截距式方程
两点式适用于与两坐标轴不垂直的直线.
截距式适用于横、纵截距都存在且都不为0的直线.
3.中点坐标公式
2.2.2 直线的两点式方程
1.掌握直线方程的两点式的形式特点及适用范围; (重点、难点 )
2.了解直线方程截距式的形式特点及适用范围;
3.通过四种形式方程的对比,掌握类比思想.
已知直线经过P1(1,3)和P2(2,4)两点,求直线的方程.
解:由斜率公式得到斜率
再由点斜式方程得
化简可得
已知两点 ,求通过这两点的直线方程.
直线的两点式方程
解:经过两点P1 , P2的直线斜率
整理可得:
任取P1 , P2中的一点,例如取点P1(x1,y1),由点斜式方程,得
我们把上式称为直线的两点式方程,简称两点式.
若点 中有 ,或 ,此时过这两点的直线方程是什么
当x1=x2时方程为:x-x1=0或x=x1
当y1= y2时方程为:y-y1=0或y=y1
例1.求过下列两点的直线的两点式方程
(1)P1(2,1),P2(0,-3);
(2)A(0,5),B(5,0).
1.已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2),求BC边所在直线的方程,以及该边上中线所在直线的方程.
x
l
B(0,b)
A(a,0)
O
y
解:将A(a,0),B(0,b)的坐标代入两点式得:
已知直线l 与x 轴的交点为A(a,0),与y 轴的交点为B(0,b),其中a≠0,b≠0,求直线l 的方程.
直线的截距式方程
我们把上式叫做直线的截距式方程,简称截距式.
化简得
例2 求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
O
x
y
分析:截距均为0时,设方程为y=kx,
截距均不为0时,设为截距式求解.
解:①当截距均为0时,设方程为 ,
把P(-5,4)代入上式得 ,
即直线方程为 .
②当截距均不为0时,设直线方程为 ,
把P(-5,4)代入上式得 .
直线方程为 ,
即 .
综上:直线方程为 或 .
截距为零不容忽视
直线过原点不容忽视
2.求过点(2,1)且在x 轴上的截距是在y 轴上截距2倍的直线方程.
解:若直线过原点,满足条件,方程为 ;
若直线不过原点,设直线方程为
代入点(2,1),得
解得 ,方程为 .
综上:直线方程为 或 .
直线方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
斜率存在
斜率存在
斜率存在且不为0
斜率存在且不为0,不过原点
各类方程的适用范围
1.根据下列条件求直线方程
(1)在x轴上的截距是2,在y轴上的截距是3;
(2)在x轴上的截距是-5,在y轴上的截距是6.
2.根据下列条件求直线方程
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
3.求经过点(1,2),并且和两坐标轴正半轴围成的三角形面积是4的直线方程.
1.直线的两点式方程
2.截距式方程
两点式适用于与两坐标轴不垂直的直线.
截距式适用于横、纵截距都存在且都不为0的直线.
3.中点坐标公式
