2.1.1 倾斜角与斜率数学人教A版(2019)选择性必修第一册(共27张ppt)
文档属性
| 名称 | 2.1.1 倾斜角与斜率数学人教A版(2019)选择性必修第一册(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 674.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第二章 直线和圆的方程
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
1.正确理解直线的倾斜角和斜率的概念;(重点)
2.理解直线的倾斜角的唯一性;
3.理解直线的斜率的存在性;(难点)
4.了解斜率公式的推导过程,掌握过两点的直线斜率公式.(重点、难点)
为了研究角的需要,我们常在平面直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,逆时针进行旋转,角的终边在第几象限,我们就说这个角是第几象限的角.
象限角
O
x
y
O
x
y
若点P(x,y)为角α 终边上任意一点,则
P(x,y)
O
x
y
任意角的三角函数
α
tanx 的函数图象
函数 在 上单调递增,函数值为正,且从0增大到 ;在 上单调递增,函数值为负,且从 增大到0.
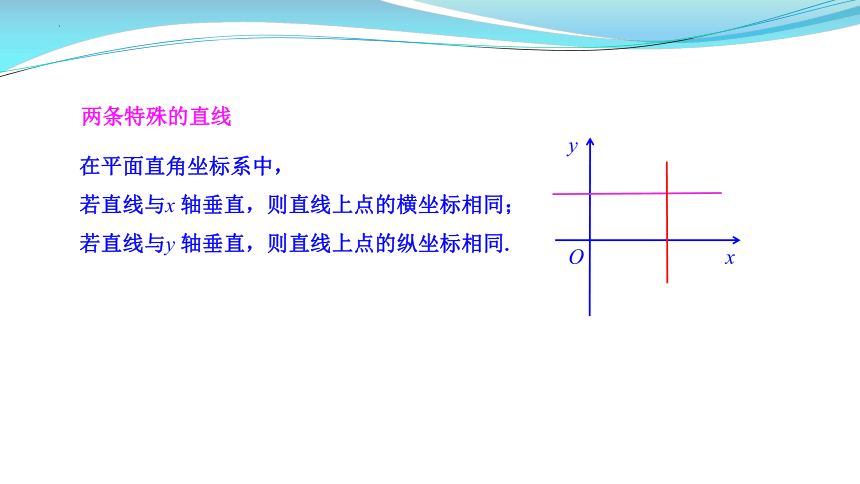
两条特殊的直线
在平面直角坐标系中,
若直线与x 轴垂直,则直线上点的横坐标相同;
若直线与y 轴垂直,则直线上点的纵坐标相同.
y
O
x
勒奈·笛卡尔(René Descartes,1596-1650):法国数学家、科学家和哲学家,堪称17世纪以来欧洲哲学界和科学界最有影响的巨匠之一,被誉为“近代科学的始祖”.
坐标法:以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.
几何
代数
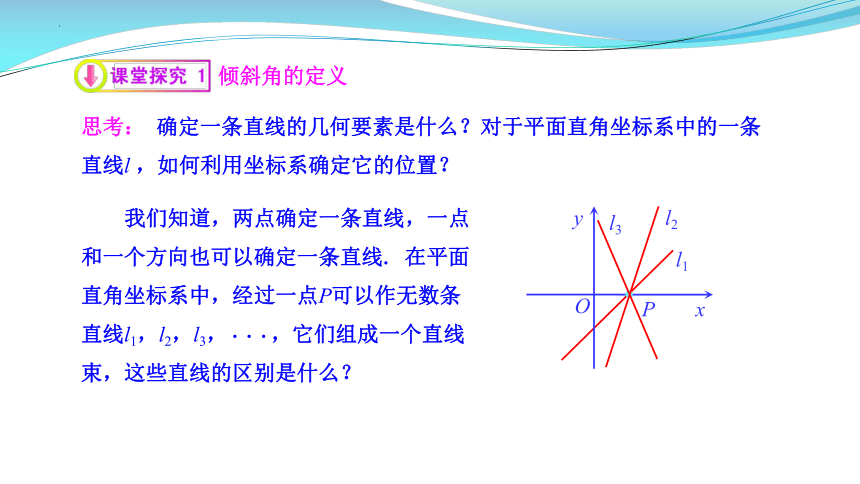
思考: 确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线l ,如何利用坐标系确定它的位置?
l1
y
x
O
P
倾斜角的定义
我们知道,两点确定一条直线,一点和一个方向也可以确定一条直线. 在平面直角坐标系中,经过一点P可以作无数条直线l1,l2,l3,···,它们组成一个直线束,这些直线的区别是什么?
l2
l3
我们看到,这些直线相对于x 轴的倾斜程度不同,也就是它们与x 轴所成的角不同. 因此,我们可以利用这样的角表示这些直线的方向.
在平面直角坐标系中,我们规定水平直线的方向向右,其它直线向上的方向为这条直线的方向. 因此这些直线的区别是它们的方向不同. 如何表示这些直线的方向?
x
O
y
l1
P
l2
l3
当直线l 与x 轴相交时,我们以x 轴为基准,x 轴正向与直线l 向上的方向之间所成的角α 叫做直线l 的倾斜角. 图中,直线l1的倾斜角为锐角,直线l3 的倾斜角为钝角. 当直线l 与x 轴平行或重合时,我们规定它的倾斜角为0°.
x
O
y
l1
P
l2
l3
直线的倾斜角α的范围为:
例1 (多选)下列命题中,正确的是( )
A.任意一条直线都有唯一的倾斜角
B.一条直线的倾斜角可以为-30°
C.倾斜角为0°的直线有无数条
D.若直线的倾斜角为α,则sin α∈(0,1)
直线斜率的定义
设 , ,(其中 )是直线l 上的两点. 由两点确定一条直线可知,直线l 由点P1,P2唯一确定. 所以,可以推断,直线l 的倾斜角一定与P1,P2两点的坐标有关. 那该如何去描述这种关系呢?
思考:在平面直角坐标系中,设直线l 的倾斜角为α.
(1)已知直线l 经过点 , ,α 与O,P的坐标有什么关系?
(2)如果直线l 经过 , ,α 与P1,P2的坐标又有什么关系?
(3)一般地,如果直线l 经过 , , ,那么α 与P1,P2的坐标有怎样的关系?
如图,向量 ,直线OP的倾斜角为α. 由正切函数的定义,有
(1)已知直线l 经过点 , ,α 与O,P的坐标有什么关系?
x
O
y
α
如图,向量 ,平移向量 到 ,则点P的坐标为,且直线OP的倾斜角也是α. 由正切函数的定义,有
(2)如果直线l 经过 , ,α 与P1,P2的坐标又有什么关系?
x
O
y
α
如图,当向量 的方向向上时, ,平移向量 到 ,则点P 的坐标为 ,且直线OP的倾斜角也是α. 由正切函数的定义,有
x
O
y
α
(3)一般地,如果直线l 经过 , , ,那么α 与P1,P2的坐标有怎样的关系?
同样,当向量 的方向向上时,如图, ,也有
x
O
y
α
思考:当直线与x 轴平行时,上述式子还成立吗?为什么?
我们把一条直线的倾斜角α 的正切值叫做这条直线的斜率. 斜率常用小写字母k 表示,即
综上可知,直线l 的倾斜角α 与直线l 上的两点 ,
的坐标有如下关系:
例如:倾斜角 时,直线的斜率 ;倾斜角 时,直线的斜率 .
例2 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
O
x
y
A
C
B
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB与CA的倾斜角均为锐角;
由 知,直线BC的倾斜角为钝角.
斜率为正,倾斜角为锐角;
斜率为负,倾斜角为钝角;
斜率为0,倾斜角为0°;
斜率不存在时,倾斜角为直角.
我们发现,在平面直角坐标系中,倾斜角和斜率分别从形和数两个角度刻画了直线相对于x 轴的倾斜程度.
注:(1)直线的倾斜角为90°时, ,此时直线的斜率不存在.
(2)当直线的倾斜角由0°逐渐增大到90°时,斜率k由 ,再由90°增大到180°时,斜率k 由 .
(3)斜率公式与两点坐标的顺序无关.
直线的方向向量与斜率的关系:
若直线l 的斜率为k,它的一个方向向量的坐标为(x,y),则 .
特别地,当方向向量的横坐标为1时,纵坐标就是斜率k .
证明:取直线上任意两点 , ,则直线的一个方向向量为 ,可以发现 .
1.已知下列直线的倾斜角,求直线的斜率.
(1) (2) (3) (4)
2.已知下列直线的斜率,求直线的倾斜角.
(1) (2) (3) (4)
2.判断经过下列两点的直线的斜率是否存在?如果存在,求其斜率.
(1) A(2,3),B(4,5); (2) C(-2,3),D(2,-1);
(3) P(-3,1),Q(-3,10); (4) M(a,2),N(3,6).
3.已知直线l 的方向向量的坐标为(1, ),则直线l 的倾斜角为________.
4.已知直线l 经过两点A(-1,m),B(m,1),问:当m取何值时:
(1)直线与x 轴平行;
(2)直线与y 轴平行;
(3)直线的方向向量的坐标为(3,1);
(4)直线的倾斜角为45°;
(5)直线的倾斜角为锐角.
5.已知直线l 过P(-2,-1),且与以A(-4,2),B(1,3)为端点的线段相交,求直线l 的斜率的取值范围.
1.直线倾斜角的定义及其范围:
2.斜率k与倾斜角 之间的关系:
3.斜率公式:
“几何问题代数化”的思想
第二章 直线和圆的方程
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
1.正确理解直线的倾斜角和斜率的概念;(重点)
2.理解直线的倾斜角的唯一性;
3.理解直线的斜率的存在性;(难点)
4.了解斜率公式的推导过程,掌握过两点的直线斜率公式.(重点、难点)
为了研究角的需要,我们常在平面直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,逆时针进行旋转,角的终边在第几象限,我们就说这个角是第几象限的角.
象限角
O
x
y
O
x
y
若点P(x,y)为角α 终边上任意一点,则
P(x,y)
O
x
y
任意角的三角函数
α
tanx 的函数图象
函数 在 上单调递增,函数值为正,且从0增大到 ;在 上单调递增,函数值为负,且从 增大到0.
两条特殊的直线
在平面直角坐标系中,
若直线与x 轴垂直,则直线上点的横坐标相同;
若直线与y 轴垂直,则直线上点的纵坐标相同.
y
O
x
勒奈·笛卡尔(René Descartes,1596-1650):法国数学家、科学家和哲学家,堪称17世纪以来欧洲哲学界和科学界最有影响的巨匠之一,被誉为“近代科学的始祖”.
坐标法:以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.
几何
代数
思考: 确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线l ,如何利用坐标系确定它的位置?
l1
y
x
O
P
倾斜角的定义
我们知道,两点确定一条直线,一点和一个方向也可以确定一条直线. 在平面直角坐标系中,经过一点P可以作无数条直线l1,l2,l3,···,它们组成一个直线束,这些直线的区别是什么?
l2
l3
我们看到,这些直线相对于x 轴的倾斜程度不同,也就是它们与x 轴所成的角不同. 因此,我们可以利用这样的角表示这些直线的方向.
在平面直角坐标系中,我们规定水平直线的方向向右,其它直线向上的方向为这条直线的方向. 因此这些直线的区别是它们的方向不同. 如何表示这些直线的方向?
x
O
y
l1
P
l2
l3
当直线l 与x 轴相交时,我们以x 轴为基准,x 轴正向与直线l 向上的方向之间所成的角α 叫做直线l 的倾斜角. 图中,直线l1的倾斜角为锐角,直线l3 的倾斜角为钝角. 当直线l 与x 轴平行或重合时,我们规定它的倾斜角为0°.
x
O
y
l1
P
l2
l3
直线的倾斜角α的范围为:
例1 (多选)下列命题中,正确的是( )
A.任意一条直线都有唯一的倾斜角
B.一条直线的倾斜角可以为-30°
C.倾斜角为0°的直线有无数条
D.若直线的倾斜角为α,则sin α∈(0,1)
直线斜率的定义
设 , ,(其中 )是直线l 上的两点. 由两点确定一条直线可知,直线l 由点P1,P2唯一确定. 所以,可以推断,直线l 的倾斜角一定与P1,P2两点的坐标有关. 那该如何去描述这种关系呢?
思考:在平面直角坐标系中,设直线l 的倾斜角为α.
(1)已知直线l 经过点 , ,α 与O,P的坐标有什么关系?
(2)如果直线l 经过 , ,α 与P1,P2的坐标又有什么关系?
(3)一般地,如果直线l 经过 , , ,那么α 与P1,P2的坐标有怎样的关系?
如图,向量 ,直线OP的倾斜角为α. 由正切函数的定义,有
(1)已知直线l 经过点 , ,α 与O,P的坐标有什么关系?
x
O
y
α
如图,向量 ,平移向量 到 ,则点P的坐标为,且直线OP的倾斜角也是α. 由正切函数的定义,有
(2)如果直线l 经过 , ,α 与P1,P2的坐标又有什么关系?
x
O
y
α
如图,当向量 的方向向上时, ,平移向量 到 ,则点P 的坐标为 ,且直线OP的倾斜角也是α. 由正切函数的定义,有
x
O
y
α
(3)一般地,如果直线l 经过 , , ,那么α 与P1,P2的坐标有怎样的关系?
同样,当向量 的方向向上时,如图, ,也有
x
O
y
α
思考:当直线与x 轴平行时,上述式子还成立吗?为什么?
我们把一条直线的倾斜角α 的正切值叫做这条直线的斜率. 斜率常用小写字母k 表示,即
综上可知,直线l 的倾斜角α 与直线l 上的两点 ,
的坐标有如下关系:
例如:倾斜角 时,直线的斜率 ;倾斜角 时,直线的斜率 .
例2 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
O
x
y
A
C
B
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB与CA的倾斜角均为锐角;
由 知,直线BC的倾斜角为钝角.
斜率为正,倾斜角为锐角;
斜率为负,倾斜角为钝角;
斜率为0,倾斜角为0°;
斜率不存在时,倾斜角为直角.
我们发现,在平面直角坐标系中,倾斜角和斜率分别从形和数两个角度刻画了直线相对于x 轴的倾斜程度.
注:(1)直线的倾斜角为90°时, ,此时直线的斜率不存在.
(2)当直线的倾斜角由0°逐渐增大到90°时,斜率k由 ,再由90°增大到180°时,斜率k 由 .
(3)斜率公式与两点坐标的顺序无关.
直线的方向向量与斜率的关系:
若直线l 的斜率为k,它的一个方向向量的坐标为(x,y),则 .
特别地,当方向向量的横坐标为1时,纵坐标就是斜率k .
证明:取直线上任意两点 , ,则直线的一个方向向量为 ,可以发现 .
1.已知下列直线的倾斜角,求直线的斜率.
(1) (2) (3) (4)
2.已知下列直线的斜率,求直线的倾斜角.
(1) (2) (3) (4)
2.判断经过下列两点的直线的斜率是否存在?如果存在,求其斜率.
(1) A(2,3),B(4,5); (2) C(-2,3),D(2,-1);
(3) P(-3,1),Q(-3,10); (4) M(a,2),N(3,6).
3.已知直线l 的方向向量的坐标为(1, ),则直线l 的倾斜角为________.
4.已知直线l 经过两点A(-1,m),B(m,1),问:当m取何值时:
(1)直线与x 轴平行;
(2)直线与y 轴平行;
(3)直线的方向向量的坐标为(3,1);
(4)直线的倾斜角为45°;
(5)直线的倾斜角为锐角.
5.已知直线l 过P(-2,-1),且与以A(-4,2),B(1,3)为端点的线段相交,求直线l 的斜率的取值范围.
1.直线倾斜角的定义及其范围:
2.斜率k与倾斜角 之间的关系:
3.斜率公式:
“几何问题代数化”的思想
