人教版八年级下册第十八章 平行四边形《折纸做60°,30°,15°的角》教学设计(共25张PPT)
文档属性
| 名称 | 人教版八年级下册第十八章 平行四边形《折纸做60°,30°,15°的角》教学设计(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 18.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 13:24:37 | ||
图片预览





文档简介
(共25张PPT)
版本学科:人教版·初中数学·八年级下册
授课题目:《第十八章 数学活动——
折纸做60°,30°,15°的角》
创设情境
折纸艺术
人教版·初中数学·八年级下册
第十八章 数学活动
——折纸做60°,30°,15°的角
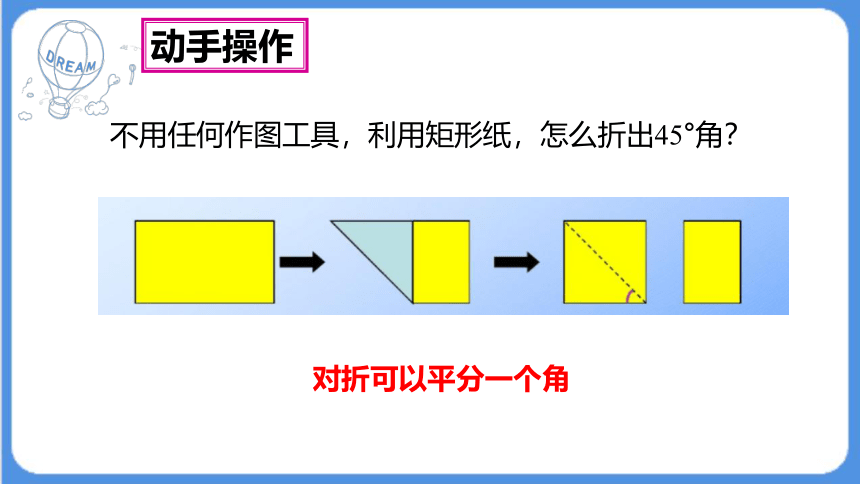
不用任何作图工具,利用矩形纸,怎么折出45°角?
对折可以平分一个角
动手操作
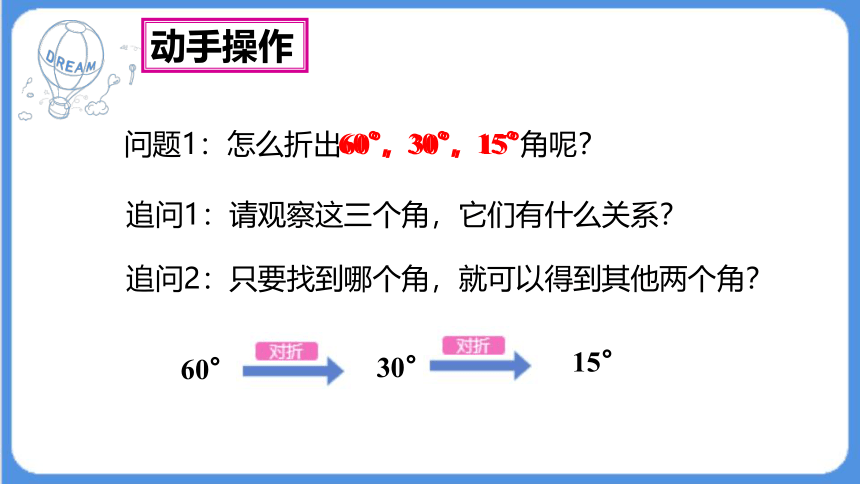
问题1:怎么折出60°,30°,15°角呢?
追问1:请观察这三个角,它们有什么关系?
追问2:只要找到哪个角,就可以得到其他两个角?
60°
30°
15°
60°,30°,15°
动手操作
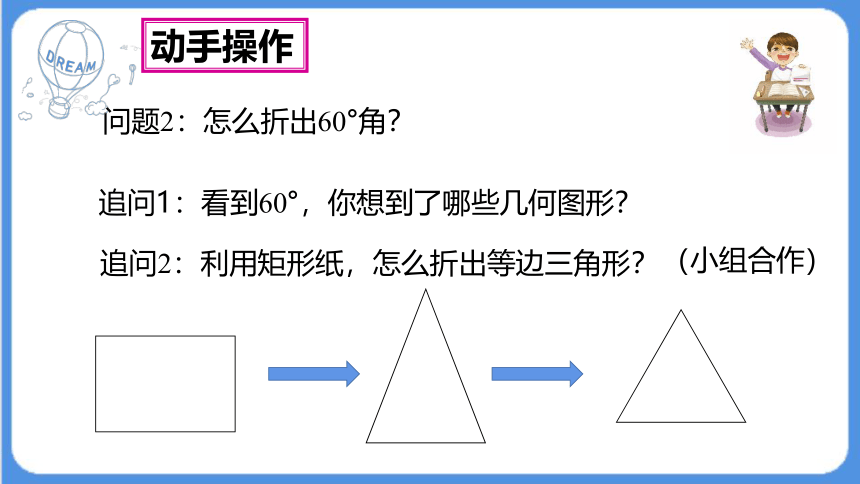
问题2:怎么折出60°角?
追问1:看到60°,你想到了哪些几何图形?
追问2:利用矩形纸,怎么折出等边三角形?
(小组合作)
动手操作
动手操作
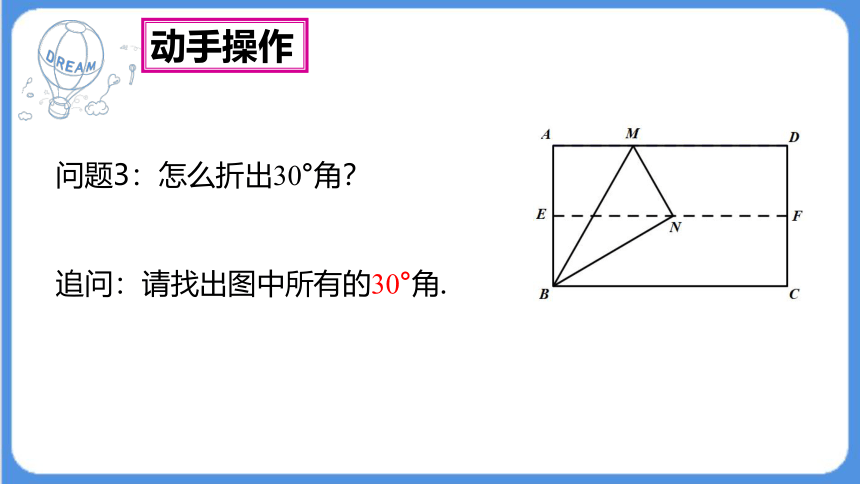
问题3:怎么折出30°角?
追问:请找出图中所有的30°角.
动手操作
问题4:怎么证明你折出的角是30°?
理论验证
已知:将矩形ABCD沿EF对折,折叠AB使点A落在折痕EF上,并使折痕经过点B,得到折痕BM.同时,得到了线段BN.
求证:∠ABM=∠MBN=∠NBC=30°.
理论验证
探究实质
证明:连接AN.
沿EF对折,可知:EF垂直平分AB.
∵点N在线段EF上,
∴AN=BN.
沿BM对折,可知: AB=BN,∠1=∠2.
∴ AB=BN=AN.
∴ ABN是等边三角形.
∴∠ABN=60°.
∴∠3=30°,∠1=∠2=30°.
即∠ABM=∠MBN=∠NMC=30°.
证明提高
问题5:怎么折出15°角呢?
追问:120°,150°角呢?
动手操作
对折可以平分一个角,还可以把一个角分成 等份,利用角的倍分关系或组合,容易折出:
头脑风暴
问题6:请找出尽可能多的60°角。
问题7:你能找到几个等边三角形?
问题8:四边形MBGH是什么图形?
问题9:还能折出哪些几何图形?
(2022年)23.(10分)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD , 使AD与BC重合,得到折痕EF, 把纸片展平;
操作二:在AD上选一点P , 沿BP折叠,使点A落在矩形内部点M 处,把纸片展平,连接PM,BM.
根据以上操作,当点M 在EF 上时,写出图1中一个30°的角: .
中考链接
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM 交CD 于点Q ,连接BQ.
①如图2,当点M 在EF上时,∠MBQ= °,∠CBQ= °;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ 与∠CBQ 的数量关系,并说明理由.
中考链接
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm, 当FQ=1cm时,直接写出AP 的长.
中考链接
(1)利用矩形纸片,你能折出哪些特殊角、哪些特殊图形?
(2)在探索和证明的过程中,用了哪些知识?
体现了哪些数学思想?
课堂小结
折纸与高科技
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学.
——华罗庚
教师寄语
1.必做题:通过折叠,自己制作一副三角尺.
2.选做题:上网查阅折30°角的更多方法,并思考其中的数学道理.
3.拓展题:在矩形ABCD中,AB=5,AD=8,E是AD上的一个动点,把 ABE沿着BE折叠,当点A的对应点N落在矩形ABCD的对称轴上时,求折痕BE的长.
布置作业
版本学科:人教版·初中数学·八年级下册
授课题目:《第十八章 数学活动——
折纸做60°,30°,15°的角》
创设情境
折纸艺术
人教版·初中数学·八年级下册
第十八章 数学活动
——折纸做60°,30°,15°的角
不用任何作图工具,利用矩形纸,怎么折出45°角?
对折可以平分一个角
动手操作
问题1:怎么折出60°,30°,15°角呢?
追问1:请观察这三个角,它们有什么关系?
追问2:只要找到哪个角,就可以得到其他两个角?
60°
30°
15°
60°,30°,15°
动手操作
问题2:怎么折出60°角?
追问1:看到60°,你想到了哪些几何图形?
追问2:利用矩形纸,怎么折出等边三角形?
(小组合作)
动手操作
动手操作
问题3:怎么折出30°角?
追问:请找出图中所有的30°角.
动手操作
问题4:怎么证明你折出的角是30°?
理论验证
已知:将矩形ABCD沿EF对折,折叠AB使点A落在折痕EF上,并使折痕经过点B,得到折痕BM.同时,得到了线段BN.
求证:∠ABM=∠MBN=∠NBC=30°.
理论验证
探究实质
证明:连接AN.
沿EF对折,可知:EF垂直平分AB.
∵点N在线段EF上,
∴AN=BN.
沿BM对折,可知: AB=BN,∠1=∠2.
∴ AB=BN=AN.
∴ ABN是等边三角形.
∴∠ABN=60°.
∴∠3=30°,∠1=∠2=30°.
即∠ABM=∠MBN=∠NMC=30°.
证明提高
问题5:怎么折出15°角呢?
追问:120°,150°角呢?
动手操作
对折可以平分一个角,还可以把一个角分成 等份,利用角的倍分关系或组合,容易折出:
头脑风暴
问题6:请找出尽可能多的60°角。
问题7:你能找到几个等边三角形?
问题8:四边形MBGH是什么图形?
问题9:还能折出哪些几何图形?
(2022年)23.(10分)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD , 使AD与BC重合,得到折痕EF, 把纸片展平;
操作二:在AD上选一点P , 沿BP折叠,使点A落在矩形内部点M 处,把纸片展平,连接PM,BM.
根据以上操作,当点M 在EF 上时,写出图1中一个30°的角: .
中考链接
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM 交CD 于点Q ,连接BQ.
①如图2,当点M 在EF上时,∠MBQ= °,∠CBQ= °;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ 与∠CBQ 的数量关系,并说明理由.
中考链接
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm, 当FQ=1cm时,直接写出AP 的长.
中考链接
(1)利用矩形纸片,你能折出哪些特殊角、哪些特殊图形?
(2)在探索和证明的过程中,用了哪些知识?
体现了哪些数学思想?
课堂小结
折纸与高科技
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学.
——华罗庚
教师寄语
1.必做题:通过折叠,自己制作一副三角尺.
2.选做题:上网查阅折30°角的更多方法,并思考其中的数学道理.
3.拓展题:在矩形ABCD中,AB=5,AD=8,E是AD上的一个动点,把 ABE沿着BE折叠,当点A的对应点N落在矩形ABCD的对称轴上时,求折痕BE的长.
布置作业
