人教版九年级上册23.1 图形的旋转 课件(共20张PPT)
文档属性
| 名称 | 人教版九年级上册23.1 图形的旋转 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
1
九年级-上册-第二十三章第1节
23.1 图形的旋转
旋转的性质
1.掌握旋转的基本性质.
2.能够根据旋转的基本性质解决实际问题.
目录
CONTENTS
2
B'
A'
C'
A
B
C
O
导入
△ABC是如何运动到△A′B′C的位置?
115°
旋转中心是点__________;
图中对应点有_______________________________________;
图中对应线段有_____________________________________.
每对对应线段的长度有怎样的关系?
图中旋转角等于______.
O
点A与点A′,点B与点B′,点C与点C′
线段CA与C'A′、CB与C'B′、AB与A′B′
115°
相等
根据上图填空.
知识讲解
难点突破
A
D
E
B
F
C
O
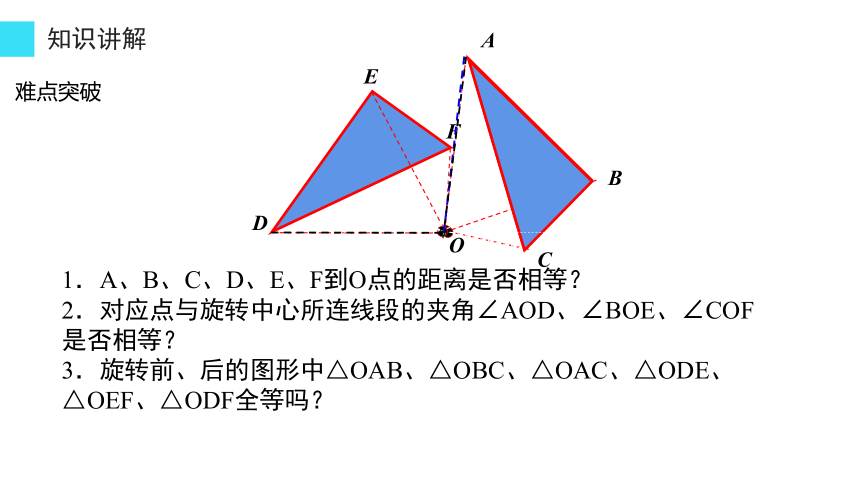
1.A、B、C、D、E、F到O点的距离是否相等?
2.对应点与旋转中心所连线段的夹角∠AOD、∠BOE、∠COF是否相等?
3.旋转前、后的图形中△OAB、△OBC、△OAC、△ODE、△OEF、△ODF全等吗?
知识讲解
难点突破
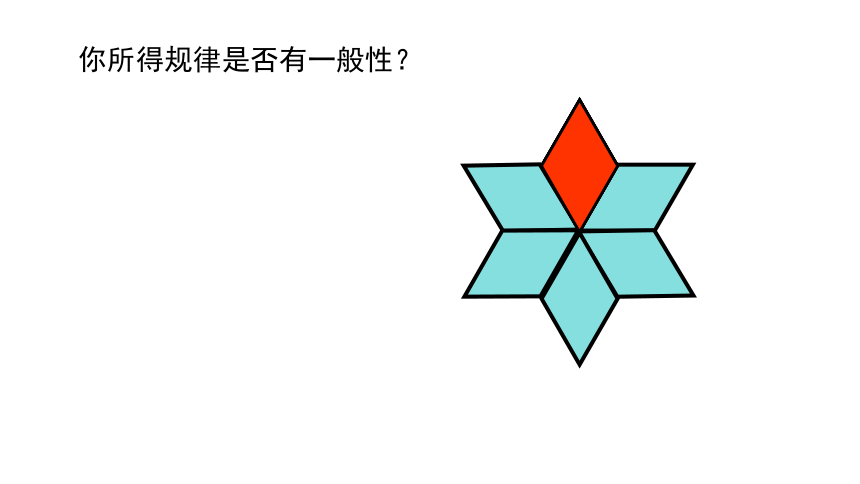
你所得规律是否有一般性?
D
E
A
B
F
C
O
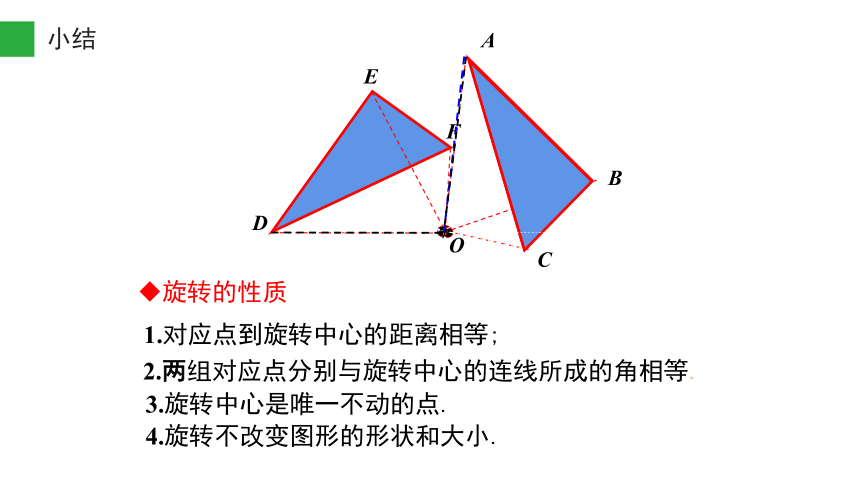
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心的连线所成的角相等.
旋转的性质
3.旋转中心是唯一不动的点.
4.旋转不改变图形的形状和大小.
小结
5.△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( )
A.DE=3
B.AE=4
C.∠CAB是旋转角
D.∠CAE是旋转角
D
难点巩固
课堂练习
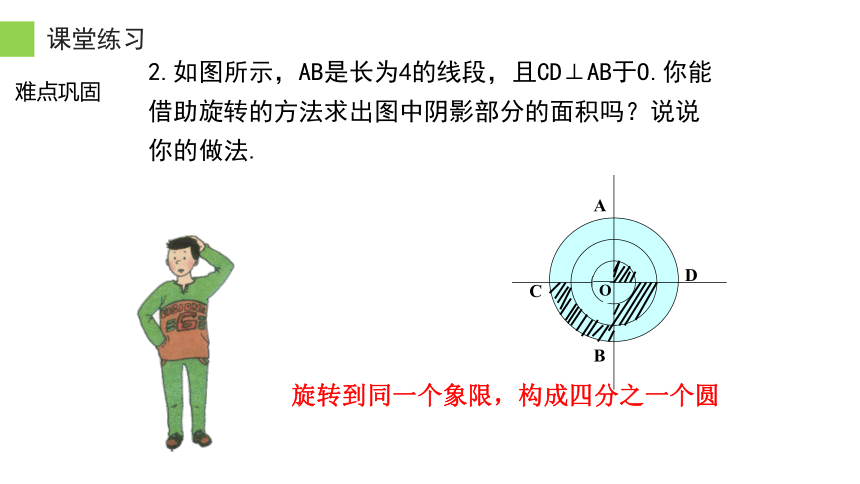
2.如图所示,AB是长为4的线段,且CD⊥AB于O.你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法.
O
A
B
C
D
旋转到同一个象限,构成四分之一个圆
难点巩固
课堂练习
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
旋转全等三角形
11
旋转全等三角形的推理证明,利用旋转的思想构造全等三角形解决数学问题。
A
B
B′
A′
C
.
M′
M
.
.
.
.
导入
旋转的性质:
(1)旋转过程中对应点到旋转中心的距离相等。
(2)旋转过程中对应点与旋转中心所连线段的夹角都等于旋转角。
(3)旋转前后的图形是全等形。
旋转全等
旋转全等三角形
旋转
三角形
A
C
B
C'
B'
B'
C'
13
A
B
C
旋转全等三角形
导入
A
C
B
C'
B'
14
B'
C'
A
B
C
知识讲解
难点突破
旋转全等三角形的性质:
连接全等三角形三角形的对应顶点,会形成两个顶角相同,顶角顶点重合的等腰三角形。
15
知识讲解
难点突破
A
B
B'
C
C'
A
B'
B
C'
C
旋转全等三角形性质的逆应用: 顶角相等且共顶角顶点的两个等腰三角形可以形成旋转全等三角形。
知识讲解
推理证明
如图:在△ABB'中,AB=AB',在△ACC'中,AC=AC',且∠B'AB=∠C'AC.
证明:△ABC≌△AB'C'.
证明:
在△ABC与△AB'C'中
AB=AB'
∠B'AC'=∠BAC
AC=AC'
∵∠B'AB=∠C'AC
∴∠B'AB+∠BAC'=∠C'AC+∠BAC'
∴∠B'AC'=∠BAC
∴△ABC≌△AB'C'(SAS)
证明:
在△DAC与△EAB中
AD=AE
∠DAC=∠EAB
AC=AB
∴AD=AE,AC=AB
∠DAE=∠CAB=90°
∴∠DAE+∠EAC=∠CAB+∠EAC
∴∠DAC=∠EAB
∴△DAC≌△EAB(SAS)
∴BE=DC(全等三角形的对应边相等)
∵△ABC与△ADE都是等腰直角三角形
课堂练习
B
E
D
A
C
练习1:△ABC与△ADE都是等腰直角三角形,分别连接BE与DC。
证明:BE=DC。
难点巩固
课堂练习
18
难点巩固
变式:△ABC与△ADE都是等腰直角三角形。请问BE与DC有什么关系?
B
E
D
A
C
解:
在△DAC与△EAB中
AD=AE
∠DAC=∠EAB
AC=AB
∴∠DAE-∠CAE=∠CAB-∠CAE
∴∠DAC=∠EAB
∴△DAC≌△EAB(SAS)
∴BE=DC(全等三角形的对应边相等)
∴∠DCA=∠EBA(全等三角形的对应角相等)
∵△ABC与△ADE都是等腰直角三角形
∴AD=AE,AC=AB
∠DAE=∠CAB=90°
F
延长BE交DC与点F,交AC于点G.
G
在△DGC中,
∠FGC+∠DCA+∠GFC=180°
∴∠GFC=90°
即BE⊥DC。
BE=DC,BE⊥DC
在Rt△GAB中,∠EBA+∠AGB=90°
又∵∠FGC=∠EGA(对顶角相等)
∴∠FGC+∠DCA=90°(等量代换)
小结
(1)连接旋转全等三角形对应顶点,会出现两个顶角相同,顶角顶点重合的等腰三角形。
(2)如果有两个顶角顶点重合的等腰三角形,我们就可以得出两个全等三角形。共顶点顶角,顶角相等的等腰三角形是旋转全等的标志。
习题中常见的两类图形:1、旋转前后的图形已经给出;2、只有旋转前的图形,需要自己动手作辅助线构造出旋转后的图形。
19
A
B
B'
C
C'
A
B'
B
C'
C
谢谢聆听
1
九年级-上册-第二十三章第1节
23.1 图形的旋转
旋转的性质
1.掌握旋转的基本性质.
2.能够根据旋转的基本性质解决实际问题.
目录
CONTENTS
2
B'
A'
C'
A
B
C
O
导入
△ABC是如何运动到△A′B′C的位置?
115°
旋转中心是点__________;
图中对应点有_______________________________________;
图中对应线段有_____________________________________.
每对对应线段的长度有怎样的关系?
图中旋转角等于______.
O
点A与点A′,点B与点B′,点C与点C′
线段CA与C'A′、CB与C'B′、AB与A′B′
115°
相等
根据上图填空.
知识讲解
难点突破
A
D
E
B
F
C
O
1.A、B、C、D、E、F到O点的距离是否相等?
2.对应点与旋转中心所连线段的夹角∠AOD、∠BOE、∠COF是否相等?
3.旋转前、后的图形中△OAB、△OBC、△OAC、△ODE、△OEF、△ODF全等吗?
知识讲解
难点突破
你所得规律是否有一般性?
D
E
A
B
F
C
O
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心的连线所成的角相等.
旋转的性质
3.旋转中心是唯一不动的点.
4.旋转不改变图形的形状和大小.
小结
5.△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( )
A.DE=3
B.AE=4
C.∠CAB是旋转角
D.∠CAE是旋转角
D
难点巩固
课堂练习
2.如图所示,AB是长为4的线段,且CD⊥AB于O.你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法.
O
A
B
C
D
旋转到同一个象限,构成四分之一个圆
难点巩固
课堂练习
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
旋转全等三角形
11
旋转全等三角形的推理证明,利用旋转的思想构造全等三角形解决数学问题。
A
B
B′
A′
C
.
M′
M
.
.
.
.
导入
旋转的性质:
(1)旋转过程中对应点到旋转中心的距离相等。
(2)旋转过程中对应点与旋转中心所连线段的夹角都等于旋转角。
(3)旋转前后的图形是全等形。
旋转全等
旋转全等三角形
旋转
三角形
A
C
B
C'
B'
B'
C'
13
A
B
C
旋转全等三角形
导入
A
C
B
C'
B'
14
B'
C'
A
B
C
知识讲解
难点突破
旋转全等三角形的性质:
连接全等三角形三角形的对应顶点,会形成两个顶角相同,顶角顶点重合的等腰三角形。
15
知识讲解
难点突破
A
B
B'
C
C'
A
B'
B
C'
C
旋转全等三角形性质的逆应用: 顶角相等且共顶角顶点的两个等腰三角形可以形成旋转全等三角形。
知识讲解
推理证明
如图:在△ABB'中,AB=AB',在△ACC'中,AC=AC',且∠B'AB=∠C'AC.
证明:△ABC≌△AB'C'.
证明:
在△ABC与△AB'C'中
AB=AB'
∠B'AC'=∠BAC
AC=AC'
∵∠B'AB=∠C'AC
∴∠B'AB+∠BAC'=∠C'AC+∠BAC'
∴∠B'AC'=∠BAC
∴△ABC≌△AB'C'(SAS)
证明:
在△DAC与△EAB中
AD=AE
∠DAC=∠EAB
AC=AB
∴AD=AE,AC=AB
∠DAE=∠CAB=90°
∴∠DAE+∠EAC=∠CAB+∠EAC
∴∠DAC=∠EAB
∴△DAC≌△EAB(SAS)
∴BE=DC(全等三角形的对应边相等)
∵△ABC与△ADE都是等腰直角三角形
课堂练习
B
E
D
A
C
练习1:△ABC与△ADE都是等腰直角三角形,分别连接BE与DC。
证明:BE=DC。
难点巩固
课堂练习
18
难点巩固
变式:△ABC与△ADE都是等腰直角三角形。请问BE与DC有什么关系?
B
E
D
A
C
解:
在△DAC与△EAB中
AD=AE
∠DAC=∠EAB
AC=AB
∴∠DAE-∠CAE=∠CAB-∠CAE
∴∠DAC=∠EAB
∴△DAC≌△EAB(SAS)
∴BE=DC(全等三角形的对应边相等)
∴∠DCA=∠EBA(全等三角形的对应角相等)
∵△ABC与△ADE都是等腰直角三角形
∴AD=AE,AC=AB
∠DAE=∠CAB=90°
F
延长BE交DC与点F,交AC于点G.
G
在△DGC中,
∠FGC+∠DCA+∠GFC=180°
∴∠GFC=90°
即BE⊥DC。
BE=DC,BE⊥DC
在Rt△GAB中,∠EBA+∠AGB=90°
又∵∠FGC=∠EGA(对顶角相等)
∴∠FGC+∠DCA=90°(等量代换)
小结
(1)连接旋转全等三角形对应顶点,会出现两个顶角相同,顶角顶点重合的等腰三角形。
(2)如果有两个顶角顶点重合的等腰三角形,我们就可以得出两个全等三角形。共顶点顶角,顶角相等的等腰三角形是旋转全等的标志。
习题中常见的两类图形:1、旋转前后的图形已经给出;2、只有旋转前的图形,需要自己动手作辅助线构造出旋转后的图形。
19
A
B
B'
C
C'
A
B'
B
C'
C
谢谢聆听
同课章节目录
