分班考常考易错检测卷(试题) 小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 分班考常考易错检测卷(试题) 小学数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 10:10:01 | ||
图片预览



文档简介
分班考常考易错检测卷(试题)-小学数学六年级下册苏教版
一、口算和估算
1.直接写出得数。
二、脱式计算
2.计算下面各题,能简便计算的要用简便方法计算。
三、解方程或比例
3.解方程。
四、图形计算
4.计算下图长方形ABCD的面积。(单位:厘米)
五、选择题
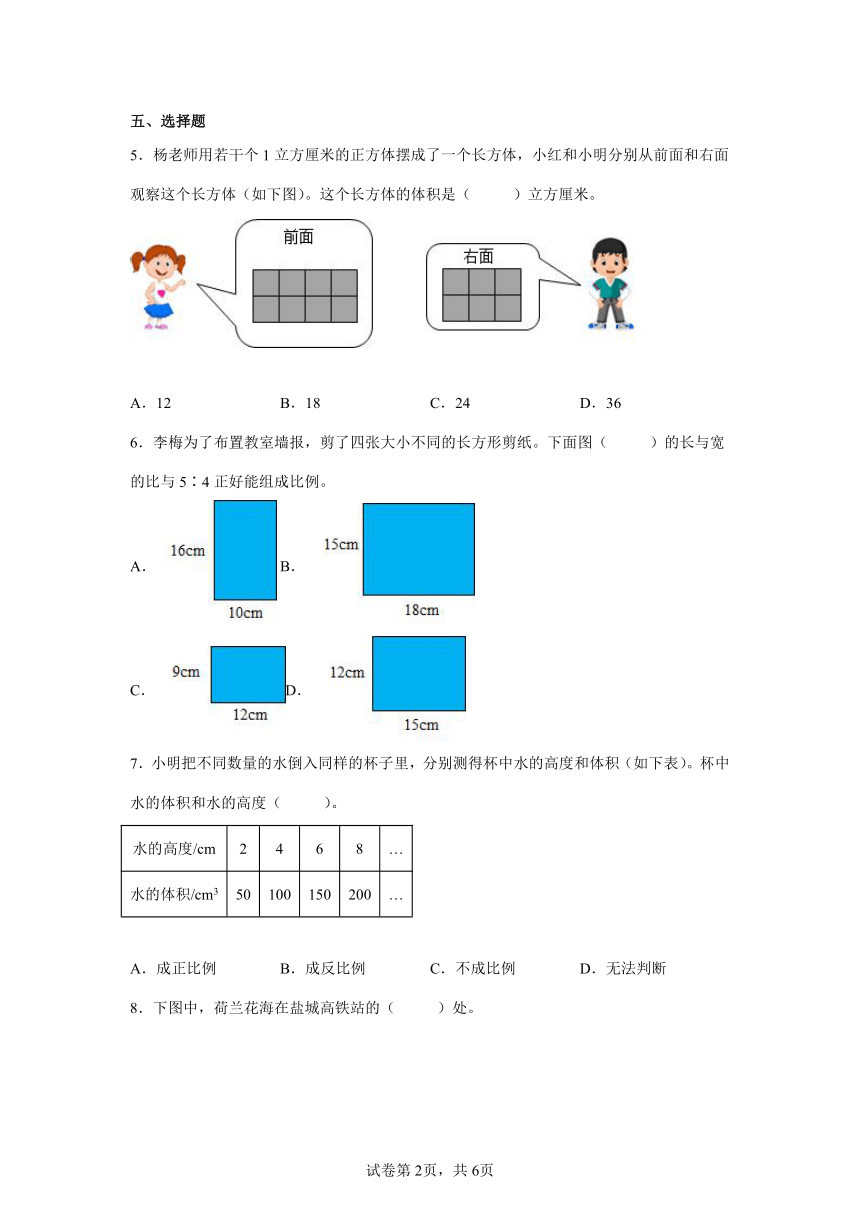
5.杨老师用若干个1立方厘米的正方体摆成了一个长方体,小红和小明分别从前面和右面观察这个长方体(如下图)。这个长方体的体积是( )立方厘米。
A.12 B.18 C.24 D.36
6.李梅为了布置教室墙报,剪了四张大小不同的长方形剪纸。下面图( )的长与宽的比与5∶4正好能组成比例。
A. B.
C.D.
7.小明把不同数量的水倒入同样的杯子里,分别测得杯中水的高度和体积(如下表)。杯中水的体积和水的高度( )。
水的高度/cm 2 4 6 8 …
水的体积/cm3 50 100 150 200 …
A.成正比例 B.成反比例 C.不成比例 D.无法判断
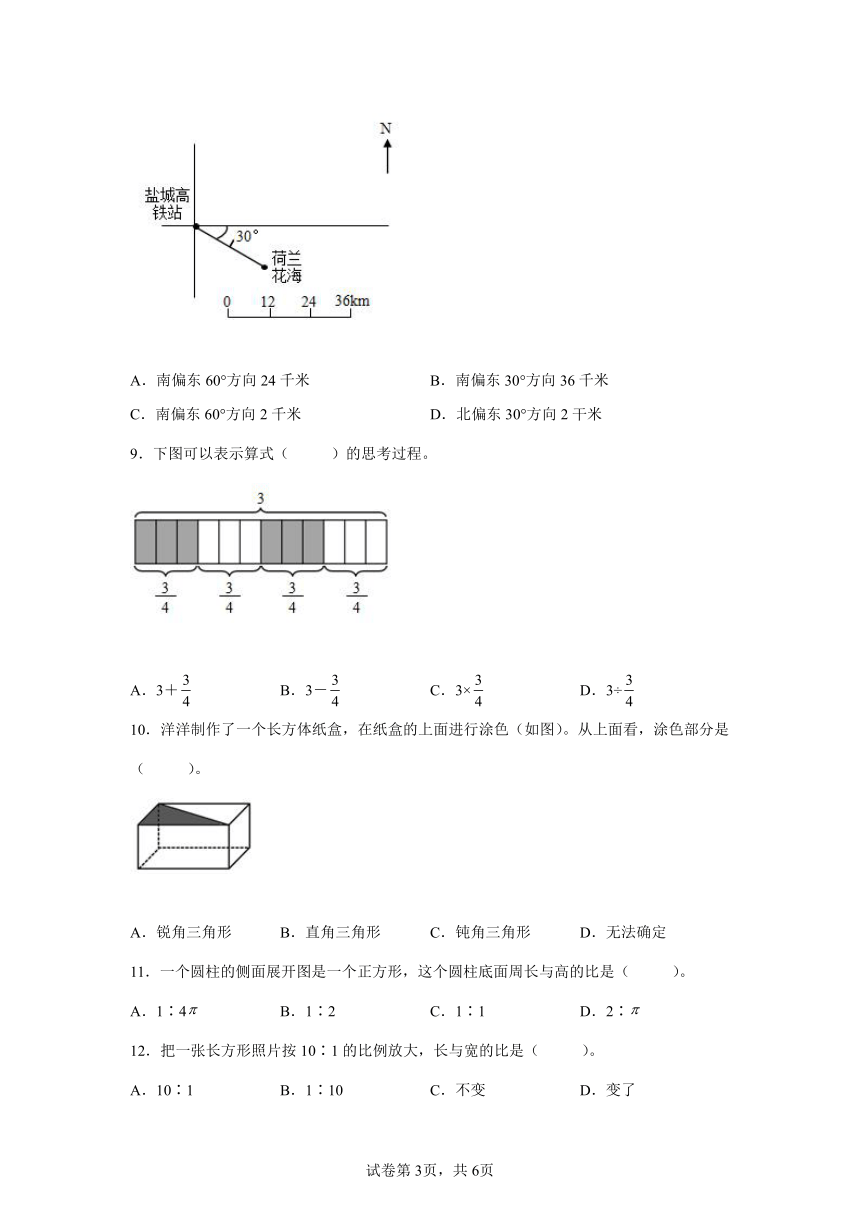
8.下图中,荷兰花海在盐城高铁站的( )处。
A.南偏东60°方向24千米 B.南偏东30°方向36千米
C.南偏东60°方向2千米 D.北偏东30°方向2干米
9.下图可以表示算式( )的思考过程。
A.3+ B.3- C.3× D.3÷
10.洋洋制作了一个长方体纸盒,在纸盒的上面进行涂色(如图)。从上面看,涂色部分是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
11.一个圆柱的侧面展开图是一个正方形,这个圆柱底面周长与高的比是( )。
A.1∶4 B.1∶2 C.1∶1 D.2∶
12.把一张长方形照片按10∶1的比例放大,长与宽的比是( )。
A.10∶1 B.1∶10 C.不变 D.变了
13.下图中圆柱的表面被涂上了一层红漆,若沿虚线切开后,没有红漆的面共有( )个。
A.8 B.12 C.24 D.36
14.一个圆柱体和一个圆锥体等底等高,它们的体积一共是60立方厘米,其中圆锥体的体积( )立方厘米.
A.15 B.20 C.40 D.45
六、填空题
15.美丽的油车水库占地面积约为3009704平方米,横线上的数读作________,省略“万”后面的尾数约是________万。
16.把一根5米长的铁丝剪成同样长的7段,第3段长 米,每段长度是1米的。
17.如果3A=1.8B(A、B均不为0),那么A与B成________比例;A与B的最简整数比是________。
18.一个圆锥形零件是由一个底面半径是5厘米、高是6厘米的圆柱形铁块铸造而成,这个零件的体积是________立方厘米;如果这个圆锥形零件的底面半径也是5厘米,那么它的高是________厘米。
19.王师傅加工一批零件。经查验,已经加工的零件中有72个合格,8个不合格,合格率是________。后来又加工了20个零件,经查验,全部合格,他加工的全部零件的合格率是________。
20.在4个同样的大盒和6个同样的小盒里装满同样的球,正好是302个。如果每个大盒比小盒多装8个,那么每个大盒装( )个球,每个小盒装( )个球。
21.一个表面涂满红漆的圆柱形木块,底面直径是2厘米,高是9厘米。若沿虚线(如图)切开后得到一些完全一样的小木块,这些小木块的表面积之和比原来圆柱的表面积增加了________平方厘米,没有涂红漆的面共有________个。
22.学校兴趣小组添置了一些足球和篮球。如果篮球个数不变,把足球个数增加,两种球的总数将达到147个,把篮球个数减少,两种球的总数是115个。学校兴趣小组添置的足球有________个,篮球有________个。
七、解答题
23.一双运动鞋打7折出售,比原来便宜25.5元. 这双运动鞋的原价是多少元?
24.果园里桃树的棵数相当于梨树棵数的,相当于苹果树棵数的.如果梨树比苹果树少180棵,这个果园里桃树、梨树、苹果树各多少棵?
25.一个圆锥形黄沙,底面直径是4米,高是1.5米,按每立方米黄沙重1.7吨计算,这堆黄沙大约重多少吨?(π取值为3)
26.一个长方体棱长总和是220厘米,长和宽的比是2∶1,宽与高的比是3∶2,这个长方体的体积是多少立方厘米?
27.一个高4.8分米的铁皮油桶,底面是边长2.5分米的正方形(铁皮的厚度忽略不计)。把这样的一桶油注入容积是1.25升的瓶子里,需要装多少瓶?
28.春季植树活动中,长征小学的五年级学生比六年级学生少植树126棵,六年级学生植树的棵数是五年级学生的1.5倍,长征小学五、六年级学生各植树多少棵?(列方程解答)
29.一本书科技书,夏小轩同学第一天看了它的,第二天看了它的20%,这时两天一共看了135页。
(1)这本书一共有多少页?
(2)剩下的页数他计划3天看完,平均每天要看多少页?
30.甲、乙、丙三人一起参加长跑比赛,当甲跑完全程的75%时,乙才到达全程的处。这时,丙恰好跑到甲、乙两人之间的中点处,并且离终点还有875米。求这次长跑的全程是多少米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.27;130;;
0.6;;;
【详解】略
2.4100;;
1;;
【分析】4260-3840÷24,先计算除法,再计算减法;
×(1-),先计算括号里的减法,再计算乘法;
,先计算括号里的减法和加法,再计算除法;
+-(+),根据减法性质,原式化为:+--,再根据加法交换律和结合律,原式化为:(-)+(-),再进行计算;
,把除法换成乘法,原式化为:×+×,再根据乘法分配律,原式化为:×(+),再进行计算;
,先计算小括号里的减法,再计算中括号里的乘,最后计算括号外的除法。
【详解】4260-3840÷24
=4260-160
=4100
×(1-)
=×
=
=(-)÷(+)
=÷
=×
=
=
=+--
=(-)+(-)
=+
=1
=×+×
=×(+)
=×(+)
=×
=
=÷[(-)×]
=÷[×]
=÷
=×
=
3.;;
【分析】根据等式的性质,方程两边同时减5.4,再同时除以2.5;
原方程化简后得,根据等式的性质,方程两边同时除以;
根据比例的性质将原式化成方程得,根据等式的性质,方程两边同时除以0.6。
【详解】
解:
解:
解:
4.270平方厘米
【分析】如下图:
连接BE,三角形BCE的面积为:18×15÷2=135(平方厘米),而三角形BCE的面积也可以是:BC×BC边上的高÷2,BC边上的高则与CD或AB相等,从这一点可分析出长方形ABCD的面积是三角形BCE的面积的2倍,据此解答。
【详解】18×15÷2×2
=270÷2×2
=270(平方厘米)
5.C
【分析】根据从前面、右面观察到的形状可知:该长方体的长是4厘米、宽是3厘米、高是2厘米,带入长方体的体积公式计算即可。
【详解】4×3×2
=12×2
=24(立方厘米)
故答案为:C
【点睛】明确长方体的长、宽、高是解题的关键。
6.D
【分析】先求出5∶4的比值,再求出各选项图形中长与宽的比值,与5∶4的比值比较,如果相等就能组成比例;据此解答即可。
【详解】5∶4=5÷4=
A.16∶10=16÷10=,≠,所以与5∶4不能组成比例;
B.18∶15=18÷15=,≠,所以与5∶4不能组成比例;
C.12∶9=12÷9=,≠,所以与5∶4不能组成比例;
D.15∶12=15÷12=,=,所以与5∶4能组成比例。
故答案为:D
【点睛】此题考查比例意义的运用,明确比例是表示两个比相等的式子。
7.A
【分析】判断水的体积和水的高度之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;比值、乘积均不一定则不成比例;据此解答。
【详解】50∶2=50÷2=25
100∶4=100÷4=25
150∶6=150÷6=25
200∶8=200÷8=25
杯中水的体积和水的高度的比值一定,所以杯中水的体积和水的高度成正比例。
故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
8.A
【分析】根据“上北下南,左西右东”确定方向,注意观测点是盐城高铁站。再根据图上距离和比例尺的关系确定实际距离。
【详解】12×2=24(千米)
90°-30°=60°
荷兰花海在盐城高铁站的东偏南30°方向24千米处或南偏东60°方向24千米处。
故答案为:A
【点睛】本题主要考查图上距离与实际距离、比例尺的关系。
9.D
【分析】由图可知:图中表示3中包含几个,符合除法的意义。
【详解】图中表示3中包含几个,用算式表示是3÷。
故答案为:D
【点睛】本题主要考查分数除法的意义。
10.B
【分析】根据图形可知,涂色部分是长方体的一个面,有一个角是直角,所以从上面看,涂色部分是直角三角形,据此解答。
【详解】根据分析可知,洋洋制作了一个长方体纸盒,在纸盒的上面进行涂色(如图)。从上面看,涂色部分是直角三角形。
故答案为:B
【点睛】解答本题的关键是明确长方体的特征。根据三角形的分类和认识知识进行解答。
11.C
【分析】圆柱的侧面展开图是一个正方形,说明圆柱的底面周长=高,据此写出两者的比即可。
【详解】如果一个圆柱的侧面展开图是一个正方形,那么该圆柱的高和底面周长的比是1∶1。
故答案为:C
【点睛】本题考查了圆柱的展开图及比的意义,圆柱侧面沿高展开一般是长方形,当底面周长=高时,侧面沿高展开就是正方形。
12.C
【详解】设原来的长与宽的比是a∶b,
放大后的比为(a×10)∶(b×10)=a∶b;
故答案为:C。
13.C
【分析】没有红漆的面应是每次的切面,圆柱被竖着切了2刀,横着切了1刀,每切一刀都要增加8个面,所以共有8×3=24个面没有红漆,据此解答。
【详解】根据分析可得,
8×3=24(个)
所以没有红漆的面共有24个。
故答案为:C
【点睛】此题主要考查立体图形的切拼,重点理解每切一刀都要增加8个没有红漆的面。
14.A
【详解】略
15. 三百万九千七百零四 301
【分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零,即可读出此数;省略“万”后面的尾数就是四舍五入到万位,就是把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字。
【详解】3009704读作:三百万九千七百零四;3009704≈301万。
【点睛】本题主要考查整数的读法和求近似数,注意:分级读即可快速、正确地读出此数;求近似数时要带计数单位。
16.;
【分析】把一根5米长的铁丝剪成同样长的7段,求第3段的长度,用这根铁丝的长度除以剪成的段数(与段的序数无关);求每段长是1米的几分之几,用每段的长度除以1米,据此解答。
【详解】5÷7=(米)
÷1=
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称。
17. 正 3∶5
【分析】先把等积式化为比例式,再根据判断两种相关联的量成什么比例,就看两种相关量中相对应的两个数是商一定还是积一定,如果商一定,就成正比例;如果积一定,就成反比例来判断即可;把等积式化为比例式,再根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外)比值不变,进而把比化成最简比。
【详解】因为3A=1.8B(A、B均不为0),即:A÷B=0.6(一定),所以成正比例。
A∶B=1.8∶3
=(1.8÷0.6)∶(3÷0.6)
=3∶5
【点睛】本题主要考查了化简比及辨识成正比例的量与成反比例的量,解题的关键是把等积式化为比例式。
18. 471 18
【分析】根据圆柱的体积=底面积×高,圆锥的体积=底面积×高÷3,则高=圆锥的体积×3÷底面积,解答此题即可。
【详解】3.14×5×5×6
=15.7×30
=471(立方厘米)
471×3÷(3.14×5×5)
=1413÷78.5
=18(厘米)
【点睛】熟练掌握圆锥和圆柱的体积公式,是解答此题的关键。
19. 90% 92%
【分析】合格率是指合格的零件的个数占全部零件的个数的百分之几,先用“72+8”求出这批零件的总个数,然后根据公式:合格率=合格零件数÷加工的全部零件个数×100%,进行解答即可;求他加工的全部零件的合格率,先求出加工的全部的零件个数与合格零件的总个数,然后根据:合格率=合格零件数÷加工的全部零件个数×100%,进行解答即可。
【详解】72÷(72+8)×100%
=72÷80×100%
=90%
(72+20)÷(72+20+8)×100%
=92÷100×100%
=92%
【点睛】此题属于百分率问题,掌握合格率的表达式是解题的关键。
20. 35 27
【分析】此题考查学生用假设法解决问题。如果假设10个均为小盒,则要将每个大盒中多装的8个球去掉。如果假设10个均为大盒,则要将每个小盒中少掉的8个球加上。
【详解】假设10个均为小盒
302-4×8=270(个)
270÷10=27(个)
大盒装球个数:27+8=35(个)。
21. 84.56 40
【分析】根据图示可知,把圆柱沿高截成3段,表面积增加2×2=4个底面积,沿底面直径切成4块,表面积增加(2×4)个半径乘高;没有涂色的面即这些切面,是切完之后露出来的面,即(4×2×2)个圆和(2×4×3)个长方形的面。
【详解】3.14×(2÷2)2×(2×2)+(2×4)×(2÷2)×9
=3.14×4+72
=84.56(平方厘米)
4×2×2+2×4×3
=16+24
=40(个)
【点睛】本题的考查圆柱的切割问题,要求同学展开空间想象能力。
22. 76 52
【分析】由题意可知,原足球个数×+原篮球个数×=147-115,根据乘法分配律可得(原足球个数+原篮球个数)×=147-115。根据分数除法的意义,用(147-115)除以即可求出原来足球、篮球的总个数。原来两球的总个数与147个之差就是增加足球的个数,原来两球的总个数与115个之差就是增加篮球的个数。分别用两种球增加的个数除以即可求出它们各自添置的个数。
【详解】(147-115)÷
=32÷
=128(个)
147-128=19(个)
足球:19÷=76(个)
128-115=13(个)
篮球:13÷=52(个)
【点睛】解答此题的关键和难点是:明白147个与115个之差是原来两种球总个数的,然后根据分数除法的意义求出原来两种球的总个数。
23.85元
【详解】,
=25.5÷30%,
=85(元);
答:这双运动鞋的原价是85元.
【点睛】打七折是指现价是原价的70%,把原价看成单位“1”,现价比原价便宜了(1-70%),它对应的数量是25.5元,求原价用除法.
24.桃树:180÷(7-5)×3=270(棵)
梨树:270÷=450(棵)
苹果树:270÷=630(棵)
【详解】略
25.10.2吨
【分析】圆锥的体积公式为:V=Sh,在此题中,先根据底面直径是4米,进而求出底面半径,然后根据圆的面积公式求出底面积,再根据圆锥的体积公式求出圆锥的体积,最后根据“黄沙的体积×每立方米沙的重量=这堆沙的总重量”解答即可。
【详解】×3×(4÷2)2×1.5×1.7
=1×22×1.5×1.7
=4×1.5×1.7
=10.2(吨)
答:这堆黄沙大约重10.2吨。
【点睛】此题考查了圆锥体积的求解方法,要注意不要忘记乘。
26.4500立方厘米
【分析】根据长方体的棱长总和是220厘米,先求出长、宽、高的和是220÷4=55厘米,再根据长宽高的比,即可分别求出长方体的长宽高的值,利用长方体的体积公式:V=abh,代入求解即可。
【详解】长和宽的比是2∶1,可得长和宽的比是6∶3,
所以长、宽、高的比是6∶3∶2;
220÷4÷(6+3+2)
=55÷11
=5(厘米)
5×6=30(厘米)
5×3=15(厘米)
5×2=10(厘米)
30×15×10=4500(立方厘米)
答:这个长方体的体积是4500立方厘米。
【点睛】此题考查了长方体的棱长总和和长方体的体积公式的运用以及比的应用。
27.24瓶
【分析】先根据长方体的体积公式求出这样一桶油的体积是:2.5×2.5×4.8=30立方分米=30升,根据除法的意义,计算出里面有多少个1.25升,就可以装几瓶。
【详解】2.5×2.5×4.8÷1.25
=30÷1.25
=24(瓶)
答:需要装24瓶。
【点睛】此题考查长方体体积公式的计算和除法意义的灵活应用。
28.五年级252棵,六年级378棵。
【分析】根据题意可得等量关系式:五年级学生植树的棵数×1.5 =六年级学生植树的棵数,五年级学生植树的棵数+126=六年级学生植树的棵数,设五年级学生植树x棵,然后列方程解答即可。
【详解】解:设五年级学生植树x棵。
1.5x=x+126
1.5x-x=x+126-x
0.5x=126
0.5x÷0.5=126÷0.5
x=252
252×1.5=378(棵)
答:长征小学五年级学生植树252棵,六年级学生植树378棵。
【点睛】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
29.(1)300页;
(2)55页
【分析】(1)第一天看了全书总页数的,第二天看了全书总页数的20%,根据分数加法的意义,两天共看了总页数的(+20%),又知道两天一共看了135页,根据分数除法的意义,用所看页数除以其占总页数的分率,即得共有多少页;
(2)依据剩下的页数=总共的-已经看了的,求出剩下的页数,用剩下的页数除以3即可求解。
【详解】(1)135÷(+20%)
=135÷0.45
=300(页)
答:这本书一共有300页。
(300-135)÷3
=165÷3
=55(页)
答:平均每天要看55页。
【点睛】解答分数应用题的关键是找出题目中的单位“1”,再根据单位“1”的已知和未知情况,确定解答方法。
30.3000米
【分析】设全程为单位“1”,因为丙恰好跑到甲、乙两人之间的中点处,可知丙此时到达全程的(75%-)×,再加上全程剩下的(1-75%),即为875米所对应的分率,根据分数除法的意义,用除法可解答此题。
【详解】(75%-)×+(1-75%)
=(-)×+(1-)
=×+
=
875÷=3000(米)
答:这次长跑的全程是3000米。
【点睛】解答此题的关键是要找准875米所对应的分率,再用分数除法的意义去求全程。提示:如果觉得题目难以理解,也可以画线段图帮助理解题意。
答案第1页,共2页
答案第1页,共2页
一、口算和估算
1.直接写出得数。
二、脱式计算
2.计算下面各题,能简便计算的要用简便方法计算。
三、解方程或比例
3.解方程。
四、图形计算
4.计算下图长方形ABCD的面积。(单位:厘米)
五、选择题
5.杨老师用若干个1立方厘米的正方体摆成了一个长方体,小红和小明分别从前面和右面观察这个长方体(如下图)。这个长方体的体积是( )立方厘米。
A.12 B.18 C.24 D.36
6.李梅为了布置教室墙报,剪了四张大小不同的长方形剪纸。下面图( )的长与宽的比与5∶4正好能组成比例。
A. B.
C.D.
7.小明把不同数量的水倒入同样的杯子里,分别测得杯中水的高度和体积(如下表)。杯中水的体积和水的高度( )。
水的高度/cm 2 4 6 8 …
水的体积/cm3 50 100 150 200 …
A.成正比例 B.成反比例 C.不成比例 D.无法判断
8.下图中,荷兰花海在盐城高铁站的( )处。
A.南偏东60°方向24千米 B.南偏东30°方向36千米
C.南偏东60°方向2千米 D.北偏东30°方向2干米
9.下图可以表示算式( )的思考过程。
A.3+ B.3- C.3× D.3÷
10.洋洋制作了一个长方体纸盒,在纸盒的上面进行涂色(如图)。从上面看,涂色部分是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
11.一个圆柱的侧面展开图是一个正方形,这个圆柱底面周长与高的比是( )。
A.1∶4 B.1∶2 C.1∶1 D.2∶
12.把一张长方形照片按10∶1的比例放大,长与宽的比是( )。
A.10∶1 B.1∶10 C.不变 D.变了
13.下图中圆柱的表面被涂上了一层红漆,若沿虚线切开后,没有红漆的面共有( )个。
A.8 B.12 C.24 D.36
14.一个圆柱体和一个圆锥体等底等高,它们的体积一共是60立方厘米,其中圆锥体的体积( )立方厘米.
A.15 B.20 C.40 D.45
六、填空题
15.美丽的油车水库占地面积约为3009704平方米,横线上的数读作________,省略“万”后面的尾数约是________万。
16.把一根5米长的铁丝剪成同样长的7段,第3段长 米,每段长度是1米的。
17.如果3A=1.8B(A、B均不为0),那么A与B成________比例;A与B的最简整数比是________。
18.一个圆锥形零件是由一个底面半径是5厘米、高是6厘米的圆柱形铁块铸造而成,这个零件的体积是________立方厘米;如果这个圆锥形零件的底面半径也是5厘米,那么它的高是________厘米。
19.王师傅加工一批零件。经查验,已经加工的零件中有72个合格,8个不合格,合格率是________。后来又加工了20个零件,经查验,全部合格,他加工的全部零件的合格率是________。
20.在4个同样的大盒和6个同样的小盒里装满同样的球,正好是302个。如果每个大盒比小盒多装8个,那么每个大盒装( )个球,每个小盒装( )个球。
21.一个表面涂满红漆的圆柱形木块,底面直径是2厘米,高是9厘米。若沿虚线(如图)切开后得到一些完全一样的小木块,这些小木块的表面积之和比原来圆柱的表面积增加了________平方厘米,没有涂红漆的面共有________个。
22.学校兴趣小组添置了一些足球和篮球。如果篮球个数不变,把足球个数增加,两种球的总数将达到147个,把篮球个数减少,两种球的总数是115个。学校兴趣小组添置的足球有________个,篮球有________个。
七、解答题
23.一双运动鞋打7折出售,比原来便宜25.5元. 这双运动鞋的原价是多少元?
24.果园里桃树的棵数相当于梨树棵数的,相当于苹果树棵数的.如果梨树比苹果树少180棵,这个果园里桃树、梨树、苹果树各多少棵?
25.一个圆锥形黄沙,底面直径是4米,高是1.5米,按每立方米黄沙重1.7吨计算,这堆黄沙大约重多少吨?(π取值为3)
26.一个长方体棱长总和是220厘米,长和宽的比是2∶1,宽与高的比是3∶2,这个长方体的体积是多少立方厘米?
27.一个高4.8分米的铁皮油桶,底面是边长2.5分米的正方形(铁皮的厚度忽略不计)。把这样的一桶油注入容积是1.25升的瓶子里,需要装多少瓶?
28.春季植树活动中,长征小学的五年级学生比六年级学生少植树126棵,六年级学生植树的棵数是五年级学生的1.5倍,长征小学五、六年级学生各植树多少棵?(列方程解答)
29.一本书科技书,夏小轩同学第一天看了它的,第二天看了它的20%,这时两天一共看了135页。
(1)这本书一共有多少页?
(2)剩下的页数他计划3天看完,平均每天要看多少页?
30.甲、乙、丙三人一起参加长跑比赛,当甲跑完全程的75%时,乙才到达全程的处。这时,丙恰好跑到甲、乙两人之间的中点处,并且离终点还有875米。求这次长跑的全程是多少米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.27;130;;
0.6;;;
【详解】略
2.4100;;
1;;
【分析】4260-3840÷24,先计算除法,再计算减法;
×(1-),先计算括号里的减法,再计算乘法;
,先计算括号里的减法和加法,再计算除法;
+-(+),根据减法性质,原式化为:+--,再根据加法交换律和结合律,原式化为:(-)+(-),再进行计算;
,把除法换成乘法,原式化为:×+×,再根据乘法分配律,原式化为:×(+),再进行计算;
,先计算小括号里的减法,再计算中括号里的乘,最后计算括号外的除法。
【详解】4260-3840÷24
=4260-160
=4100
×(1-)
=×
=
=(-)÷(+)
=÷
=×
=
=
=+--
=(-)+(-)
=+
=1
=×+×
=×(+)
=×(+)
=×
=
=÷[(-)×]
=÷[×]
=÷
=×
=
3.;;
【分析】根据等式的性质,方程两边同时减5.4,再同时除以2.5;
原方程化简后得,根据等式的性质,方程两边同时除以;
根据比例的性质将原式化成方程得,根据等式的性质,方程两边同时除以0.6。
【详解】
解:
解:
解:
4.270平方厘米
【分析】如下图:
连接BE,三角形BCE的面积为:18×15÷2=135(平方厘米),而三角形BCE的面积也可以是:BC×BC边上的高÷2,BC边上的高则与CD或AB相等,从这一点可分析出长方形ABCD的面积是三角形BCE的面积的2倍,据此解答。
【详解】18×15÷2×2
=270÷2×2
=270(平方厘米)
5.C
【分析】根据从前面、右面观察到的形状可知:该长方体的长是4厘米、宽是3厘米、高是2厘米,带入长方体的体积公式计算即可。
【详解】4×3×2
=12×2
=24(立方厘米)
故答案为:C
【点睛】明确长方体的长、宽、高是解题的关键。
6.D
【分析】先求出5∶4的比值,再求出各选项图形中长与宽的比值,与5∶4的比值比较,如果相等就能组成比例;据此解答即可。
【详解】5∶4=5÷4=
A.16∶10=16÷10=,≠,所以与5∶4不能组成比例;
B.18∶15=18÷15=,≠,所以与5∶4不能组成比例;
C.12∶9=12÷9=,≠,所以与5∶4不能组成比例;
D.15∶12=15÷12=,=,所以与5∶4能组成比例。
故答案为:D
【点睛】此题考查比例意义的运用,明确比例是表示两个比相等的式子。
7.A
【分析】判断水的体积和水的高度之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;比值、乘积均不一定则不成比例;据此解答。
【详解】50∶2=50÷2=25
100∶4=100÷4=25
150∶6=150÷6=25
200∶8=200÷8=25
杯中水的体积和水的高度的比值一定,所以杯中水的体积和水的高度成正比例。
故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
8.A
【分析】根据“上北下南,左西右东”确定方向,注意观测点是盐城高铁站。再根据图上距离和比例尺的关系确定实际距离。
【详解】12×2=24(千米)
90°-30°=60°
荷兰花海在盐城高铁站的东偏南30°方向24千米处或南偏东60°方向24千米处。
故答案为:A
【点睛】本题主要考查图上距离与实际距离、比例尺的关系。
9.D
【分析】由图可知:图中表示3中包含几个,符合除法的意义。
【详解】图中表示3中包含几个,用算式表示是3÷。
故答案为:D
【点睛】本题主要考查分数除法的意义。
10.B
【分析】根据图形可知,涂色部分是长方体的一个面,有一个角是直角,所以从上面看,涂色部分是直角三角形,据此解答。
【详解】根据分析可知,洋洋制作了一个长方体纸盒,在纸盒的上面进行涂色(如图)。从上面看,涂色部分是直角三角形。
故答案为:B
【点睛】解答本题的关键是明确长方体的特征。根据三角形的分类和认识知识进行解答。
11.C
【分析】圆柱的侧面展开图是一个正方形,说明圆柱的底面周长=高,据此写出两者的比即可。
【详解】如果一个圆柱的侧面展开图是一个正方形,那么该圆柱的高和底面周长的比是1∶1。
故答案为:C
【点睛】本题考查了圆柱的展开图及比的意义,圆柱侧面沿高展开一般是长方形,当底面周长=高时,侧面沿高展开就是正方形。
12.C
【详解】设原来的长与宽的比是a∶b,
放大后的比为(a×10)∶(b×10)=a∶b;
故答案为:C。
13.C
【分析】没有红漆的面应是每次的切面,圆柱被竖着切了2刀,横着切了1刀,每切一刀都要增加8个面,所以共有8×3=24个面没有红漆,据此解答。
【详解】根据分析可得,
8×3=24(个)
所以没有红漆的面共有24个。
故答案为:C
【点睛】此题主要考查立体图形的切拼,重点理解每切一刀都要增加8个没有红漆的面。
14.A
【详解】略
15. 三百万九千七百零四 301
【分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零,即可读出此数;省略“万”后面的尾数就是四舍五入到万位,就是把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字。
【详解】3009704读作:三百万九千七百零四;3009704≈301万。
【点睛】本题主要考查整数的读法和求近似数,注意:分级读即可快速、正确地读出此数;求近似数时要带计数单位。
16.;
【分析】把一根5米长的铁丝剪成同样长的7段,求第3段的长度,用这根铁丝的长度除以剪成的段数(与段的序数无关);求每段长是1米的几分之几,用每段的长度除以1米,据此解答。
【详解】5÷7=(米)
÷1=
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称。
17. 正 3∶5
【分析】先把等积式化为比例式,再根据判断两种相关联的量成什么比例,就看两种相关量中相对应的两个数是商一定还是积一定,如果商一定,就成正比例;如果积一定,就成反比例来判断即可;把等积式化为比例式,再根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外)比值不变,进而把比化成最简比。
【详解】因为3A=1.8B(A、B均不为0),即:A÷B=0.6(一定),所以成正比例。
A∶B=1.8∶3
=(1.8÷0.6)∶(3÷0.6)
=3∶5
【点睛】本题主要考查了化简比及辨识成正比例的量与成反比例的量,解题的关键是把等积式化为比例式。
18. 471 18
【分析】根据圆柱的体积=底面积×高,圆锥的体积=底面积×高÷3,则高=圆锥的体积×3÷底面积,解答此题即可。
【详解】3.14×5×5×6
=15.7×30
=471(立方厘米)
471×3÷(3.14×5×5)
=1413÷78.5
=18(厘米)
【点睛】熟练掌握圆锥和圆柱的体积公式,是解答此题的关键。
19. 90% 92%
【分析】合格率是指合格的零件的个数占全部零件的个数的百分之几,先用“72+8”求出这批零件的总个数,然后根据公式:合格率=合格零件数÷加工的全部零件个数×100%,进行解答即可;求他加工的全部零件的合格率,先求出加工的全部的零件个数与合格零件的总个数,然后根据:合格率=合格零件数÷加工的全部零件个数×100%,进行解答即可。
【详解】72÷(72+8)×100%
=72÷80×100%
=90%
(72+20)÷(72+20+8)×100%
=92÷100×100%
=92%
【点睛】此题属于百分率问题,掌握合格率的表达式是解题的关键。
20. 35 27
【分析】此题考查学生用假设法解决问题。如果假设10个均为小盒,则要将每个大盒中多装的8个球去掉。如果假设10个均为大盒,则要将每个小盒中少掉的8个球加上。
【详解】假设10个均为小盒
302-4×8=270(个)
270÷10=27(个)
大盒装球个数:27+8=35(个)。
21. 84.56 40
【分析】根据图示可知,把圆柱沿高截成3段,表面积增加2×2=4个底面积,沿底面直径切成4块,表面积增加(2×4)个半径乘高;没有涂色的面即这些切面,是切完之后露出来的面,即(4×2×2)个圆和(2×4×3)个长方形的面。
【详解】3.14×(2÷2)2×(2×2)+(2×4)×(2÷2)×9
=3.14×4+72
=84.56(平方厘米)
4×2×2+2×4×3
=16+24
=40(个)
【点睛】本题的考查圆柱的切割问题,要求同学展开空间想象能力。
22. 76 52
【分析】由题意可知,原足球个数×+原篮球个数×=147-115,根据乘法分配律可得(原足球个数+原篮球个数)×=147-115。根据分数除法的意义,用(147-115)除以即可求出原来足球、篮球的总个数。原来两球的总个数与147个之差就是增加足球的个数,原来两球的总个数与115个之差就是增加篮球的个数。分别用两种球增加的个数除以即可求出它们各自添置的个数。
【详解】(147-115)÷
=32÷
=128(个)
147-128=19(个)
足球:19÷=76(个)
128-115=13(个)
篮球:13÷=52(个)
【点睛】解答此题的关键和难点是:明白147个与115个之差是原来两种球总个数的,然后根据分数除法的意义求出原来两种球的总个数。
23.85元
【详解】,
=25.5÷30%,
=85(元);
答:这双运动鞋的原价是85元.
【点睛】打七折是指现价是原价的70%,把原价看成单位“1”,现价比原价便宜了(1-70%),它对应的数量是25.5元,求原价用除法.
24.桃树:180÷(7-5)×3=270(棵)
梨树:270÷=450(棵)
苹果树:270÷=630(棵)
【详解】略
25.10.2吨
【分析】圆锥的体积公式为:V=Sh,在此题中,先根据底面直径是4米,进而求出底面半径,然后根据圆的面积公式求出底面积,再根据圆锥的体积公式求出圆锥的体积,最后根据“黄沙的体积×每立方米沙的重量=这堆沙的总重量”解答即可。
【详解】×3×(4÷2)2×1.5×1.7
=1×22×1.5×1.7
=4×1.5×1.7
=10.2(吨)
答:这堆黄沙大约重10.2吨。
【点睛】此题考查了圆锥体积的求解方法,要注意不要忘记乘。
26.4500立方厘米
【分析】根据长方体的棱长总和是220厘米,先求出长、宽、高的和是220÷4=55厘米,再根据长宽高的比,即可分别求出长方体的长宽高的值,利用长方体的体积公式:V=abh,代入求解即可。
【详解】长和宽的比是2∶1,可得长和宽的比是6∶3,
所以长、宽、高的比是6∶3∶2;
220÷4÷(6+3+2)
=55÷11
=5(厘米)
5×6=30(厘米)
5×3=15(厘米)
5×2=10(厘米)
30×15×10=4500(立方厘米)
答:这个长方体的体积是4500立方厘米。
【点睛】此题考查了长方体的棱长总和和长方体的体积公式的运用以及比的应用。
27.24瓶
【分析】先根据长方体的体积公式求出这样一桶油的体积是:2.5×2.5×4.8=30立方分米=30升,根据除法的意义,计算出里面有多少个1.25升,就可以装几瓶。
【详解】2.5×2.5×4.8÷1.25
=30÷1.25
=24(瓶)
答:需要装24瓶。
【点睛】此题考查长方体体积公式的计算和除法意义的灵活应用。
28.五年级252棵,六年级378棵。
【分析】根据题意可得等量关系式:五年级学生植树的棵数×1.5 =六年级学生植树的棵数,五年级学生植树的棵数+126=六年级学生植树的棵数,设五年级学生植树x棵,然后列方程解答即可。
【详解】解:设五年级学生植树x棵。
1.5x=x+126
1.5x-x=x+126-x
0.5x=126
0.5x÷0.5=126÷0.5
x=252
252×1.5=378(棵)
答:长征小学五年级学生植树252棵,六年级学生植树378棵。
【点睛】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
29.(1)300页;
(2)55页
【分析】(1)第一天看了全书总页数的,第二天看了全书总页数的20%,根据分数加法的意义,两天共看了总页数的(+20%),又知道两天一共看了135页,根据分数除法的意义,用所看页数除以其占总页数的分率,即得共有多少页;
(2)依据剩下的页数=总共的-已经看了的,求出剩下的页数,用剩下的页数除以3即可求解。
【详解】(1)135÷(+20%)
=135÷0.45
=300(页)
答:这本书一共有300页。
(300-135)÷3
=165÷3
=55(页)
答:平均每天要看55页。
【点睛】解答分数应用题的关键是找出题目中的单位“1”,再根据单位“1”的已知和未知情况,确定解答方法。
30.3000米
【分析】设全程为单位“1”,因为丙恰好跑到甲、乙两人之间的中点处,可知丙此时到达全程的(75%-)×,再加上全程剩下的(1-75%),即为875米所对应的分率,根据分数除法的意义,用除法可解答此题。
【详解】(75%-)×+(1-75%)
=(-)×+(1-)
=×+
=
875÷=3000(米)
答:这次长跑的全程是3000米。
【点睛】解答此题的关键是要找准875米所对应的分率,再用分数除法的意义去求全程。提示:如果觉得题目难以理解,也可以画线段图帮助理解题意。
答案第1页,共2页
答案第1页,共2页
