人教版九年级上册24.1.1 圆 课件 (共20张PPT)
文档属性
| 名称 | 人教版九年级上册24.1.1 圆 课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 957.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-28 07:41:29 | ||
图片预览





文档简介
(共20张PPT)
24.1.1 圆
第一课时
知识框架
圆的基本概念
圆的定义
与圆有关的概念
圆的动态定义:
圆的静态定义:
弦:
直径:
圆弧(弧):
半圆:
优弧、劣弧:
等圆:
等弧:
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆。
圆心为O、半径为r的圆可以看成是平面内所有到定点O的距离等定长r的点的集合。
连接圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
圆上任意两点间的部分叫做圆弧,简称弧。
圆的任意一条直径的两个端点把圆分成两条弧,每条弧
都叫做半圆。
能够重合的两个圆叫做等圆。
大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧。
在同圆或等圆中,能够互相重合的弧叫做等弧。
r
推进新课
知识点1
圆的动态定义
特殊的圆
O
同心圆
等圆
圆心相同,半径不等
半径相等,圆心不同
判断下列说法的正误,并说明理由或举反例。
(1)圆心相同,半径相等的两个圆是同心圆;( )
(2)半径相等的两个圆是等圆。( )
×
√
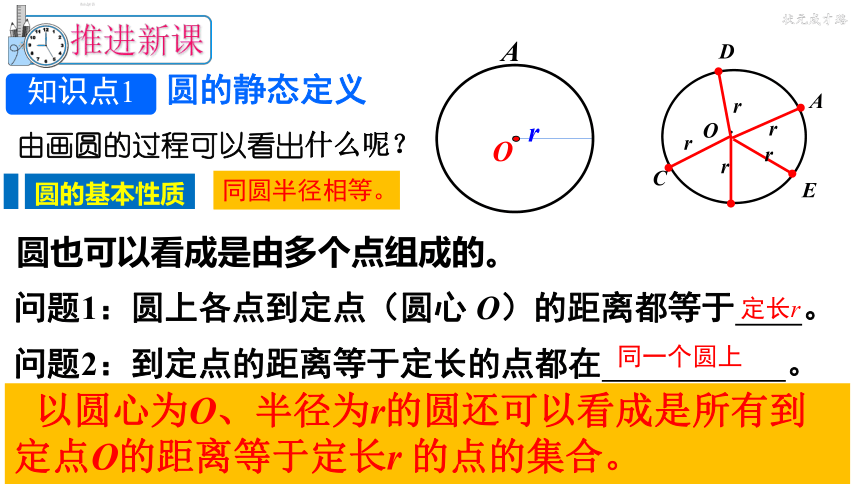
问题1:圆上各点到定点(圆心 O)的距离都等于 。
问题2:到定点的距离等于定长的点都在 。
·
r
O
A
推进新课
由画圆的过程可以看出什么呢?
以圆心为O、半径为r的圆还可以看成是所有到定点O的距离等于定长r 的点的集合。
定长r
同一个圆上
O
·
A
C
E
r
r
r
r
r
D
知识点1
圆的静态定义
圆的基本性质
同圆半径相等。
圆也可以看成是由多个点组成的。
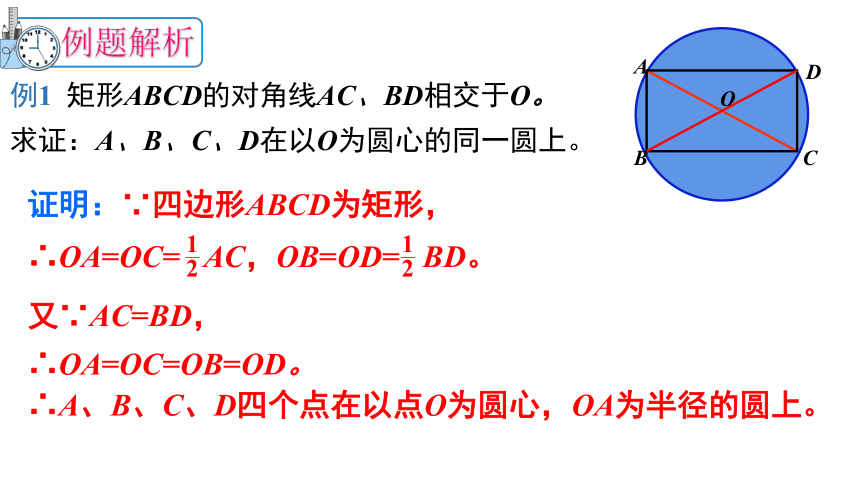
例1 矩形ABCD的对角线AC、BD相交于O。
求证:A、B、C、D在以O为圆心的同一圆上。
A
B
C
D
O
例题解析
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD。
又∵AC=BD,
∴OA=OC=OB=OD。
∴A、B、C、D四个点在以点O为圆心,OA为半径的圆上。
弦
·
C
O
A
B
推进新课
知识点2
与圆有关的概念
直径是特殊的弦。
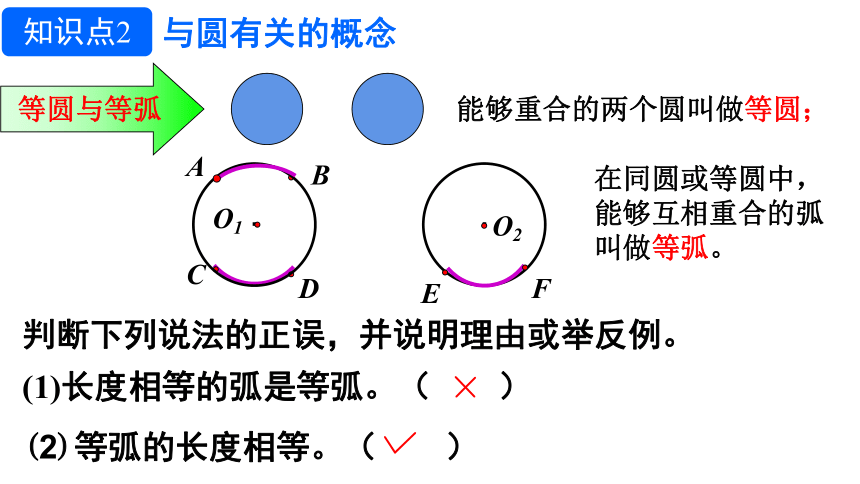
判断下列说法的正误,并说明理由或举反例。
(1)弦是直径。( )
(2)直径是弦。( )
(3)半径是弦。( )
(4)直径是圆中最长的弦。( )
√
√
弧
推进新课
知识点2
与圆有关的概念
判断下列说法的正误,并说明理由或举反例。
(1)半圆是弧。( )
(2)圆的任意一条弦把圆分成优弧和劣弧两部分。( )
等圆与等弧
能够重合的两个圆叫做等圆;
在同圆或等圆中,能够互相重合的弧叫做等弧。
·
B
O1
A
·
D
O2
F
E
C
知识点2
与圆有关的概念
判断下列说法的正误,并说明理由或举反例。
(1)长度相等的弧是等弧。( )
(2)等弧的长度相等。( )
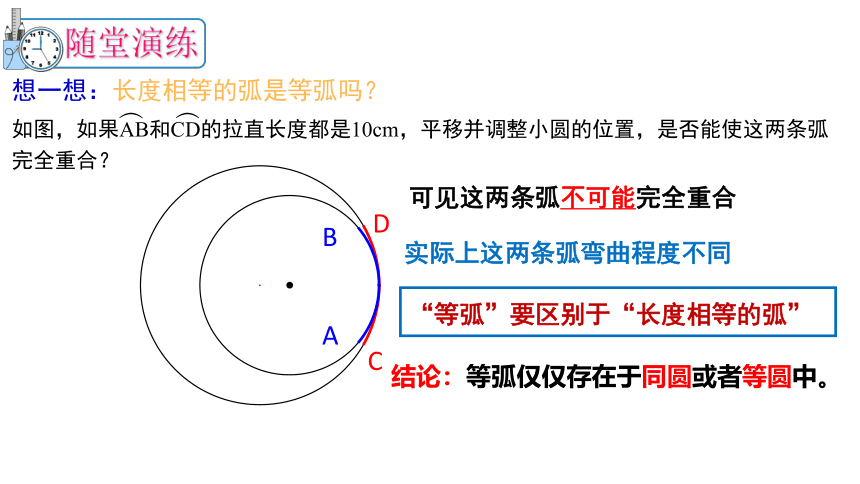
结论:等弧仅仅存在于同圆或者等圆中。
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
想一想:长度相等的弧是等弧吗?
随堂演练
随堂演练
2、一个圆的最长的弦长是10cm,则此圆的半径是 cm。
5
B
1、如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么这条圆弧所在圆的圆心是( )
A、点P B、点Q C、点R D、点M
3、如图,MN是的弦,∠MON=120°,那么∠M= 。
30°
圆
定义
旋转定义
要画一个确定的圆,关键是
确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
课堂小结
24.1.1 圆
第二课时
自主探究
1.画一个圆,观察画圆的过程,你能由此说出圆的形成过程吗?
2.观察下列图形后思考:图形中的各端点与O点的距离有什么关系?
想一想:在平面内还有到O点的距离相等的点吗?它们构成什么图形?
自主探究
弧、等弧
等弧的条件:
1.在同圆或者等圆中
2.所对的圆心角相等或长度相等
尝试运用
1、以已知点O为圆心,可以画 个圆;以已知线段AB的长为半径,可以画 个圆.
2、已知⊙O中最长的弦为10cm,则⊙O的半径为 cm.
3、如下图所示,在⊙O中,AB为直径,P点为OB上一点(不同于O、B),CD、EF是⊙O中过点P的两条弦,则图中有 条直径, 条非直径的弦,以A为一个端点的劣弧有 条.
4、下列判断中,不正确的个数是( ).
①直径是弦;②弧包括优弧和劣弧;③等弧是长度相等的弧;④经过圆内一定点可以作无数条直径.
A.1个 B.2个 C.3个 D.4个
5、设AB=3cm,画图说明具有下列性质的点的集合是怎样的图形.
(1)和点A的距离等于2cm的点的集合;
(2)和点B的距离等于2cm的点的集合;
(3)和点A,B的距离都等于2cm的点的集合;
(4)和点A,B的距离都小于2cm的点的集合.
D
尝试运用
6.思考:车轮为什么做成圆形的?如果车轮不是圆的(比如椭圆或正方形),坐车的人会是什么感觉?
尝试运用
补偿提高
1、以已知点O为圆心,已知线段a为半径作圆,可以作( )。
A.1个 B.2个 C.3个 D.无数个
2、点P到圆上各点的最大距离是8cm,最小距离是6cm,则圆的半径是( ).
A.7 cm B.1 cm C.7 cm或1 cm D.无法确定
3、如图,⊙O的半径为3 cm,A为⊙O上一定点,P在⊙O上沿圆周运动(不与A重合),则弦AP的长度为整数值的有 个,这样的弦共有 条.
A
O
B
.
A
A
6
11
谢谢聆听
24.1.1 圆
第一课时
知识框架
圆的基本概念
圆的定义
与圆有关的概念
圆的动态定义:
圆的静态定义:
弦:
直径:
圆弧(弧):
半圆:
优弧、劣弧:
等圆:
等弧:
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆。
圆心为O、半径为r的圆可以看成是平面内所有到定点O的距离等定长r的点的集合。
连接圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
圆上任意两点间的部分叫做圆弧,简称弧。
圆的任意一条直径的两个端点把圆分成两条弧,每条弧
都叫做半圆。
能够重合的两个圆叫做等圆。
大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧。
在同圆或等圆中,能够互相重合的弧叫做等弧。
r
推进新课
知识点1
圆的动态定义
特殊的圆
O
同心圆
等圆
圆心相同,半径不等
半径相等,圆心不同
判断下列说法的正误,并说明理由或举反例。
(1)圆心相同,半径相等的两个圆是同心圆;( )
(2)半径相等的两个圆是等圆。( )
×
√
问题1:圆上各点到定点(圆心 O)的距离都等于 。
问题2:到定点的距离等于定长的点都在 。
·
r
O
A
推进新课
由画圆的过程可以看出什么呢?
以圆心为O、半径为r的圆还可以看成是所有到定点O的距离等于定长r 的点的集合。
定长r
同一个圆上
O
·
A
C
E
r
r
r
r
r
D
知识点1
圆的静态定义
圆的基本性质
同圆半径相等。
圆也可以看成是由多个点组成的。
例1 矩形ABCD的对角线AC、BD相交于O。
求证:A、B、C、D在以O为圆心的同一圆上。
A
B
C
D
O
例题解析
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD。
又∵AC=BD,
∴OA=OC=OB=OD。
∴A、B、C、D四个点在以点O为圆心,OA为半径的圆上。
弦
·
C
O
A
B
推进新课
知识点2
与圆有关的概念
直径是特殊的弦。
判断下列说法的正误,并说明理由或举反例。
(1)弦是直径。( )
(2)直径是弦。( )
(3)半径是弦。( )
(4)直径是圆中最长的弦。( )
√
√
弧
推进新课
知识点2
与圆有关的概念
判断下列说法的正误,并说明理由或举反例。
(1)半圆是弧。( )
(2)圆的任意一条弦把圆分成优弧和劣弧两部分。( )
等圆与等弧
能够重合的两个圆叫做等圆;
在同圆或等圆中,能够互相重合的弧叫做等弧。
·
B
O1
A
·
D
O2
F
E
C
知识点2
与圆有关的概念
判断下列说法的正误,并说明理由或举反例。
(1)长度相等的弧是等弧。( )
(2)等弧的长度相等。( )
结论:等弧仅仅存在于同圆或者等圆中。
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
想一想:长度相等的弧是等弧吗?
随堂演练
随堂演练
2、一个圆的最长的弦长是10cm,则此圆的半径是 cm。
5
B
1、如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么这条圆弧所在圆的圆心是( )
A、点P B、点Q C、点R D、点M
3、如图,MN是的弦,∠MON=120°,那么∠M= 。
30°
圆
定义
旋转定义
要画一个确定的圆,关键是
确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
课堂小结
24.1.1 圆
第二课时
自主探究
1.画一个圆,观察画圆的过程,你能由此说出圆的形成过程吗?
2.观察下列图形后思考:图形中的各端点与O点的距离有什么关系?
想一想:在平面内还有到O点的距离相等的点吗?它们构成什么图形?
自主探究
弧、等弧
等弧的条件:
1.在同圆或者等圆中
2.所对的圆心角相等或长度相等
尝试运用
1、以已知点O为圆心,可以画 个圆;以已知线段AB的长为半径,可以画 个圆.
2、已知⊙O中最长的弦为10cm,则⊙O的半径为 cm.
3、如下图所示,在⊙O中,AB为直径,P点为OB上一点(不同于O、B),CD、EF是⊙O中过点P的两条弦,则图中有 条直径, 条非直径的弦,以A为一个端点的劣弧有 条.
4、下列判断中,不正确的个数是( ).
①直径是弦;②弧包括优弧和劣弧;③等弧是长度相等的弧;④经过圆内一定点可以作无数条直径.
A.1个 B.2个 C.3个 D.4个
5、设AB=3cm,画图说明具有下列性质的点的集合是怎样的图形.
(1)和点A的距离等于2cm的点的集合;
(2)和点B的距离等于2cm的点的集合;
(3)和点A,B的距离都等于2cm的点的集合;
(4)和点A,B的距离都小于2cm的点的集合.
D
尝试运用
6.思考:车轮为什么做成圆形的?如果车轮不是圆的(比如椭圆或正方形),坐车的人会是什么感觉?
尝试运用
补偿提高
1、以已知点O为圆心,已知线段a为半径作圆,可以作( )。
A.1个 B.2个 C.3个 D.无数个
2、点P到圆上各点的最大距离是8cm,最小距离是6cm,则圆的半径是( ).
A.7 cm B.1 cm C.7 cm或1 cm D.无法确定
3、如图,⊙O的半径为3 cm,A为⊙O上一定点,P在⊙O上沿圆周运动(不与A重合),则弦AP的长度为整数值的有 个,这样的弦共有 条.
A
O
B
.
A
A
6
11
谢谢聆听
同课章节目录
