【最新强化训练】沪教版(上海)九下 第二十七章圆与正多边形定向训练试题(无超纲,含解析)
文档属性
| 名称 | 【最新强化训练】沪教版(上海)九下 第二十七章圆与正多边形定向训练试题(无超纲,含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 11:35:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十七章圆与正多边形定向训练
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域 ( http: / / www.21cnjy.com )内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【出处:21教育名师】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,面积为18的正方形ABCD内接于⊙O,则⊙O的半径为( )
( http: / / www.21cnjy.com / )
A. B.
C.3 D.
2、如图,在中,,,.将绕点按逆时针方向旋转后得到,则图中阴影部分面积为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. B. C. D.
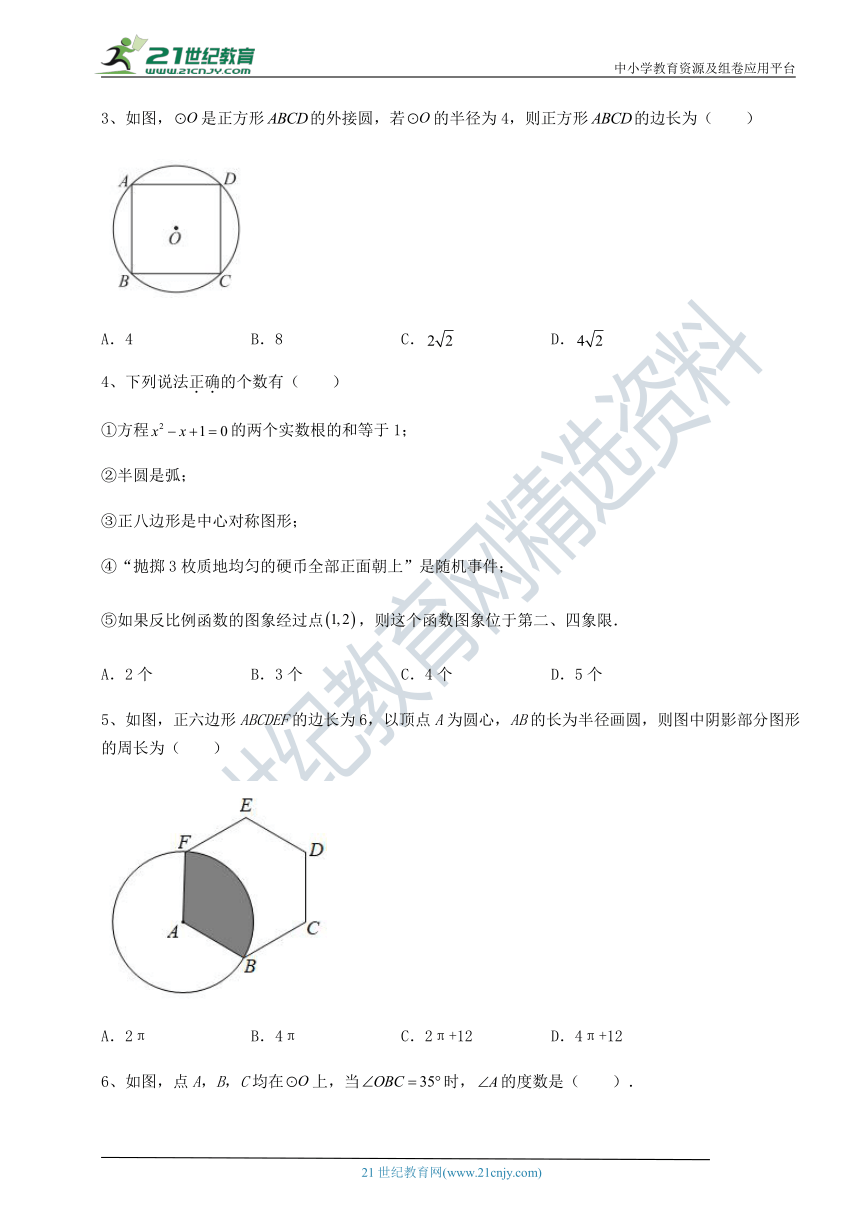
3、如图,是正方形的外接圆,若的半径为4,则正方形的边长为( )
( http: / / www.21cnjy.com / )
A.4 B.8 C. D.
4、下列说法正确的个数有( )
①方程的两个实数根的和等于1;
②半圆是弧;
③正八边形是中心对称图形;
④“抛掷3枚质地均匀的硬币全部正面朝上”是随机事件;
⑤如果反比例函数的图象经过点,则这个函数图象位于第二、四象限.
A.2个 B.3个 C.4个 D.5个
5、如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分图形的周长为( )
( http: / / www.21cnjy.com / )
A.2π B.4π C.2π+12 D.4π+12
6、如图,点A,B,C均在上,当时,的度数是( ).
( http: / / www.21cnjy.com / )
A.65° B.60° C.55° D.50°
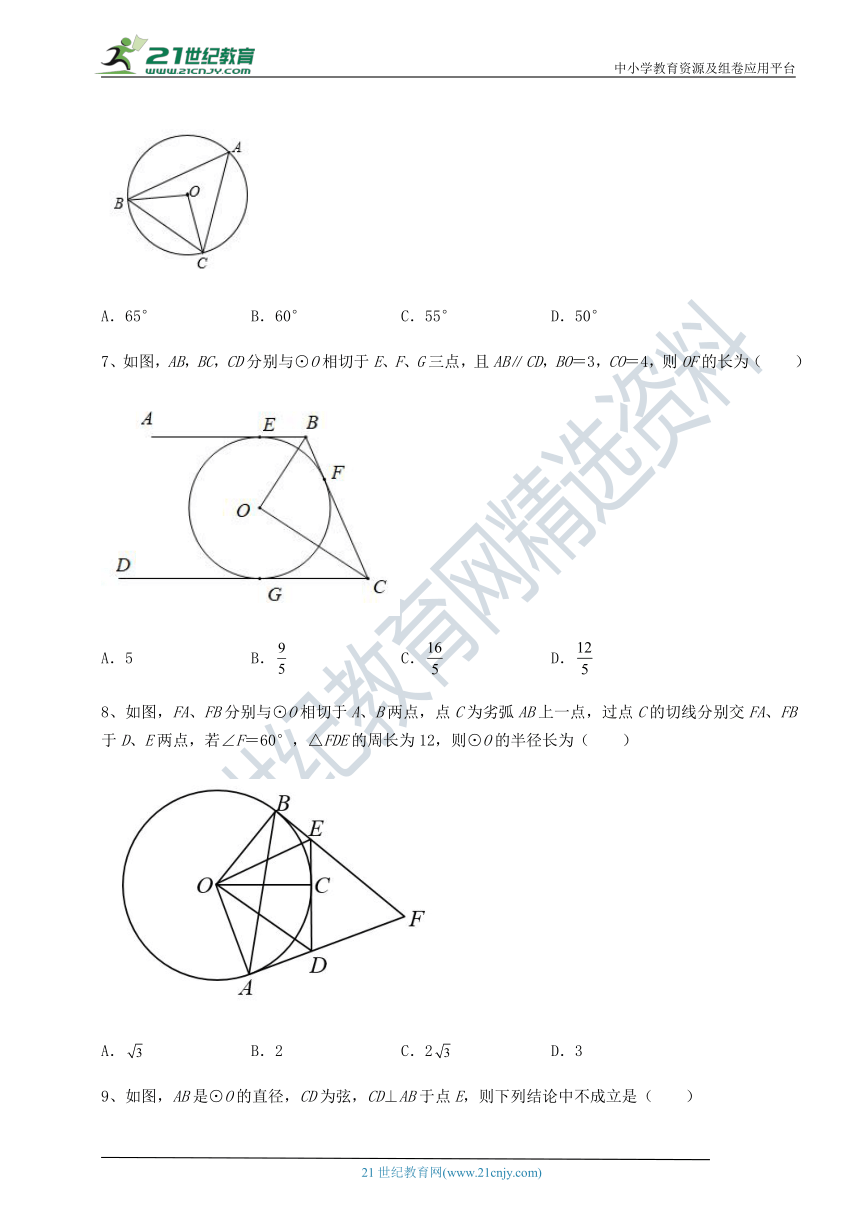
7、如图,AB,BC,CD分别与⊙O相切于E、F、G三点,且ABCD,BO=3,CO=4,则OF的长为( )
( http: / / www.21cnjy.com / )
A.5 B. C. D.
8、如图,FA、FB分别 ( http: / / www.21cnjy.com )与⊙O相切于A、B两点,点C为劣弧AB上一点,过点C的切线分别交FA、FB于D、E两点,若∠F=60°,△FDE的周长为12,则⊙O的半径长为( )
( http: / / www.21cnjy.com / )
A. B.2 C.2 D.3
9、如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立是( )
( http: / / www.21cnjy.com / )
A.弧AC=弧AD B.弧BC=弧BD C.CE=DE D.OE=BE
10、如图,正方形ABCD内接于⊙O,点P在上,则下列角中可确定大小的是( )
( http: / / www.21cnjy.com / )
A.∠PCB B.∠PBC C.∠BPC D.∠PBA
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
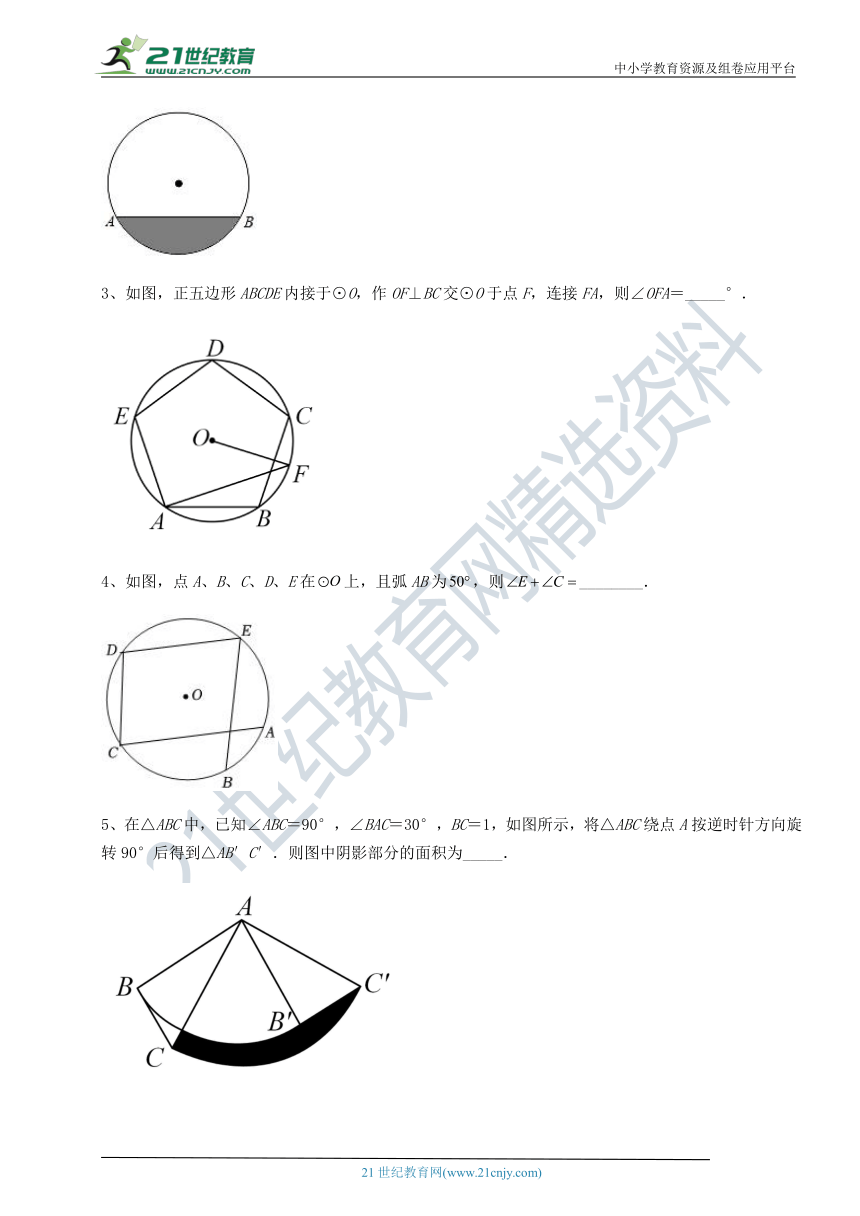
1、如图,半圆O中,直径AB=30,弦CD∥AB,长为6π,则由与AC,AD围成的阴影部分面积为_______.
( http: / / www.21cnjy.com / )
2、往直径为26cm的圆柱形容器内装入一些水以后,截面如图所示,若水的最大深度为8cm,则水面AB的宽度为___cm.
( http: / / www.21cnjy.com / )
3、如图,正五边形ABCDE内接于⊙O,作OF⊥BC交⊙O于点F,连接FA,则∠OFA=_____°.
( http: / / www.21cnjy.com / )
4、如图,点A、B、C、D、E在上,且弧AB为,则________.
( http: / / www.21cnjy.com / )
5、在△ABC中,已知∠ABC= ( http: / / www.21cnjy.com )90°,∠BAC=30°,BC=1,如图所示,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分的面积为_____.21cnjy.com
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、如图,四边形ABCD内接⊙O,∠C=∠B.
( http: / / www.21cnjy.com / )
(1)如图1,求证:AB=CD;
(2)如图2,连接BO并延长分别交⊙O和CD于点F、E,若CD=EB,CD⊥EB,求tan∠CBF;
(3)如图3,在(2)的条件下,在BF上取点G,连接CG并延长交⊙O于点I,交AB于H,EF∶BG=1∶3,EG=2,求GH的长.
2、如图,AB为的直径,点C,D在上,,.求证:DE是的切线.
( http: / / www.21cnjy.com / )
3、如图,以点为圆心,长为直径作圆,在上取一点,延长至点,连接,,过点作交的延长线于点.
( http: / / www.21cnjy.com / )
(1)求证:是的切线;
(2)若,,求的长.
4、如图,在平面直角坐标系中,经过原点,且与轴交于点,与轴交于点,点在第二象限上,且,则__.
( http: / / www.21cnjy.com / )
5、如图,已知是的直径,是的切线,C为切点,交于点E,,,平分.
( http: / / www.21cnjy.com / )
(1)求证:;
(2)求、的长.
-参考答案-
一、单选题
1、C
【分析】
连接OA、OB,则为等腰直角三角形,由正方形面积为18,可求边长为,进而通过勾股定理,可得半径为3.
【详解】
解:如图,连接OA,OB,则OA=OB,
( http: / / www.21cnjy.com / )
∵四边形ABCD是正方形,
∴,
∴是等腰直角三角形,
∵正方形ABCD的面积是18,
∴,
∴,即:
∴
故选C.
【点睛】
本题考查了正多边形和圆、正方形的性质等知识,构造等腰直角三角形是解题的关键.
2、B
【分析】
阴影部分的面积=扇形扇形,根据旋转性质以及直角三角形的性质,分别求出对应扇形的面积以及的面积,最后即可求出阴影部分的面积.
【详解】
解:由图可知:阴影部分的面积=扇形扇形,
由旋转性质可知:,,
,,
在中,,,,
,,
有勾股定理可知:,
阴影部分的面积=扇形扇形
.
故选:B.
【点睛】
本题主要是考查了旋转性质以及扇形面积公式,熟练利用旋转性质,得到对应扇形的半径和圆心角度数,利用扇形公式求解面积,这是解决本题的关键.
3、D
【分析】
连接OB,OC,过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
【详解】
解:连接OB,OC,过点O作OE⊥BC于点E,
( http: / / www.21cnjy.com / )
∴OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴,
∴BC=2BE=,即正方形ABCD的边长是.
故选:D
【点睛】
本题考查的是圆周角定理、垂径定理及勾股定理,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.
4、B
【分析】
根据所学知识对五个命题进行判断即可.
【详解】
1、,故方程无实数根,故本命题错误;
2、圆上任意两点间的部分叫做圆弧,半圆也是,故本命题正确;
3、八边形绕中心旋转180°以后仍然与原图重合,故本命题正确;
4、抛硬币无论抛多少,出现正反面朝上都是随机事件,故抛三枚硬币全部正面朝上也是随机事件,故本命题正确;
5、反比例函数的图象经过点 (1,2) ,则,它的函数图像位于一三象限,故本命题错误
综上所述,正确个数为3
故选B
【点睛】
本题考查一元二次函数判别式、弧的定义、中心对称图形判断、随机事件理解、反比例函数图像,掌握这些是本题关键.
5、D
【分析】
根据正多边形的外角求得内角的度数,进而根据弧长公式求得,即可求得阴影部分的周长.
【详解】
解:正六边形ABCDEF的边长为6,
阴影部分图形的周长为
故选D
【点睛】
本题考查了求弧长公式,求正多边形的内角,牢记弧长公式和正多边形的外角与内角的关系是解题的关键.
6、C
【分析】
先由OB=OC,得到∠OCB=∠OBC=35°,从而可得∠BOC=180°-∠OCB-∠OBC=110°,再由圆周角定理即可得到答案.
【详解】
解:∵OB=OC,
∴∠OCB=∠OBC=35°,
∴∠BOC=180°-∠OCB-∠OBC=110°,
∴,
故选C.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了圆周角定理,三角形内角和定理,等腰三角形的性质,熟知圆周角定理是解题的关键.
7、D
【分析】
连接OF,OE,OG,根据切线的性质及角平分线的判定可得OB平分,OC平分,利用平行线的性质及角之间的关系得出,利用勾股定理得出,再由三角形的等面积法即可得.
【详解】
解:连接OF,OE,OG,
( http: / / www.21cnjy.com / )
∵AB、BC、CD分别与相切,
∴,,,且,
∴OB平分,OC平分,
∴,,
∵,
∴,
∴,
∴,
,
∴,
∴,
故选:D.
【点睛】
题目主要考查圆的切线性质,角平分线的判定和性质,平行线的性质,勾股定理等,理解题意,作出辅助线,综合运用这些知识点是解题关键.21教育名师原创作品
8、C
【分析】
根据切线长定理可得,、、,再根据∠F=60°,可知为等边三角形,,再△FDE的周长为12,可得,求得,再作,即可求解.
【详解】
解:FA、FB分别与⊙O相切于A、B两点,过点C的切线分别交FA、FB于D、E两点,
则:、、,,
∵∠F=60°,
∴为等边三角形,,
∵△FDE的周长为12,即,
∴,即,
作,如下图:
( http: / / www.21cnjy.com / )
则,,
∴,
设,则,由勾股定理可得:,
解得,,
故选C
【点睛】
此题考查了圆的有关性质,切线的性质、切线长定理,垂径定理以及等边三角形的判定与性质,解题的关键是灵活运用相关性质进行求解.【版权所有:21教育】
9、D
【分析】
根据垂径定理解答.
【详解】
解:∵AB是⊙O的直径,CD为弦,CD⊥AB于点E,
∴弧AC=弧AD,弧BC=弧BD,CE=DE,
故选:D.
【点睛】
此题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧,熟记定理是解题的关键.
10、C
【分析】
由题意根据正方形的性质得到BC弧所对的圆心角为90°,则∠BOC=90°,然后根据圆周角定理进行分析求解.
【详解】
解:连接OB、OC,如图,
( http: / / www.21cnjy.com / )
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,
∴∠BPC=∠BOC=45°.
故选:C.
【点睛】
本题考查圆周角定理和正方形的性质,确定BC弧所对的圆心角为90°是解题的关键.
二、填空题
1、45
【分析】
连接OC,OD,根据同底等高可知S△ACD=S△OCD,把阴影部分的面积转化为扇形OCD的面积,利用扇形的面积公式S=来求解.www-2-1-cnjy-com
【详解】
解:连接OC,OD,
( http: / / www.21cnjy.com / )
∵直径AB=30,
∴OC=OD=,
∴CD∥AB,
∴S△ACD=S△OCD,
∵长为6π,
∴阴影部分的面积为S阴影=S扇形OCD=,
故答案为:45π.
【点睛】
本题主要考查了扇形的面积公式,正确理解阴影部分的面积=扇形COD的面积是解题的关键.
2、24
【分析】
连接OA,过点O作OD⊥AB交AB于点C交⊙O于D,再根据勾股定理求出AC的长,进而可得出AB的长.
【详解】
解:连接OA,过点O作OD⊥AB交AB于点C交⊙O于D.
( http: / / www.21cnjy.com / )
∵OC⊥AB,
∴AC=CB,
∵OA=OD=13cm,CD=8cm,
∴OC=OD﹣CD=5(cm),
∴,
∴AB=2AC=24(cm),
故答案为:24.
【点睛】
本题主要考查垂径定理,掌握垂径定理和勾股定理是解题的关键.
3、36
【分析】
连接OA,OB,OB交AF ( http: / / www.21cnjy.com )于J.由正多边形中心角、垂径定理、圆周角定理得出∠AOB=72°,∠BOF=36°,再由等腰三角形的性质得出答案.2-1-c-n-j-y
【详解】
解:连接OA,OB,OB交AF于J.
∵五边形ABCDE是正五边形,OF⊥BC,
∴,
∴∠AOB=72°,∠BOF=∠AOB=36°,
∴∠AOF=∠AOB +∠BOF=108°,
∵OA=OF,
∴∠OAF=∠OFA==36°
( http: / / www.21cnjy.com / )
故答案为:36.
【点睛】
本题主要考查了园内正多边形中心角度数、垂径定理和圆周角定理,垂直于弦的直径平分这条弦,并且平分弦所对的两条弧,垂径定理常与勾股定理以及圆周角定理相结合来解题.正n边形的每个中心角都等于.21·cn·jy·com
4、
【分析】
先根据弧的度数与它所对应的圆心角的度数的关系,求得弧对应的圆心角的度数,再根据圆周角与圆心角的关系,则可求得.www.21-cn-jy.com
【详解】
弧的度数等于它所对应的圆心角的度数,由于弧为,所以 ,
顶点在圆上且两边都和圆相交的角叫做圆周角,而一条弧所对的圆周角等于它所对的圆心角的一半,所以:
, ,
,
故答案为:.
( http: / / www.21cnjy.com / )
【点睛】
本题考查弧、圆周角、圆心角的概念,及它们之间的关系,熟知同弧所对的圆周角等于圆心角的一半是解本题的关键.
5、
【分析】
利用勾股定理求出AC及AB的长,根据阴影面积等于求出答案.
【详解】
解:由旋转得,,=∠BAC=30°,
∵∠ABC=90°,∠BAC=30°,BC=1,
∴AC=2BC=2,AB=,,
∴阴影部分的面积=
=,
故答案为:.
. ( http: / / www.21cnjy.com / )
【点睛】
此题考查了求不规则图形的面积,正确掌握勾股定理、30度角直角三角形的性质、扇形面积计算公式及分析出阴影面积的构成特点是解题的关键.
三、解答题
1、(1)见解析;(2);(3)
【分析】
(1)过点D作DE∥AB交BC ( http: / / www.21cnjy.com )于E,由圆内接四边形对角互补可以推出∠B+∠A=180°,证得AD∥BC,则四边形ABED是平行四边形,即可得到AB=DE,∠DEC=∠B=∠C,这DE=CD=AB;
(2)连接OC,FC,设BE=CD=2x,OB=OC=OF=r,则OE=BE-BO=2x-r,EF=BF-BE=2r-2x,由垂径定理可得,∠CEB=∠CEF=∠FCB=90°,则∠FBC+∠F=∠FCE+∠F=90°,可得∠FBC=∠FCE;由勾股定理得,则,
解得,则;
(3)EF:BG=1:3,即则 解得,则,,,如图所示,以B为圆心,以BC所在的直线为x轴建立平面直角坐标系,分别过点A作AM⊥BC与M,过点G作GN⊥BC与N,连接FC,分别求出G点坐标为,C点坐标为;A点坐标为
然后求出直线CG的解析式为,直线AB的解析式为,即可得到H的坐标为(,),则.
【详解】
解:(1)如图所示,过点D作DE∥AB交BC于E,
∵四边形ABCD是圆O的圆内接四边形,
∴∠A+∠C=180°,
∵∠B=∠C,
∴∠B+∠A=180°,
∴AD∥BC,
∴四边形ABED是平行四边形,
∴AB=DE,∠DEC=∠B=∠C,
∴DE=CD=AB;
( http: / / www.21cnjy.com / )
(2)如图所示,连接OC,FC,
设BE=CD=2x,OB=OC=OF=r,则OE=BE-BO=2x-r,EF=BF-BE=2r-2x21教育网
∵CD⊥EB,BF是圆O的直径,
∴,∠CEB=∠CEF=∠FCB=90°,
∴∠FBC+∠F=∠FCE+∠F=90°,
∴∠FBC=∠FCE;
∵,
∴,
∴,
解得,
∴;
( http: / / www.21cnjy.com / )
(3)∵EF:BG=1:3,即
∴ ,即
∴,
解得,
∴,
∴,,
如图所示,以B为圆心,以BC所在的直线为x轴建立平面直角坐标系,分别过点A作AM⊥BC与M,过点G作GN⊥BC与N,连接FC,2·1·c·n·j·y
∴,
∴,,
∵,
∴,,
∴,,
∴,,
∴G点坐标为(,),C点坐标为(,0);
∵,
∴,
∵∠ABC=∠ECB,
∴,
∴,
∵,
∴,
∴,
∴,
∴A点坐标为(,)
设直线CG的解析式为,直线AB的解析式为,
∴,,
∴,,
∴直线CG的解析式为,直线AB的解析式为,
联立,
解得,
∴H的坐标为(,),
∴.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了圆内接四边 ( http: / / www.21cnjy.com )形的性质,平行四边形的性质与判定,等腰三角形的性质与判定,解直角三角形,一次函数与几何综合,垂径定理,勾股定理,两点距离公式,解题的关键在于能够正确作出辅助线,利用数形结合的思想求解.【来源:21·世纪·教育·网】
2、见解析
【分析】
连接OD,根据已知条件得到,根据等腰三角形的性质得到∠ADO=∠DAB=30°,得到∠EDA=60°,求得OD⊥DE,于是得到结论.21·世纪*教育网
【详解】
证明:连接OD,
∵,
∴.
∵,
∴.
∵,
∴.
∵,
∴.
∴.
∴.
∴.
∴.
∴DE是的切线.
( http: / / www.21cnjy.com / )
【点睛】
本题考查了切线的判定和性质,圆周角定理,正确的作出辅助线是解题的关键.
3、(1)证明见解析;(2).
【分析】
(1)连接,先根据圆周角定理可得,再根据等腰三角形的性质可得,从而可得,然后根据角的和差可得,最后根据圆的切线的判定定理即可得证;21*cnjy*com
(2)设的半径为,先在中,利用勾股定理可求出的值,从而可得的长,再根据相似三角形的判定证出,然后根据相似三角形的性质即可得.【来源:21cnj*y.co*m】
【详解】
证明:(1)如图,连接,
( http: / / www.21cnjy.com / )
是的直径,
,
,
,
,
,
,
,即,
又是的半径,
是的切线;
(2)设的半径为,则,
,
,
在中,,即,
解得,
,
在和中,,
,
,即,
解得.
【点睛】
本题考查了圆周角定理、圆的切线的判定定理、相似三角形的判定与性质等知识点,熟练掌握圆的切线的判定定理和相似三角形的判定是解题关键.
4、2+
【分析】
连接AC,CM,AB,过点C作CH⊥OA于H,设OC=a.利用勾股定理构建方程解决问题即可.
【详解】
解:连接AC,CM,AB,过点C作CH⊥OA于H,设OC=a.
( http: / / www.21cnjy.com / )
∵∠AOB=90°,
∴AB是直径,
∵A(-4,0),B(0,2),
∴,
∵∠AMC=2∠AOC=120°,
,
在Rt△COH中,,
,
在Rt△ACH中,AC2=AH2+CH2,
∴,
∴a=2+ 或2-(因为OC>OB,所以2-舍弃),
∴OC=2+,
故答案为:2+.
【点睛】
本题考查圆周角定理,勾股定理,解直角三角形等知识,解题的关键是学会利用参数构建方程解决问题.
5、(1)90°;(2)AC=,DE=1
【分析】
(1)如图,,可知.
(2),可求出的长;,,可求出的长.
【详解】
解(1)证明如图所示,连接,,
( http: / / www.21cnjy.com / )
是直径,是的切线,平分
∴,
∴
∴.
(2)解∵,
∴
∴,
∴.
在中
∵,
∴
∴,
∴.
【点睛】
本题考查了角平分线、勾股定理、等腰三角形的性质、三角形相似的判定等知识点.解题的关键在于判定三角形相似.21*cnjy*com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十七章圆与正多边形定向训练
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域 ( http: / / www.21cnjy.com )内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【出处:21教育名师】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,面积为18的正方形ABCD内接于⊙O,则⊙O的半径为( )
( http: / / www.21cnjy.com / )
A. B.
C.3 D.
2、如图,在中,,,.将绕点按逆时针方向旋转后得到,则图中阴影部分面积为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. B. C. D.
3、如图,是正方形的外接圆,若的半径为4,则正方形的边长为( )
( http: / / www.21cnjy.com / )
A.4 B.8 C. D.
4、下列说法正确的个数有( )
①方程的两个实数根的和等于1;
②半圆是弧;
③正八边形是中心对称图形;
④“抛掷3枚质地均匀的硬币全部正面朝上”是随机事件;
⑤如果反比例函数的图象经过点,则这个函数图象位于第二、四象限.
A.2个 B.3个 C.4个 D.5个
5、如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分图形的周长为( )
( http: / / www.21cnjy.com / )
A.2π B.4π C.2π+12 D.4π+12
6、如图,点A,B,C均在上,当时,的度数是( ).
( http: / / www.21cnjy.com / )
A.65° B.60° C.55° D.50°
7、如图,AB,BC,CD分别与⊙O相切于E、F、G三点,且ABCD,BO=3,CO=4,则OF的长为( )
( http: / / www.21cnjy.com / )
A.5 B. C. D.
8、如图,FA、FB分别 ( http: / / www.21cnjy.com )与⊙O相切于A、B两点,点C为劣弧AB上一点,过点C的切线分别交FA、FB于D、E两点,若∠F=60°,△FDE的周长为12,则⊙O的半径长为( )
( http: / / www.21cnjy.com / )
A. B.2 C.2 D.3
9、如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立是( )
( http: / / www.21cnjy.com / )
A.弧AC=弧AD B.弧BC=弧BD C.CE=DE D.OE=BE
10、如图,正方形ABCD内接于⊙O,点P在上,则下列角中可确定大小的是( )
( http: / / www.21cnjy.com / )
A.∠PCB B.∠PBC C.∠BPC D.∠PBA
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,半圆O中,直径AB=30,弦CD∥AB,长为6π,则由与AC,AD围成的阴影部分面积为_______.
( http: / / www.21cnjy.com / )
2、往直径为26cm的圆柱形容器内装入一些水以后,截面如图所示,若水的最大深度为8cm,则水面AB的宽度为___cm.
( http: / / www.21cnjy.com / )
3、如图,正五边形ABCDE内接于⊙O,作OF⊥BC交⊙O于点F,连接FA,则∠OFA=_____°.
( http: / / www.21cnjy.com / )
4、如图,点A、B、C、D、E在上,且弧AB为,则________.
( http: / / www.21cnjy.com / )
5、在△ABC中,已知∠ABC= ( http: / / www.21cnjy.com )90°,∠BAC=30°,BC=1,如图所示,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分的面积为_____.21cnjy.com
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、如图,四边形ABCD内接⊙O,∠C=∠B.
( http: / / www.21cnjy.com / )
(1)如图1,求证:AB=CD;
(2)如图2,连接BO并延长分别交⊙O和CD于点F、E,若CD=EB,CD⊥EB,求tan∠CBF;
(3)如图3,在(2)的条件下,在BF上取点G,连接CG并延长交⊙O于点I,交AB于H,EF∶BG=1∶3,EG=2,求GH的长.
2、如图,AB为的直径,点C,D在上,,.求证:DE是的切线.
( http: / / www.21cnjy.com / )
3、如图,以点为圆心,长为直径作圆,在上取一点,延长至点,连接,,过点作交的延长线于点.
( http: / / www.21cnjy.com / )
(1)求证:是的切线;
(2)若,,求的长.
4、如图,在平面直角坐标系中,经过原点,且与轴交于点,与轴交于点,点在第二象限上,且,则__.
( http: / / www.21cnjy.com / )
5、如图,已知是的直径,是的切线,C为切点,交于点E,,,平分.
( http: / / www.21cnjy.com / )
(1)求证:;
(2)求、的长.
-参考答案-
一、单选题
1、C
【分析】
连接OA、OB,则为等腰直角三角形,由正方形面积为18,可求边长为,进而通过勾股定理,可得半径为3.
【详解】
解:如图,连接OA,OB,则OA=OB,
( http: / / www.21cnjy.com / )
∵四边形ABCD是正方形,
∴,
∴是等腰直角三角形,
∵正方形ABCD的面积是18,
∴,
∴,即:
∴
故选C.
【点睛】
本题考查了正多边形和圆、正方形的性质等知识,构造等腰直角三角形是解题的关键.
2、B
【分析】
阴影部分的面积=扇形扇形,根据旋转性质以及直角三角形的性质,分别求出对应扇形的面积以及的面积,最后即可求出阴影部分的面积.
【详解】
解:由图可知:阴影部分的面积=扇形扇形,
由旋转性质可知:,,
,,
在中,,,,
,,
有勾股定理可知:,
阴影部分的面积=扇形扇形
.
故选:B.
【点睛】
本题主要是考查了旋转性质以及扇形面积公式,熟练利用旋转性质,得到对应扇形的半径和圆心角度数,利用扇形公式求解面积,这是解决本题的关键.
3、D
【分析】
连接OB,OC,过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
【详解】
解:连接OB,OC,过点O作OE⊥BC于点E,
( http: / / www.21cnjy.com / )
∴OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴,
∴BC=2BE=,即正方形ABCD的边长是.
故选:D
【点睛】
本题考查的是圆周角定理、垂径定理及勾股定理,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.
4、B
【分析】
根据所学知识对五个命题进行判断即可.
【详解】
1、,故方程无实数根,故本命题错误;
2、圆上任意两点间的部分叫做圆弧,半圆也是,故本命题正确;
3、八边形绕中心旋转180°以后仍然与原图重合,故本命题正确;
4、抛硬币无论抛多少,出现正反面朝上都是随机事件,故抛三枚硬币全部正面朝上也是随机事件,故本命题正确;
5、反比例函数的图象经过点 (1,2) ,则,它的函数图像位于一三象限,故本命题错误
综上所述,正确个数为3
故选B
【点睛】
本题考查一元二次函数判别式、弧的定义、中心对称图形判断、随机事件理解、反比例函数图像,掌握这些是本题关键.
5、D
【分析】
根据正多边形的外角求得内角的度数,进而根据弧长公式求得,即可求得阴影部分的周长.
【详解】
解:正六边形ABCDEF的边长为6,
阴影部分图形的周长为
故选D
【点睛】
本题考查了求弧长公式,求正多边形的内角,牢记弧长公式和正多边形的外角与内角的关系是解题的关键.
6、C
【分析】
先由OB=OC,得到∠OCB=∠OBC=35°,从而可得∠BOC=180°-∠OCB-∠OBC=110°,再由圆周角定理即可得到答案.
【详解】
解:∵OB=OC,
∴∠OCB=∠OBC=35°,
∴∠BOC=180°-∠OCB-∠OBC=110°,
∴,
故选C.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了圆周角定理,三角形内角和定理,等腰三角形的性质,熟知圆周角定理是解题的关键.
7、D
【分析】
连接OF,OE,OG,根据切线的性质及角平分线的判定可得OB平分,OC平分,利用平行线的性质及角之间的关系得出,利用勾股定理得出,再由三角形的等面积法即可得.
【详解】
解:连接OF,OE,OG,
( http: / / www.21cnjy.com / )
∵AB、BC、CD分别与相切,
∴,,,且,
∴OB平分,OC平分,
∴,,
∵,
∴,
∴,
∴,
,
∴,
∴,
故选:D.
【点睛】
题目主要考查圆的切线性质,角平分线的判定和性质,平行线的性质,勾股定理等,理解题意,作出辅助线,综合运用这些知识点是解题关键.21教育名师原创作品
8、C
【分析】
根据切线长定理可得,、、,再根据∠F=60°,可知为等边三角形,,再△FDE的周长为12,可得,求得,再作,即可求解.
【详解】
解:FA、FB分别与⊙O相切于A、B两点,过点C的切线分别交FA、FB于D、E两点,
则:、、,,
∵∠F=60°,
∴为等边三角形,,
∵△FDE的周长为12,即,
∴,即,
作,如下图:
( http: / / www.21cnjy.com / )
则,,
∴,
设,则,由勾股定理可得:,
解得,,
故选C
【点睛】
此题考查了圆的有关性质,切线的性质、切线长定理,垂径定理以及等边三角形的判定与性质,解题的关键是灵活运用相关性质进行求解.【版权所有:21教育】
9、D
【分析】
根据垂径定理解答.
【详解】
解:∵AB是⊙O的直径,CD为弦,CD⊥AB于点E,
∴弧AC=弧AD,弧BC=弧BD,CE=DE,
故选:D.
【点睛】
此题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧,熟记定理是解题的关键.
10、C
【分析】
由题意根据正方形的性质得到BC弧所对的圆心角为90°,则∠BOC=90°,然后根据圆周角定理进行分析求解.
【详解】
解:连接OB、OC,如图,
( http: / / www.21cnjy.com / )
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,
∴∠BPC=∠BOC=45°.
故选:C.
【点睛】
本题考查圆周角定理和正方形的性质,确定BC弧所对的圆心角为90°是解题的关键.
二、填空题
1、45
【分析】
连接OC,OD,根据同底等高可知S△ACD=S△OCD,把阴影部分的面积转化为扇形OCD的面积,利用扇形的面积公式S=来求解.www-2-1-cnjy-com
【详解】
解:连接OC,OD,
( http: / / www.21cnjy.com / )
∵直径AB=30,
∴OC=OD=,
∴CD∥AB,
∴S△ACD=S△OCD,
∵长为6π,
∴阴影部分的面积为S阴影=S扇形OCD=,
故答案为:45π.
【点睛】
本题主要考查了扇形的面积公式,正确理解阴影部分的面积=扇形COD的面积是解题的关键.
2、24
【分析】
连接OA,过点O作OD⊥AB交AB于点C交⊙O于D,再根据勾股定理求出AC的长,进而可得出AB的长.
【详解】
解:连接OA,过点O作OD⊥AB交AB于点C交⊙O于D.
( http: / / www.21cnjy.com / )
∵OC⊥AB,
∴AC=CB,
∵OA=OD=13cm,CD=8cm,
∴OC=OD﹣CD=5(cm),
∴,
∴AB=2AC=24(cm),
故答案为:24.
【点睛】
本题主要考查垂径定理,掌握垂径定理和勾股定理是解题的关键.
3、36
【分析】
连接OA,OB,OB交AF ( http: / / www.21cnjy.com )于J.由正多边形中心角、垂径定理、圆周角定理得出∠AOB=72°,∠BOF=36°,再由等腰三角形的性质得出答案.2-1-c-n-j-y
【详解】
解:连接OA,OB,OB交AF于J.
∵五边形ABCDE是正五边形,OF⊥BC,
∴,
∴∠AOB=72°,∠BOF=∠AOB=36°,
∴∠AOF=∠AOB +∠BOF=108°,
∵OA=OF,
∴∠OAF=∠OFA==36°
( http: / / www.21cnjy.com / )
故答案为:36.
【点睛】
本题主要考查了园内正多边形中心角度数、垂径定理和圆周角定理,垂直于弦的直径平分这条弦,并且平分弦所对的两条弧,垂径定理常与勾股定理以及圆周角定理相结合来解题.正n边形的每个中心角都等于.21·cn·jy·com
4、
【分析】
先根据弧的度数与它所对应的圆心角的度数的关系,求得弧对应的圆心角的度数,再根据圆周角与圆心角的关系,则可求得.www.21-cn-jy.com
【详解】
弧的度数等于它所对应的圆心角的度数,由于弧为,所以 ,
顶点在圆上且两边都和圆相交的角叫做圆周角,而一条弧所对的圆周角等于它所对的圆心角的一半,所以:
, ,
,
故答案为:.
( http: / / www.21cnjy.com / )
【点睛】
本题考查弧、圆周角、圆心角的概念,及它们之间的关系,熟知同弧所对的圆周角等于圆心角的一半是解本题的关键.
5、
【分析】
利用勾股定理求出AC及AB的长,根据阴影面积等于求出答案.
【详解】
解:由旋转得,,=∠BAC=30°,
∵∠ABC=90°,∠BAC=30°,BC=1,
∴AC=2BC=2,AB=,,
∴阴影部分的面积=
=,
故答案为:.
. ( http: / / www.21cnjy.com / )
【点睛】
此题考查了求不规则图形的面积,正确掌握勾股定理、30度角直角三角形的性质、扇形面积计算公式及分析出阴影面积的构成特点是解题的关键.
三、解答题
1、(1)见解析;(2);(3)
【分析】
(1)过点D作DE∥AB交BC ( http: / / www.21cnjy.com )于E,由圆内接四边形对角互补可以推出∠B+∠A=180°,证得AD∥BC,则四边形ABED是平行四边形,即可得到AB=DE,∠DEC=∠B=∠C,这DE=CD=AB;
(2)连接OC,FC,设BE=CD=2x,OB=OC=OF=r,则OE=BE-BO=2x-r,EF=BF-BE=2r-2x,由垂径定理可得,∠CEB=∠CEF=∠FCB=90°,则∠FBC+∠F=∠FCE+∠F=90°,可得∠FBC=∠FCE;由勾股定理得,则,
解得,则;
(3)EF:BG=1:3,即则 解得,则,,,如图所示,以B为圆心,以BC所在的直线为x轴建立平面直角坐标系,分别过点A作AM⊥BC与M,过点G作GN⊥BC与N,连接FC,分别求出G点坐标为,C点坐标为;A点坐标为
然后求出直线CG的解析式为,直线AB的解析式为,即可得到H的坐标为(,),则.
【详解】
解:(1)如图所示,过点D作DE∥AB交BC于E,
∵四边形ABCD是圆O的圆内接四边形,
∴∠A+∠C=180°,
∵∠B=∠C,
∴∠B+∠A=180°,
∴AD∥BC,
∴四边形ABED是平行四边形,
∴AB=DE,∠DEC=∠B=∠C,
∴DE=CD=AB;
( http: / / www.21cnjy.com / )
(2)如图所示,连接OC,FC,
设BE=CD=2x,OB=OC=OF=r,则OE=BE-BO=2x-r,EF=BF-BE=2r-2x21教育网
∵CD⊥EB,BF是圆O的直径,
∴,∠CEB=∠CEF=∠FCB=90°,
∴∠FBC+∠F=∠FCE+∠F=90°,
∴∠FBC=∠FCE;
∵,
∴,
∴,
解得,
∴;
( http: / / www.21cnjy.com / )
(3)∵EF:BG=1:3,即
∴ ,即
∴,
解得,
∴,
∴,,
如图所示,以B为圆心,以BC所在的直线为x轴建立平面直角坐标系,分别过点A作AM⊥BC与M,过点G作GN⊥BC与N,连接FC,2·1·c·n·j·y
∴,
∴,,
∵,
∴,,
∴,,
∴,,
∴G点坐标为(,),C点坐标为(,0);
∵,
∴,
∵∠ABC=∠ECB,
∴,
∴,
∵,
∴,
∴,
∴,
∴A点坐标为(,)
设直线CG的解析式为,直线AB的解析式为,
∴,,
∴,,
∴直线CG的解析式为,直线AB的解析式为,
联立,
解得,
∴H的坐标为(,),
∴.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了圆内接四边 ( http: / / www.21cnjy.com )形的性质,平行四边形的性质与判定,等腰三角形的性质与判定,解直角三角形,一次函数与几何综合,垂径定理,勾股定理,两点距离公式,解题的关键在于能够正确作出辅助线,利用数形结合的思想求解.【来源:21·世纪·教育·网】
2、见解析
【分析】
连接OD,根据已知条件得到,根据等腰三角形的性质得到∠ADO=∠DAB=30°,得到∠EDA=60°,求得OD⊥DE,于是得到结论.21·世纪*教育网
【详解】
证明:连接OD,
∵,
∴.
∵,
∴.
∵,
∴.
∵,
∴.
∴.
∴.
∴.
∴.
∴DE是的切线.
( http: / / www.21cnjy.com / )
【点睛】
本题考查了切线的判定和性质,圆周角定理,正确的作出辅助线是解题的关键.
3、(1)证明见解析;(2).
【分析】
(1)连接,先根据圆周角定理可得,再根据等腰三角形的性质可得,从而可得,然后根据角的和差可得,最后根据圆的切线的判定定理即可得证;21*cnjy*com
(2)设的半径为,先在中,利用勾股定理可求出的值,从而可得的长,再根据相似三角形的判定证出,然后根据相似三角形的性质即可得.【来源:21cnj*y.co*m】
【详解】
证明:(1)如图,连接,
( http: / / www.21cnjy.com / )
是的直径,
,
,
,
,
,
,
,即,
又是的半径,
是的切线;
(2)设的半径为,则,
,
,
在中,,即,
解得,
,
在和中,,
,
,即,
解得.
【点睛】
本题考查了圆周角定理、圆的切线的判定定理、相似三角形的判定与性质等知识点,熟练掌握圆的切线的判定定理和相似三角形的判定是解题关键.
4、2+
【分析】
连接AC,CM,AB,过点C作CH⊥OA于H,设OC=a.利用勾股定理构建方程解决问题即可.
【详解】
解:连接AC,CM,AB,过点C作CH⊥OA于H,设OC=a.
( http: / / www.21cnjy.com / )
∵∠AOB=90°,
∴AB是直径,
∵A(-4,0),B(0,2),
∴,
∵∠AMC=2∠AOC=120°,
,
在Rt△COH中,,
,
在Rt△ACH中,AC2=AH2+CH2,
∴,
∴a=2+ 或2-(因为OC>OB,所以2-舍弃),
∴OC=2+,
故答案为:2+.
【点睛】
本题考查圆周角定理,勾股定理,解直角三角形等知识,解题的关键是学会利用参数构建方程解决问题.
5、(1)90°;(2)AC=,DE=1
【分析】
(1)如图,,可知.
(2),可求出的长;,,可求出的长.
【详解】
解(1)证明如图所示,连接,,
( http: / / www.21cnjy.com / )
是直径,是的切线,平分
∴,
∴
∴.
(2)解∵,
∴
∴,
∴.
在中
∵,
∴
∴,
∴.
【点睛】
本题考查了角平分线、勾股定理、等腰三角形的性质、三角形相似的判定等知识点.解题的关键在于判定三角形相似.21*cnjy*com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
