人教版九年级上册24.1.2 垂直于弦的直径 课件 (共20张PPT)
文档属性
| 名称 | 人教版九年级上册24.1.2 垂直于弦的直径 课件 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-28 07:51:27 | ||
图片预览



文档简介
(共20张PPT)
垂直于弦的直径(1)
人教九年级上册第24章
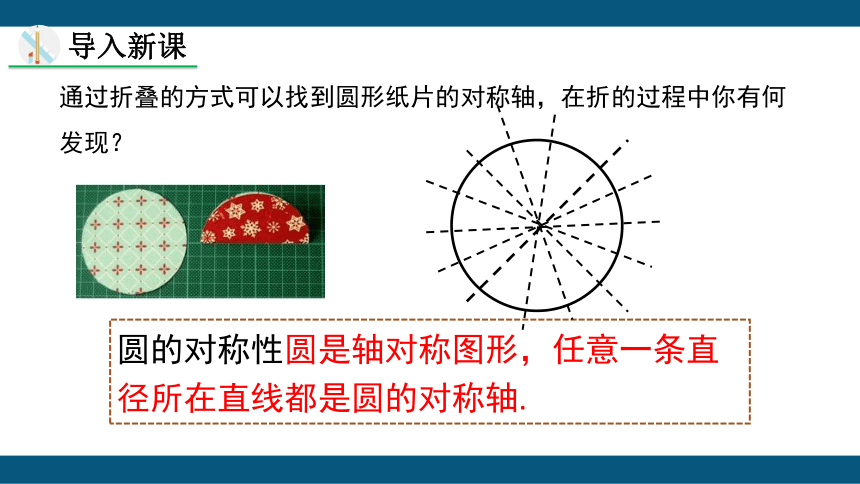
通过折叠的方式可以找到圆形纸片的对称轴,在折的过程中你有何发现?
导入新课
圆的对称性圆是轴对称图形,任意一条直径所在直线都是圆的对称轴.
●O
证明:连结OA、OB.
则OA=OB.
又∵CD⊥AB,
∴直径CD所在的直线是AB的垂直平分线.
∴对于圆上任意一点,在圆上都有关于直线CD的对称点,即⊙O关于直线CD对称.
圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
如何来证明圆是轴对称图形呢?
探究新知
探究新知
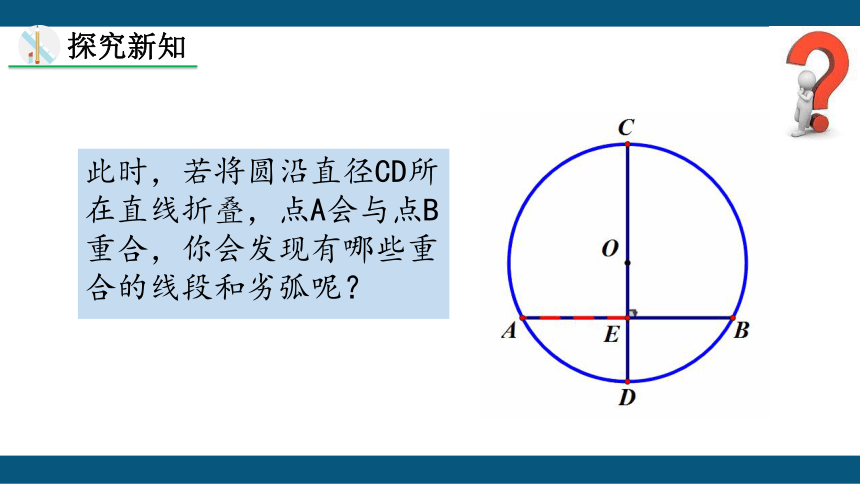
此时,若将圆沿直径CD所在直线折叠,点A会与点B重合,你会发现有哪些重合的线段和劣弧呢?
·
O
A
B
C
D
E
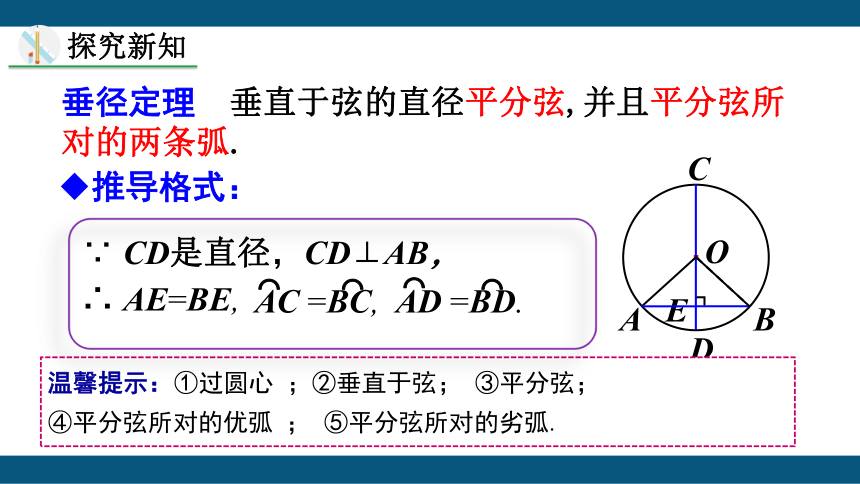
垂径定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
推导格式:
温馨提示:①过圆心 ;②垂直于弦; ③平分弦;
④平分弦所对的优弧 ; ⑤平分弦所对的劣弧.
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
探究新知
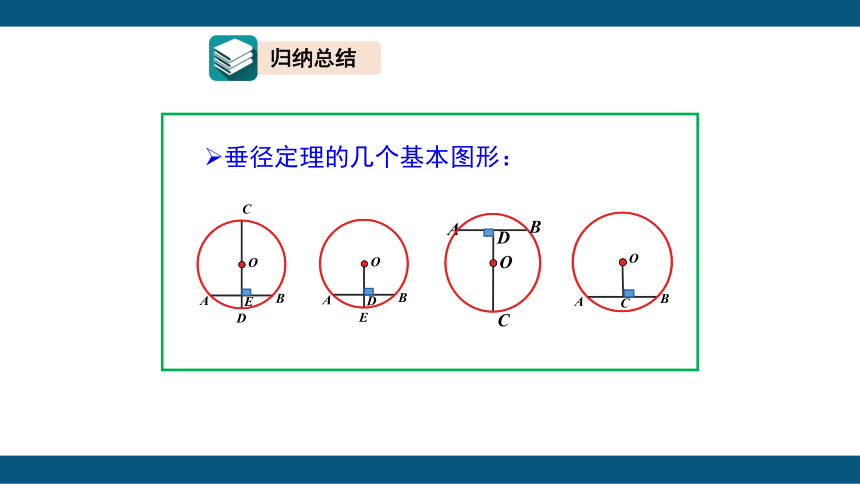
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
C
A
B
O
D
C
归纳总结
1.如图,OE⊥AB于E,若⊙O的半径为10cm,
OE=6cm,则AB= cm.
·
O
A
B
E
解:连接OA,∵ OE⊥AB,
∴ AB=2AE=16cm.
16
∴
cm.
巩固练习
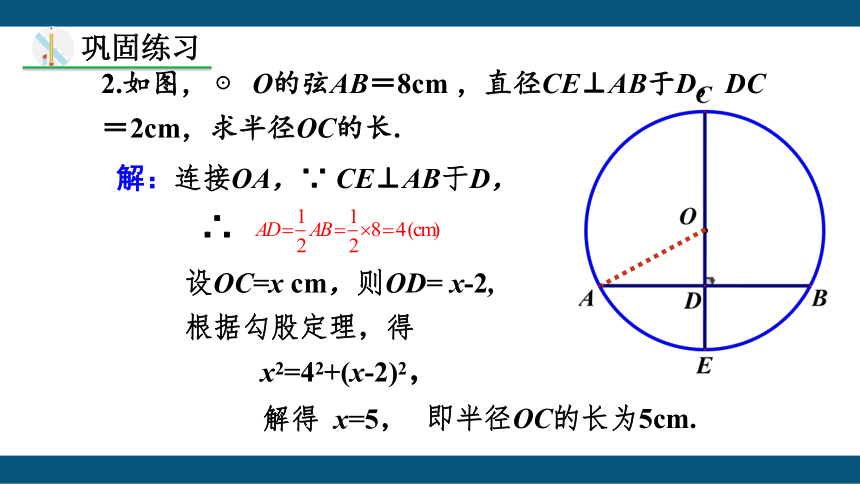
2.如图, ⊙ O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.
解:连接OA,∵ CE⊥AB于D,
∴
设OC=x cm,则OD= x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
巩固练习
归纳总结
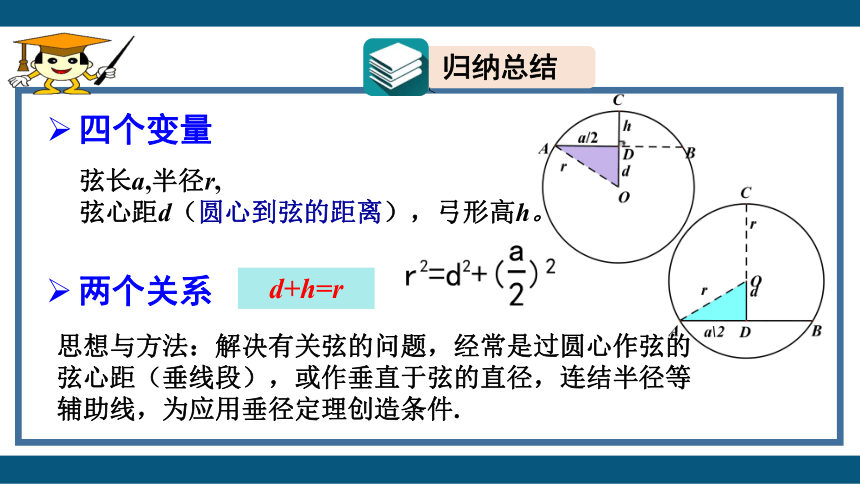
d+h=r
弦长a,半径r,
弦心距d(圆心到弦的距离),弓形高h。
两个关系
四个变量
思想与方法:解决有关弦的问题,经常是过圆心作弦的弦心距(垂线段),或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.
24.1.2 垂直于弦的直径(2)
实践探究
把手中的圆对折,重复做几次,你发现了什么
可以发现:圆是轴对称图形,
任何一条直径所在直线都是它的对称轴.
活动一
●O
实践探究(小组合作讨论)
利用手中的圆,动手折出与已知直径垂直的一条弦,并说明你折纸的理由。在折好的圆上标出如图所示的字母,讨论图中有哪些相等的量。
活动二
D
·
O
A
B
E
C
在△OAB中,
∵OA=OB
∴ △OAB是等腰三角形
又∵ AB⊥CD
∴AE=BE
归纳总结
·
O
A
B
C
D
E
由此,我们得到下面的定理:
即直径CD平分弦AB,并且平分弧AB及弧ACB
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
AE=BE,弧AD=弧BD,弧AC=弧BC
∵ CD是⊙O的直径且 CD⊥AB,
∴AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
③AE=BE,
① CD是直径
② CD⊥AB
可推得
⌒
⌒
⑤AD=BD.
⌒
⌒
④AC=BC,
几何语言表达:
两个条件
三个结论
如图,在⊙O中,弦AB的长为8 cm,圆心O到弦AB的距离为3 cm,求⊙O的半径.
·
O
A
B
E
解:
答:⊙O的半径为5 cm.
在Rt△AOE中,
巩固提高
总结:常构造以弦、半径、弦心距为边的直角三角形,利用垂径定理和直角三角形的相关知识来解决问题。
如图,连接OA,过点O作OE⊥AB于点E
已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
求证:AC=BD
拓展延伸
变式:若隐去原图中的大圆,连接OA,OB,设OA=OB,
求证:AC=BD。
拓展延伸
E
体会.分享
说出你这节课的收获和体会,让大家与你一起分享!!!
是
不是
是
不是
O
E
D
C
A
B
分析下列图形是否具备垂径定理的条件?
达标检测
3.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是 。
8cm
A
B
O
E
A
B
O
E
O
A
B
E
2. ⊙O的直径为10cm,圆心O到弦AB的 距离为3cm,则弦AB的长是 。
达标检测
C
感谢聆听,再见!
人教九年级上册第24章
垂直于弦的直径(1)
人教九年级上册第24章
通过折叠的方式可以找到圆形纸片的对称轴,在折的过程中你有何发现?
导入新课
圆的对称性圆是轴对称图形,任意一条直径所在直线都是圆的对称轴.
●O
证明:连结OA、OB.
则OA=OB.
又∵CD⊥AB,
∴直径CD所在的直线是AB的垂直平分线.
∴对于圆上任意一点,在圆上都有关于直线CD的对称点,即⊙O关于直线CD对称.
圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
如何来证明圆是轴对称图形呢?
探究新知
探究新知
此时,若将圆沿直径CD所在直线折叠,点A会与点B重合,你会发现有哪些重合的线段和劣弧呢?
·
O
A
B
C
D
E
垂径定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
推导格式:
温馨提示:①过圆心 ;②垂直于弦; ③平分弦;
④平分弦所对的优弧 ; ⑤平分弦所对的劣弧.
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
探究新知
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
C
A
B
O
D
C
归纳总结
1.如图,OE⊥AB于E,若⊙O的半径为10cm,
OE=6cm,则AB= cm.
·
O
A
B
E
解:连接OA,∵ OE⊥AB,
∴ AB=2AE=16cm.
16
∴
cm.
巩固练习
2.如图, ⊙ O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.
解:连接OA,∵ CE⊥AB于D,
∴
设OC=x cm,则OD= x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
巩固练习
归纳总结
d+h=r
弦长a,半径r,
弦心距d(圆心到弦的距离),弓形高h。
两个关系
四个变量
思想与方法:解决有关弦的问题,经常是过圆心作弦的弦心距(垂线段),或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.
24.1.2 垂直于弦的直径(2)
实践探究
把手中的圆对折,重复做几次,你发现了什么
可以发现:圆是轴对称图形,
任何一条直径所在直线都是它的对称轴.
活动一
●O
实践探究(小组合作讨论)
利用手中的圆,动手折出与已知直径垂直的一条弦,并说明你折纸的理由。在折好的圆上标出如图所示的字母,讨论图中有哪些相等的量。
活动二
D
·
O
A
B
E
C
在△OAB中,
∵OA=OB
∴ △OAB是等腰三角形
又∵ AB⊥CD
∴AE=BE
归纳总结
·
O
A
B
C
D
E
由此,我们得到下面的定理:
即直径CD平分弦AB,并且平分弧AB及弧ACB
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
AE=BE,弧AD=弧BD,弧AC=弧BC
∵ CD是⊙O的直径且 CD⊥AB,
∴AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
③AE=BE,
① CD是直径
② CD⊥AB
可推得
⌒
⌒
⑤AD=BD.
⌒
⌒
④AC=BC,
几何语言表达:
两个条件
三个结论
如图,在⊙O中,弦AB的长为8 cm,圆心O到弦AB的距离为3 cm,求⊙O的半径.
·
O
A
B
E
解:
答:⊙O的半径为5 cm.
在Rt△AOE中,
巩固提高
总结:常构造以弦、半径、弦心距为边的直角三角形,利用垂径定理和直角三角形的相关知识来解决问题。
如图,连接OA,过点O作OE⊥AB于点E
已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
求证:AC=BD
拓展延伸
变式:若隐去原图中的大圆,连接OA,OB,设OA=OB,
求证:AC=BD。
拓展延伸
E
体会.分享
说出你这节课的收获和体会,让大家与你一起分享!!!
是
不是
是
不是
O
E
D
C
A
B
分析下列图形是否具备垂径定理的条件?
达标检测
3.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是 。
8cm
A
B
O
E
A
B
O
E
O
A
B
E
2. ⊙O的直径为10cm,圆心O到弦AB的 距离为3cm,则弦AB的长是 。
达标检测
C
感谢聆听,再见!
人教九年级上册第24章
同课章节目录
