第六单元 可能性(单元测试)苏教版数学四年级上册(含解析)
文档属性
| 名称 | 第六单元 可能性(单元测试)苏教版数学四年级上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 273.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 15:32:38 | ||
图片预览




文档简介
苏教版数学四年级上册单元测试卷
第六单元 可能性
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列事件中一定不会发生的是( )。
A.抛硬币10次全部反面朝上 B.明天会下雨
C.小明昨天还是13岁,今天就14岁了 D.小李的生日是2月31号
2.在下列情况中,摸出红球可能性最小是?( )
A.8白,2红,3黑 B.5蓝,5白,2红
C.4红,4白,4黑 D.3蓝,2白,7红
3.布袋里放了5个球:〇〇〇●●,任意摸一个不放回,小明连续摸了3次都是白球。如果再摸一次,认为下面说法正确的是( )。
A.可能摸到黑球 B.一定能摸到黑球
C.摸到黑球的可能性大 D.不可能再摸到白球
4.一个正方体的6个面上分别写有1-6各数,抛一次,朝上面的数大于4的情况有( )种。
A.1 B.2 C.3
5.小军给同学打电话,忘记了号码中的最后一个数字,只记得这个数字是双数,他随意拨打,最多可能拨打( )次可以拨打成功。
A.5 B.4 C.2 D.1
6.下面有4个袋子,每个袋子中分别装有8个小球(小球除颜色外完全一样)。小聪选择其中一个袋子进行摸球试验,每次任意摸出一个球,记录结果后再放回袋子摇匀。他一共摸了40次,摸出红球29次,黄球11次。小聪选择的袋子最有可能的是( )。
A. B. C. D.
7.在不透明的袋子里装入同样数量的红球和黄球,球除颜色外完全相同,现在要使摸到红球的可能性比摸到黄球的可能性大,错误的做法是( )
A.减少红球数量 B.减少黄球数量 C.增加红球数量
8.一天早上7时正在下雨,再过17小时,( )出太阳。
A.一定 B.可能 C.不可能 D.不一定
9.口袋里有除颜色外都相同的10个球,其中5个红球,4个黄球,1个白球,从中任意摸出一个,有( )可能的结果。
A.5种 B.4种 C.3种 D.1种
10.一个口袋里装有5个红球,3个白球,1个黄球。摸到红球的可能性( )摸到白球的可能性。
A.大于 B.小于 C.等于
11.李红向下面每个靶掷一块石头(三个靶大小相等,均为等分),她最有可能击中( )靶的阴影部分。
A. B. C.
12.一个盒子里装了大小、质量完全相同的1个红球、3个黄球和5个绿球,华华伸手任意摸一个,( )。
A.模到红球的可能性最大 B.摸到黄球的可能性最小
C.摸到绿球的可能性最大 D.摸到三种颜色球的可能性一样大
13.足球比赛通过掷硬币确定谁开球,任意掷一次,下面的说法正确的是( )。
A.正面朝上的可能性大
B.反面朝上的可能性大
C.正、反面朝上的可能性一样大
14.从盒子里摸出一个球,一定摸出黑球的是( )。
A. B. C. D.
15.将2个白球和8个黑球放在一个袋子里,从口袋中不放回任意摸球,前两次摸2个白球,再摸一个球,下面说法正确的是( )。(白球与黑球仅仅只有颜色的区别)
A.一定摸到白球 B.一定摸到黑球
C.摸到黑球的可能性大 D.摸到白球的可能性大
16.下列事件中,能用“一定”描述的是( )。
A.今天是星期一,明天是星期日 B.后天刮大风 C.地球每天都在转动 D.小强比他爸爸长得高
17.下面四个袋子中装的都是一些黄球和蓝球,摸出黄球算获奖,哪个袋子获奖的可能性大。( )
A.6个黄球,3个蓝球 B.4个黄球,4个蓝球 C.3个黄球,4个蓝球 D.8个黄球,10个蓝球
18.有一种游戏的规则是:先旋转转盘的指针,如果指针箭头停在3的倍数的位置,就可以从盒子里摸出一个珠子。如果摸到黑色珠子就能得到奖品,东东玩了一次,他旋转转盘后,指针箭头所在位置和盒子里珠子的情况如下图所示。下面说法合理的是( )。
他不可能得到奖品 B.他得到奖品的可能性小
C.他得到奖品的可能性大 D.他一定可以得到奖品
19.2020年东京奥运会一共有12支女排队伍参加,用“可能”、“不可能”、和“一定”填空,填“不可能”的是( )。
A.东道主日本队( )参加
B.所有12支队伍都( )获胜
C.没有获得资格赛入场券的国家( )获胜
D.女排决赛那天( )是晴天
20.下面是同学们做摸球游戏的记录(共摸了20次)。如果再摸一次,( )。
记录 次数
白球 3
黑球 正正正 17
A.一定摸到白球 B.一定摸到黑球
C.摸到白球的可能性大 D.摸到黑球的可能性大
21.六位数密码只记得前五个数字,随便输入一个数字,( )。
A.正确的可能性大 B.错误的可能性大 C.一样大 D.无法比较
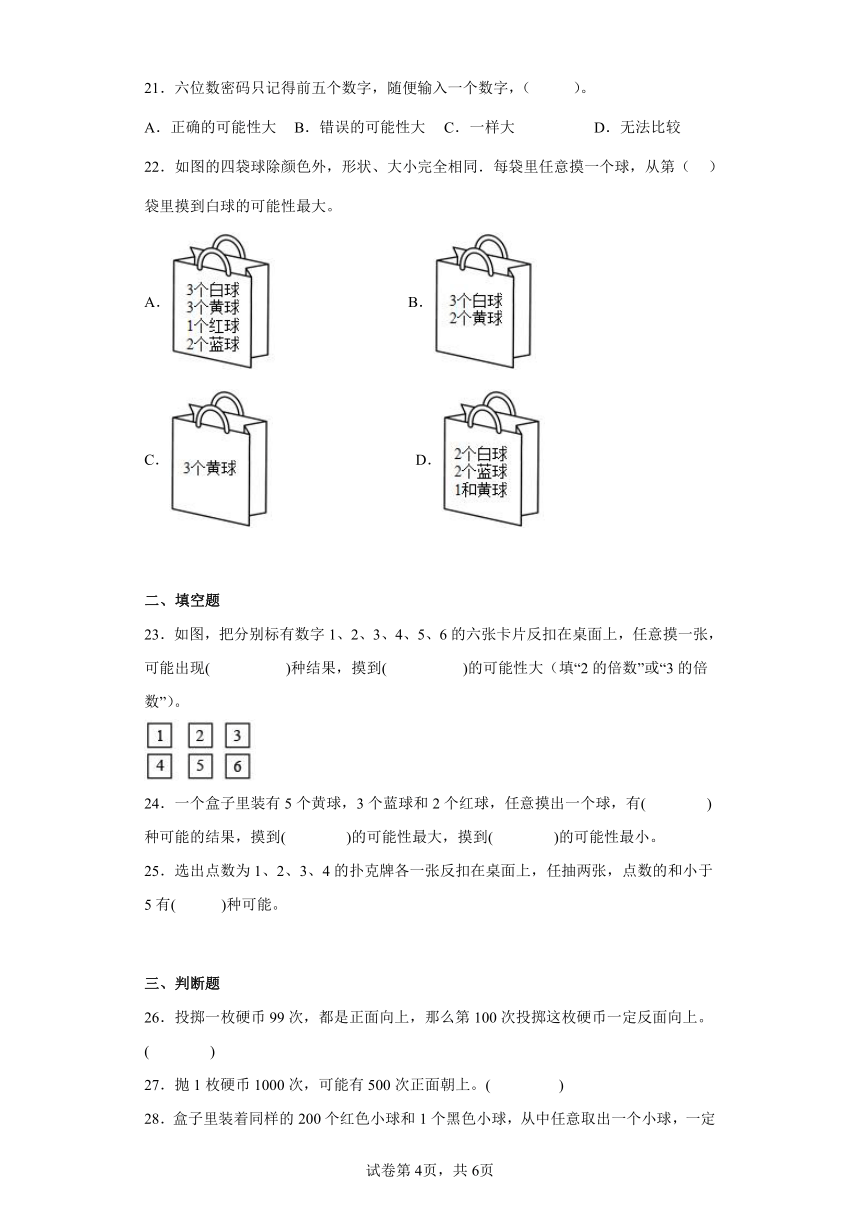
22.如图的四袋球除颜色外,形状、大小完全相同.每袋里任意摸一个球,从第( )袋里摸到白球的可能性最大。
A. B.
C. D.
二、填空题
23.如图,把分别标有数字1、2、3、4、5、6的六张卡片反扣在桌面上,任意摸一张,可能出现( )种结果,摸到( )的可能性大(填“2的倍数”或“3的倍数”)。
24.一个盒子里装有5个黄球,3个蓝球和2个红球,任意摸出一个球,有( )种可能的结果,摸到( )的可能性最大,摸到( )的可能性最小。
25.选出点数为1、2、3、4的扑克牌各一张反扣在桌面上,任抽两张,点数的和小于5有( )种可能。
三、判断题
26.投掷一枚硬币99次,都是正面向上,那么第100次投掷这枚硬币一定反面向上。( )
27.抛1枚硬币1000次,可能有500次正面朝上。( )
28.盒子里装着同样的200个红色小球和1个黑色小球,从中任意取出一个小球,一定是红色的小球。( )
29.往盒子里放两种颜色的球,共8个,任意摸1个,要使摸到绿球和蓝球的可能性相等,绿球和蓝球应各放4个。( )
30.连续抛一枚5角的硬币20次,出现正面朝上的次数一定是10。( )
31.东东抛一枚硬币,连续抛10次,一定会有5次正面朝上,5次反面朝上。( )
32.从一个纸箱里摸球,每次摸一个后放回,摇匀再摸。一共摸了40次,结果红球摸到了32次,白球摸到了8次,那么原来纸箱里红球的数量可能比白球多。( )
四、连线题
33.连线。
五、作图题
34.洋洋和东东做一个摸球游戏。在一个不透明的袋中放10个同样的小球(只有红、黑两种颜色),每次摸一个,摸后放回,每人摸20次。摸到红球的次数多,算洋洋赢;摸到黑球的次数多,算东东赢。
(1)如果希望两人打平手,袋中应该怎样放10个球,涂出来。
(2)如果希望洋洋赢,袋中应该放怎样的10个球,涂出来。
(3)如果希望东东赢,袋中应该放怎样的10个球,涂出来。
六、解答题
35.幸福超市准备在2021年春节期间开展商品促销活动,每位顾客买商品满500元就可抽一次奖。在一个纸箱里任意摸一个球,摸出红球是一等奖,摸出黄球是二等奖,摸出绿球是三等奖,摸出白球不得奖。(规定纸箱里放100个球,而且四种颜色的球都要放)
(1)如果你是超市经理,准备怎样安排纸箱里的球?
(2)如果你是顾客,希望怎样安排纸箱里的球?
36.从4张数字卡片 、 、 、 中任意取出3张摆成一个三位数,摆成末尾有0的数的可能性大还是摆成中间有0的数的可能性大?
37.在箱子里放入红、黄、蓝三种颜色的球共12个,请根据方案确定它们的个数。
方案一:摸到三种颜色的球的可能性同样大。
方案二:摸到三种颜色的球各不相同。
方案三:摸到红球的可能性最大,摸到黄球和蓝球的可能性相同。
方案四:摸到黄球的可能性最大,摸到红球的可能性较小,不可能摸到蓝球。
红球 黄球 蓝球
方案1
方案2
方案3
方案4
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,结合实际生活,按要求选择即可。
【详解】A.抛硬币10次全部反面朝上,是有可能,属于不确定事件,所以不能用“一定”描述,故选项错误;
B.明天会下雨,这是随机事件,可能发生,所以不能用“一定”描述,故选项错误;
C.小明昨天还是13岁,今天就14岁了,说明小明昨天生日,这是可能性事件,所以不能用“一定”描述,故选项错误;
D.小李的生日是2月31号,2月最多闰年29天,不会出现31号,属于确定事件中的不可能事件,一定不会发生,所以只能用“一定”描述,故选项正确。
故答案为:D
【点睛】此题主要考查了事件的确定性和不确定性,要熟练掌握。
2.A
【分析】红球在总球数里数量越多,摸出的可能性越大;数量越少,磨出的可能性越小;据此依次分析即可解答。
【详解】A.红球2个,总数13个;
B.红球2个,总数12个;
C.红球4个,总数12个;
D.红球7个,总数13个;
BCD的总数是12,所以选项BCD中,选项B红色少,所以可能性最小,为2÷12,但是选项A的总数是13个,可能性是2÷13,而2÷13<2÷12
故答案为:A
【点睛】本题考查的是可能性大小的比较,根据方法解题,依次分析。
3.B
【分析】因为袋子里放了5个球,有黑球,也有白球,其中黑球有2个,白球有3个,任意摸一个不放回,小明连续摸了3次都是白球,那么剩下的球都是黑球了,再摸一次,摸到黑球的概率就是1了,据此选择解答即可。
【详解】布袋里黑球和白球都有,任意摸一个再放回,小明连续摸了3次都是白球后,袋子里只剩下黑球,所以再摸一次只能摸到黑球。
故答案为:B
【点睛】注意关键字“不放回”,此时袋子里只剩下黑球,所以一定摸到黑球。
4.B
【分析】向上抛一次,可能出现1、2、3、4、5、6这6种情况,大于4的数只有5和6两个,所以抛一次,朝上面的数大于4的情况有2种。
【详解】根据分析可得,抛一次,朝上面的数大于4的情况有2种。
故答案为:B
【点睛】本题考查可能性,解答本题的关键是找到所有可能发生的情况。
5.A
【分析】0~9这10个数字中的双数,分别是0、2、4、6、8,共5种情况,0也是双数(偶数)。所以他随意拨打,最多可能拨打5次可以拨打成功。
【详解】根据分析可知,他随意拨打,最多可能拨打5次可以拨打成功。
故答案为:A
【点睛】本题要注意0也是偶数,这是解答本题的关键。
6.B
【分析】根据题意可知,袋子中装的红球一定比黄球多,据此解答即可。
【详解】选项A和D是只有一种颜色球,错误;选项C袋子中的红球和黄球各占一半,摸出的可能性也是比较接近的;所以选项B符合题意。
故答案为:B。
【点睛】本题考查可能性的大小,解答本题的关键是掌握可能性的大小是由出现次数的多少来决定。
7.A
【详解】略
8.C
【分析】早上7时,经过17小时后是24时,这时是晚上,根据常识可知,晚上不可能有太阳,据此即可解答。
【详解】根据分析可知,一天早上7时正在下雨,再过17小时,不可能出太阳。
故答案为:C
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
9.C
【解析】口袋里有除颜色外都相同的10个球,其中5个红球,4个黄球,1个白球,共三种颜色的球,从中任意摸出一个,有3可能的结果:可能是红球,也可能是黄球,也可能是白球,属于不确定事件中的可能性事件;由此解答即可。
【详解】口袋里有除颜色外都相同的10个球,其中5个红球,4个黄球,1个白球,从中任意摸出一个,有3种可能的结果,属于不确定事件中的可能性事件;
故答案为:C
【点睛】明确有几种颜色的球,任意摸出一个,就会有几种结果,是解答此题的关键。
10.A
【分析】根据可能性大小计算公式计算比较即可。
【详解】红球可能性:5÷(5+3+1)=
白球的可能性:3÷(5+3+1)==
>
故答案为:A
【点睛】本题主要考查可能性大小的判断,解答此题应根据可能性的求法:即求一个数是另一个数的几分之几用除法解答,进而得出结论。
11.A
【分析】用分数表示出三个图形的阴影部分,比较分数的大小,阴影部分越大,击中的可能性越大。
【详解】A.阴影部分用分数表示是;
B.阴影部分用分数表示是;
C.阴影部分用分数表示是=;
=、=、=,最大的是A。
故答案为:A
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。当条件对事件的发生有利时,发生的可能性就大一些。
12.C
【解析】根据根据可能性大小的判断方法:不求准确值时,根据物体的数量判断可能性的大小,数量多的可能性大,盒子里有1个红球、3个黄球和5个绿球,3种球中绿球的数量最多,所以摸到绿球的可能性大;红球最少,所以摸到红球的可能性最小;据此解答即可。
【详解】因为5>3>1,所以摸绿球的可能性最大,摸出红球的可能性最小;
故答案为:C
【点睛】解答此题应根据判断可能性大小的方法:不求准确值时,根据物体的数量判断可能性的大小,数量多的可能性大。
13.C
【分析】根据常识知识可知,每枚硬币都有正反两个面,任意掷一次,正面朝上和反面朝上的可能性是一样的,据此即可解答。
【详解】根据分析可知,任意掷一次,正、反面朝上的可能性一样大。
故答案为:C
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
14.A
【解析】要想一定是黑球,则所有球的颜色都是黑色,据此解答。
【详解】要想一定是黑球,则所有球的颜色都是黑色,因为A盒子中的球都是黑球,所以,在A盒子里一定摸到黑球。
故答案为:A
【点睛】此题主要考查根据可能性的大小涂色,总数相同的情况下,数量多的可能性大,数量少的可能性小,一个也没有的就不可能。
15.B
【分析】根据袋子里只有2个白球,从口袋中不放回,任意摸球,前两次摸2个白球,可以直接判断袋子里已经没有白球了,由此得解。
【详解】根据上面的分析可知:将2个白球和8个黑球放在一个袋子里,从口袋中不放回任意摸球,前两次摸2个白球,再摸一个球一定摸到黑球。
故答案为:B
【点睛】解答此类问题的关键是弄清题意,不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小。
16.C
【分析】在一定的条件下,一些事件的结果是可以预知的,具有确定性;一些事件的结果是不可能预知的,具有不确定性。确定的事件用“一定”“不可能”来描述,不确定的事件用“可能”来描述。
【详解】A.今天是星期一,明天是星期日,这是不可能事件,所以不能用“一定”描述,故选项错误;
B.后天刮大风,这是随机事件,可能发生,所以不能用“一定”描述,故选项错误;
C.地球每天都在转动,这是确定事件。所以能用“一定”描述,故选项正确;
D.小强比他爸爸长得高,这是随机事件,可能发生,所以不能用“一定”描述,故选项错误。
故答案为:C
【点睛】能够对确定事件和不确定事件进行区分。
17.A
【解析】四个袋子中装的都是一些黄球和蓝球,摸出黄球算获奖,A袋中6个黄球,3个蓝球,黄球的个数>蓝球的个数,摸出黄球的可能性大;B袋中黄球、篮球各4个,摸到黄球、蓝球的可能性相等;C袋中3个黄球、4个蓝球,黄球的个数<蓝球的个数,摸到蓝球的可能性大;D袋中8个黄球,10个蓝球,黄球的个数<蓝球的个数,摸到蓝球的可能性大。
【详解】A.6个黄球,3个蓝球,黄球的个数>蓝球的个数,摸出黄球的可能性大,即获奖的可能性大;
B.4个黄球,4个蓝球,黄球的个数=蓝球的个数,摸出黄球、蓝球的可能性,即获奖与不获奖可能性相等;
C.3个黄球,4个蓝球,黄球的个数<蓝球的个数,摸出黄球的可能性大小,即获奖的可能性小;
D.8个黄球,10个蓝球,黄球的个数<蓝球的个数,摸出黄球的可能性大小,即获奖的可能性小。
故答案为:A
【点睛】袋中哪种颜色球的个数多,摸到的可能性就大,反之,摸到的可能性就小。
18.B
【分析】9是3的倍数,可以从盒子里摸出一个珠子;盒子里白色珠子有7颗,黑色珠子有3颗,所以得到奖品的可能性是,得不到奖品的可能性是;据此解答。
【详解】选项A,得到奖品的可能性是,该选项不正确;
选项B,得到奖品的可能性是,得不到奖品的可能性是,<,该选项正确;
选项C,得到奖品的可能性是,得不到奖品的可能性是,<,该选项不正确;
选项D,得到奖品的可能性是,不一定得到奖品,该选项不正确;
故答案为:B
【点睛】本题考查可能性大小的实际应用,解题的关键是理解“可能”与“一定”的区别。
19.C
【分析】“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,结合实际生活,按要求进行判断即可。
【详解】A.东道主日本队可能参加;
B.所有12支队伍都可能获胜;
C.没有获得资格赛入场券的国家不可能获胜;
D.女排决赛那天可能是晴天。
故答案为:C
【点睛】此题考查的是事件的确定性和不确定性,应明确事件的确定性和不确定性,并能结合实际进行正确判断。
20.D
【分析】根据记录可知,摸到黑球的次数要大于摸到白球的次数,则再摸一次,可能摸到黑球,也可能摸到白球,摸到黑球的可能性较大。
【详解】如果再摸一次,摸到黑球的可能性大。
故答案为:D
【点睛】可能性的大小与它在总数中所占数量的多少有关。
21.B
【分析】此题主要考查了可能性的大小,因为是六位数密码只记得前五个数字,个位数字是0~9中间的任意一个,所以随便输入一个数字,错误的可能性大。
【详解】根据分析:
六位数密码只记得前五个数字,随便输入一个数字,错误的可能性大。
故答案为:B
【点睛】此题考查了对可能性的求法的运用。
22.B
【详解】略
23. 6 2的倍数
【分析】有六张不同的卡片,所以任意摸一张有1、2、3、4、5、6共6种不同的结果,2的倍数有2、4、6共3个数字,3的倍数有3、6共2个数字,所以摸到2的倍数的可能性大,据此即可解答。
【详解】根据分析可知,把分别标有数字1、2、3、4、5、6的六张卡片反扣在桌面上,任意摸一张,可能出现6种结果,摸到2的倍数的可能性大(填“2的倍数”或“3的倍数”)。
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
24. 3 黄 红
【分析】可以直接根据球的数量的多少来判断,数量多的摸到的可能性就大,数量少的摸到的可能性就小。因为盒子里黄球的个数最多,所以摸到黄球的可能性最大;盒子里红球的个数最少,所以摸到红球的可能性就最小;据此解答即可。
【详解】一个盒子里装有5个黄球,3个蓝球和2个红球,从盒子中任意摸出一个球,有3种可能的结果,摸到黄球可能性最大,摸到红球的可能性最小。
【点睛】解决此题关键是如果不需要准确地计算可能性的大小时,可以根据各种球个数的多少,直接判断可能性的大小。
25.2
【分析】两两组合,求出和小于5的一共有几组即可。
【详解】点数的和的所有可能的情况为:
1+2=3,1+3=4,1+4=5,2+3=5,2+4=6,3+4=7,
所以任抽两张,点数的和小于5有2种可能。
【点睛】列举搭配的时候按顺序搭配,可以避免重复。
26.×
【分析】判断正面朝上的可能性,要看一共有几种可能发生的情况,用1除以总数,即可得到发生的可能性。
【详解】因为硬币有两个面:一个正面、一个反面,所以,可能发生的情况只有两种,反面朝上与反面朝上的可能性都是:
所以投掷一枚硬币99次,都是正面向上,那么第100次投掷这枚硬币一定反面向上,说法错误。
故答案为:×
【点睛】投硬币事件是不确定性事件,每次投掷出现正面或反面朝上的可能性大小都是一样的,跟投掷次数无关,所以第100次可能正面朝上,可能反面朝上。
27.√
【分析】硬币只有正、反两面,抛出硬币,正面朝上的可能性是,属于不确定事件中的可能性事件,而不是一定是,由此判断即可。
【详解】根据题干分析可得:一个硬币抛1000次,正面朝上的可能性是,正面朝上可能是500次,属于不确定事件中的可能性事件,而不是一定为500次,原题说法正确。
故答案为:√
28.×
【详解】略
29.√
【分析】哪种颜色的球的数量越多,摸到的可能性就越大,所以要使任意摸一个,摸出两种颜色球的可能性相同,可得两种颜色的球的数量相等,据此求出有多少个绿球、蓝球,从而判断。
【详解】要使任意摸一个,摸出两种颜色球的可能性相同,可得两种颜色的球的数量相等,所以两种颜色的球的数量都是:
8÷2=4(个)
原题说法正确。
故答案为:√。
【点睛】解答此类问题的关键是需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答。
30.×
【分析】抛一枚5角的硬币,出现正面朝上和反面朝上的可能性是一样的,但并不是说正反面朝上的次数一定一样多,所以连续抛一枚5角的硬币20次,出现正面朝上的次数可能是10,也可能多于10,也可能少于10。
【详解】连续抛一枚5角的硬币20次,出现正面朝上的次数不一定是10,所以判断错误。
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
31.×
【分析】抛硬币时正面朝上和反面朝上的可能性是相等的,但在实际操作中,有可能两面朝上的次数各5次,也有可能出现正面朝上的次数多一些,反面朝上的次数少些。
【详解】东东抛一枚硬币,连续抛10次,有可能两面朝上的次数各5次,也可能出现一面朝上的次数多一些,而另一面朝上的次数少些。
故答案为:×
【点睛】本题考查可能性,解答本题的关键是理解抛硬币正面朝上和反面朝上的可能性是相等的。
32.√
【分析】根据摸到各种颜色的球的次数及摸球的总次数,可以推测各种球个数可能的多少,但是并不能肯定,据此判断。
【详解】32>8
红球的个数比白球可能多。说法正确;
故答案为:√
【点睛】本题主要考查可能性的大小,关键根据各种颜色的球出现的次数多少,推测其个数的多少。
33.见详解
【分析】只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等,如果没有包含该情况就不可能发生,如果包含的全部是该情况就一定能发生。
【详解】
【点睛】本题主要考查学生对可能性大小比较知识的掌握和灵活运用。
34.(1)
(2)(答案不唯一)
(3)(答案不唯一)
【分析】(1)根据游戏规则,如果希望两人打平手,红、黑两种颜色的球各放5个;
(2)根据游戏规则,如果希望洋洋赢,红球的个数应大于黑球的个数;
(3)根据游戏规则,如果希望东东赢,红球的个数应小于黑球的个数。
【详解】(1)
(2)(答案不唯一)
(3)(答案不唯一)
【点睛】不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小是解答本题的关键。
35.见详解
【分析】(1)站在超市经理的立场上考虑:一等奖的数量最少,所以放的红球数量最少;二等奖的数量比一等奖稍多,所以黄球的数量要比红球的数量稍多,三等奖的数量更多一些,所以绿球的数量比黄球再多一些;不得奖的数量最多,所以白球的数量最多。
(2)站在顾客立场上考虑:一等奖的数量最多,所以放的红球数量最多;二等奖的数量比一等奖稍少,所以黄球的数量要比红球的数量稍少,三等奖的数量更少一些,所以绿球的数量比黄球再少一些;不得奖的数量最少,所以白球的数量最少。
【详解】(1)如果我是超市经理,安排红球个数最少,黄球的数量要比红球的数量稍多,绿球的数量比黄球再多一些;白球的数量最多。
(2)如果我是顾客,放的红球数量最多;黄球的数量要比红球的数量稍少,绿球的数量比黄球再少一些;白球的数量最少。
【点睛】可能性的大小与它在总数中所占数量的多少有关。在总数中占的数量越多,摸到的可能性就越大,占的数量越少,摸到的可能性就越小。
36.可能性相同
【分析】0、6、1、8任意取三张摆成一个三位数,一共有18种不同的情况,其中末尾有0的数有:180、810、160、610、860、680,共6个。中间有0的数有:108、801、106、601、806、608,共6个。没有0的数有:618、681、168、186、861、816,共6个。据此解答即可。
【详解】从4张数字卡片 、 、 、 中任意取出3张摆成一个三位数,共18种情况。其中摆成末尾有0的数有6个,摆成中间有0的数有6个,二者可能性相同。
【点睛】可能性的大小与它在总数中所占数量的多少有关。
37.见解析
【分析】方案一:摸到三种颜色的球的可能性同样大,只要让三种颜色的球的个数相等即可;
方案二:摸到三种颜色的球各不相同,只要让三种颜色球的个数都不相同即可;
方案三:摸到红球的可能性最大,摸到黄球和蓝球的可能性相同,只要让红球最多,黄球和蓝球的个数相等即可;
方案四:摸到黄球的可能性最大,摸到红球的可能性较小,不可能摸到蓝球,只要黄球个数最多,剩下的都是红球,没有蓝球即可。
【详解】如图:
红球 黄球 蓝球
方案1 4个 4个 4个
方案2 3个 4个 5个
方案3 6个 3个 3个
方案4 1个 11个 0个
【点睛】解答此题应结合题意,根据可能性的大小把12个球按颜色进行分配即可。
答案第1页,共2页
答案第1页,共2页
第六单元 可能性
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列事件中一定不会发生的是( )。
A.抛硬币10次全部反面朝上 B.明天会下雨
C.小明昨天还是13岁,今天就14岁了 D.小李的生日是2月31号
2.在下列情况中,摸出红球可能性最小是?( )
A.8白,2红,3黑 B.5蓝,5白,2红
C.4红,4白,4黑 D.3蓝,2白,7红
3.布袋里放了5个球:〇〇〇●●,任意摸一个不放回,小明连续摸了3次都是白球。如果再摸一次,认为下面说法正确的是( )。
A.可能摸到黑球 B.一定能摸到黑球
C.摸到黑球的可能性大 D.不可能再摸到白球
4.一个正方体的6个面上分别写有1-6各数,抛一次,朝上面的数大于4的情况有( )种。
A.1 B.2 C.3
5.小军给同学打电话,忘记了号码中的最后一个数字,只记得这个数字是双数,他随意拨打,最多可能拨打( )次可以拨打成功。
A.5 B.4 C.2 D.1
6.下面有4个袋子,每个袋子中分别装有8个小球(小球除颜色外完全一样)。小聪选择其中一个袋子进行摸球试验,每次任意摸出一个球,记录结果后再放回袋子摇匀。他一共摸了40次,摸出红球29次,黄球11次。小聪选择的袋子最有可能的是( )。
A. B. C. D.
7.在不透明的袋子里装入同样数量的红球和黄球,球除颜色外完全相同,现在要使摸到红球的可能性比摸到黄球的可能性大,错误的做法是( )
A.减少红球数量 B.减少黄球数量 C.增加红球数量
8.一天早上7时正在下雨,再过17小时,( )出太阳。
A.一定 B.可能 C.不可能 D.不一定
9.口袋里有除颜色外都相同的10个球,其中5个红球,4个黄球,1个白球,从中任意摸出一个,有( )可能的结果。
A.5种 B.4种 C.3种 D.1种
10.一个口袋里装有5个红球,3个白球,1个黄球。摸到红球的可能性( )摸到白球的可能性。
A.大于 B.小于 C.等于
11.李红向下面每个靶掷一块石头(三个靶大小相等,均为等分),她最有可能击中( )靶的阴影部分。
A. B. C.
12.一个盒子里装了大小、质量完全相同的1个红球、3个黄球和5个绿球,华华伸手任意摸一个,( )。
A.模到红球的可能性最大 B.摸到黄球的可能性最小
C.摸到绿球的可能性最大 D.摸到三种颜色球的可能性一样大
13.足球比赛通过掷硬币确定谁开球,任意掷一次,下面的说法正确的是( )。
A.正面朝上的可能性大
B.反面朝上的可能性大
C.正、反面朝上的可能性一样大
14.从盒子里摸出一个球,一定摸出黑球的是( )。
A. B. C. D.
15.将2个白球和8个黑球放在一个袋子里,从口袋中不放回任意摸球,前两次摸2个白球,再摸一个球,下面说法正确的是( )。(白球与黑球仅仅只有颜色的区别)
A.一定摸到白球 B.一定摸到黑球
C.摸到黑球的可能性大 D.摸到白球的可能性大
16.下列事件中,能用“一定”描述的是( )。
A.今天是星期一,明天是星期日 B.后天刮大风 C.地球每天都在转动 D.小强比他爸爸长得高
17.下面四个袋子中装的都是一些黄球和蓝球,摸出黄球算获奖,哪个袋子获奖的可能性大。( )
A.6个黄球,3个蓝球 B.4个黄球,4个蓝球 C.3个黄球,4个蓝球 D.8个黄球,10个蓝球
18.有一种游戏的规则是:先旋转转盘的指针,如果指针箭头停在3的倍数的位置,就可以从盒子里摸出一个珠子。如果摸到黑色珠子就能得到奖品,东东玩了一次,他旋转转盘后,指针箭头所在位置和盒子里珠子的情况如下图所示。下面说法合理的是( )。
他不可能得到奖品 B.他得到奖品的可能性小
C.他得到奖品的可能性大 D.他一定可以得到奖品
19.2020年东京奥运会一共有12支女排队伍参加,用“可能”、“不可能”、和“一定”填空,填“不可能”的是( )。
A.东道主日本队( )参加
B.所有12支队伍都( )获胜
C.没有获得资格赛入场券的国家( )获胜
D.女排决赛那天( )是晴天
20.下面是同学们做摸球游戏的记录(共摸了20次)。如果再摸一次,( )。
记录 次数
白球 3
黑球 正正正 17
A.一定摸到白球 B.一定摸到黑球
C.摸到白球的可能性大 D.摸到黑球的可能性大
21.六位数密码只记得前五个数字,随便输入一个数字,( )。
A.正确的可能性大 B.错误的可能性大 C.一样大 D.无法比较
22.如图的四袋球除颜色外,形状、大小完全相同.每袋里任意摸一个球,从第( )袋里摸到白球的可能性最大。
A. B.
C. D.
二、填空题
23.如图,把分别标有数字1、2、3、4、5、6的六张卡片反扣在桌面上,任意摸一张,可能出现( )种结果,摸到( )的可能性大(填“2的倍数”或“3的倍数”)。
24.一个盒子里装有5个黄球,3个蓝球和2个红球,任意摸出一个球,有( )种可能的结果,摸到( )的可能性最大,摸到( )的可能性最小。
25.选出点数为1、2、3、4的扑克牌各一张反扣在桌面上,任抽两张,点数的和小于5有( )种可能。
三、判断题
26.投掷一枚硬币99次,都是正面向上,那么第100次投掷这枚硬币一定反面向上。( )
27.抛1枚硬币1000次,可能有500次正面朝上。( )
28.盒子里装着同样的200个红色小球和1个黑色小球,从中任意取出一个小球,一定是红色的小球。( )
29.往盒子里放两种颜色的球,共8个,任意摸1个,要使摸到绿球和蓝球的可能性相等,绿球和蓝球应各放4个。( )
30.连续抛一枚5角的硬币20次,出现正面朝上的次数一定是10。( )
31.东东抛一枚硬币,连续抛10次,一定会有5次正面朝上,5次反面朝上。( )
32.从一个纸箱里摸球,每次摸一个后放回,摇匀再摸。一共摸了40次,结果红球摸到了32次,白球摸到了8次,那么原来纸箱里红球的数量可能比白球多。( )
四、连线题
33.连线。
五、作图题
34.洋洋和东东做一个摸球游戏。在一个不透明的袋中放10个同样的小球(只有红、黑两种颜色),每次摸一个,摸后放回,每人摸20次。摸到红球的次数多,算洋洋赢;摸到黑球的次数多,算东东赢。
(1)如果希望两人打平手,袋中应该怎样放10个球,涂出来。
(2)如果希望洋洋赢,袋中应该放怎样的10个球,涂出来。
(3)如果希望东东赢,袋中应该放怎样的10个球,涂出来。
六、解答题
35.幸福超市准备在2021年春节期间开展商品促销活动,每位顾客买商品满500元就可抽一次奖。在一个纸箱里任意摸一个球,摸出红球是一等奖,摸出黄球是二等奖,摸出绿球是三等奖,摸出白球不得奖。(规定纸箱里放100个球,而且四种颜色的球都要放)
(1)如果你是超市经理,准备怎样安排纸箱里的球?
(2)如果你是顾客,希望怎样安排纸箱里的球?
36.从4张数字卡片 、 、 、 中任意取出3张摆成一个三位数,摆成末尾有0的数的可能性大还是摆成中间有0的数的可能性大?
37.在箱子里放入红、黄、蓝三种颜色的球共12个,请根据方案确定它们的个数。
方案一:摸到三种颜色的球的可能性同样大。
方案二:摸到三种颜色的球各不相同。
方案三:摸到红球的可能性最大,摸到黄球和蓝球的可能性相同。
方案四:摸到黄球的可能性最大,摸到红球的可能性较小,不可能摸到蓝球。
红球 黄球 蓝球
方案1
方案2
方案3
方案4
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,结合实际生活,按要求选择即可。
【详解】A.抛硬币10次全部反面朝上,是有可能,属于不确定事件,所以不能用“一定”描述,故选项错误;
B.明天会下雨,这是随机事件,可能发生,所以不能用“一定”描述,故选项错误;
C.小明昨天还是13岁,今天就14岁了,说明小明昨天生日,这是可能性事件,所以不能用“一定”描述,故选项错误;
D.小李的生日是2月31号,2月最多闰年29天,不会出现31号,属于确定事件中的不可能事件,一定不会发生,所以只能用“一定”描述,故选项正确。
故答案为:D
【点睛】此题主要考查了事件的确定性和不确定性,要熟练掌握。
2.A
【分析】红球在总球数里数量越多,摸出的可能性越大;数量越少,磨出的可能性越小;据此依次分析即可解答。
【详解】A.红球2个,总数13个;
B.红球2个,总数12个;
C.红球4个,总数12个;
D.红球7个,总数13个;
BCD的总数是12,所以选项BCD中,选项B红色少,所以可能性最小,为2÷12,但是选项A的总数是13个,可能性是2÷13,而2÷13<2÷12
故答案为:A
【点睛】本题考查的是可能性大小的比较,根据方法解题,依次分析。
3.B
【分析】因为袋子里放了5个球,有黑球,也有白球,其中黑球有2个,白球有3个,任意摸一个不放回,小明连续摸了3次都是白球,那么剩下的球都是黑球了,再摸一次,摸到黑球的概率就是1了,据此选择解答即可。
【详解】布袋里黑球和白球都有,任意摸一个再放回,小明连续摸了3次都是白球后,袋子里只剩下黑球,所以再摸一次只能摸到黑球。
故答案为:B
【点睛】注意关键字“不放回”,此时袋子里只剩下黑球,所以一定摸到黑球。
4.B
【分析】向上抛一次,可能出现1、2、3、4、5、6这6种情况,大于4的数只有5和6两个,所以抛一次,朝上面的数大于4的情况有2种。
【详解】根据分析可得,抛一次,朝上面的数大于4的情况有2种。
故答案为:B
【点睛】本题考查可能性,解答本题的关键是找到所有可能发生的情况。
5.A
【分析】0~9这10个数字中的双数,分别是0、2、4、6、8,共5种情况,0也是双数(偶数)。所以他随意拨打,最多可能拨打5次可以拨打成功。
【详解】根据分析可知,他随意拨打,最多可能拨打5次可以拨打成功。
故答案为:A
【点睛】本题要注意0也是偶数,这是解答本题的关键。
6.B
【分析】根据题意可知,袋子中装的红球一定比黄球多,据此解答即可。
【详解】选项A和D是只有一种颜色球,错误;选项C袋子中的红球和黄球各占一半,摸出的可能性也是比较接近的;所以选项B符合题意。
故答案为:B。
【点睛】本题考查可能性的大小,解答本题的关键是掌握可能性的大小是由出现次数的多少来决定。
7.A
【详解】略
8.C
【分析】早上7时,经过17小时后是24时,这时是晚上,根据常识可知,晚上不可能有太阳,据此即可解答。
【详解】根据分析可知,一天早上7时正在下雨,再过17小时,不可能出太阳。
故答案为:C
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
9.C
【解析】口袋里有除颜色外都相同的10个球,其中5个红球,4个黄球,1个白球,共三种颜色的球,从中任意摸出一个,有3可能的结果:可能是红球,也可能是黄球,也可能是白球,属于不确定事件中的可能性事件;由此解答即可。
【详解】口袋里有除颜色外都相同的10个球,其中5个红球,4个黄球,1个白球,从中任意摸出一个,有3种可能的结果,属于不确定事件中的可能性事件;
故答案为:C
【点睛】明确有几种颜色的球,任意摸出一个,就会有几种结果,是解答此题的关键。
10.A
【分析】根据可能性大小计算公式计算比较即可。
【详解】红球可能性:5÷(5+3+1)=
白球的可能性:3÷(5+3+1)==
>
故答案为:A
【点睛】本题主要考查可能性大小的判断,解答此题应根据可能性的求法:即求一个数是另一个数的几分之几用除法解答,进而得出结论。
11.A
【分析】用分数表示出三个图形的阴影部分,比较分数的大小,阴影部分越大,击中的可能性越大。
【详解】A.阴影部分用分数表示是;
B.阴影部分用分数表示是;
C.阴影部分用分数表示是=;
=、=、=,最大的是A。
故答案为:A
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。当条件对事件的发生有利时,发生的可能性就大一些。
12.C
【解析】根据根据可能性大小的判断方法:不求准确值时,根据物体的数量判断可能性的大小,数量多的可能性大,盒子里有1个红球、3个黄球和5个绿球,3种球中绿球的数量最多,所以摸到绿球的可能性大;红球最少,所以摸到红球的可能性最小;据此解答即可。
【详解】因为5>3>1,所以摸绿球的可能性最大,摸出红球的可能性最小;
故答案为:C
【点睛】解答此题应根据判断可能性大小的方法:不求准确值时,根据物体的数量判断可能性的大小,数量多的可能性大。
13.C
【分析】根据常识知识可知,每枚硬币都有正反两个面,任意掷一次,正面朝上和反面朝上的可能性是一样的,据此即可解答。
【详解】根据分析可知,任意掷一次,正、反面朝上的可能性一样大。
故答案为:C
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
14.A
【解析】要想一定是黑球,则所有球的颜色都是黑色,据此解答。
【详解】要想一定是黑球,则所有球的颜色都是黑色,因为A盒子中的球都是黑球,所以,在A盒子里一定摸到黑球。
故答案为:A
【点睛】此题主要考查根据可能性的大小涂色,总数相同的情况下,数量多的可能性大,数量少的可能性小,一个也没有的就不可能。
15.B
【分析】根据袋子里只有2个白球,从口袋中不放回,任意摸球,前两次摸2个白球,可以直接判断袋子里已经没有白球了,由此得解。
【详解】根据上面的分析可知:将2个白球和8个黑球放在一个袋子里,从口袋中不放回任意摸球,前两次摸2个白球,再摸一个球一定摸到黑球。
故答案为:B
【点睛】解答此类问题的关键是弄清题意,不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小。
16.C
【分析】在一定的条件下,一些事件的结果是可以预知的,具有确定性;一些事件的结果是不可能预知的,具有不确定性。确定的事件用“一定”“不可能”来描述,不确定的事件用“可能”来描述。
【详解】A.今天是星期一,明天是星期日,这是不可能事件,所以不能用“一定”描述,故选项错误;
B.后天刮大风,这是随机事件,可能发生,所以不能用“一定”描述,故选项错误;
C.地球每天都在转动,这是确定事件。所以能用“一定”描述,故选项正确;
D.小强比他爸爸长得高,这是随机事件,可能发生,所以不能用“一定”描述,故选项错误。
故答案为:C
【点睛】能够对确定事件和不确定事件进行区分。
17.A
【解析】四个袋子中装的都是一些黄球和蓝球,摸出黄球算获奖,A袋中6个黄球,3个蓝球,黄球的个数>蓝球的个数,摸出黄球的可能性大;B袋中黄球、篮球各4个,摸到黄球、蓝球的可能性相等;C袋中3个黄球、4个蓝球,黄球的个数<蓝球的个数,摸到蓝球的可能性大;D袋中8个黄球,10个蓝球,黄球的个数<蓝球的个数,摸到蓝球的可能性大。
【详解】A.6个黄球,3个蓝球,黄球的个数>蓝球的个数,摸出黄球的可能性大,即获奖的可能性大;
B.4个黄球,4个蓝球,黄球的个数=蓝球的个数,摸出黄球、蓝球的可能性,即获奖与不获奖可能性相等;
C.3个黄球,4个蓝球,黄球的个数<蓝球的个数,摸出黄球的可能性大小,即获奖的可能性小;
D.8个黄球,10个蓝球,黄球的个数<蓝球的个数,摸出黄球的可能性大小,即获奖的可能性小。
故答案为:A
【点睛】袋中哪种颜色球的个数多,摸到的可能性就大,反之,摸到的可能性就小。
18.B
【分析】9是3的倍数,可以从盒子里摸出一个珠子;盒子里白色珠子有7颗,黑色珠子有3颗,所以得到奖品的可能性是,得不到奖品的可能性是;据此解答。
【详解】选项A,得到奖品的可能性是,该选项不正确;
选项B,得到奖品的可能性是,得不到奖品的可能性是,<,该选项正确;
选项C,得到奖品的可能性是,得不到奖品的可能性是,<,该选项不正确;
选项D,得到奖品的可能性是,不一定得到奖品,该选项不正确;
故答案为:B
【点睛】本题考查可能性大小的实际应用,解题的关键是理解“可能”与“一定”的区别。
19.C
【分析】“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,结合实际生活,按要求进行判断即可。
【详解】A.东道主日本队可能参加;
B.所有12支队伍都可能获胜;
C.没有获得资格赛入场券的国家不可能获胜;
D.女排决赛那天可能是晴天。
故答案为:C
【点睛】此题考查的是事件的确定性和不确定性,应明确事件的确定性和不确定性,并能结合实际进行正确判断。
20.D
【分析】根据记录可知,摸到黑球的次数要大于摸到白球的次数,则再摸一次,可能摸到黑球,也可能摸到白球,摸到黑球的可能性较大。
【详解】如果再摸一次,摸到黑球的可能性大。
故答案为:D
【点睛】可能性的大小与它在总数中所占数量的多少有关。
21.B
【分析】此题主要考查了可能性的大小,因为是六位数密码只记得前五个数字,个位数字是0~9中间的任意一个,所以随便输入一个数字,错误的可能性大。
【详解】根据分析:
六位数密码只记得前五个数字,随便输入一个数字,错误的可能性大。
故答案为:B
【点睛】此题考查了对可能性的求法的运用。
22.B
【详解】略
23. 6 2的倍数
【分析】有六张不同的卡片,所以任意摸一张有1、2、3、4、5、6共6种不同的结果,2的倍数有2、4、6共3个数字,3的倍数有3、6共2个数字,所以摸到2的倍数的可能性大,据此即可解答。
【详解】根据分析可知,把分别标有数字1、2、3、4、5、6的六张卡片反扣在桌面上,任意摸一张,可能出现6种结果,摸到2的倍数的可能性大(填“2的倍数”或“3的倍数”)。
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
24. 3 黄 红
【分析】可以直接根据球的数量的多少来判断,数量多的摸到的可能性就大,数量少的摸到的可能性就小。因为盒子里黄球的个数最多,所以摸到黄球的可能性最大;盒子里红球的个数最少,所以摸到红球的可能性就最小;据此解答即可。
【详解】一个盒子里装有5个黄球,3个蓝球和2个红球,从盒子中任意摸出一个球,有3种可能的结果,摸到黄球可能性最大,摸到红球的可能性最小。
【点睛】解决此题关键是如果不需要准确地计算可能性的大小时,可以根据各种球个数的多少,直接判断可能性的大小。
25.2
【分析】两两组合,求出和小于5的一共有几组即可。
【详解】点数的和的所有可能的情况为:
1+2=3,1+3=4,1+4=5,2+3=5,2+4=6,3+4=7,
所以任抽两张,点数的和小于5有2种可能。
【点睛】列举搭配的时候按顺序搭配,可以避免重复。
26.×
【分析】判断正面朝上的可能性,要看一共有几种可能发生的情况,用1除以总数,即可得到发生的可能性。
【详解】因为硬币有两个面:一个正面、一个反面,所以,可能发生的情况只有两种,反面朝上与反面朝上的可能性都是:
所以投掷一枚硬币99次,都是正面向上,那么第100次投掷这枚硬币一定反面向上,说法错误。
故答案为:×
【点睛】投硬币事件是不确定性事件,每次投掷出现正面或反面朝上的可能性大小都是一样的,跟投掷次数无关,所以第100次可能正面朝上,可能反面朝上。
27.√
【分析】硬币只有正、反两面,抛出硬币,正面朝上的可能性是,属于不确定事件中的可能性事件,而不是一定是,由此判断即可。
【详解】根据题干分析可得:一个硬币抛1000次,正面朝上的可能性是,正面朝上可能是500次,属于不确定事件中的可能性事件,而不是一定为500次,原题说法正确。
故答案为:√
28.×
【详解】略
29.√
【分析】哪种颜色的球的数量越多,摸到的可能性就越大,所以要使任意摸一个,摸出两种颜色球的可能性相同,可得两种颜色的球的数量相等,据此求出有多少个绿球、蓝球,从而判断。
【详解】要使任意摸一个,摸出两种颜色球的可能性相同,可得两种颜色的球的数量相等,所以两种颜色的球的数量都是:
8÷2=4(个)
原题说法正确。
故答案为:√。
【点睛】解答此类问题的关键是需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答。
30.×
【分析】抛一枚5角的硬币,出现正面朝上和反面朝上的可能性是一样的,但并不是说正反面朝上的次数一定一样多,所以连续抛一枚5角的硬币20次,出现正面朝上的次数可能是10,也可能多于10,也可能少于10。
【详解】连续抛一枚5角的硬币20次,出现正面朝上的次数不一定是10,所以判断错误。
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
31.×
【分析】抛硬币时正面朝上和反面朝上的可能性是相等的,但在实际操作中,有可能两面朝上的次数各5次,也有可能出现正面朝上的次数多一些,反面朝上的次数少些。
【详解】东东抛一枚硬币,连续抛10次,有可能两面朝上的次数各5次,也可能出现一面朝上的次数多一些,而另一面朝上的次数少些。
故答案为:×
【点睛】本题考查可能性,解答本题的关键是理解抛硬币正面朝上和反面朝上的可能性是相等的。
32.√
【分析】根据摸到各种颜色的球的次数及摸球的总次数,可以推测各种球个数可能的多少,但是并不能肯定,据此判断。
【详解】32>8
红球的个数比白球可能多。说法正确;
故答案为:√
【点睛】本题主要考查可能性的大小,关键根据各种颜色的球出现的次数多少,推测其个数的多少。
33.见详解
【分析】只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等,如果没有包含该情况就不可能发生,如果包含的全部是该情况就一定能发生。
【详解】
【点睛】本题主要考查学生对可能性大小比较知识的掌握和灵活运用。
34.(1)
(2)(答案不唯一)
(3)(答案不唯一)
【分析】(1)根据游戏规则,如果希望两人打平手,红、黑两种颜色的球各放5个;
(2)根据游戏规则,如果希望洋洋赢,红球的个数应大于黑球的个数;
(3)根据游戏规则,如果希望东东赢,红球的个数应小于黑球的个数。
【详解】(1)
(2)(答案不唯一)
(3)(答案不唯一)
【点睛】不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小是解答本题的关键。
35.见详解
【分析】(1)站在超市经理的立场上考虑:一等奖的数量最少,所以放的红球数量最少;二等奖的数量比一等奖稍多,所以黄球的数量要比红球的数量稍多,三等奖的数量更多一些,所以绿球的数量比黄球再多一些;不得奖的数量最多,所以白球的数量最多。
(2)站在顾客立场上考虑:一等奖的数量最多,所以放的红球数量最多;二等奖的数量比一等奖稍少,所以黄球的数量要比红球的数量稍少,三等奖的数量更少一些,所以绿球的数量比黄球再少一些;不得奖的数量最少,所以白球的数量最少。
【详解】(1)如果我是超市经理,安排红球个数最少,黄球的数量要比红球的数量稍多,绿球的数量比黄球再多一些;白球的数量最多。
(2)如果我是顾客,放的红球数量最多;黄球的数量要比红球的数量稍少,绿球的数量比黄球再少一些;白球的数量最少。
【点睛】可能性的大小与它在总数中所占数量的多少有关。在总数中占的数量越多,摸到的可能性就越大,占的数量越少,摸到的可能性就越小。
36.可能性相同
【分析】0、6、1、8任意取三张摆成一个三位数,一共有18种不同的情况,其中末尾有0的数有:180、810、160、610、860、680,共6个。中间有0的数有:108、801、106、601、806、608,共6个。没有0的数有:618、681、168、186、861、816,共6个。据此解答即可。
【详解】从4张数字卡片 、 、 、 中任意取出3张摆成一个三位数,共18种情况。其中摆成末尾有0的数有6个,摆成中间有0的数有6个,二者可能性相同。
【点睛】可能性的大小与它在总数中所占数量的多少有关。
37.见解析
【分析】方案一:摸到三种颜色的球的可能性同样大,只要让三种颜色的球的个数相等即可;
方案二:摸到三种颜色的球各不相同,只要让三种颜色球的个数都不相同即可;
方案三:摸到红球的可能性最大,摸到黄球和蓝球的可能性相同,只要让红球最多,黄球和蓝球的个数相等即可;
方案四:摸到黄球的可能性最大,摸到红球的可能性较小,不可能摸到蓝球,只要黄球个数最多,剩下的都是红球,没有蓝球即可。
【详解】如图:
红球 黄球 蓝球
方案1 4个 4个 4个
方案2 3个 4个 5个
方案3 6个 3个 3个
方案4 1个 11个 0个
【点睛】解答此题应结合题意,根据可能性的大小把12个球按颜色进行分配即可。
答案第1页,共2页
答案第1页,共2页
