北师大版七年级数学上册 2.11有理数的混合运算一课一练(Word版含答案)
文档属性
| 名称 | 北师大版七年级数学上册 2.11有理数的混合运算一课一练(Word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-28 00:00:00 | ||
图片预览




文档简介
2.11《有理数的混合运算》
一、单选题
1.计算的结果是( )
A.-12 B.2 C.-6 D.以上都不对
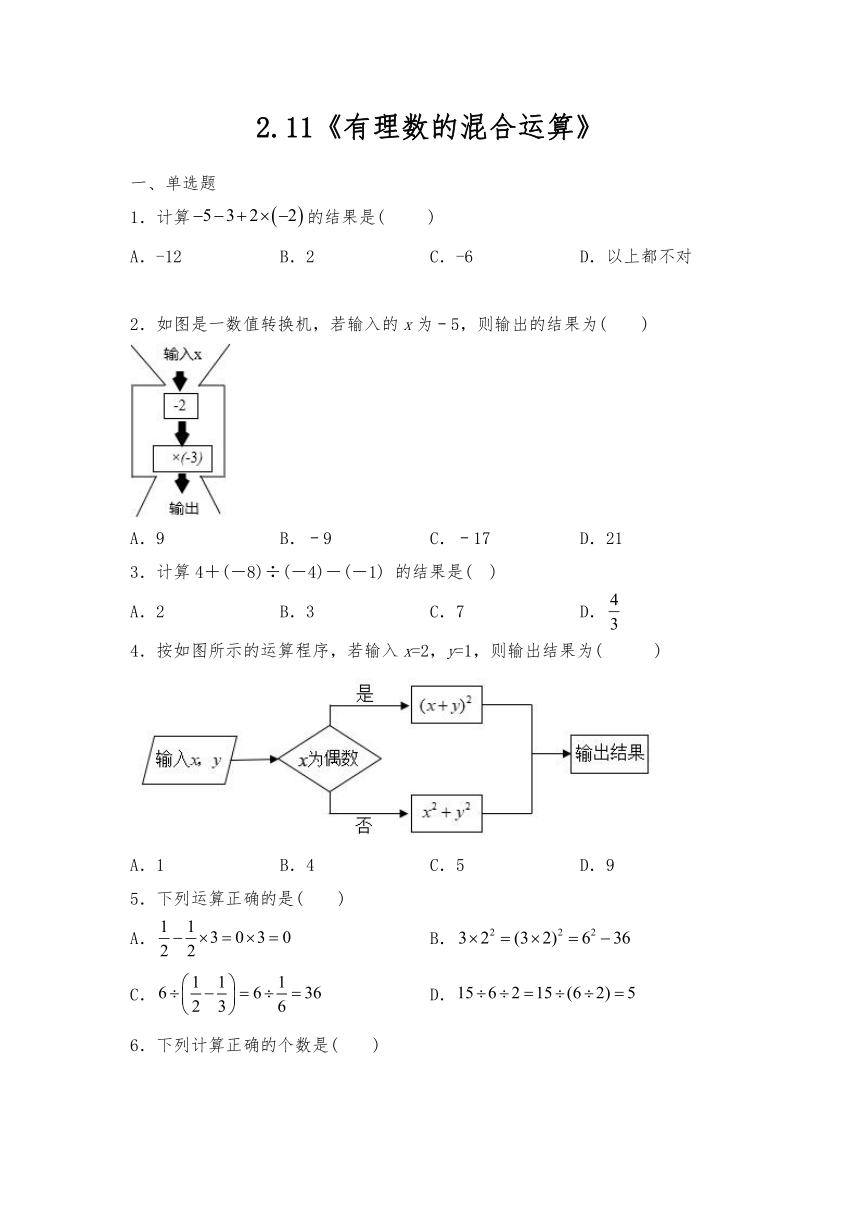
2.如图是一数值转换机,若输入的x为﹣5,则输出的结果为( )
A.9 B.﹣9 C.﹣17 D.21
3.计算4+(-8)÷(-4)-(-1) 的结果是( )
A.2 B.3 C.7 D.
4.按如图所示的运算程序,若输入x=2,y=1,则输出结果为( )
A.1 B.4 C.5 D.9
5.下列运算正确的是( )
A. B.
C. D.
6.下列计算正确的个数是( )
① ② ③ ④
⑤ ⑥ ⑦ ⑧
A.1个 B.2个 C.3个 D.以上答案均错
7.计算的结果是( )
A.-9 B.9 C. D.
8.计算:( )
A.1 B.0 C. D.
9.定义运算,如,则的值为( )
A.8 B.-8 C.16 D.-16
10.按下面的程序计算,若开始输入的值x为正整数,输出结果86,那么满足条件的x的值有( )
A.4个 B.3个 C.2个 D.1个
11.我们常用的十进制数,如我国古代《易经》一书记载,远古时期,人们通过在绳子上打结来记录数量,如图,一位母亲在从右到左依次排列的绳子上打结,并采用七进制(如)用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
A.天 B.天 C.天 D.天
12.定义☆运算:观察下列运算:
(+3)☆(+15)=+18 (-14)☆(-7)=+21
(-2)☆(+14)=-16 (+15)☆(-8)=-23
0☆(-15)=+15 (+13)☆0=+13
请你认真思考上述运算,归纳☆运算的法则,并计算:(-11)☆[0☆(–12)]等于( )
A.132 B.0 C.-132 D.-23
13.现定义运算“*”,对于任意有理数a,b满足a*b=.如5*3=2×5﹣3=7,*1=﹣2×1=﹣,若x*3=5,则有理数x的值为( )
A.4 B.11 C.4或11 D.1或11
14.2019减去它的,再减去余下的,再减去余下的,…以此类推,一直减到余下的,则最后剩下的数是( )
A.0 B.1 C. D.
15.为了求1+2+22+23+…+22019的值,可令S=1+2+22+23+…+22019,则2S=2+22+23+…+22019+22020,因此2S-S=22020-1,所以1+2+22+23+…+22019=22020-1.请仿照以上推理计算:1+4+42+43+…+42019的值是( )
A.42100-1 B.42020-1 C. D.
二、填空题
1.将四个数2,﹣3,4,﹣5进行有理数的加、减、乘、除、乘方运算,列一个算式_____(每个数都要用,且只能用一次,写出一个即可),使得运算结果等于24.
2.有三个互不相等的有理数,既可以表示为1,,a的形式,又可以表示的形式,则________.
3.用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b = ab2 + a.如:1☆3=1×32+1=10.则(-2)☆3+3☆(-2)=_____.
4.规定:符号“&”为选择两数中较大数的运算,“Δ”为选择两数中较小数的运算.则[(7Δ3)&6][5Δ(3&7)]的结果为____________.
5.你玩过24点游戏吧,请你运用加、减、乘、除运算和括号,写出数5、5、5、1得到24的算式__________(每个数只能用一次).
6.观察下列等式:
……
请按上述规律,写出第个式子的计算结果(为正整数)______.(写出最简计算结果即可)
7.阅读理解:,,……阅读以上材料后计算: =__.
8.计算:的结果是_____________.
三、解答题
1.(1)计算:.
(2).
(3)计算:.
2.小王和小李两人在进行100米跑训练,小王说:“我跑到终点时,你离终点还有20米”,小李说:“我跑到终点时,你才比我快了2.5秒”.
(1)求小王和小李的速度.
(2)若小李从起点先跑2秒后小王再开始跑,求小王起跑后几秒追上小李.
(3)若小李从起点起跑,小王在起点后20米同时起跑,小王在起跑时不慎摔了一跤,爬起来后继续按原速度跑,在跑的过程中发现某一时刻两人相距只有2米,求小王摔倒最多耽搁几秒时间?
3.学习有理数的乘法后,老师给出一道题:计算:,看看谁算得又快又对,有两位同学的解法如下:
小明:原式;
小李:原式;
(1)上面的解法对你有何启发,你认为还有简便的方法吗?若有,请写出来;
(2)用你认为最合适的方法计算:.
4.规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如,等,类比有理数的乘方,我们把记作,读作“2的3次商”,记作,读作“的4次商”.一般地,我们把n个相除记作,读作“a的n次商”.
初步探究
(1)直接写出结果:________;
(2)关于除方,下列说法错误的是_________.
①任何非零数的2次商都等于1;②对于任何正整数n,;
③;④负数的奇数次商结果是负数,负数的偶数次商结果是正数.
深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算能够转化为乘法运算,那么有理数的除方运算如何转化为乘方运算呢?
例:
(3)试一试:仿照上面的算式,将下列运算结果直接写成乘方(幂)的形式
_______;_______.
(4)想一想:将一个非零有理数a的n次商写成幂的形式等于___________;
(5)算一算:________.
答案
一、单选题
A.D.C.D.C.B.C.B.A.A.B.D.A.B.D.
二、填空题
1.2×[4﹣(﹣3)﹣(﹣5)]=24(答案不唯一).
2.0.
3.-5
4.30.
5.5×(5-1÷5)=24.
6..
7..
8..
三、解答题
1.(1)原式.
(2)原式
.
(3)原式.
2.解:(1)20÷2.5=8米/秒,
∴小李的速度为8米/秒,
100÷8=12.5秒,
100÷(12.5-2.5)=10米/秒,
∴小王的速度为:10米/秒;
(2)8×2÷(10-8)=8秒,
∴小王起跑后8秒追上小李;
(3)(20-2)÷(10-8)=9秒,
120÷10-9=3秒,
∴最多耽搁3秒.
3.解:(1)还有更简便的解法,
;
(2).
4.解:(1);
(2)当a≠0时,a2=a÷a=1,因此①正确;
对于任何正整数n,
当n为奇数时,,
当n为偶数时,,因此②错误;
因为34=3÷3÷3÷3=,而43=4÷4÷4=,因此③错误;
负数的奇数次商结果是负数,负数的偶数次商结果是正数,因此④正确;
故答案为:②③;
(3),
==;
(4)由题意可得:
将一个非零有理数a的n次商写成幂的形式等于;
(5)
=
=
=
一、单选题
1.计算的结果是( )
A.-12 B.2 C.-6 D.以上都不对
2.如图是一数值转换机,若输入的x为﹣5,则输出的结果为( )
A.9 B.﹣9 C.﹣17 D.21
3.计算4+(-8)÷(-4)-(-1) 的结果是( )
A.2 B.3 C.7 D.
4.按如图所示的运算程序,若输入x=2,y=1,则输出结果为( )
A.1 B.4 C.5 D.9
5.下列运算正确的是( )
A. B.
C. D.
6.下列计算正确的个数是( )
① ② ③ ④
⑤ ⑥ ⑦ ⑧
A.1个 B.2个 C.3个 D.以上答案均错
7.计算的结果是( )
A.-9 B.9 C. D.
8.计算:( )
A.1 B.0 C. D.
9.定义运算,如,则的值为( )
A.8 B.-8 C.16 D.-16
10.按下面的程序计算,若开始输入的值x为正整数,输出结果86,那么满足条件的x的值有( )
A.4个 B.3个 C.2个 D.1个
11.我们常用的十进制数,如我国古代《易经》一书记载,远古时期,人们通过在绳子上打结来记录数量,如图,一位母亲在从右到左依次排列的绳子上打结,并采用七进制(如)用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
A.天 B.天 C.天 D.天
12.定义☆运算:观察下列运算:
(+3)☆(+15)=+18 (-14)☆(-7)=+21
(-2)☆(+14)=-16 (+15)☆(-8)=-23
0☆(-15)=+15 (+13)☆0=+13
请你认真思考上述运算,归纳☆运算的法则,并计算:(-11)☆[0☆(–12)]等于( )
A.132 B.0 C.-132 D.-23
13.现定义运算“*”,对于任意有理数a,b满足a*b=.如5*3=2×5﹣3=7,*1=﹣2×1=﹣,若x*3=5,则有理数x的值为( )
A.4 B.11 C.4或11 D.1或11
14.2019减去它的,再减去余下的,再减去余下的,…以此类推,一直减到余下的,则最后剩下的数是( )
A.0 B.1 C. D.
15.为了求1+2+22+23+…+22019的值,可令S=1+2+22+23+…+22019,则2S=2+22+23+…+22019+22020,因此2S-S=22020-1,所以1+2+22+23+…+22019=22020-1.请仿照以上推理计算:1+4+42+43+…+42019的值是( )
A.42100-1 B.42020-1 C. D.
二、填空题
1.将四个数2,﹣3,4,﹣5进行有理数的加、减、乘、除、乘方运算,列一个算式_____(每个数都要用,且只能用一次,写出一个即可),使得运算结果等于24.
2.有三个互不相等的有理数,既可以表示为1,,a的形式,又可以表示的形式,则________.
3.用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b = ab2 + a.如:1☆3=1×32+1=10.则(-2)☆3+3☆(-2)=_____.
4.规定:符号“&”为选择两数中较大数的运算,“Δ”为选择两数中较小数的运算.则[(7Δ3)&6][5Δ(3&7)]的结果为____________.
5.你玩过24点游戏吧,请你运用加、减、乘、除运算和括号,写出数5、5、5、1得到24的算式__________(每个数只能用一次).
6.观察下列等式:
……
请按上述规律,写出第个式子的计算结果(为正整数)______.(写出最简计算结果即可)
7.阅读理解:,,……阅读以上材料后计算: =__.
8.计算:的结果是_____________.
三、解答题
1.(1)计算:.
(2).
(3)计算:.
2.小王和小李两人在进行100米跑训练,小王说:“我跑到终点时,你离终点还有20米”,小李说:“我跑到终点时,你才比我快了2.5秒”.
(1)求小王和小李的速度.
(2)若小李从起点先跑2秒后小王再开始跑,求小王起跑后几秒追上小李.
(3)若小李从起点起跑,小王在起点后20米同时起跑,小王在起跑时不慎摔了一跤,爬起来后继续按原速度跑,在跑的过程中发现某一时刻两人相距只有2米,求小王摔倒最多耽搁几秒时间?
3.学习有理数的乘法后,老师给出一道题:计算:,看看谁算得又快又对,有两位同学的解法如下:
小明:原式;
小李:原式;
(1)上面的解法对你有何启发,你认为还有简便的方法吗?若有,请写出来;
(2)用你认为最合适的方法计算:.
4.规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如,等,类比有理数的乘方,我们把记作,读作“2的3次商”,记作,读作“的4次商”.一般地,我们把n个相除记作,读作“a的n次商”.
初步探究
(1)直接写出结果:________;
(2)关于除方,下列说法错误的是_________.
①任何非零数的2次商都等于1;②对于任何正整数n,;
③;④负数的奇数次商结果是负数,负数的偶数次商结果是正数.
深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算能够转化为乘法运算,那么有理数的除方运算如何转化为乘方运算呢?
例:
(3)试一试:仿照上面的算式,将下列运算结果直接写成乘方(幂)的形式
_______;_______.
(4)想一想:将一个非零有理数a的n次商写成幂的形式等于___________;
(5)算一算:________.
答案
一、单选题
A.D.C.D.C.B.C.B.A.A.B.D.A.B.D.
二、填空题
1.2×[4﹣(﹣3)﹣(﹣5)]=24(答案不唯一).
2.0.
3.-5
4.30.
5.5×(5-1÷5)=24.
6..
7..
8..
三、解答题
1.(1)原式.
(2)原式
.
(3)原式.
2.解:(1)20÷2.5=8米/秒,
∴小李的速度为8米/秒,
100÷8=12.5秒,
100÷(12.5-2.5)=10米/秒,
∴小王的速度为:10米/秒;
(2)8×2÷(10-8)=8秒,
∴小王起跑后8秒追上小李;
(3)(20-2)÷(10-8)=9秒,
120÷10-9=3秒,
∴最多耽搁3秒.
3.解:(1)还有更简便的解法,
;
(2).
4.解:(1);
(2)当a≠0时,a2=a÷a=1,因此①正确;
对于任何正整数n,
当n为奇数时,,
当n为偶数时,,因此②错误;
因为34=3÷3÷3÷3=,而43=4÷4÷4=,因此③错误;
负数的奇数次商结果是负数,负数的偶数次商结果是正数,因此④正确;
故答案为:②③;
(3),
==;
(4)由题意可得:
将一个非零有理数a的n次商写成幂的形式等于;
(5)
=
=
=
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
