人教版九年级上册24.2.2 直线和圆的位置关系 课件(共19张PPT)
文档属性
| 名称 | 人教版九年级上册24.2.2 直线和圆的位置关系 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-28 07:54:27 | ||
图片预览




文档简介
(共19张PPT)
24.2.2 直线和圆的位置关系(1)
第二十四章 圆
探究新知
-----海平面
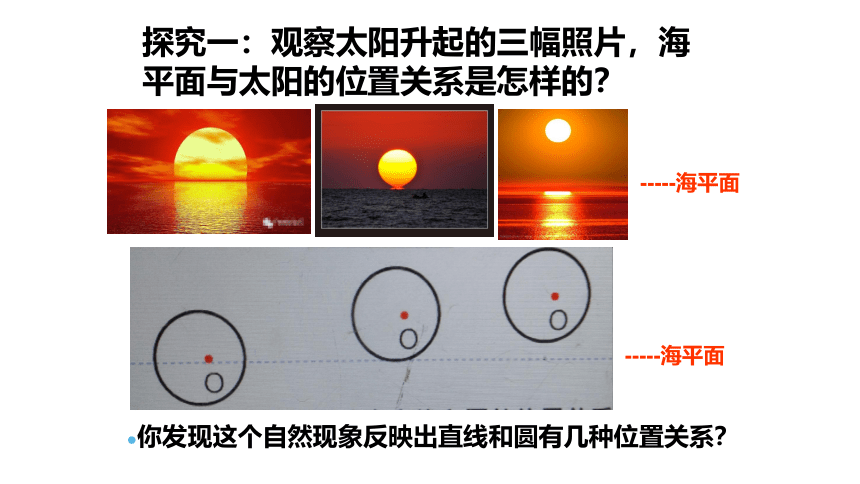
探究一:观察太阳升起的三幅照片,海平面与太阳的位置关系是怎样的?
-----海平面
●你发现这个自然现象反映出直线和圆有几种位置关系?
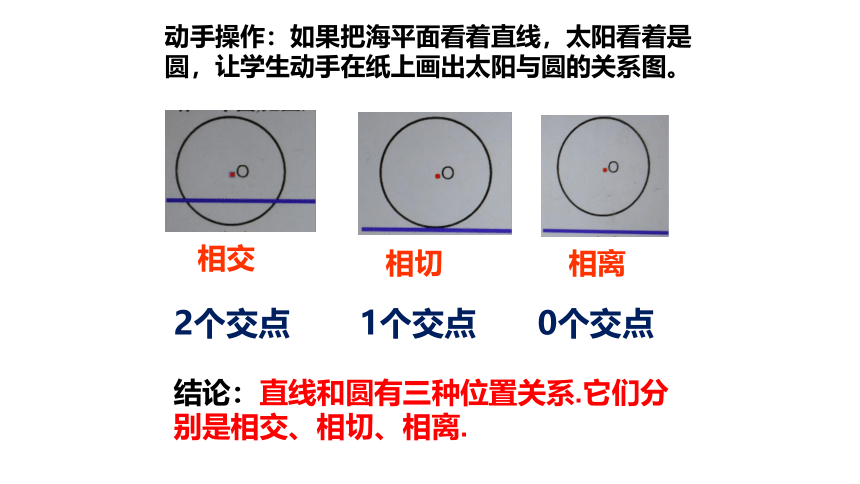
相交
相切
相离
结论:直线和圆有三种位置关系.它们分别是相交、相切、相离.
动手操作:如果把海平面看着直线,太阳看着是圆,让学生动手在纸上画出太阳与圆的关系图。
2个交点
1个交点
0个交点
直线与圆有两个公共点时,叫做直线和圆相交,这条直线叫圆的割线.
直线和圆有唯一公共点时,这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点。
当直线与圆没有公共点时,叫做直线和圆相离.
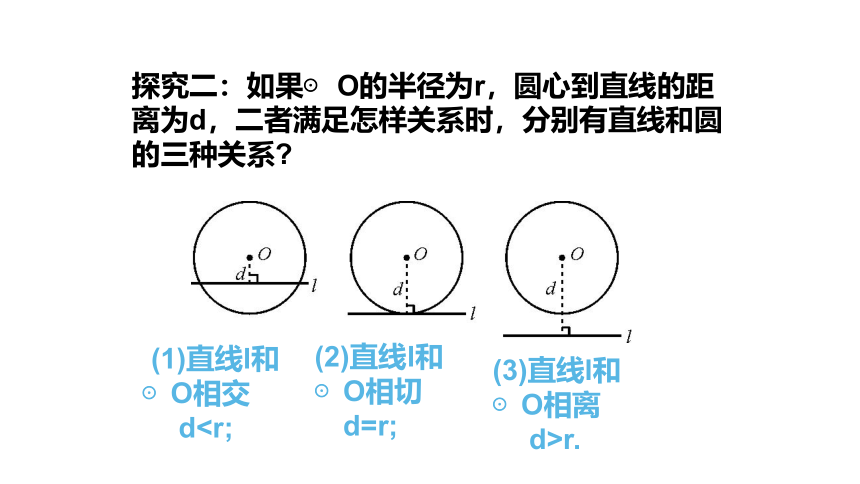
探究二:如果⊙ O的半径为r,圆心到直线的距离为d,二者满足怎样关系时,分别有直线和圆的三种关系
(1)直线l和 ⊙O相交
? d(2)直线l和⊙O相切?d=r;
(3)直线l和⊙O相离
? d>r.
1、圆的直径是13cm,如果直线与圆心的距离d分别如下,判断直线与圆的位置关系,并说明有几个公共点.
(1)4.5cm (2)6.5cm (3)8cm
答:(1)直线与圆的位置关系是相交,有2个公共点;
(2)直线与圆的位置关系是相切,有1个公共点;
(3)直线与圆的位置关系是相离,没有公共点。
练习
半径为6.5CM
直线和圆位置关系的特点
直线与圆的位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2
1
0
交点
切点
无
割线
切线
无
d<r
d =r
d >r
归纳
24.2.2直线和圆的位置关系(2)目录CONTENTS
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与⊙O1相离
直线l与 ⊙O2相交
O
(从直线与圆公共点的个数)
●
●
●
●
●
判一判
导入
一个小岛的周围有环岛暗礁,暗礁分布以小岛的中心为圆心,半径为47km的圆形区域。已知小岛中心位于轮船正西80km处,港口位于小岛中心正北60km处,如果轮船沿直线返航,那么它是否会有触礁危险?
探一探
导入
点到圆心的距离d与半径r的关系判断
点C在圆外 d>r;
点B在圆上 d=r;
点A在圆内 dA
B
C
引一引
知识讲解
直线与圆的位置关系(数量特征----用圆心到直线的距离d与半径r来区分)
我们一起再来归纳
知识讲解
d
r
相切
.A
.
C
.O
r
d
相交
.
C
. A
O
1、直线与圆相交
2、直线与圆相切
3、直线与圆相离
dd=r
d>r
d
r
相离
.A
.
C
.O
知识讲解
一个小岛的周围有环岛暗礁,暗礁分布以小岛的中心为圆心,半径为47km的圆形区域。已知小岛中心位于轮船正西80km处,港口位于小岛中心正北60km处,如果轮船沿直线返航,那么它是否会有触礁危险?
以小岛的中心为圆心,东西方向为轴,南北方向为轴建立直角坐标系,则问题归结为圆心到直线的距离与半径关系的问题
讲一讲
知识讲解
课堂练习如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.【详解】解:如图,连接OA,作直径MN⊥AB,垂足为D,由垂径定理可知:AD=DB= AB=4(cm),∵圆的直径为10cm,∴DA=5cm,由勾股定理得:OD=3(cm),∵垂线段最短,半径最大,∴OP长度范围为:3≤OP≤5(cm)【课堂小结】
小结
通过学习,我们会灵活准确运用圆心到
直线的距离d与半径r来解决实际问题。
谢谢聆听
24.2.2 直线和圆的位置关系(1)
第二十四章 圆
探究新知
-----海平面
探究一:观察太阳升起的三幅照片,海平面与太阳的位置关系是怎样的?
-----海平面
●你发现这个自然现象反映出直线和圆有几种位置关系?
相交
相切
相离
结论:直线和圆有三种位置关系.它们分别是相交、相切、相离.
动手操作:如果把海平面看着直线,太阳看着是圆,让学生动手在纸上画出太阳与圆的关系图。
2个交点
1个交点
0个交点
直线与圆有两个公共点时,叫做直线和圆相交,这条直线叫圆的割线.
直线和圆有唯一公共点时,这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点。
当直线与圆没有公共点时,叫做直线和圆相离.
探究二:如果⊙ O的半径为r,圆心到直线的距离为d,二者满足怎样关系时,分别有直线和圆的三种关系
(1)直线l和 ⊙O相交
? d
(3)直线l和⊙O相离
? d>r.
1、圆的直径是13cm,如果直线与圆心的距离d分别如下,判断直线与圆的位置关系,并说明有几个公共点.
(1)4.5cm (2)6.5cm (3)8cm
答:(1)直线与圆的位置关系是相交,有2个公共点;
(2)直线与圆的位置关系是相切,有1个公共点;
(3)直线与圆的位置关系是相离,没有公共点。
练习
半径为6.5CM
直线和圆位置关系的特点
直线与圆的位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2
1
0
交点
切点
无
割线
切线
无
d<r
d =r
d >r
归纳
24.2.2直线和圆的位置关系(2)目录CONTENTS
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与⊙O1相离
直线l与 ⊙O2相交
O
(从直线与圆公共点的个数)
●
●
●
●
●
判一判
导入
一个小岛的周围有环岛暗礁,暗礁分布以小岛的中心为圆心,半径为47km的圆形区域。已知小岛中心位于轮船正西80km处,港口位于小岛中心正北60km处,如果轮船沿直线返航,那么它是否会有触礁危险?
探一探
导入
点到圆心的距离d与半径r的关系判断
点C在圆外 d>r;
点B在圆上 d=r;
点A在圆内 d
B
C
引一引
知识讲解
直线与圆的位置关系(数量特征----用圆心到直线的距离d与半径r来区分)
我们一起再来归纳
知识讲解
d
r
相切
.A
.
C
.O
r
d
相交
.
C
. A
O
1、直线与圆相交
2、直线与圆相切
3、直线与圆相离
d
d>r
d
r
相离
.A
.
C
.O
知识讲解
一个小岛的周围有环岛暗礁,暗礁分布以小岛的中心为圆心,半径为47km的圆形区域。已知小岛中心位于轮船正西80km处,港口位于小岛中心正北60km处,如果轮船沿直线返航,那么它是否会有触礁危险?
以小岛的中心为圆心,东西方向为轴,南北方向为轴建立直角坐标系,则问题归结为圆心到直线的距离与半径关系的问题
讲一讲
知识讲解
课堂练习如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.【详解】解:如图,连接OA,作直径MN⊥AB,垂足为D,由垂径定理可知:AD=DB= AB=4(cm),∵圆的直径为10cm,∴DA=5cm,由勾股定理得:OD=3(cm),∵垂线段最短,半径最大,∴OP长度范围为:3≤OP≤5(cm)【课堂小结】
小结
通过学习,我们会灵活准确运用圆心到
直线的距离d与半径r来解决实际问题。
谢谢聆听
同课章节目录
