【最新强化训练】冀教版九下 第三十章二次函数单元测试练习题(含解析)
文档属性
| 名称 | 【最新强化训练】冀教版九下 第三十章二次函数单元测试练习题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 16:24:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学下册第三十章二次函数单元测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题 ( http: / / www.21cnjy.com )目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21*cnjy*com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x … -3 -2 -1 0 1 …
y … -6 0 4 6 6 …
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的右侧;
③抛物线的开口向下;
④抛物线与x轴有且只有1个公共点.
以上说法正确是( )
A.① B.①② C.①②③ D.①②③④
2、将关于x的二次函数的图像向上平移1单位,得到的抛物线经过三点、、,则、、的大小关系是( )2-1-c-n-j-y
A. B. C. D.
3、下列实际问题中的y与x之间的函数表达式是二次函数的是( )
A.正方体集装箱的体积,棱长xm
B.小莉驾车以的速度从南京出发到上海,行驶xh,距上海ykm
C.妈妈买烤鸭花费86元,烤鸭的重量y斤,单价为x元/斤
D.高为14m的圆柱形储油罐的体积,底面圆半径xm
4、抛物线,,的图象开口最大的是( )
A. B. C. D.无法确定
5、抛物线y=﹣2(x﹣3)2﹣4的对称轴是( )
A.直线x=3 B.直线x=﹣3 C.直线x=4 D.直线x=﹣4
6、如图,抛物线与轴交于点,对称轴为直线,则下列结论中正确的是( )
( http: / / www.21cnjy.com / )
A.
B.当时,随的增大而增大
C.
D.是一元二次方程的一个根
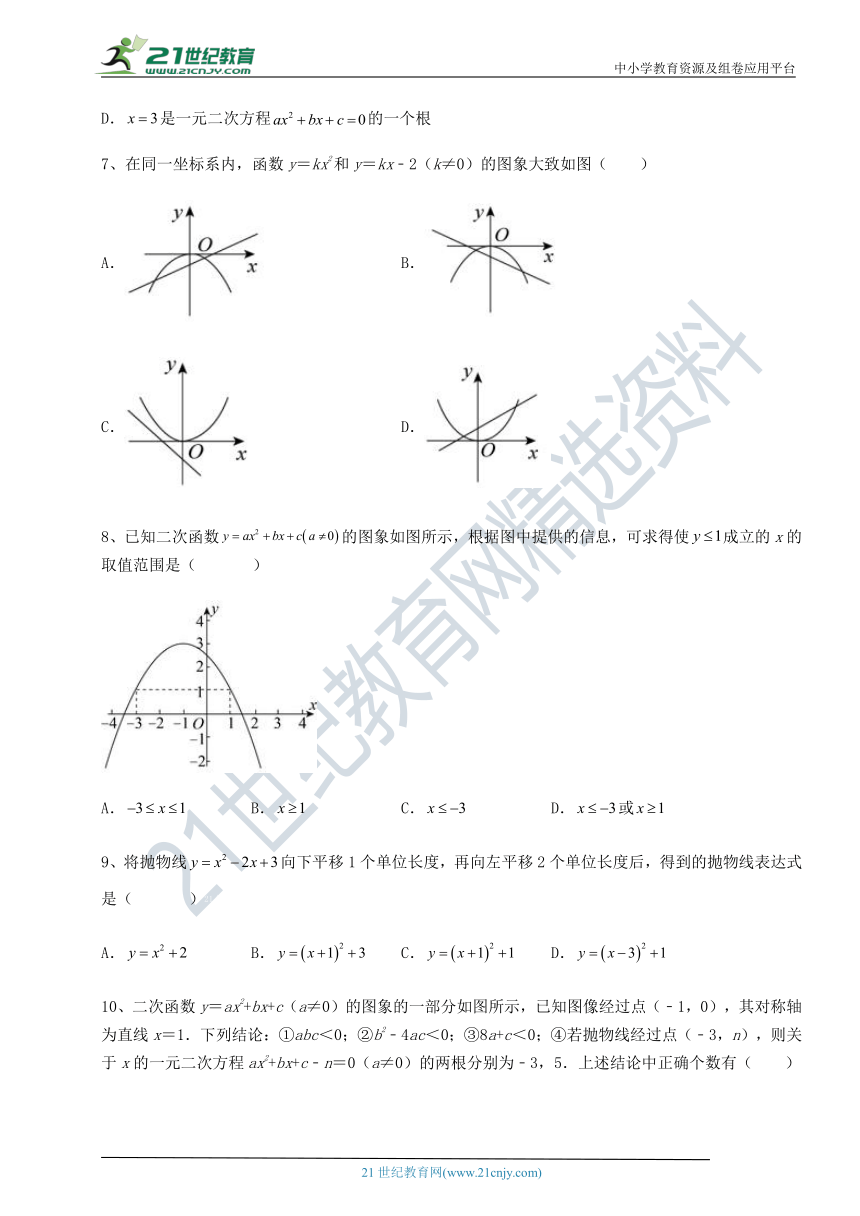
7、在同一坐标系内,函数y=kx2和y=kx﹣2(k≠0)的图象大致如图( )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )
C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
8、已知二次函数的图象如图所示,根据图中提供的信息,可求得使成立的x的取值范围是( )21*cnjy*com
( http: / / www.21cnjy.com / )
A. B. C. D.或
9、将抛物线向下平移1个单位长度,再向左平移2个单位长度后,得到的抛物线表达式是( )21教育名师原创作品
A. B. C. D.
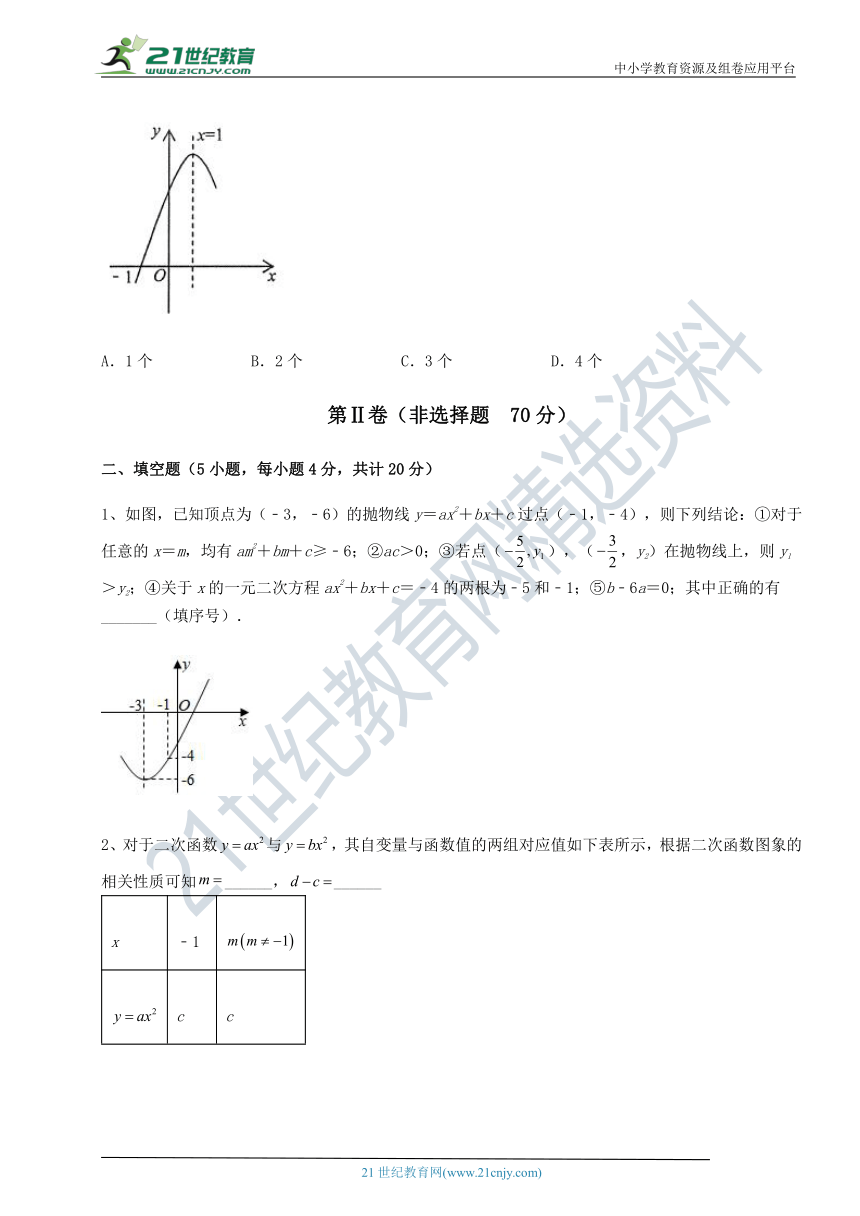
10、二次函数y=ax2+bx ( http: / / www.21cnjy.com )+c(a≠0)的图象的一部分如图所示,已知图像经过点(﹣1,0),其对称轴为直线x=1.下列结论:①abc<0;②b2﹣4ac<0;③8a+c<0;④若抛物线经过点(﹣3,n),则关于x的一元二次方程ax2+bx+c﹣n=0(a≠0)的两根分别为﹣3,5.上述结论中正确个数有( )
( http: / / www.21cnjy.com / )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c过点(﹣1,﹣4),则下列结论:①对于任意的x=m,均有am2+bm+c≥﹣6;②ac>0;③若点(),(,y2)在抛物线上,则y1>y2;④关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1;⑤b﹣6a=0;其中正确的有_______(填序号).【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
2、对于二次函数与,其自变量与函数值的两组对应值如下表所示,根据二次函数图象的相关性质可知______,______
x ﹣1
c c
d
3、抛物线的顶点坐标是______.
4、已知抛物线经过点.若点在该抛物线上,且,则n的取值范围为______.
5、二次函数y=ax2+bx+c的部分对应值列表如下:
x … ﹣3 0 1 3 5 …
y … 7 ﹣8 ﹣9 ﹣5 7 …
则一元二次方程a(2x+1)2+b(2x+1)+c=﹣5的解为 _____.
三、解答题(5小题,每小题10分,共计50分)
1、图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m.以O为原点,OA所在直线为x轴建立直角坐标系,若点P的坐标为.
( http: / / www.21cnjy.com / )
(1)求拱桥所在抛物线的函数表达式;
(2)因降暴雨水位上升1m,此时水面宽为多少?(结果保留根号)
2、在平面直角坐标系中,二次函 ( http: / / www.21cnjy.com )数y=﹣x2+bx+c的图象经过点(2,3),且交x轴于A(﹣1,0)、B(m,0),求m的值及二次函数图象的对称轴.
3、已知一抛物线的顶点为(2,4),图象过点(1,3).
(1)求抛物线的解析式;
(2)动点P(x,5)能否在抛物线上?请说明理由;
(3)若点A(a,y1),B(b,y2)都在抛物线上,且a<b<0,比较y1,y2的大小,并说明理由.
4、阅读理解,并完成相应的问题.
如图,重庆轨道2号线是中国 ( http: / / www.21cnjy.com )西部地区第一条城市轨道交通线路,也是中国第一条跨座式单轨线路,因其列车在李子坝站穿楼而过闻名全国.小军了解到列车从牛角沱站开往李子坝站时,在距离停车线256米处开始减速.他想知道列车从减速开始,经过多少秒停下来,以及最后一秒滑行的距离.为了解决这个问题,小军通过建立函数模型来描述列车离停车线的距离s(米)与滑行时间t(秒)的函数关系,再应用该函数解决相应的问题.
( http: / / www.21cnjy.com / )
(1)建立模型
①收集数据:
r(秒) 0 4 8 12 16 20 24 ……
s(米) 256 196 144 100 64 36 16 ……
②建立平面直角坐标系为了观察s(米)与t(秒)的关系,建立如图所示的平面直角坐标系.
③描点连线:请在平面直角坐标系中将表中未描出的点补充完整,并用平滑的曲线依次连接.
④选择函数模型:观察这条曲线的形状,它可能是_______函数的图象.
⑤求函数解析式;
解:设,因为时,,所以,则.
请根据表格中的数据,求a,b的值.(请写出详细解答过程).
( http: / / www.21cnjy.com / )
验证:把a,b的值代入中,并将其余几对值代入求出的解析式,发现它们_______满足该函数解析式.(填“都”或“不都”)21教育网
结论:减速阶段列车离停车线的距离s(米)与减速时间t(秒)的函数关系式为__________.
(2)应用模型
列车从减速开始经过_______秒,列车停止;最后一秒钟,列车滑行的距离为_______米.
5、如图1,已知抛物线交x轴于A,B两点,交y轴于点C,点P是直线上一动点.
( http: / / www.21cnjy.com / )
(1)求直线的解析式;
(2)若点P关于原点O的对称点Q刚好落在抛物线上,求点P的坐标;
(3)如图2,连接,过点P作PEBC交x轴于点E,连接,将沿对折,点P的对应点恰好落在x轴上时,求点E的坐标.【版权所有:21教育】
-参考答案-
一、单选题
1、C
【解析】
【分析】
根据表中数据和抛物线的对称性,可得抛物线的对称轴是直线x=,可得到抛物线的开口向下,再根据抛物线的性质即可进行判断.
【详解】
解:根据图表,抛物线与y轴交于(0,6),故①正确;
∵抛物线经过点(0,6)和(1,6),
∴对称轴为x==>0,即抛物线的对称轴在y轴的右侧,故②正确;
当x<时,y随x的增大而增大,
∴抛物线开口向下,故③正确,
∵抛物线经过点(-2,0),
设抛物线经过点(x,0),
∴x==,
解得:x=3,
∴抛物线经过(3,0),即抛物线与x轴有2个交点(-2,0)和(3,0),
故④错误;
综上,正确的有①②③,
故选:C.
【点睛】
本题考查了二次函数及其图象性质,解决问题的关键是注意表格数据的特点,结合二次函数性质作判断.
2、C
【解析】
【分析】
根据题意求得平移后的二次函数的对称轴以及开口方向,根据三个点与对称轴的距离大小判断函数值的大小即可
【详解】
解:∵关于x的二次函数的图像向上平移1单位,得到的抛物线解析式为,
∴新抛物线的对称轴为,开口方向向上,则当抛物线上的点距离对称轴越远,其纵坐标越大,即函数值越大,
平移后的抛物线经过三点、、,
故选C
【点睛】
本题考查了二次函数的平移,二次函数的性质,二次函数的对称轴直线x=,图象具有如下性质:①当a>0时,抛物线的开口向上,x<时,y随x的增大而减小;x>时,y随x的增大而增大;x=时,y取得最小值,即顶点是抛物线的最低点.②当a<0时,抛物线的开口向下,x<时,y随x的增大而增大;x>时,y随x的增大而减小;x=时,y取得最大值,即顶点是抛物线的最高点,掌握二次函数的性质是解题的关键.21·世纪*教育网
3、D
【解析】
【分析】
根据题意,列出关系式,即可判断是否是二次函数.
【详解】
A.由题得:,不是二次函数,故此选项不符合题意;
B.由题得:,不是二次函数,故此选项不符合题意;
C.由题得:,不是二次函数,故此选项不符合题意;
D.由题得:,是二次函数,故此选项符合题意.
故选:D.
【点睛】
本题考查二次函数的定义,形如的形式为二次函数,掌握二次函数的定义是解题的关键.
4、A
【解析】
【分析】
先令x=1,求出函数值,然后再比较二次项系数的绝对值的大小即可解答.
【详解】
解:当x=1时,三条抛物线的对应点是(1,)(1,-3),(1,1),
∵||<|1|<|-3|,
∴抛物线开口最大.
故选A.
【点睛】
本题主要考查了二次函数图象的性质,掌握二次函数解析式的二次项系数的绝对值越小,函数图象的开口越大.
5、A
【解析】
【分析】
直接利用抛物线y=﹣2(x﹣3)2﹣4,求得对称轴方程为:x=3.
【详解】
解:抛物线y=﹣2(x﹣3)2﹣4的对称轴方程为:直线x=3,
故选:A.
【点睛】
本题考查了二次函数的性质与图象,解题的关键是掌握:二次函数的顶点式与对称轴的关系.
6、D
【解析】
【分析】
根据二次函数图象的开口方向向下可得是负数,对称轴位于轴的右侧可得、异号;与轴的交点在正半轴可得是正数,根据二次函数的增减性可得选项错误,根据抛物线的对称轴结合与轴的一个交点的坐标可以求出与轴的另一交点坐标,也就是一元二次方程的根,从而得解.
【详解】
解:、根据图象,二次函数开口方向向下,则,对称轴位于轴的右侧可得、异号,即,故本选项结论错误;21世纪教育网版权所有
B、当时,随的增大而减小,故本选项结论错误;
C、根据图象,抛物线与轴的交点在正半轴,则,故本选项结论错误;
D、抛物线与轴的一个交点坐标是,对称轴是直线,
设另一交点为,
,
,
另一交点坐标是,
是一元二次方程的一个根,
故本选项结论正确.
故选:D.
【点睛】
本题主要考查了二次函数图象与系数的关系,二次函数图象的增减性,抛物线与轴的交点问题,熟记二次函数的性质以及函数图象与系数的关系是解题的关键.2·1·c·n·j·y
7、B
【解析】
【分析】
分别利用函数解析式分析图象得出答案.
【详解】
解:A、二次函数开口向下,k<0;一次函数图象经过第一、三象限,k>0,故此选项错误;
B、两函数图象符合题意;
C、二次函数开口向上,k>0;一次函数图象经过第二、四象限,k<0,故此选项错误;
D、一次函数解析式为:y=kx-2,图象应该与y轴交在负半轴上,故此选项错误.
故选:B.
【点睛】
此题主要考查了二次函数的图象以及一次函数的图象,正确得出k的符号是解题关键.
8、D
【解析】
【分析】
根据函数图象写出y=1对应的自变量x的值,再根据判断范围即可.
【详解】
由图可知,使得时
使成立的x的取值范围是或
故选:D.
【点睛】
本题考查了二次函数与不等式,准确识图是解题的关键.
9、C
【解析】
【分析】
根据平移的规律:左加右减,上加下减可得函数解析式.
【详解】
解:因为y=x2-2x+3=(x-1)2+2.
所以将抛物线y=(x-1)2+2先向下 ( http: / / www.21cnjy.com )平移1个单位长度,再向左平移2个单位长度后,得到的抛物线的表达式为y=(x-1+2)2+2-1,即y=(x+1)2+1.21cnjy.com
故选:C.
【点睛】
本题主要考查了二次函数图象与几何变换,关键是掌握平移的规律.
10、C
【解析】
【分析】
根据图象可判断abc的符号,可判断结论①, ( http: / / www.21cnjy.com )由图象与x轴的交点个数可判断②,由对称轴及x= 2时的函数值即可判断③,由x= 3和对称轴即可判断④.【来源:21cnj*y.co*m】
【详解】
解:∵图象开口向下,
∴a<0,
∵对称轴为直线x=1,
∴ =1,
∴b= 2a>0,
∵图象与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,
∴①说法正确,
由图象可知抛物线与x轴有两个交点,
∴b2 4ac>0,
∴②错误,
由图象可知,当x= 2时,y<0,
∴4a 2b+c=4a 2( 2a)+c=8a+c<0,
∴③正确,
由题意可知x= 3是ax2+bx+c n=0(a≠0)的一个根,
∵对称轴是x=1,
∴另一个根为x=5,
∴④正确,
∴正确的有①③④,
故选:C.
【点睛】
本题主要考查二次函数的图象与性质,关键是要牢记图象与各系数之间的关系.
二、填空题
1、①④⑤
【解析】
【分析】
根据二次函数的开口方向、对称轴、顶点坐标、增减性以及二次函数与一元二次方程的关系综合进行判断即可.
【详解】
解:∵抛物线y=ax2+bx+c的顶点为(﹣3,﹣6),
∴当x=﹣3时,y最小值=﹣6,
∴对于任意的x=m,其函数值y=am2+bm+c≥﹣6,
因此①正确;
∵开口向上,
∴a>0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴ac<0,
因此②不正确;
∵点(),(,y2)在对称轴右侧的抛物线上,根据在对称轴右侧,y随x的增大而增大,
∴y1<y2,
因此③不正确;
∵抛物线y=ax2+bx+c过点(﹣1,﹣4),由对称轴为x=﹣3,根据对称性可知,抛物线y=ax2+bx+c还过点(﹣5,﹣4),21·cn·jy·com
∴当y=﹣4时,即方程ax2+bx+c=﹣4有两个不相等的实数根﹣1和﹣5,
因此④正确;
∵对称轴x=﹣=﹣3,
∴b﹣6a=0,
因此⑤正确;
综上所述,正确的结论有①④⑤,
【点睛】
本题考查了二次函数的开口方向、对称轴、顶点坐标、增减性以及二次函数与一元二次方程的关系综合,掌握二次函数的图象与性质是解题的关键.【出处:21教育名师】
2、 1 3
【解析】
【分析】
根据二次函数的性质可知m=1,将d用含c的式子表示出来即可.
【详解】
解由二次函数的性质可得的对称轴为y轴,故由表可得,
∴m=1;
∵二次函数的对称轴为y轴,
∴d=c+3,
∴3,
故答案为:1,3.
【点睛】
此题考查二次函数的对称性,熟练掌握二次函数的性质是解题的关键.
3、 (2,-1)
【解析】
【分析】
先把抛物线配方为顶点式,再确定顶点坐标即可.
【详解】
解:,
∴抛物线的顶点坐标为(2,-1).
故答案为(2,-1).
【点睛】
本题考查抛物线的顶点坐标,掌握抛物线配方为顶点式的方法是解题关键.
4、
【解析】
【分析】
将点代入求出抛物线的解析式,再求出对称轴为直线,开口向上,自变量离对称轴越远,因变量越大即可求解.www.21-cn-jy.com
【详解】
解:将代入中得到:,
解得,
∴抛物线的对称轴为直线,且开口向上,
根据“自变量离对称轴越远,其对应的因变量越大”可知,
当时,对应的最大为:,
当时,对应的最小为:,
故n的取值范围为:,
故答案为:.
【点睛】
本题考查二次函数的图像及性质,点在抛物线上,将点的坐标代入即可求解.
5、,
【解析】
【分析】
从表中找到三对数值,将三对数值分别代入y=ax2+bx+c组成方程组,求出a、b、c的值,然后再运用因式分解法求解方程即可得到结论.
【详解】
解:将(-3,7),(0,-8),(1,-9)代入y=ax2+bx+c得,
整理得,
②×3+①,得
∴
把代入②得,
∴
又
∴一元二次方程a(2x+1)2+b(2x+1)+c=﹣5可变形为:
即:
∴
∴,或
解得,,
故答案为:,
【点睛】
本题考查了待定系数法求函数解析式和一元二次方程的解法,从图表中找到相关的量是解题的关键.
三、解答题
1、 (1)
(2)
【解析】
【分析】
(1)利用待定系数法求解可得;
(2)在所求函数解析式中求出时的值即可得.
(1)
解:设抛物线的解析式为,
将点、代入,得:,
解得:,
所以抛物线的解析式为;
(2)
当时,,即,
解得:,
则水面的宽为.
【点睛】
本题主要考查二次函数的应用,解题的关键是将实际问题转化为二次函数的问题求解,并熟练掌握待定系数法求函数解析式.
2、m=3,对称轴为直线x=1
【解析】
【分析】
先根据待定系数法求出二次函数的解析式,令y=0求解x即可求得m,进而可求得二次函数图象的对称轴.
【详解】
解:将(2,3)和(-1,0)代入y=﹣x2+bx+c中,
得:,解得:,
∴y=﹣x2+2x+3,
令y=0,则﹣x2+2x+3=0,即x2﹣2x﹣3=0,
解得:x1=-1,x2=3,
∴该二次函数图象与x轴的交点坐标为A(-1,0)和B(3,0),
∴m=3,
该二次函数图象的对称轴为直线x=1.
【点睛】
本题考查待定系数法求二次 ( http: / / www.21cnjy.com )函数解析式、二次函数图象与坐标轴的交点问题、二次函数图象的对称轴,熟练掌握待定系数法求函数解析式的步骤是解答的关键.
3、 (1)
(2)不在,见解析
(3)y1<y2,见解析
【解析】
【分析】
(1)根据已知条件设抛物线的解析式为顶点式,把点(1,3)的坐标代入所设的解析式中即可求得a,从而可求得函数解析式;
(2)把点P的纵坐标代入抛物线的解析式中,得到关于x的二元一次方程,若方程有解,则点P在抛物线,否则不在抛物线上;
(3)抛物线的对称轴为直线x=2,根据抛物线的增减性质即可比较大小.
(1)
设抛物线的解析式为
把点(1,3)的坐标代入中,得a+4=3
∴
即抛物线的解析式为;
(2)
动点P(x,5)不在抛物线上
理由如下:
在中,当y=5时,得
即
此方程无解
故点P不在抛物线上;
(3)
y1<y2
理由如下:
抛物线的对称轴为直线x=2
∵二次项系数 1<0,且
∴函数值随自变量的增大而增大
即y1<y2
【点睛】
本题考查了待定系数法求二次函 ( http: / / www.21cnjy.com )数的解析式,二次函数与一元二次方程的关系,二次函数的图象与性质等知识,熟练掌握这些知识是关键,属于二次函数的基础题目.
4、 (1)二次, 都, s=
(2)32,0.25
【解析】
【分析】
(1)通过描点、连线,观察图形 ( http: / / www.21cnjy.com )可知,图象可能是二次函数的函数的图象;将点(4,196),(8,144)代入s=at2+bt+256,得a、b的值,再将其余几对值代入求出的解析式,发现它们都满足该函数解析式,最后得到结论:减速阶段列车离停车线的距离s(米)与减速时间t(秒)的函数关系式;
(2)让s=0,可求出列车从减速开始到列车停止的时间,然后将t=31代入s=t2-16t+256,即可求最后一秒钟,列车滑行的距离.
(1)
解:描点连线如下图:
( http: / / www.21cnjy.com / )
由这条曲线的形状可知,它可能是二次函数的函数的图象;
设s=at2+bt+c(a≠0),因为t=0 ( http: / / www.21cnjy.com )时,s=256,所以c=256,则s=at2+bt+256,将点(4,196),(8,144)代入s=at2+bt+256,得:
,
解这个方程组得:,
∴s=t2-16t+256,
当t=12时,×122-16×12+256=100,
当t=16时,×162-16×16+256=64,
当t=20时,×202-16×20+256=36,
当t=24时,×242-16×24+256=16,
∴其余几对值代入求出的解析式,发现它们都满足该函数解析式,
∴结论:减速阶段列车离停车线的距离s(米)与减速时间t(秒)的函数关系式为s=t2-16t+256(t≥0);
(2)
∵列车停止,
∴s=0,
∴t2-16t+256=0,
解这个方程得:t=32,
∴列车从减速开始经过32秒,列车停止;
∴最后一秒钟时31秒,
当t=31时,×312-16×31+256=0.25,
∴最后一秒钟,列车滑行的距离为0.25米.
【点睛】
本题考查了二次函数的性质,二元一次方程组的解法、一元二次方程的解法,做题的关键是确定二次函数的解析式.
5、 (1)
(2)或
(3)或
【解析】
【分析】
(1)根据抛物线的解析式令即可求得的坐标,令即可求得点的坐标,进而待定系数法求得直线的解析式;
(2)由(1)设点,则在上,代入解方程即可求得的值,进而求得点的值;
(3)先求得直线的解析式,进而表示出解析式,得点的坐标为,进而根据平行得,根据相似三角形的性质可得,根据勾股定理及逆定理证明是直角三角形,进而可得对称后的点与重合,进而可得,求得点的纵坐标,进而根据求得的值,即可求得点的坐标.
(1)
解:已知抛物线交x轴于A,B两点,交y轴于点C,
令,得
即
令,即
解得
设直线的解析式为,将点代入得,
解得
直线的解析式为
(2)
点P是直线上一动点,直线的解析式为
设点,
点P关于原点O的对称点Q刚好落在抛物线上,
则在上
即
解得
或
或
(3)
依题意,设点,
设直线的解析式为,将点代入得,
解得
直线的解析式为
PEBC
设直线的解析式为
令,,则点的坐标为
,,
PEBC
是直角三角形
将沿对折,点P的对应点恰好落在x轴上时,
,
与点重合,
则
,
解得
或
即或
解得或
或
( http: / / www.21cnjy.com / )
【点睛】
本题考查了二次函数与坐标轴交点问题,轴对称问题,相似三角形的性质与判定,勾股定理及其逆定理,一次函数的平移问题,设参数求解是解题的关键.www-2-1-cnjy-com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学下册第三十章二次函数单元测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题 ( http: / / www.21cnjy.com )目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21*cnjy*com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x … -3 -2 -1 0 1 …
y … -6 0 4 6 6 …
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的右侧;
③抛物线的开口向下;
④抛物线与x轴有且只有1个公共点.
以上说法正确是( )
A.① B.①② C.①②③ D.①②③④
2、将关于x的二次函数的图像向上平移1单位,得到的抛物线经过三点、、,则、、的大小关系是( )2-1-c-n-j-y
A. B. C. D.
3、下列实际问题中的y与x之间的函数表达式是二次函数的是( )
A.正方体集装箱的体积,棱长xm
B.小莉驾车以的速度从南京出发到上海,行驶xh,距上海ykm
C.妈妈买烤鸭花费86元,烤鸭的重量y斤,单价为x元/斤
D.高为14m的圆柱形储油罐的体积,底面圆半径xm
4、抛物线,,的图象开口最大的是( )
A. B. C. D.无法确定
5、抛物线y=﹣2(x﹣3)2﹣4的对称轴是( )
A.直线x=3 B.直线x=﹣3 C.直线x=4 D.直线x=﹣4
6、如图,抛物线与轴交于点,对称轴为直线,则下列结论中正确的是( )
( http: / / www.21cnjy.com / )
A.
B.当时,随的增大而增大
C.
D.是一元二次方程的一个根
7、在同一坐标系内,函数y=kx2和y=kx﹣2(k≠0)的图象大致如图( )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )
C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
8、已知二次函数的图象如图所示,根据图中提供的信息,可求得使成立的x的取值范围是( )21*cnjy*com
( http: / / www.21cnjy.com / )
A. B. C. D.或
9、将抛物线向下平移1个单位长度,再向左平移2个单位长度后,得到的抛物线表达式是( )21教育名师原创作品
A. B. C. D.
10、二次函数y=ax2+bx ( http: / / www.21cnjy.com )+c(a≠0)的图象的一部分如图所示,已知图像经过点(﹣1,0),其对称轴为直线x=1.下列结论:①abc<0;②b2﹣4ac<0;③8a+c<0;④若抛物线经过点(﹣3,n),则关于x的一元二次方程ax2+bx+c﹣n=0(a≠0)的两根分别为﹣3,5.上述结论中正确个数有( )
( http: / / www.21cnjy.com / )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c过点(﹣1,﹣4),则下列结论:①对于任意的x=m,均有am2+bm+c≥﹣6;②ac>0;③若点(),(,y2)在抛物线上,则y1>y2;④关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1;⑤b﹣6a=0;其中正确的有_______(填序号).【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
2、对于二次函数与,其自变量与函数值的两组对应值如下表所示,根据二次函数图象的相关性质可知______,______
x ﹣1
c c
d
3、抛物线的顶点坐标是______.
4、已知抛物线经过点.若点在该抛物线上,且,则n的取值范围为______.
5、二次函数y=ax2+bx+c的部分对应值列表如下:
x … ﹣3 0 1 3 5 …
y … 7 ﹣8 ﹣9 ﹣5 7 …
则一元二次方程a(2x+1)2+b(2x+1)+c=﹣5的解为 _____.
三、解答题(5小题,每小题10分,共计50分)
1、图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m.以O为原点,OA所在直线为x轴建立直角坐标系,若点P的坐标为.
( http: / / www.21cnjy.com / )
(1)求拱桥所在抛物线的函数表达式;
(2)因降暴雨水位上升1m,此时水面宽为多少?(结果保留根号)
2、在平面直角坐标系中,二次函 ( http: / / www.21cnjy.com )数y=﹣x2+bx+c的图象经过点(2,3),且交x轴于A(﹣1,0)、B(m,0),求m的值及二次函数图象的对称轴.
3、已知一抛物线的顶点为(2,4),图象过点(1,3).
(1)求抛物线的解析式;
(2)动点P(x,5)能否在抛物线上?请说明理由;
(3)若点A(a,y1),B(b,y2)都在抛物线上,且a<b<0,比较y1,y2的大小,并说明理由.
4、阅读理解,并完成相应的问题.
如图,重庆轨道2号线是中国 ( http: / / www.21cnjy.com )西部地区第一条城市轨道交通线路,也是中国第一条跨座式单轨线路,因其列车在李子坝站穿楼而过闻名全国.小军了解到列车从牛角沱站开往李子坝站时,在距离停车线256米处开始减速.他想知道列车从减速开始,经过多少秒停下来,以及最后一秒滑行的距离.为了解决这个问题,小军通过建立函数模型来描述列车离停车线的距离s(米)与滑行时间t(秒)的函数关系,再应用该函数解决相应的问题.
( http: / / www.21cnjy.com / )
(1)建立模型
①收集数据:
r(秒) 0 4 8 12 16 20 24 ……
s(米) 256 196 144 100 64 36 16 ……
②建立平面直角坐标系为了观察s(米)与t(秒)的关系,建立如图所示的平面直角坐标系.
③描点连线:请在平面直角坐标系中将表中未描出的点补充完整,并用平滑的曲线依次连接.
④选择函数模型:观察这条曲线的形状,它可能是_______函数的图象.
⑤求函数解析式;
解:设,因为时,,所以,则.
请根据表格中的数据,求a,b的值.(请写出详细解答过程).
( http: / / www.21cnjy.com / )
验证:把a,b的值代入中,并将其余几对值代入求出的解析式,发现它们_______满足该函数解析式.(填“都”或“不都”)21教育网
结论:减速阶段列车离停车线的距离s(米)与减速时间t(秒)的函数关系式为__________.
(2)应用模型
列车从减速开始经过_______秒,列车停止;最后一秒钟,列车滑行的距离为_______米.
5、如图1,已知抛物线交x轴于A,B两点,交y轴于点C,点P是直线上一动点.
( http: / / www.21cnjy.com / )
(1)求直线的解析式;
(2)若点P关于原点O的对称点Q刚好落在抛物线上,求点P的坐标;
(3)如图2,连接,过点P作PEBC交x轴于点E,连接,将沿对折,点P的对应点恰好落在x轴上时,求点E的坐标.【版权所有:21教育】
-参考答案-
一、单选题
1、C
【解析】
【分析】
根据表中数据和抛物线的对称性,可得抛物线的对称轴是直线x=,可得到抛物线的开口向下,再根据抛物线的性质即可进行判断.
【详解】
解:根据图表,抛物线与y轴交于(0,6),故①正确;
∵抛物线经过点(0,6)和(1,6),
∴对称轴为x==>0,即抛物线的对称轴在y轴的右侧,故②正确;
当x<时,y随x的增大而增大,
∴抛物线开口向下,故③正确,
∵抛物线经过点(-2,0),
设抛物线经过点(x,0),
∴x==,
解得:x=3,
∴抛物线经过(3,0),即抛物线与x轴有2个交点(-2,0)和(3,0),
故④错误;
综上,正确的有①②③,
故选:C.
【点睛】
本题考查了二次函数及其图象性质,解决问题的关键是注意表格数据的特点,结合二次函数性质作判断.
2、C
【解析】
【分析】
根据题意求得平移后的二次函数的对称轴以及开口方向,根据三个点与对称轴的距离大小判断函数值的大小即可
【详解】
解:∵关于x的二次函数的图像向上平移1单位,得到的抛物线解析式为,
∴新抛物线的对称轴为,开口方向向上,则当抛物线上的点距离对称轴越远,其纵坐标越大,即函数值越大,
平移后的抛物线经过三点、、,
故选C
【点睛】
本题考查了二次函数的平移,二次函数的性质,二次函数的对称轴直线x=,图象具有如下性质:①当a>0时,抛物线的开口向上,x<时,y随x的增大而减小;x>时,y随x的增大而增大;x=时,y取得最小值,即顶点是抛物线的最低点.②当a<0时,抛物线的开口向下,x<时,y随x的增大而增大;x>时,y随x的增大而减小;x=时,y取得最大值,即顶点是抛物线的最高点,掌握二次函数的性质是解题的关键.21·世纪*教育网
3、D
【解析】
【分析】
根据题意,列出关系式,即可判断是否是二次函数.
【详解】
A.由题得:,不是二次函数,故此选项不符合题意;
B.由题得:,不是二次函数,故此选项不符合题意;
C.由题得:,不是二次函数,故此选项不符合题意;
D.由题得:,是二次函数,故此选项符合题意.
故选:D.
【点睛】
本题考查二次函数的定义,形如的形式为二次函数,掌握二次函数的定义是解题的关键.
4、A
【解析】
【分析】
先令x=1,求出函数值,然后再比较二次项系数的绝对值的大小即可解答.
【详解】
解:当x=1时,三条抛物线的对应点是(1,)(1,-3),(1,1),
∵||<|1|<|-3|,
∴抛物线开口最大.
故选A.
【点睛】
本题主要考查了二次函数图象的性质,掌握二次函数解析式的二次项系数的绝对值越小,函数图象的开口越大.
5、A
【解析】
【分析】
直接利用抛物线y=﹣2(x﹣3)2﹣4,求得对称轴方程为:x=3.
【详解】
解:抛物线y=﹣2(x﹣3)2﹣4的对称轴方程为:直线x=3,
故选:A.
【点睛】
本题考查了二次函数的性质与图象,解题的关键是掌握:二次函数的顶点式与对称轴的关系.
6、D
【解析】
【分析】
根据二次函数图象的开口方向向下可得是负数,对称轴位于轴的右侧可得、异号;与轴的交点在正半轴可得是正数,根据二次函数的增减性可得选项错误,根据抛物线的对称轴结合与轴的一个交点的坐标可以求出与轴的另一交点坐标,也就是一元二次方程的根,从而得解.
【详解】
解:、根据图象,二次函数开口方向向下,则,对称轴位于轴的右侧可得、异号,即,故本选项结论错误;21世纪教育网版权所有
B、当时,随的增大而减小,故本选项结论错误;
C、根据图象,抛物线与轴的交点在正半轴,则,故本选项结论错误;
D、抛物线与轴的一个交点坐标是,对称轴是直线,
设另一交点为,
,
,
另一交点坐标是,
是一元二次方程的一个根,
故本选项结论正确.
故选:D.
【点睛】
本题主要考查了二次函数图象与系数的关系,二次函数图象的增减性,抛物线与轴的交点问题,熟记二次函数的性质以及函数图象与系数的关系是解题的关键.2·1·c·n·j·y
7、B
【解析】
【分析】
分别利用函数解析式分析图象得出答案.
【详解】
解:A、二次函数开口向下,k<0;一次函数图象经过第一、三象限,k>0,故此选项错误;
B、两函数图象符合题意;
C、二次函数开口向上,k>0;一次函数图象经过第二、四象限,k<0,故此选项错误;
D、一次函数解析式为:y=kx-2,图象应该与y轴交在负半轴上,故此选项错误.
故选:B.
【点睛】
此题主要考查了二次函数的图象以及一次函数的图象,正确得出k的符号是解题关键.
8、D
【解析】
【分析】
根据函数图象写出y=1对应的自变量x的值,再根据判断范围即可.
【详解】
由图可知,使得时
使成立的x的取值范围是或
故选:D.
【点睛】
本题考查了二次函数与不等式,准确识图是解题的关键.
9、C
【解析】
【分析】
根据平移的规律:左加右减,上加下减可得函数解析式.
【详解】
解:因为y=x2-2x+3=(x-1)2+2.
所以将抛物线y=(x-1)2+2先向下 ( http: / / www.21cnjy.com )平移1个单位长度,再向左平移2个单位长度后,得到的抛物线的表达式为y=(x-1+2)2+2-1,即y=(x+1)2+1.21cnjy.com
故选:C.
【点睛】
本题主要考查了二次函数图象与几何变换,关键是掌握平移的规律.
10、C
【解析】
【分析】
根据图象可判断abc的符号,可判断结论①, ( http: / / www.21cnjy.com )由图象与x轴的交点个数可判断②,由对称轴及x= 2时的函数值即可判断③,由x= 3和对称轴即可判断④.【来源:21cnj*y.co*m】
【详解】
解:∵图象开口向下,
∴a<0,
∵对称轴为直线x=1,
∴ =1,
∴b= 2a>0,
∵图象与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,
∴①说法正确,
由图象可知抛物线与x轴有两个交点,
∴b2 4ac>0,
∴②错误,
由图象可知,当x= 2时,y<0,
∴4a 2b+c=4a 2( 2a)+c=8a+c<0,
∴③正确,
由题意可知x= 3是ax2+bx+c n=0(a≠0)的一个根,
∵对称轴是x=1,
∴另一个根为x=5,
∴④正确,
∴正确的有①③④,
故选:C.
【点睛】
本题主要考查二次函数的图象与性质,关键是要牢记图象与各系数之间的关系.
二、填空题
1、①④⑤
【解析】
【分析】
根据二次函数的开口方向、对称轴、顶点坐标、增减性以及二次函数与一元二次方程的关系综合进行判断即可.
【详解】
解:∵抛物线y=ax2+bx+c的顶点为(﹣3,﹣6),
∴当x=﹣3时,y最小值=﹣6,
∴对于任意的x=m,其函数值y=am2+bm+c≥﹣6,
因此①正确;
∵开口向上,
∴a>0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴ac<0,
因此②不正确;
∵点(),(,y2)在对称轴右侧的抛物线上,根据在对称轴右侧,y随x的增大而增大,
∴y1<y2,
因此③不正确;
∵抛物线y=ax2+bx+c过点(﹣1,﹣4),由对称轴为x=﹣3,根据对称性可知,抛物线y=ax2+bx+c还过点(﹣5,﹣4),21·cn·jy·com
∴当y=﹣4时,即方程ax2+bx+c=﹣4有两个不相等的实数根﹣1和﹣5,
因此④正确;
∵对称轴x=﹣=﹣3,
∴b﹣6a=0,
因此⑤正确;
综上所述,正确的结论有①④⑤,
【点睛】
本题考查了二次函数的开口方向、对称轴、顶点坐标、增减性以及二次函数与一元二次方程的关系综合,掌握二次函数的图象与性质是解题的关键.【出处:21教育名师】
2、 1 3
【解析】
【分析】
根据二次函数的性质可知m=1,将d用含c的式子表示出来即可.
【详解】
解由二次函数的性质可得的对称轴为y轴,故由表可得,
∴m=1;
∵二次函数的对称轴为y轴,
∴d=c+3,
∴3,
故答案为:1,3.
【点睛】
此题考查二次函数的对称性,熟练掌握二次函数的性质是解题的关键.
3、 (2,-1)
【解析】
【分析】
先把抛物线配方为顶点式,再确定顶点坐标即可.
【详解】
解:,
∴抛物线的顶点坐标为(2,-1).
故答案为(2,-1).
【点睛】
本题考查抛物线的顶点坐标,掌握抛物线配方为顶点式的方法是解题关键.
4、
【解析】
【分析】
将点代入求出抛物线的解析式,再求出对称轴为直线,开口向上,自变量离对称轴越远,因变量越大即可求解.www.21-cn-jy.com
【详解】
解:将代入中得到:,
解得,
∴抛物线的对称轴为直线,且开口向上,
根据“自变量离对称轴越远,其对应的因变量越大”可知,
当时,对应的最大为:,
当时,对应的最小为:,
故n的取值范围为:,
故答案为:.
【点睛】
本题考查二次函数的图像及性质,点在抛物线上,将点的坐标代入即可求解.
5、,
【解析】
【分析】
从表中找到三对数值,将三对数值分别代入y=ax2+bx+c组成方程组,求出a、b、c的值,然后再运用因式分解法求解方程即可得到结论.
【详解】
解:将(-3,7),(0,-8),(1,-9)代入y=ax2+bx+c得,
整理得,
②×3+①,得
∴
把代入②得,
∴
又
∴一元二次方程a(2x+1)2+b(2x+1)+c=﹣5可变形为:
即:
∴
∴,或
解得,,
故答案为:,
【点睛】
本题考查了待定系数法求函数解析式和一元二次方程的解法,从图表中找到相关的量是解题的关键.
三、解答题
1、 (1)
(2)
【解析】
【分析】
(1)利用待定系数法求解可得;
(2)在所求函数解析式中求出时的值即可得.
(1)
解:设抛物线的解析式为,
将点、代入,得:,
解得:,
所以抛物线的解析式为;
(2)
当时,,即,
解得:,
则水面的宽为.
【点睛】
本题主要考查二次函数的应用,解题的关键是将实际问题转化为二次函数的问题求解,并熟练掌握待定系数法求函数解析式.
2、m=3,对称轴为直线x=1
【解析】
【分析】
先根据待定系数法求出二次函数的解析式,令y=0求解x即可求得m,进而可求得二次函数图象的对称轴.
【详解】
解:将(2,3)和(-1,0)代入y=﹣x2+bx+c中,
得:,解得:,
∴y=﹣x2+2x+3,
令y=0,则﹣x2+2x+3=0,即x2﹣2x﹣3=0,
解得:x1=-1,x2=3,
∴该二次函数图象与x轴的交点坐标为A(-1,0)和B(3,0),
∴m=3,
该二次函数图象的对称轴为直线x=1.
【点睛】
本题考查待定系数法求二次 ( http: / / www.21cnjy.com )函数解析式、二次函数图象与坐标轴的交点问题、二次函数图象的对称轴,熟练掌握待定系数法求函数解析式的步骤是解答的关键.
3、 (1)
(2)不在,见解析
(3)y1<y2,见解析
【解析】
【分析】
(1)根据已知条件设抛物线的解析式为顶点式,把点(1,3)的坐标代入所设的解析式中即可求得a,从而可求得函数解析式;
(2)把点P的纵坐标代入抛物线的解析式中,得到关于x的二元一次方程,若方程有解,则点P在抛物线,否则不在抛物线上;
(3)抛物线的对称轴为直线x=2,根据抛物线的增减性质即可比较大小.
(1)
设抛物线的解析式为
把点(1,3)的坐标代入中,得a+4=3
∴
即抛物线的解析式为;
(2)
动点P(x,5)不在抛物线上
理由如下:
在中,当y=5时,得
即
此方程无解
故点P不在抛物线上;
(3)
y1<y2
理由如下:
抛物线的对称轴为直线x=2
∵二次项系数 1<0,且
∴函数值随自变量的增大而增大
即y1<y2
【点睛】
本题考查了待定系数法求二次函 ( http: / / www.21cnjy.com )数的解析式,二次函数与一元二次方程的关系,二次函数的图象与性质等知识,熟练掌握这些知识是关键,属于二次函数的基础题目.
4、 (1)二次, 都, s=
(2)32,0.25
【解析】
【分析】
(1)通过描点、连线,观察图形 ( http: / / www.21cnjy.com )可知,图象可能是二次函数的函数的图象;将点(4,196),(8,144)代入s=at2+bt+256,得a、b的值,再将其余几对值代入求出的解析式,发现它们都满足该函数解析式,最后得到结论:减速阶段列车离停车线的距离s(米)与减速时间t(秒)的函数关系式;
(2)让s=0,可求出列车从减速开始到列车停止的时间,然后将t=31代入s=t2-16t+256,即可求最后一秒钟,列车滑行的距离.
(1)
解:描点连线如下图:
( http: / / www.21cnjy.com / )
由这条曲线的形状可知,它可能是二次函数的函数的图象;
设s=at2+bt+c(a≠0),因为t=0 ( http: / / www.21cnjy.com )时,s=256,所以c=256,则s=at2+bt+256,将点(4,196),(8,144)代入s=at2+bt+256,得:
,
解这个方程组得:,
∴s=t2-16t+256,
当t=12时,×122-16×12+256=100,
当t=16时,×162-16×16+256=64,
当t=20时,×202-16×20+256=36,
当t=24时,×242-16×24+256=16,
∴其余几对值代入求出的解析式,发现它们都满足该函数解析式,
∴结论:减速阶段列车离停车线的距离s(米)与减速时间t(秒)的函数关系式为s=t2-16t+256(t≥0);
(2)
∵列车停止,
∴s=0,
∴t2-16t+256=0,
解这个方程得:t=32,
∴列车从减速开始经过32秒,列车停止;
∴最后一秒钟时31秒,
当t=31时,×312-16×31+256=0.25,
∴最后一秒钟,列车滑行的距离为0.25米.
【点睛】
本题考查了二次函数的性质,二元一次方程组的解法、一元二次方程的解法,做题的关键是确定二次函数的解析式.
5、 (1)
(2)或
(3)或
【解析】
【分析】
(1)根据抛物线的解析式令即可求得的坐标,令即可求得点的坐标,进而待定系数法求得直线的解析式;
(2)由(1)设点,则在上,代入解方程即可求得的值,进而求得点的值;
(3)先求得直线的解析式,进而表示出解析式,得点的坐标为,进而根据平行得,根据相似三角形的性质可得,根据勾股定理及逆定理证明是直角三角形,进而可得对称后的点与重合,进而可得,求得点的纵坐标,进而根据求得的值,即可求得点的坐标.
(1)
解:已知抛物线交x轴于A,B两点,交y轴于点C,
令,得
即
令,即
解得
设直线的解析式为,将点代入得,
解得
直线的解析式为
(2)
点P是直线上一动点,直线的解析式为
设点,
点P关于原点O的对称点Q刚好落在抛物线上,
则在上
即
解得
或
或
(3)
依题意,设点,
设直线的解析式为,将点代入得,
解得
直线的解析式为
PEBC
设直线的解析式为
令,,则点的坐标为
,,
PEBC
是直角三角形
将沿对折,点P的对应点恰好落在x轴上时,
,
与点重合,
则
,
解得
或
即或
解得或
或
( http: / / www.21cnjy.com / )
【点睛】
本题考查了二次函数与坐标轴交点问题,轴对称问题,相似三角形的性质与判定,勾股定理及其逆定理,一次函数的平移问题,设参数求解是解题的关键.www-2-1-cnjy-com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
