2022-2023学年苏科版八年级数学上册第1章全等三角形 选择专项练习题(word、含解析)
文档属性
| 名称 | 2022-2023学年苏科版八年级数学上册第1章全等三角形 选择专项练习题(word、含解析) | 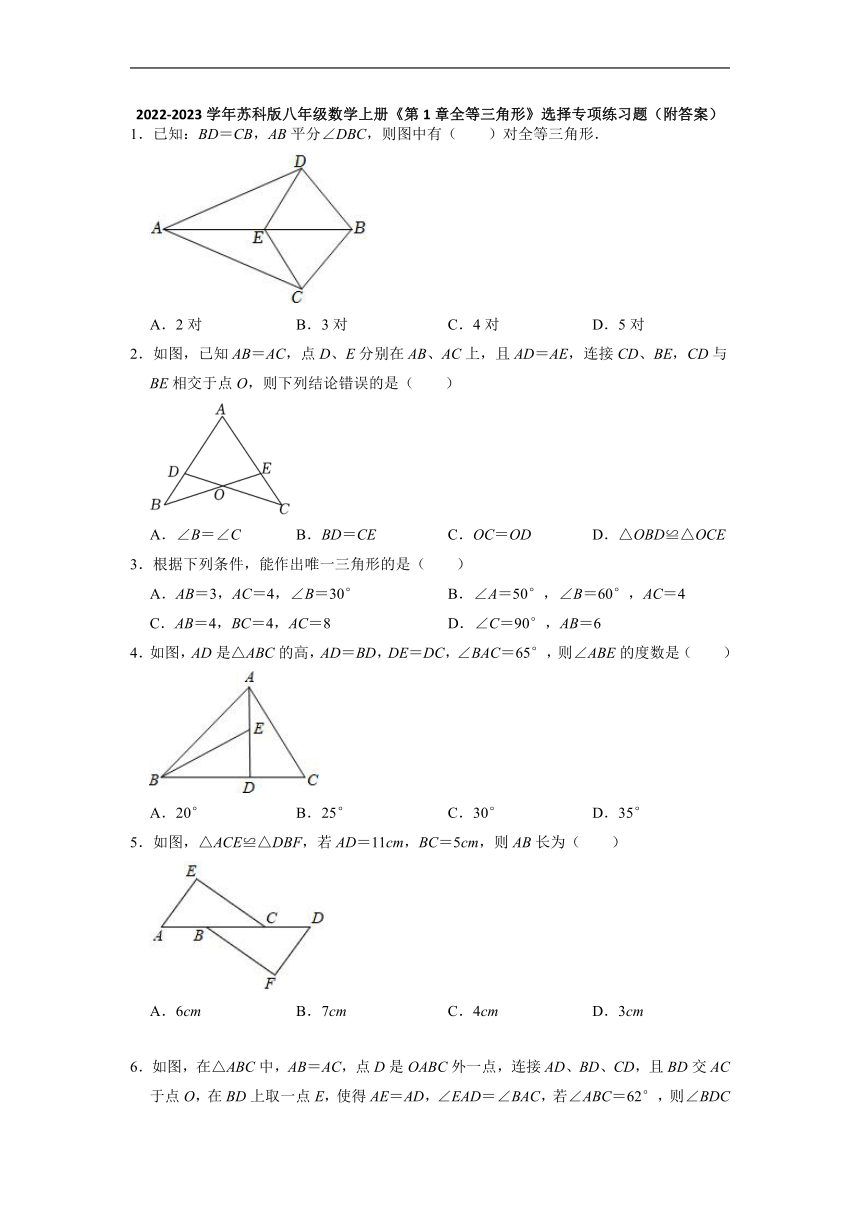 | |
| 格式 | docx | ||
| 文件大小 | 278.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-28 23:19:20 | ||
图片预览




文档简介
2022-2023学年苏科版八年级数学上册《第1章全等三角形》选择专项练习题(附答案)
1.已知:BD=CB,AB平分∠DBC,则图中有( )对全等三角形.
A.2对 B.3对 C.4对 D.5对
2.如图,已知AB=AC,点D、E分别在AB、AC上,且AD=AE,连接CD、BE,CD与BE相交于点O,则下列结论错误的是( )
A.∠B=∠C B.BD=CE C.OC=OD D.△OBD≌△OCE
3.根据下列条件,能作出唯一三角形的是( )
A.AB=3,AC=4,∠B=30° B.∠A=50°,∠B=60°,AC=4
C.AB=4,BC=4,AC=8 D.∠C=90°,AB=6
4.如图,AD是△ABC的高,AD=BD,DE=DC,∠BAC=65°,则∠ABE的度数是( )
A.20° B.25° C.30° D.35°
5.如图,△ACE≌△DBF,若AD=11cm,BC=5cm,则AB长为( )
A.6cm B.7cm C.4cm D.3cm
6.如图,在△ABC中,AB=AC,点D是OABC外一点,连接AD、BD、CD,且BD交AC于点O,在BD上取一点E,使得AE=AD,∠EAD=∠BAC,若∠ABC=62°,则∠BDC的度数为( )
A.56° B.60° C.62° D.64°
7.如图,已知∠C=∠D,AC=AD,增加下列条件:
①AB=AE;②BC=ED;③∠1=∠2;④∠B=∠E.
其中能使△ABC≌△AED的条件有( )
A.4个 B.3个 C.2个 D.1个
8.如图,已知△ABC的面积为16,BP平分∠ABC,且AD⊥BP于点P,则△BPC的面积是( )
A.4 B.6 C.8 D.12
9.如图,点A在DE上,AC=EC,∠1=∠2=∠3,则DE等于( )
A.AB B.BC C.DC D.AE+AC
10.如图,△ABC和△ECD都是等腰直角三角形,△ABC的顶点A在△ECD的斜边DE上.下列结论:①△ACE≌△BCD;②∠DAB=∠ACE;③AE+AC=CD;④△ABD是直角三角形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
11.如图,Rt△ABC中,CD⊥AB于D,E在AC上,过E作EF⊥AB于F,且EF=EC,连接BE交CD于G.结论:
①∠CEB=∠BEF ②CG=EF ③∠BGC=∠AEB ④∠AEF=2∠ABE
以上结论正确的个数是( )
A.1 B.2 C.3 D.4
12.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠BAC的度数为( )
A.90° B.80° C.70° D.60°
13.如图,∠BAD=90°,AC平分∠BAD,CB=CD,则∠B与∠ADC满足的数量关系为( )
A.∠B=∠ADC B.2∠B=∠ADC
C.∠B+∠ADC=180° D.∠B+∠ADC=90°
14.如图,∠ABC=∠ACD=90°,BC=2,AC=CD,则△BCD的面积为( )
A.2 B.4 C. D.6
15.如图,一块玻璃碎成三片,小智只带了第③块去玻璃店,就能配一块一模一样的玻璃,你能用三角形的知识解释,这是为什么?( )
A.ASA B.AAS C.SAS D.SSS
16.如图,在四边形ABCD中,点E在边AD上,∠BCE=∠ACD,∠BAC=∠D=40°,AB=DE,则∠BCE的度数为( )
A.80° B.90° C.100° D.110°
17.如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,下列说法:①CE=BF;②△ABD和△ACD的面积相等;③BF∥CE;④△BDF≌△CDE,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
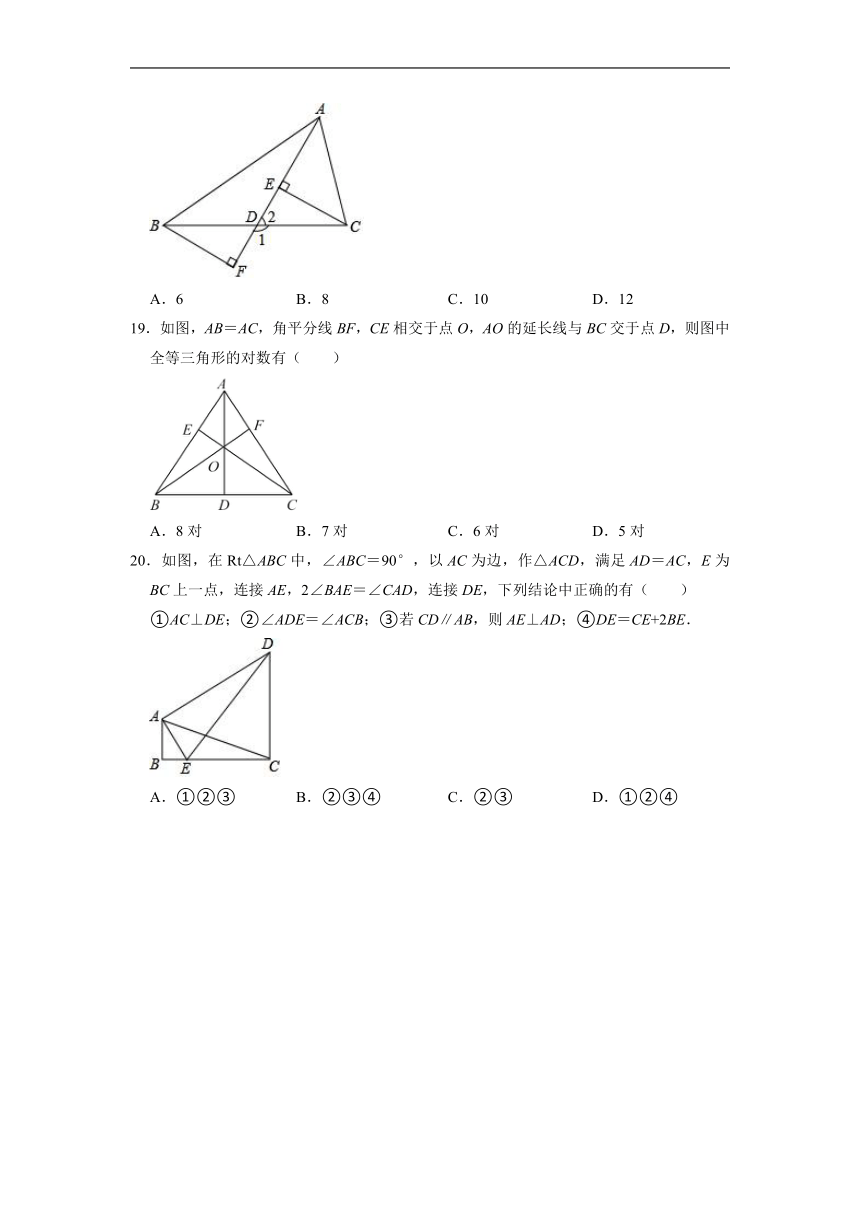
18.如图,AD是△ABC的中线,CE⊥AD,BF⊥AD,点E、F为垂足,若EF=6,∠1=2∠2,则BC的长为( )
A.6 B.8 C.10 D.12
19.如图,AB=AC,角平分线BF,CE相交于点O,AO的延长线与BC交于点D,则图中全等三角形的对数有( )
A.8对 B.7对 C.6对 D.5对
20.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,2∠BAE=∠CAD,连接DE,下列结论中正确的有( )
①AC⊥DE;②∠ADE=∠ACB;③若CD∥AB,则AE⊥AD;④DE=CE+2BE.
A.①②③ B.②③④ C.②③ D.①②④
参考答案
1.解:∵AB平分∠DBC,
∴∠DBA=∠CBA,
∵BD=BC,BA=BA,
∴△BDA≌△BCA(SAS),
∴∠BAD=∠BAC,AD=AC,
∵AE=AE,
∴△AED≌△AEC(SAS),
∴DE=CE,
∵BD=BC,BE=BE,
∴△BDE≌△BCE(SSS),
∴图中一共有3对全等三角形,
故选:B.
2.解:在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠B=∠C,
故A正确,不符合题意;
∵AB=AC,且AD=AE,
∴AB﹣AD=AC﹣AE,
∴BD=CE,
故B正确,不符合题意;
在△OBD和△OCE中,
,
∴△OBD≌△OCE(AAS),
故D正确,不符合题意;
根据题意,证明不出OC=OD,
故C错误,符合题意;
故选:C.
3.解:根据AB=3,AC=4,∠B=30°,无法做出唯一的三角形,故选项A不符合题意;
根据∠A=50°,∠B=60°,AC=4和AAS可以作出唯一的三角形,故选项B符合题意;
∵AB=4,BC=4,AC=8,
∴AB+BC=AC,
∴以4,4,8为边不能组成三角形,故选项C不符合题意;
根据∠C=90°,AB=6,无法做出唯一的三角形,故选项D不符合题意;
故选:B.
4.解:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°,
在△BDE和△ADC中,
,
∴△BDE≌△ADC(SAS),
∴∠DAC=∠DBE,
∵∠DAC=∠BAC﹣∠BAD=65°﹣45°=20°,
∴∠DBE=20°,
∴∠ABE=∠ABD﹣∠DBE=25°,
故选:B.
5.解:∵△ACE≌△DBF,
∴AC=BD,
∴AC﹣BC=BD﹣BC,即AB=CD,
∵AD=11cm,BC=5cm,
∴AB=(11﹣5)÷2=3(cm),
故选:D.
6.解:∵∠EAD=∠BAC,
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC,
即:∠BAE=∠CAD;
在△ABE和△ACD中,
,
∴△ABE≌△ACD (SAS),
∴∠ABD=∠ACD,
∵∠BOC是△ABO和△DCO的外角,
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC,
∴∠ABD+∠BAC=∠ACD+∠BDC,
∴∠BAC=∠BDC,
∵∠ABC=∠ACB=62°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣62°﹣62°=56°,
∴∠BDC=∠BAC=56°,
故选:A.
7.解:①∵∠C=∠D,AC=AD,AB=AE,
∴△ABC和△AED不一定全等,
故①不符合题意;
②∵∠C=∠D,AC=AD,BC=DE,
∴△ABC≌△AED(SAS),
故②符合题意;
③∵∠1=∠2,
∴∠1+∠EAB=∠2+∠EAB,
∴∠CAB=∠DAE,
∵∠C=∠D,AC=AD,
∴△ABC≌△AED(ASA),
故③符合题意;
④∵∠B=∠E,∠C=∠D,AC=AD,
∴△ABC≌△AED(AAS),
故④符合题意;
所以,增加上列条件,其中能使△ABC≌△AED的条件有3个,
故选:B.
8.解:∵BP平分∠ABC,
∴∠ABP=∠DBP,
∵AP⊥BP,
∴∠APB=∠DPB=90°,
在△APB和△DPB中,
,
∴△APB≌△DPB(ASA),
∴AP=PD,
∴S△APB=S△DPB,S△APC=S△DPC,
∴△BPC的面积=×△ABC的面积=8,
故选:C.
9.解:∵∠1=∠2,
∴∠B=∠D,
∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,
即∠ACB=∠ECD,
在△ACB和△ECD中,
,
∴△ACB≌△ECD(AAS),
∴AB=ED.
故选:A.
10.解:∵△ABC和△ECD都是等腰直角三角形,
∴CA=CB,∠CAB=∠CBA=45°,CD=CE,∠E=∠CDE=45°,
∵∠ACE+∠ACD=∠ACD+∠BCD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),所以①正确;
∵∠DAC=∠E+∠ACE,即∠DAB+∠BAC=∠E+∠ACE,
而∠CAB=∠E=45°,
∴∠DAB=∠ACE,所以②正确;
∵AE+AC>CE,CE=CD,
∴AE+AC>CD,所以③错误;
∵△ACE≌△BCD,
∴∠BDC=∠E=45°,
∵∠CDE=45°,
∴∠ADB=∠ADC+∠BDC=45°+45°=90°,
∴△ADB为直角三角形,所以④正确.
故选:C.
11.解:∵AC⊥BC,EF⊥AB,EF=EC,
∴BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠EFB=∠ECB=90°,
∴∠FEB=∠CEB,故①正确;
或者:在Rt△BEC和Rt△BEF中,
,
∴Rt△BEC≌Rt△BEF(HL),
∴∠FEB=∠CEB,故①正确;
∵∠FEB=∠CEB=90°﹣∠EBF,∠BGD=∠CGE=90°﹣∠GBD,
∴∠CEB=∠CGE,
∴CE=CG,
∵EF=EC,
∴CG=EF,故②正确;
∵∠BGC=180°﹣∠CGE,∠AEB=180°﹣∠CEG,∠CEG=∠CGE,
∴∠BGC=∠AEB,故③正确;
∵∠AEF=90°﹣∠A,∠ABC=90°﹣∠A,
∴∠AEF=∠ABC,
∵∠ABC=2∠ABE,
∴∠AEF=2∠ABE,故④正确.
综上所述:正确的结论有①②③④,共4个,
故选:D.
12.解:∵AD=AE,
∴∠ADC=∠AEB,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴AC=AB,∠CAD=∠BAE=60°,
∴∠B=∠C,
∵∠C=∠1﹣∠CAD=110°﹣60°=50°,
∴∠B=50°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣50°=80°,
故选:B.
13.解:在射线AD上截取AE=AB,连接CE,如图所示:
∵∠BAD=90°,AC平分∠BAD,
∴∠BAC=∠EAC,
在△ABC与△AEC中,
,
∴△ABC≌△AEC(SAS),
∴BC=EC,∠B=∠AEC,
∵CB=CD,
∴CD=CE,
∴∠CDE=∠CED,
∴∠B=∠CDE,
∵∠ADC+∠CDE=180°,
∴∠ADC+∠B=180°.
故选:C.
14.解:过点D作DH⊥BC,交BC的延长线于点H,
∵∠ABC=90°,
∴∠BAC+∠ACB=90°,
∵∠ACD=90°,
∴∠HCD+∠ACB=90°,
∴∠BAC=∠HCD,
在△ABC和△CHD中,
,
∴△ABC≌△CHD(AAS),
∴DH=BC=2,
∴△BCD的面积=×BC×DH=×2×2=2,
故选:A.
15.解:根据三角形全等的判定方法,根据角边角可确定一个全等三角形,
只有第三块玻璃包括了两角和它们的夹边,只有带③去才能配一块完全一样的玻璃,是符合题意的.
故选:A.
16.解:∵∠BCE=∠ACD,
又∵∠BCE=∠BCA+∠ACE,∠ACD=∠DCE+∠ACE,
∴∠BCA=∠DCE,
在△BAC和△EDC中,
,
∴△BAC≌△EDC(AAS),
∴AC=CD,
∴∠CAE=∠D,
∵∠D=40°,
∴∠CAD=40°,
∴∠ACD=180°﹣∠CAD﹣∠D=180°﹣40°﹣40°=100°,
∴∠BCE=∠ACD=100°.
故选:C.
17.解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),故④正确
∴CE=BF,∠F=∠CED,故①正确,
∴BF∥CE,故③正确,
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确,
综上所述,正确的有4个,
故选:D.
18.解:∵∠1=2∠2,∠1+∠2=180°,
∴∠2=60°,
∴∠DCE=30°,
∵AD是△ABC的中线,
∴BD=CD,
∵CE⊥AD,BF⊥AD,
∴∠BFD=∠CED=90°,
∵∠BDF=∠CDE,
∴△BFD≌△CED(AAS),
∴DE=DF,
∵EF=6,
∴DE=DF=3,
∴CD=6,
∴BC=12,
故选:D.
19.解:∵AB=AC,角平分线BF、CE交于点O,
∴AO平分∠BAC,点D为BC的中点,
∴BD=CD,
在△BAD和△CAD中,
,
∴△BAD≌△CAD(SSS),
同理可证:△OBD≌△OCD,△OBE≌△OCF,△OEA≌△OFA,△OBA≌△OCA,△BEC≌△CFB,△ABF≌△ACF,
由上可得,图中共有7对全等的三角形,
故选:B.
20.解:如图,延长EB至G,使BE=BG,设AC与DE交于点M,
∵∠ABC=90°,
∴AB⊥GE,
∴AB垂直平分GE,
∴AG=AE,∠GAB=∠BAE=∠DAC,
∵∠BAE=∠GAE,
∴∠GAE=∠CAD,
∴∠GAE+∠EAC=∠CAD+∠EAC,
∴∠GAC=∠EAD,
在△GAC与△EAD中,
,
∴△GAC≌△EAD(SAS),
∴∠G=∠AED,∠ACB=∠ADE,
∴②是正确的;
∵AG=AE,
∴∠G=∠AEG=∠AED,
∴AE平分∠BED,
当∠BAE=∠EAC时,∠AME=∠ABE=90°,则AC⊥DE,
当∠BAE≠∠EAC时,∠AME≠∠ABE,则无法说明AC⊥DE,
∴①是不正确的;
设∠BAE=x,则∠CAD=2x,
∴∠ACD=∠ADC==90°﹣x,
∵AB∥CD,
∴∠BAC=∠ACD=90°﹣x,
∴∠CAE=∠BAC﹣∠EAB=90°﹣x﹣x=90°﹣2x,
∴∠DAE=∠CAE+∠DAC=90°﹣2x+2x=90°,
∴AE⊥AD,
∴③是正确的;
∵△GAC≌△EAD,
∴CG=DE,
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE,
∴④是正确的,
故选:B.
1.已知:BD=CB,AB平分∠DBC,则图中有( )对全等三角形.
A.2对 B.3对 C.4对 D.5对
2.如图,已知AB=AC,点D、E分别在AB、AC上,且AD=AE,连接CD、BE,CD与BE相交于点O,则下列结论错误的是( )
A.∠B=∠C B.BD=CE C.OC=OD D.△OBD≌△OCE
3.根据下列条件,能作出唯一三角形的是( )
A.AB=3,AC=4,∠B=30° B.∠A=50°,∠B=60°,AC=4
C.AB=4,BC=4,AC=8 D.∠C=90°,AB=6
4.如图,AD是△ABC的高,AD=BD,DE=DC,∠BAC=65°,则∠ABE的度数是( )
A.20° B.25° C.30° D.35°
5.如图,△ACE≌△DBF,若AD=11cm,BC=5cm,则AB长为( )
A.6cm B.7cm C.4cm D.3cm
6.如图,在△ABC中,AB=AC,点D是OABC外一点,连接AD、BD、CD,且BD交AC于点O,在BD上取一点E,使得AE=AD,∠EAD=∠BAC,若∠ABC=62°,则∠BDC的度数为( )
A.56° B.60° C.62° D.64°
7.如图,已知∠C=∠D,AC=AD,增加下列条件:
①AB=AE;②BC=ED;③∠1=∠2;④∠B=∠E.
其中能使△ABC≌△AED的条件有( )
A.4个 B.3个 C.2个 D.1个
8.如图,已知△ABC的面积为16,BP平分∠ABC,且AD⊥BP于点P,则△BPC的面积是( )
A.4 B.6 C.8 D.12
9.如图,点A在DE上,AC=EC,∠1=∠2=∠3,则DE等于( )
A.AB B.BC C.DC D.AE+AC
10.如图,△ABC和△ECD都是等腰直角三角形,△ABC的顶点A在△ECD的斜边DE上.下列结论:①△ACE≌△BCD;②∠DAB=∠ACE;③AE+AC=CD;④△ABD是直角三角形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
11.如图,Rt△ABC中,CD⊥AB于D,E在AC上,过E作EF⊥AB于F,且EF=EC,连接BE交CD于G.结论:
①∠CEB=∠BEF ②CG=EF ③∠BGC=∠AEB ④∠AEF=2∠ABE
以上结论正确的个数是( )
A.1 B.2 C.3 D.4
12.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠BAC的度数为( )
A.90° B.80° C.70° D.60°
13.如图,∠BAD=90°,AC平分∠BAD,CB=CD,则∠B与∠ADC满足的数量关系为( )
A.∠B=∠ADC B.2∠B=∠ADC
C.∠B+∠ADC=180° D.∠B+∠ADC=90°
14.如图,∠ABC=∠ACD=90°,BC=2,AC=CD,则△BCD的面积为( )
A.2 B.4 C. D.6
15.如图,一块玻璃碎成三片,小智只带了第③块去玻璃店,就能配一块一模一样的玻璃,你能用三角形的知识解释,这是为什么?( )
A.ASA B.AAS C.SAS D.SSS
16.如图,在四边形ABCD中,点E在边AD上,∠BCE=∠ACD,∠BAC=∠D=40°,AB=DE,则∠BCE的度数为( )
A.80° B.90° C.100° D.110°
17.如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,下列说法:①CE=BF;②△ABD和△ACD的面积相等;③BF∥CE;④△BDF≌△CDE,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
18.如图,AD是△ABC的中线,CE⊥AD,BF⊥AD,点E、F为垂足,若EF=6,∠1=2∠2,则BC的长为( )
A.6 B.8 C.10 D.12
19.如图,AB=AC,角平分线BF,CE相交于点O,AO的延长线与BC交于点D,则图中全等三角形的对数有( )
A.8对 B.7对 C.6对 D.5对
20.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,2∠BAE=∠CAD,连接DE,下列结论中正确的有( )
①AC⊥DE;②∠ADE=∠ACB;③若CD∥AB,则AE⊥AD;④DE=CE+2BE.
A.①②③ B.②③④ C.②③ D.①②④
参考答案
1.解:∵AB平分∠DBC,
∴∠DBA=∠CBA,
∵BD=BC,BA=BA,
∴△BDA≌△BCA(SAS),
∴∠BAD=∠BAC,AD=AC,
∵AE=AE,
∴△AED≌△AEC(SAS),
∴DE=CE,
∵BD=BC,BE=BE,
∴△BDE≌△BCE(SSS),
∴图中一共有3对全等三角形,
故选:B.
2.解:在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠B=∠C,
故A正确,不符合题意;
∵AB=AC,且AD=AE,
∴AB﹣AD=AC﹣AE,
∴BD=CE,
故B正确,不符合题意;
在△OBD和△OCE中,
,
∴△OBD≌△OCE(AAS),
故D正确,不符合题意;
根据题意,证明不出OC=OD,
故C错误,符合题意;
故选:C.
3.解:根据AB=3,AC=4,∠B=30°,无法做出唯一的三角形,故选项A不符合题意;
根据∠A=50°,∠B=60°,AC=4和AAS可以作出唯一的三角形,故选项B符合题意;
∵AB=4,BC=4,AC=8,
∴AB+BC=AC,
∴以4,4,8为边不能组成三角形,故选项C不符合题意;
根据∠C=90°,AB=6,无法做出唯一的三角形,故选项D不符合题意;
故选:B.
4.解:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°,
在△BDE和△ADC中,
,
∴△BDE≌△ADC(SAS),
∴∠DAC=∠DBE,
∵∠DAC=∠BAC﹣∠BAD=65°﹣45°=20°,
∴∠DBE=20°,
∴∠ABE=∠ABD﹣∠DBE=25°,
故选:B.
5.解:∵△ACE≌△DBF,
∴AC=BD,
∴AC﹣BC=BD﹣BC,即AB=CD,
∵AD=11cm,BC=5cm,
∴AB=(11﹣5)÷2=3(cm),
故选:D.
6.解:∵∠EAD=∠BAC,
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC,
即:∠BAE=∠CAD;
在△ABE和△ACD中,
,
∴△ABE≌△ACD (SAS),
∴∠ABD=∠ACD,
∵∠BOC是△ABO和△DCO的外角,
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC,
∴∠ABD+∠BAC=∠ACD+∠BDC,
∴∠BAC=∠BDC,
∵∠ABC=∠ACB=62°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣62°﹣62°=56°,
∴∠BDC=∠BAC=56°,
故选:A.
7.解:①∵∠C=∠D,AC=AD,AB=AE,
∴△ABC和△AED不一定全等,
故①不符合题意;
②∵∠C=∠D,AC=AD,BC=DE,
∴△ABC≌△AED(SAS),
故②符合题意;
③∵∠1=∠2,
∴∠1+∠EAB=∠2+∠EAB,
∴∠CAB=∠DAE,
∵∠C=∠D,AC=AD,
∴△ABC≌△AED(ASA),
故③符合题意;
④∵∠B=∠E,∠C=∠D,AC=AD,
∴△ABC≌△AED(AAS),
故④符合题意;
所以,增加上列条件,其中能使△ABC≌△AED的条件有3个,
故选:B.
8.解:∵BP平分∠ABC,
∴∠ABP=∠DBP,
∵AP⊥BP,
∴∠APB=∠DPB=90°,
在△APB和△DPB中,
,
∴△APB≌△DPB(ASA),
∴AP=PD,
∴S△APB=S△DPB,S△APC=S△DPC,
∴△BPC的面积=×△ABC的面积=8,
故选:C.
9.解:∵∠1=∠2,
∴∠B=∠D,
∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,
即∠ACB=∠ECD,
在△ACB和△ECD中,
,
∴△ACB≌△ECD(AAS),
∴AB=ED.
故选:A.
10.解:∵△ABC和△ECD都是等腰直角三角形,
∴CA=CB,∠CAB=∠CBA=45°,CD=CE,∠E=∠CDE=45°,
∵∠ACE+∠ACD=∠ACD+∠BCD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),所以①正确;
∵∠DAC=∠E+∠ACE,即∠DAB+∠BAC=∠E+∠ACE,
而∠CAB=∠E=45°,
∴∠DAB=∠ACE,所以②正确;
∵AE+AC>CE,CE=CD,
∴AE+AC>CD,所以③错误;
∵△ACE≌△BCD,
∴∠BDC=∠E=45°,
∵∠CDE=45°,
∴∠ADB=∠ADC+∠BDC=45°+45°=90°,
∴△ADB为直角三角形,所以④正确.
故选:C.
11.解:∵AC⊥BC,EF⊥AB,EF=EC,
∴BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠EFB=∠ECB=90°,
∴∠FEB=∠CEB,故①正确;
或者:在Rt△BEC和Rt△BEF中,
,
∴Rt△BEC≌Rt△BEF(HL),
∴∠FEB=∠CEB,故①正确;
∵∠FEB=∠CEB=90°﹣∠EBF,∠BGD=∠CGE=90°﹣∠GBD,
∴∠CEB=∠CGE,
∴CE=CG,
∵EF=EC,
∴CG=EF,故②正确;
∵∠BGC=180°﹣∠CGE,∠AEB=180°﹣∠CEG,∠CEG=∠CGE,
∴∠BGC=∠AEB,故③正确;
∵∠AEF=90°﹣∠A,∠ABC=90°﹣∠A,
∴∠AEF=∠ABC,
∵∠ABC=2∠ABE,
∴∠AEF=2∠ABE,故④正确.
综上所述:正确的结论有①②③④,共4个,
故选:D.
12.解:∵AD=AE,
∴∠ADC=∠AEB,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴AC=AB,∠CAD=∠BAE=60°,
∴∠B=∠C,
∵∠C=∠1﹣∠CAD=110°﹣60°=50°,
∴∠B=50°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣50°=80°,
故选:B.
13.解:在射线AD上截取AE=AB,连接CE,如图所示:
∵∠BAD=90°,AC平分∠BAD,
∴∠BAC=∠EAC,
在△ABC与△AEC中,
,
∴△ABC≌△AEC(SAS),
∴BC=EC,∠B=∠AEC,
∵CB=CD,
∴CD=CE,
∴∠CDE=∠CED,
∴∠B=∠CDE,
∵∠ADC+∠CDE=180°,
∴∠ADC+∠B=180°.
故选:C.
14.解:过点D作DH⊥BC,交BC的延长线于点H,
∵∠ABC=90°,
∴∠BAC+∠ACB=90°,
∵∠ACD=90°,
∴∠HCD+∠ACB=90°,
∴∠BAC=∠HCD,
在△ABC和△CHD中,
,
∴△ABC≌△CHD(AAS),
∴DH=BC=2,
∴△BCD的面积=×BC×DH=×2×2=2,
故选:A.
15.解:根据三角形全等的判定方法,根据角边角可确定一个全等三角形,
只有第三块玻璃包括了两角和它们的夹边,只有带③去才能配一块完全一样的玻璃,是符合题意的.
故选:A.
16.解:∵∠BCE=∠ACD,
又∵∠BCE=∠BCA+∠ACE,∠ACD=∠DCE+∠ACE,
∴∠BCA=∠DCE,
在△BAC和△EDC中,
,
∴△BAC≌△EDC(AAS),
∴AC=CD,
∴∠CAE=∠D,
∵∠D=40°,
∴∠CAD=40°,
∴∠ACD=180°﹣∠CAD﹣∠D=180°﹣40°﹣40°=100°,
∴∠BCE=∠ACD=100°.
故选:C.
17.解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),故④正确
∴CE=BF,∠F=∠CED,故①正确,
∴BF∥CE,故③正确,
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确,
综上所述,正确的有4个,
故选:D.
18.解:∵∠1=2∠2,∠1+∠2=180°,
∴∠2=60°,
∴∠DCE=30°,
∵AD是△ABC的中线,
∴BD=CD,
∵CE⊥AD,BF⊥AD,
∴∠BFD=∠CED=90°,
∵∠BDF=∠CDE,
∴△BFD≌△CED(AAS),
∴DE=DF,
∵EF=6,
∴DE=DF=3,
∴CD=6,
∴BC=12,
故选:D.
19.解:∵AB=AC,角平分线BF、CE交于点O,
∴AO平分∠BAC,点D为BC的中点,
∴BD=CD,
在△BAD和△CAD中,
,
∴△BAD≌△CAD(SSS),
同理可证:△OBD≌△OCD,△OBE≌△OCF,△OEA≌△OFA,△OBA≌△OCA,△BEC≌△CFB,△ABF≌△ACF,
由上可得,图中共有7对全等的三角形,
故选:B.
20.解:如图,延长EB至G,使BE=BG,设AC与DE交于点M,
∵∠ABC=90°,
∴AB⊥GE,
∴AB垂直平分GE,
∴AG=AE,∠GAB=∠BAE=∠DAC,
∵∠BAE=∠GAE,
∴∠GAE=∠CAD,
∴∠GAE+∠EAC=∠CAD+∠EAC,
∴∠GAC=∠EAD,
在△GAC与△EAD中,
,
∴△GAC≌△EAD(SAS),
∴∠G=∠AED,∠ACB=∠ADE,
∴②是正确的;
∵AG=AE,
∴∠G=∠AEG=∠AED,
∴AE平分∠BED,
当∠BAE=∠EAC时,∠AME=∠ABE=90°,则AC⊥DE,
当∠BAE≠∠EAC时,∠AME≠∠ABE,则无法说明AC⊥DE,
∴①是不正确的;
设∠BAE=x,则∠CAD=2x,
∴∠ACD=∠ADC==90°﹣x,
∵AB∥CD,
∴∠BAC=∠ACD=90°﹣x,
∴∠CAE=∠BAC﹣∠EAB=90°﹣x﹣x=90°﹣2x,
∴∠DAE=∠CAE+∠DAC=90°﹣2x+2x=90°,
∴AE⊥AD,
∴③是正确的;
∵△GAC≌△EAD,
∴CG=DE,
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE,
∴④是正确的,
故选:B.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
