2022-2023学年人教版八年级数学上册11.2与三角形有关的角 课时练习(word版含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册11.2与三角形有关的角 课时练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 705.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-28 22:51:58 | ||
图片预览


文档简介
11.2与三角形有关的角
一、单选题
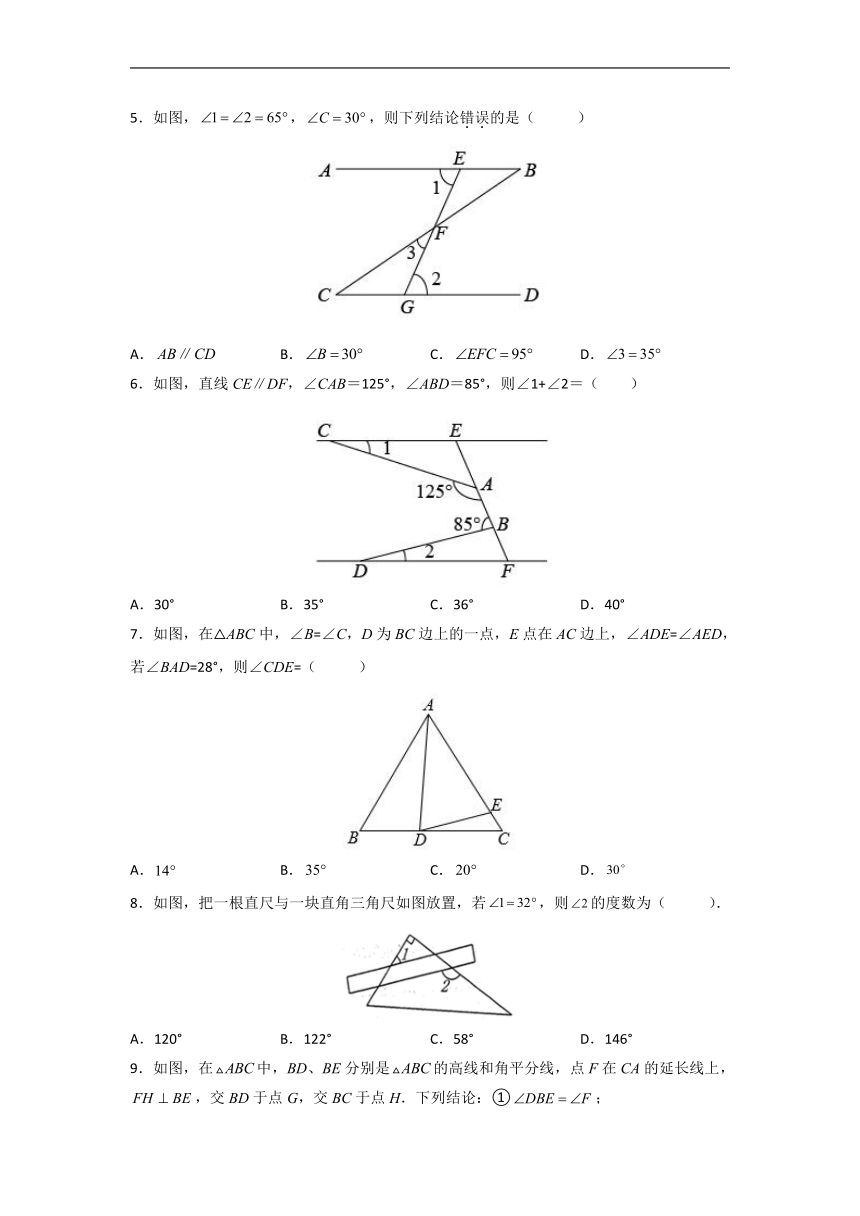
1.如图,在中,平分,则的度数是( )
A. B. C. D.
2.如图,把△ABC纸片沿MN折叠,使点C落在△ABC内部点C′处,若∠C=36°,则∠1+∠2等于( )
A.54° B.62° C.72° D.76°
3.如图,,,,则的大小是( )
A.38° B.48° C.58° D.68°
4.将一副三角板如图摆放,顶点在边上,顶点在边上,,则的度数为( )
A. B. C. D.
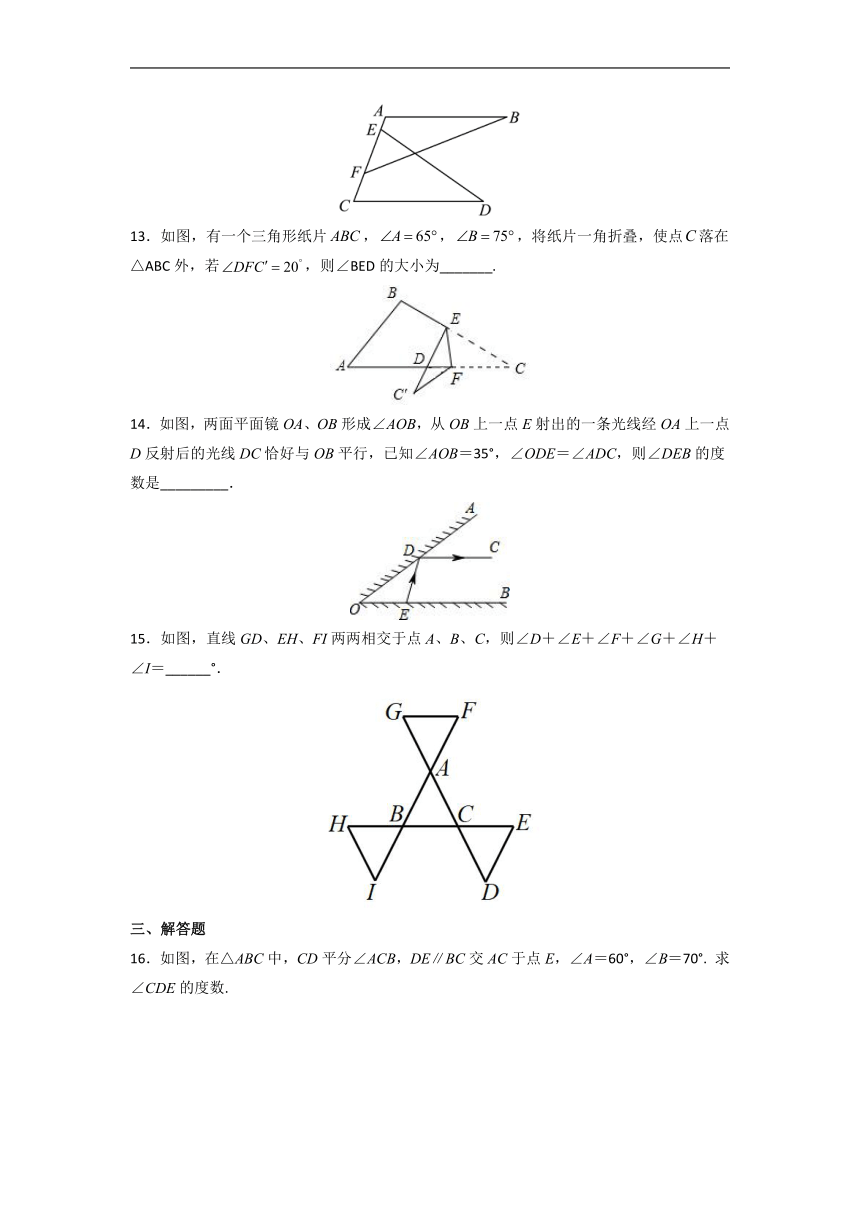
5.如图,,,则下列结论错误的是( )
A. B. C. D.
6.如图,直线CE∥DF,∠CAB=125°,∠ABD=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
7.如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=28°,则∠CDE=( )
A. B. C. D.
8.如图,把一根直尺与一块直角三角尺如图放置,若,则的度数为( ).
A.120° B.122° C.58° D.146°
9.如图,在中,BD、BE分别是的高线和角平分线,点F在CA的延长线上,,交BD于点G,交BC于点H.下列结论:①;②;③;④,其中正确有( )个
A.1个 B.2个 C.3个 D.4个
10.如图,已知的内角,分别作内角与外角的平分线,两条平分线交于点,得;和的平分线交于点,得;……以此类推得到,则的度数是( )
A. B. C. D.
二、填空题
11.如图,点D,E分别在线段,上,连接,.若,,,则的大小为_______.
12.如图,AB∥CD,点E、F在AC边上,已知∠CED=70°,∠BFC=130°,则∠B+∠D的度数为______.
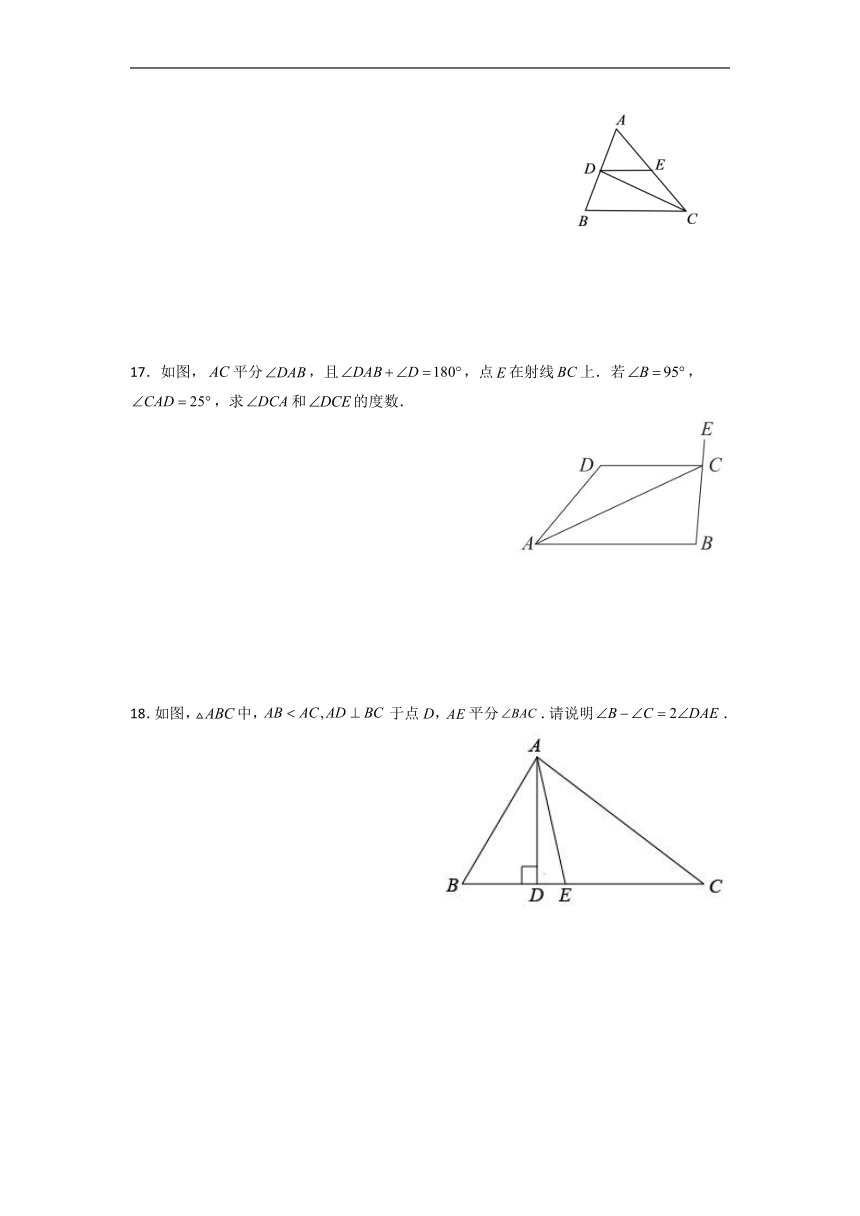
13.如图,有一个三角形纸片,,,将纸片一角折叠,使点落在△ABC外,若,则∠BED的大小为_______.
14.如图,两面平面镜OA、OB形成∠AOB,从OB上一点E射出的一条光线经OA上一点D反射后的光线DC恰好与OB平行,已知∠AOB=35°,∠ODE=∠ADC,则∠DEB的度数是_________.
15.如图,直线GD、EH、FI两两相交于点A、B、C,则∠D+∠E+∠F+∠G+∠H+∠I=______°.
三、解答题
16.如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于点E,∠A=60°,∠B=70°. 求∠CDE的度数.
17.如图,平分,且,点在射线上.若,,求和的度数.
18.如图,中,于点D,平分.请说明.
19.如图,在△ABC中,∠A=68°,∠ABC=60°,CD平分∠ACB.
(1)在△ABC中画出AC边上的高BE,交CD于点O;
(2)求∠BOC和∠ABE的度数.
20.如图,在△ABC中,∠ABC=42 ,∠C=78 ,AD平分∠BAC.
(1)求∠ADC的度数;
(2)在△ABD中分别画出BD边和AD边上的高AE、BF,试说明∠DAE=∠DBF,并求∠DAE的度数;
(3)试探究∠DAE与∠ABC,∠C之间的数量关系,写出你的结论.(不必写理由)
21.某同学在学习过程中,对教材的一个有趣的问题做如下探究:
【习题回顾】
已知:如图1,在△ABC中,角平分线BO、CO交于点O.求∠BOC的度数.
(1)若∠A=40 ,请直接写出∠BOC=________;
(2)【变式思考】若∠A=α,请猜想与的关系,并说明理由;
(3)【拓展延伸】已知:如图2,在△ABC中,角平分线BO、CO交于点O,OD⊥OB,交边BC于点D,作∠ABE的平分线交CO的延长线于点F.若∠F=β,猜想∠BAC与β的关系,并说明理由.
参考答案
一、单选题:1—10 ACCAC AABDB
二、填空题:
11.70° 12.60° 13.100° 14.70° 15.360
三、解答题:
16.解:在△ABC中,∠A=60°,∠B=70°,
∴∠ACB=180°﹣∠A﹣∠B=50°,
∵CD平分∠ACB,
∴∠BCD=∠ACD=∠ACB=25°,
又∵DE∥BC,
∴∠CDE=∠BCD=25°,
答:∠CDE的度数为25°.
17.∵∠DAB+∠D=180°,
∴CD∥AB,
∴∠DCE=∠B=95°,
∵∠CAD=25°,AC平分∠DAB,
∴∠CAB=∠CAD=25°,∠DAB=2∠CAD=50°,
∴∠D=180°-∠DAB=130°,
∴∠DCA=180°-∠D-∠CAD=25°.
18.证明:∵平分,
∴∠BAE=,
∵,
∴∠ADB=90°,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=,
∴.
19.(1)解:如图1,为边上的高.
(2)解:,
,
平分,
,
为边上的高,
,
,
,
.
20.(1)解:∵ ∠ABC=42°, ∠C=78°,
∴ ∠BAC=180°-∠ABC-∠C=60°.
∵ AD平分∠BAC,
∴ ∠BAD=∠BAC=30°.
∴ ∠ADC=∠ABC+∠BAD=42°+30°=72°.
(2)解:如图1所示,AE为BD边上的高,BF为AD边上的高.
在△ADE和△BFD中,
∵ ∠AED=∠BFD=90°,∠ADE=∠BDF,
∴ ∠DAE=∠DBF.
∴ ∠DAE=180°-∠AED-∠ADE =180°-90°-72°=18°.
(3)解:∠DAE=(∠C-∠ABC),
理由如下:∵∠ADE是△ABD的外角,
∴∠ADE=∠ABC+∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠BAC=(180°-∠ABC-∠C),
∴∠ADE=∠ABD+∠BAD=∠ABC+(180°-∠ABC-∠C)=90°+∠ABC-∠C,
∵AE⊥BC,
∴∠AED=90°,
∴∠DAE=90°-∠ADE=90°-(90°+∠ABC-∠C)=∠C-∠ABC=(∠C-∠ABC),
即∠DAE=(∠C-∠ABC).
21.(1)110°,
(2)∵,
∴,
∵、是角平分线,
∴,
∴,
(3)
由图可知
∵,
∴,
∴,
∴,
∴,
∴.
一、单选题
1.如图,在中,平分,则的度数是( )
A. B. C. D.
2.如图,把△ABC纸片沿MN折叠,使点C落在△ABC内部点C′处,若∠C=36°,则∠1+∠2等于( )
A.54° B.62° C.72° D.76°
3.如图,,,,则的大小是( )
A.38° B.48° C.58° D.68°
4.将一副三角板如图摆放,顶点在边上,顶点在边上,,则的度数为( )
A. B. C. D.
5.如图,,,则下列结论错误的是( )
A. B. C. D.
6.如图,直线CE∥DF,∠CAB=125°,∠ABD=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
7.如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=28°,则∠CDE=( )
A. B. C. D.
8.如图,把一根直尺与一块直角三角尺如图放置,若,则的度数为( ).
A.120° B.122° C.58° D.146°
9.如图,在中,BD、BE分别是的高线和角平分线,点F在CA的延长线上,,交BD于点G,交BC于点H.下列结论:①;②;③;④,其中正确有( )个
A.1个 B.2个 C.3个 D.4个
10.如图,已知的内角,分别作内角与外角的平分线,两条平分线交于点,得;和的平分线交于点,得;……以此类推得到,则的度数是( )
A. B. C. D.
二、填空题
11.如图,点D,E分别在线段,上,连接,.若,,,则的大小为_______.
12.如图,AB∥CD,点E、F在AC边上,已知∠CED=70°,∠BFC=130°,则∠B+∠D的度数为______.
13.如图,有一个三角形纸片,,,将纸片一角折叠,使点落在△ABC外,若,则∠BED的大小为_______.
14.如图,两面平面镜OA、OB形成∠AOB,从OB上一点E射出的一条光线经OA上一点D反射后的光线DC恰好与OB平行,已知∠AOB=35°,∠ODE=∠ADC,则∠DEB的度数是_________.
15.如图,直线GD、EH、FI两两相交于点A、B、C,则∠D+∠E+∠F+∠G+∠H+∠I=______°.
三、解答题
16.如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于点E,∠A=60°,∠B=70°. 求∠CDE的度数.
17.如图,平分,且,点在射线上.若,,求和的度数.
18.如图,中,于点D,平分.请说明.
19.如图,在△ABC中,∠A=68°,∠ABC=60°,CD平分∠ACB.
(1)在△ABC中画出AC边上的高BE,交CD于点O;
(2)求∠BOC和∠ABE的度数.
20.如图,在△ABC中,∠ABC=42 ,∠C=78 ,AD平分∠BAC.
(1)求∠ADC的度数;
(2)在△ABD中分别画出BD边和AD边上的高AE、BF,试说明∠DAE=∠DBF,并求∠DAE的度数;
(3)试探究∠DAE与∠ABC,∠C之间的数量关系,写出你的结论.(不必写理由)
21.某同学在学习过程中,对教材的一个有趣的问题做如下探究:
【习题回顾】
已知:如图1,在△ABC中,角平分线BO、CO交于点O.求∠BOC的度数.
(1)若∠A=40 ,请直接写出∠BOC=________;
(2)【变式思考】若∠A=α,请猜想与的关系,并说明理由;
(3)【拓展延伸】已知:如图2,在△ABC中,角平分线BO、CO交于点O,OD⊥OB,交边BC于点D,作∠ABE的平分线交CO的延长线于点F.若∠F=β,猜想∠BAC与β的关系,并说明理由.
参考答案
一、单选题:1—10 ACCAC AABDB
二、填空题:
11.70° 12.60° 13.100° 14.70° 15.360
三、解答题:
16.解:在△ABC中,∠A=60°,∠B=70°,
∴∠ACB=180°﹣∠A﹣∠B=50°,
∵CD平分∠ACB,
∴∠BCD=∠ACD=∠ACB=25°,
又∵DE∥BC,
∴∠CDE=∠BCD=25°,
答:∠CDE的度数为25°.
17.∵∠DAB+∠D=180°,
∴CD∥AB,
∴∠DCE=∠B=95°,
∵∠CAD=25°,AC平分∠DAB,
∴∠CAB=∠CAD=25°,∠DAB=2∠CAD=50°,
∴∠D=180°-∠DAB=130°,
∴∠DCA=180°-∠D-∠CAD=25°.
18.证明:∵平分,
∴∠BAE=,
∵,
∴∠ADB=90°,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=,
∴.
19.(1)解:如图1,为边上的高.
(2)解:,
,
平分,
,
为边上的高,
,
,
,
.
20.(1)解:∵ ∠ABC=42°, ∠C=78°,
∴ ∠BAC=180°-∠ABC-∠C=60°.
∵ AD平分∠BAC,
∴ ∠BAD=∠BAC=30°.
∴ ∠ADC=∠ABC+∠BAD=42°+30°=72°.
(2)解:如图1所示,AE为BD边上的高,BF为AD边上的高.
在△ADE和△BFD中,
∵ ∠AED=∠BFD=90°,∠ADE=∠BDF,
∴ ∠DAE=∠DBF.
∴ ∠DAE=180°-∠AED-∠ADE =180°-90°-72°=18°.
(3)解:∠DAE=(∠C-∠ABC),
理由如下:∵∠ADE是△ABD的外角,
∴∠ADE=∠ABC+∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠BAC=(180°-∠ABC-∠C),
∴∠ADE=∠ABD+∠BAD=∠ABC+(180°-∠ABC-∠C)=90°+∠ABC-∠C,
∵AE⊥BC,
∴∠AED=90°,
∴∠DAE=90°-∠ADE=90°-(90°+∠ABC-∠C)=∠C-∠ABC=(∠C-∠ABC),
即∠DAE=(∠C-∠ABC).
21.(1)110°,
(2)∵,
∴,
∵、是角平分线,
∴,
∴,
(3)
由图可知
∵,
∴,
∴,
∴,
∴,
∴.
