【必考点解析】沪教版(上海)八下 第二十三章概率初步月考试卷(精选含答案)
文档属性
| 名称 | 【必考点解析】沪教版(上海)八下 第二十三章概率初步月考试卷(精选含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 17:13:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级数学第二学期第二十三章概率初步月考
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内 ( http: / / www.21cnjy.com )相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21·世纪*教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、在进行一个游戏时,游戏的次数和某种结果出现的频率如表所示,则该游戏是什么,其结果可能是什么?
下面分别是甲、乙两名同学的答案:
游戏次数 100 200 400 1000
频率 0.32 0.34 0.325 0.332
甲:掷一枚质地均匀的骰子,向上的点数与4相差1;
乙:在“石头、剪刀、布”的游戏中,琪琪随机出的是“剪刀”( )
A.甲正确,乙错误 B.甲错误,乙正确
C.甲、乙均正确 D.甲、乙均错误
2、不透明的布袋内装有形状、大小、质地完全相同的1个白球,2个红球,3个黑球,若随机摸出一个球恰是黑球的概率为( )【出处:21教育名师】
A. B. C. D.
3、下列事件为必然事件的是( )
A.打开电视,正在播放广告
B.抛掷一枚硬币,正面向上
C.挪一枚质地均匀的般子,向上一面的点数为7
D.实心铁块放入水中会下沉
4、下列事件中,属于不可能事件的是( )
A.射击运动员射击一次,命中靶心
B.从一个只装有白球和红球的袋中摸球,摸出黄球
C.班里的两名同学,他们的生日是同一天
D.经过红绿灯路口,遇到绿灯
5、下列事件中,是必然事件的是( )
A.如果a2=b2,那么a=b
B.车辆随机到达一个路口,遇到红灯
C.2021年有366天
D.13个人中至少有两个人生肖相同
6、某十字路口的交通信号灯,每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是绿灯的可能性大小为( )21·cn·jy·com
A. B. C. D.
7、下列说法正确的是( )
A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨
B.“抛一枚硬币正面朝上的概率为”表示每抛两次就有一次正面朝上
C.“彩票中奖的概率是1%”表示买100张彩票肯定会中奖
D.“抛一枚均匀的正方体骰子,朝上的点数是2的概率为”表示随着抛掷次数的增加,“拋出朝上的点数是2”这一事件发生的概率稳定在附近21教育名师原创作品
8、从分别标有号数1到10的10张除标号外完全一样的卡片中,随意抽取一张,其号数为3的倍数的概率是( )
A. B. C. D.
9、下列事件是必然事件的是( )
A.抛一枚硬币正面朝上
B.若a为实数,则a2≥0
C.某运动员射击一次击中靶心
D.明天一定是晴天
10、下列事件中,是必然事件的是( )
A.同位角相等
B.打开电视,正在播出特别节目《战疫情》
C.经过红绿灯路口,遇到绿灯
D.长度为4,6,9的三条线段可以围成一个三角形.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、在0,1,2,3,4,5这六个数中,随机取出一个数记为a,使得关于x的一元二次方程有实数解的概率是______.
2、四张背面相同的扑克牌,分别为红桃1,2,3,4,背面朝上,先从中抽取一张把抽到的点数记为a,再在剩余的扑克中抽取一张点数记为b,则以为坐标的点在直线上的概率为______.
3、在一个不透明的布袋中 ( http: / / www.21cnjy.com ),黄色、红色的乒乓球共10个,这些球除颜色外其他都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中红色球的个数很可能是___个.
4、粉笔盒中有10支白色粉笔盒若干支彩色粉笔,每支粉笔除颜色外均相同,从中随机拿一支粉笔,拿到白色的概率为,则其中彩色粉笔的数量为________支.
5、在不透明的袋中装有仅颜色不同的一个红球和 ( http: / / www.21cnjy.com )一个蓝球,从此袋中随机摸出一个小球,然后放回,再随机摸出一个小球,则两次摸出的球颜色不同的概率是______
三、解答题(5小题,每小题10分,共计50分)
1、一个不透明的口袋中有四个分别标号为1,2,3,4的完全相同的小球,从中随机摸取两个小球.
(1)请列举出所有可能结果;
(2)求取出的两个小球标号和等于5的概率.
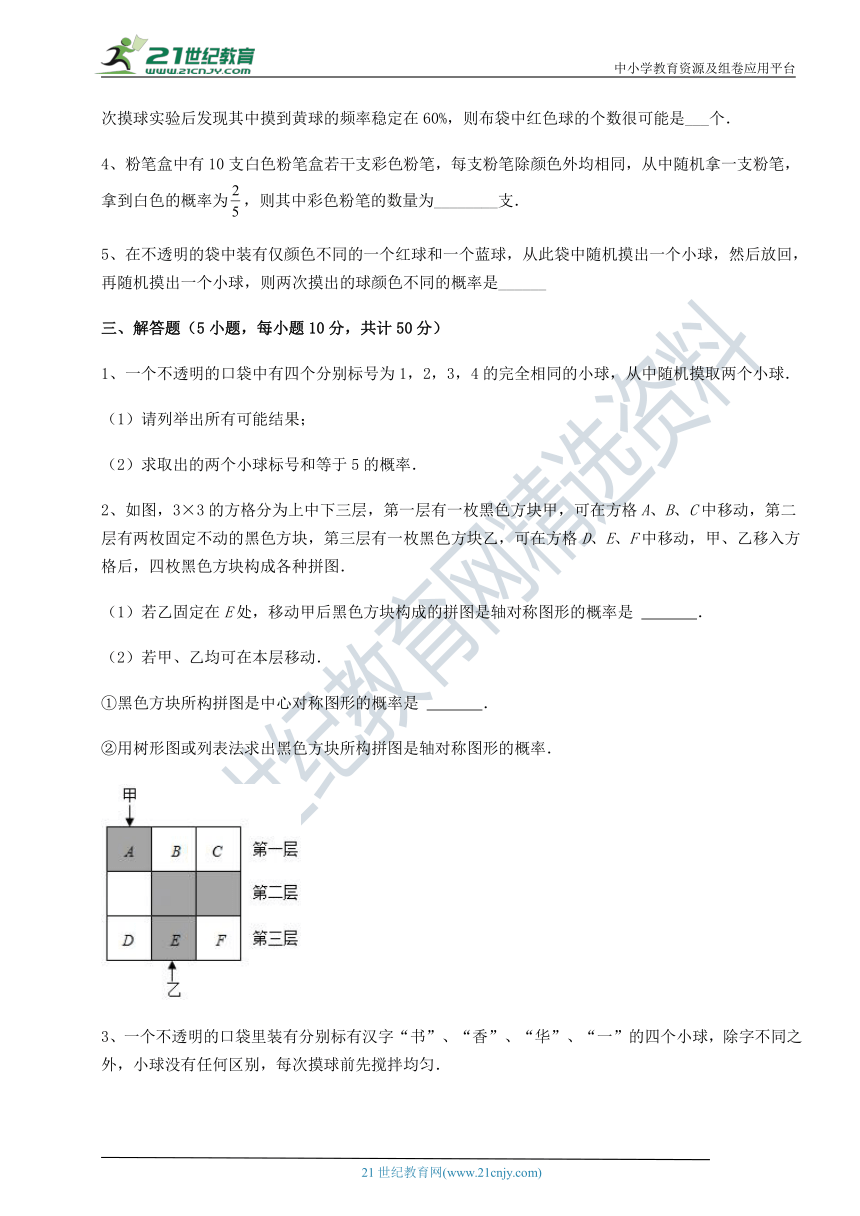
2、如图,3×3的方格分为上中 ( http: / / www.21cnjy.com )下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.21cnjy.com
(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是 .
(2)若甲、乙均可在本层移动.
①黑色方块所构拼图是中心对称图形的概率是 .
②用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
( http: / / www.21cnjy.com / )
3、一个不透明的口袋里装有分别标有汉字“书”、“香”、“华”、“一”的四个小球,除字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是“书”的概率为 ;
(2)从中随机取出两球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“华一”的概率.
4、某校开展“经典诵读” ( http: / / www.21cnjy.com )比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A、B、C依次表示这三个诵读材料),将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小华和小敏参加诵读比赛,比赛时小华先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小敏从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小华诵读《弟子规》的概率是 .
(2)请用列表法或画树状图法求小华和小敏诵读两个不同材料的概率.
5、有4个完全相同的小球,把它们分别标号为1、2、3、4,放在一个口袋中,随机的摸出一个小球然后放回,再随机的摸出一个小球.
(1)求两次摸出的球的标号相同的概率;
(2)求两次摸出的球的标号的和等于4的概率.
-参考答案-
一、单选题
1、C
【分析】
由表可知该种结果出现的概率约为,对甲乙两人所描述的游戏进行判断即可.
【详解】
由表可知该种结果出现的概率约为
∵掷一枚质地均匀的骰子,向上的点数有1、2、3、4、5、6
∴向上的点数与4相差1有3、5
∴掷一枚质地均匀的骰子,向上的点数与4相差1的概率为
∴甲的答案正确
又∵“石头、剪刀、布”的游戏中,琪琪随机出的是“剪刀”概率为
∴乙的答案正确
综上所述甲、乙答案均正确.
故选C.
【点睛】
本题考查了用频率估计概率,其做法是取多次试验发生的频率稳定值来估计概率.
2、B
【分析】
由在不透明的布袋中装有1个白球,2个红球,3个黑球,利用概率公式直接求解即可求得答案.
【详解】
解:∵在不透明的布袋中装有1个白球,2个红球,3个黑球,
∴从袋中任意摸出一个球,摸出的球是红球的概率是:.
故选:B.
【点睛】
此题考查了概率公式的应用.注意概率=所求情况数与总情况数之比.
3、D
【分析】
根据必然事件的定义:在一定条件下,一定会发生的事件,进行逐一判断即可.
【详解】
解:A、打开电视,可以正在播放广告,也可以不在播放广告,不是必然事件,不符合题意;
B、抛掷一枚硬币,正面可以向上,反面也可以向上,不是必然事件,不符合题意;
C、挪一枚质地均匀的般子,向上一面的点数为7,这是不可能发生的,不是必然事件,不符合题意;
D、实心铁块放入水中会下沉,这是一定会发生的,是必然事件,符合题意;
故选D.
【点睛】
本题主要考查必然事件,熟知必然事件的定义是解题的关键.
4、B
【分析】
根据不可能事件的意义,结合具体的问题情境进行判断即可.
【详解】
解:A、射击运动员射击一次,命中靶心,是随机事件;故A不符合题意;
B、从一个只装有白球和红球的袋中摸球,摸出黄球,是不可能事件,故B符合题意;
C、班里的两名同学,他们的生日是同一天,是随机事件;故C不符合题意;
D、经过红绿灯路口,遇到绿灯,是随机事件,故D不符合题意;
故选:B.
【点睛】
本题考查随机事件,不可能事件,必然事件,理解随机事件,不可能事件,必然事件的意义是正确判断的前提.
5、D
【分析】
在一定的条件下重复进行试验时,有的事件在每次试验中必然会发生,这样的事件叫必然发生的事件,简称必然事件;利用概念逐一分析即可得到答案.2-1-c-n-j-y
【详解】
解:如果a2=b2,那么,原说法是随机事件,故A不符合题意;
车辆随机到达一个路口,遇到红灯,是随机事件,故B不符合题意;
2021年是平年,有365天,原说法是不可能事件,故C不符合题意;
13个人中至少有两个人生肖相同,是必然事件,故D符合题意,
故选:D.
【点睛】
本题考查的是必然事件的概念,不可能事件,随机事件的含义,掌握“必然事件的概念”是解本题的关键.
6、C
【分析】
用绿灯亮的时间除以三种灯亮总时间即可解答.
【详解】
解:除以三种灯亮总时间是30+25+5=60秒,绿灯亮25秒,
所以绿灯的概率是:.
故选C.
【点睛】
本题主要考查了概率的基本计算,掌握概率等于所求情况数与总情况数之比是解答本题的关键.
7、D
【分析】
根据概率的意义去判断即可.
【详解】
∵“明天降雨的概率是80%”表示明天有降雨的可能性是80%,
∴A说法错误;
∵抛一枚硬币正面朝上的概率为”表示正面向上的可能性是,
∴B说法错误;
∵“彩票中奖的概率是1%”表示中奖的可能性是1%,
∴C说法错误;
∵“抛一枚均匀的正方体骰子,朝上的点数是2的概率为”表示随着抛掷次数的增加,“拋出朝上的点数是2”这一事件发生的概率稳定在附近,www.21-cn-jy.com
∴D说法正确;
故选D.
【点睛】
本题考查了概率的意义,正确理解概率的意义是解题的关键.
8、C
【分析】
用3的倍数的个数除以数的总数即为所求的概率.
【详解】
解:∵1到10的数字中是3的倍数的有3,6,9共3个,
∴卡片上的数字是3的倍数的概率是.
故选:C.
【点睛】
本题考查概率的求法.用到的知识点为:概率=所求情况数与总情况数之比.
9、B
【分析】
根据必然事件的定义对选项逐个判断即可.
【详解】
解:A、抛一枚硬币正面朝上,是随机事件,不符合题意;
B、若a为实数,则a2≥0,是必然事件,符合题意;
C、某运动员射击一次击中靶心,是随机事件,不符合题意;
D、明天一定是晴天,是随机事件,不符合题意,
故选:B
【点睛】
本题主要考查了必然事件的定义,熟练掌握必 ( http: / / www.21cnjy.com )然事件,在一定的条件下重复进行试验时,有的事件在每次试验中必然会发生,这样的事件叫必然发生的事件,简称必然事件是解题的关键.
10、D
【分析】
根据必然事件的概念即可得出答案.
【详解】
解:∵同位角不一定相等,为随机事件,
∴A选项不合题意,
∵打开电视,不一定正在播出特别节目《战疫情》,为随机事件,
∴B选项不合题意,
∵车辆随机到达一个路口,可能遇到红灯,也可能遇到绿灯,为随机事件,
∴C选项不合题意,
∵4+6>9,
∴长度为4,6,9的三条线段可以围成一个三角形为必然事件,.
∴D选项符合题意,
故选:D.
【点睛】
本题主要考查必然事件的概念,必然事件是指一定会发生的事件,关键是要牢记必然事件的概念.
二、填空题
1、
【分析】
根据题意,分,时,进而求得一元二次方程根的判别式不小于0的情形数量,即可求得概率.
【详解】
解:当时,该方程不是一元二次方程,
当时,
解得
时,关于x的一元二次方程有实数解
随机取出一个数记为a,使得关于x的一元二次方程有实数解的概率是
故答案为:
【点睛】
本题考查了利用概率公式计算概率,一元二次方程根的判别式判断根的情况,一元二次方程的定义,掌握以上知识是解题的关键.当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程没有实数根.21教育网
2、
【分析】
首先画出树状图即可求得所有等可能的结果与点(a,b)在直线上的情况,然后利用概率公式求解即可求得答案.【版权所有:21教育】
【详解】
解:画树状图得:
( http: / / www.21cnjy.com / )
由树形图可知:一共有12种等可能的结果,其中点(a,b)在直线上的有3种结果,
所以点(a,b)在直线上的概率为,
故答案为:.
【点睛】
本题考查的是用列表法或画 ( http: / / www.21cnjy.com )树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.21*cnjy*com
3、4
【分析】
设出黄球的个数,根据黄球的频率求出黄球的个数即可解答.
【详解】
设黄球的个数为x,
∵共有黄色、红色的乒乓球10个,黄球的频率稳定在60%,
∴,
解得:,
∴布袋中红色球的个数很可能是(个).
故答案为:4.
【点睛】
本题考查了利用频率估计概率,大量反复试验下频率稳定值即概率,关键是根据黄球的频率得到相应的等量关系,列出方程.www-2-1-cnjy-com
4、15
【分析】
设彩色笔的数量为x支,然后根据概率公式列出方程求解即可.
【详解】
解:设彩色笔的数量为x支,
由题意得:,
解得,
经检验是原方程的解,
∴彩色笔为15支,
故答案为:15.
【点睛】
本题主要考查了概率公式和分式方程,解题的关键在于能够熟练掌握概率公式列出方程进行求解.
5、
【分析】
根据题意,列表分析所有可能,然后运用概率公式求解即可.
【详解】
解:列表如下,表示红球,表示蓝球
第一次\第二次
总共4种情况,两次摸出的球颜色不同的2种.
所以两次摸出的球颜色不同的概率是
故答案是:.
【点睛】
本题考查了列表法求概率,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果数,概率=所求情况数与总情况数之比.2·1·c·n·j·y
三、解答题
1、(1)见详解;(2).
【分析】
(1)根据题意通过列出相应的表格,即可得出所有可能结果;
(2)由题意利用取出的两个小球标号和等于5的结果数除以所有可能结果数即可得出答案.
【详解】
解:(1)由题意列表得:
1 2 3 4
1 --- (2,1) (3,1) (4,1)
2 (1,2) --- (3,2) (4,2)
3 (1,3) (2,3) --- (4,3)
4 (1,4) (2,4) (3,4) ---
所有可能的结果有12种;
(2)由(1)表格可知取出的两个小球标号和等于5的结果有(1,4)、(2,3)、(3,2)、(4,1)共4种,而所有可能的结果有12种,21世纪教育网版权所有
所以取出的两个小球标号和等于5的概率.
【点睛】
本题考查的是用列表法或树 ( http: / / www.21cnjy.com )状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.【来源:21·世纪·教育·网】
2、(1);(2)①;②.
【分析】
(1)直接由概率公式求解即可;
(2)①黑色方块所构拼图中是中心对称图形有两种情形,由概率公式求解即可;
②画树状图,再由概率公式求解即可.
【详解】
解:(1)若乙固定在E处,黑色方块甲,可在方格A、B、C中移动,且当在A、B处时,黑色方块构成的拼图是轴对称图形【来源:21cnj*y.co*m】
所以移动甲后黑色方块构成的拼图是轴对称图形的概率是;
(2)①甲、乙在本层移动,一共有 种情况,其中黑色方块所构拼图中是中心对称图形有两种情形:a、甲在B处,乙在F处;b、甲在C处,乙在E处,
所以黑色方块所构拼图是中心对称图形的概率是;
②画树状图如图:
( http: / / www.21cnjy.com / )
由树状图可知,共有9个等可能的结果,黑色方块所构拼图是轴对称图形的结果有5个,
∴黑色方块所构拼图是轴对称图形的概率=.
【点睛】
本题考查了列表法与树状图法、轴对称图形、中心对称图形等知识;熟练掌握轴对称图形、中心对称图形,正确画出树状图是解题的关键.
3、(1);(2)
【分析】
(1)根据概率公式计算即可;
(2)画出树状图计算即可;
【详解】
(1)由题可得,球上的汉字刚好是“书”的概率为;
故答案是:;
(2)根据题意画出树状图如下:
( http: / / www.21cnjy.com / )
则取出的两个球上的汉字能组成“华一”的概率为.
【点睛】
本题主要考查了概率公式和树状图法求概率,准确画图计算是解题的关键.
4、(1);(2)
【分析】
(1)直接根据概率公式求解;
(2)利用列表法展示所有9种等可能性结果,再找出小华和小敏诵读两个不同材料的结果数,然后根据概率公式求解.21*cnjy*com
【详解】
解:(1)小华诵读《弟子规》的概率=;
故答案为:;
(2)列表得:
小华小敏 A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格可知,共有9种等可能性结果,其中小华和小敏诵读两个不同材料的结果有6种,
∴P(小华和小敏诵读两个不同材料)=
【点睛】
本题考查了列表法与树状图法: ( http: / / www.21cnjy.com )利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.
5、(1);(2)
【分析】
(1)先列出树状图,找到所有的等可能性的结果数,然后找到两次摸出的球的标号相同的结果数,最后利用概率公式求解即可;
(2)根据(1)所列树状图,找到两次摸出的球的标号和为4的结果数,利用概率公式求解即可.
【详解】
解:(1)列树状图如下所示:
( http: / / www.21cnjy.com / )
由树状图可知一共有16种等可能性的结果数,其中两次摸出的球的标号相同的结果数有4种,
∴(两次摸出的球的标号相同);
(2)由树状图可知一共有16种等可能性的结果数,其中两次摸出的球的标号的和为4的结果数有(1,3),(2,2),(3,1)3种,
∴(两次摸出的球的标号的和等于4).
【点睛】
本题主要考查了树状图法或列表法求解概率,解题的关键在于能够熟练掌握树状图法或列表法求解概率.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学第二学期第二十三章概率初步月考
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内 ( http: / / www.21cnjy.com )相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21·世纪*教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、在进行一个游戏时,游戏的次数和某种结果出现的频率如表所示,则该游戏是什么,其结果可能是什么?
下面分别是甲、乙两名同学的答案:
游戏次数 100 200 400 1000
频率 0.32 0.34 0.325 0.332
甲:掷一枚质地均匀的骰子,向上的点数与4相差1;
乙:在“石头、剪刀、布”的游戏中,琪琪随机出的是“剪刀”( )
A.甲正确,乙错误 B.甲错误,乙正确
C.甲、乙均正确 D.甲、乙均错误
2、不透明的布袋内装有形状、大小、质地完全相同的1个白球,2个红球,3个黑球,若随机摸出一个球恰是黑球的概率为( )【出处:21教育名师】
A. B. C. D.
3、下列事件为必然事件的是( )
A.打开电视,正在播放广告
B.抛掷一枚硬币,正面向上
C.挪一枚质地均匀的般子,向上一面的点数为7
D.实心铁块放入水中会下沉
4、下列事件中,属于不可能事件的是( )
A.射击运动员射击一次,命中靶心
B.从一个只装有白球和红球的袋中摸球,摸出黄球
C.班里的两名同学,他们的生日是同一天
D.经过红绿灯路口,遇到绿灯
5、下列事件中,是必然事件的是( )
A.如果a2=b2,那么a=b
B.车辆随机到达一个路口,遇到红灯
C.2021年有366天
D.13个人中至少有两个人生肖相同
6、某十字路口的交通信号灯,每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是绿灯的可能性大小为( )21·cn·jy·com
A. B. C. D.
7、下列说法正确的是( )
A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨
B.“抛一枚硬币正面朝上的概率为”表示每抛两次就有一次正面朝上
C.“彩票中奖的概率是1%”表示买100张彩票肯定会中奖
D.“抛一枚均匀的正方体骰子,朝上的点数是2的概率为”表示随着抛掷次数的增加,“拋出朝上的点数是2”这一事件发生的概率稳定在附近21教育名师原创作品
8、从分别标有号数1到10的10张除标号外完全一样的卡片中,随意抽取一张,其号数为3的倍数的概率是( )
A. B. C. D.
9、下列事件是必然事件的是( )
A.抛一枚硬币正面朝上
B.若a为实数,则a2≥0
C.某运动员射击一次击中靶心
D.明天一定是晴天
10、下列事件中,是必然事件的是( )
A.同位角相等
B.打开电视,正在播出特别节目《战疫情》
C.经过红绿灯路口,遇到绿灯
D.长度为4,6,9的三条线段可以围成一个三角形.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、在0,1,2,3,4,5这六个数中,随机取出一个数记为a,使得关于x的一元二次方程有实数解的概率是______.
2、四张背面相同的扑克牌,分别为红桃1,2,3,4,背面朝上,先从中抽取一张把抽到的点数记为a,再在剩余的扑克中抽取一张点数记为b,则以为坐标的点在直线上的概率为______.
3、在一个不透明的布袋中 ( http: / / www.21cnjy.com ),黄色、红色的乒乓球共10个,这些球除颜色外其他都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中红色球的个数很可能是___个.
4、粉笔盒中有10支白色粉笔盒若干支彩色粉笔,每支粉笔除颜色外均相同,从中随机拿一支粉笔,拿到白色的概率为,则其中彩色粉笔的数量为________支.
5、在不透明的袋中装有仅颜色不同的一个红球和 ( http: / / www.21cnjy.com )一个蓝球,从此袋中随机摸出一个小球,然后放回,再随机摸出一个小球,则两次摸出的球颜色不同的概率是______
三、解答题(5小题,每小题10分,共计50分)
1、一个不透明的口袋中有四个分别标号为1,2,3,4的完全相同的小球,从中随机摸取两个小球.
(1)请列举出所有可能结果;
(2)求取出的两个小球标号和等于5的概率.
2、如图,3×3的方格分为上中 ( http: / / www.21cnjy.com )下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.21cnjy.com
(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是 .
(2)若甲、乙均可在本层移动.
①黑色方块所构拼图是中心对称图形的概率是 .
②用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
( http: / / www.21cnjy.com / )
3、一个不透明的口袋里装有分别标有汉字“书”、“香”、“华”、“一”的四个小球,除字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是“书”的概率为 ;
(2)从中随机取出两球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“华一”的概率.
4、某校开展“经典诵读” ( http: / / www.21cnjy.com )比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A、B、C依次表示这三个诵读材料),将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小华和小敏参加诵读比赛,比赛时小华先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小敏从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小华诵读《弟子规》的概率是 .
(2)请用列表法或画树状图法求小华和小敏诵读两个不同材料的概率.
5、有4个完全相同的小球,把它们分别标号为1、2、3、4,放在一个口袋中,随机的摸出一个小球然后放回,再随机的摸出一个小球.
(1)求两次摸出的球的标号相同的概率;
(2)求两次摸出的球的标号的和等于4的概率.
-参考答案-
一、单选题
1、C
【分析】
由表可知该种结果出现的概率约为,对甲乙两人所描述的游戏进行判断即可.
【详解】
由表可知该种结果出现的概率约为
∵掷一枚质地均匀的骰子,向上的点数有1、2、3、4、5、6
∴向上的点数与4相差1有3、5
∴掷一枚质地均匀的骰子,向上的点数与4相差1的概率为
∴甲的答案正确
又∵“石头、剪刀、布”的游戏中,琪琪随机出的是“剪刀”概率为
∴乙的答案正确
综上所述甲、乙答案均正确.
故选C.
【点睛】
本题考查了用频率估计概率,其做法是取多次试验发生的频率稳定值来估计概率.
2、B
【分析】
由在不透明的布袋中装有1个白球,2个红球,3个黑球,利用概率公式直接求解即可求得答案.
【详解】
解:∵在不透明的布袋中装有1个白球,2个红球,3个黑球,
∴从袋中任意摸出一个球,摸出的球是红球的概率是:.
故选:B.
【点睛】
此题考查了概率公式的应用.注意概率=所求情况数与总情况数之比.
3、D
【分析】
根据必然事件的定义:在一定条件下,一定会发生的事件,进行逐一判断即可.
【详解】
解:A、打开电视,可以正在播放广告,也可以不在播放广告,不是必然事件,不符合题意;
B、抛掷一枚硬币,正面可以向上,反面也可以向上,不是必然事件,不符合题意;
C、挪一枚质地均匀的般子,向上一面的点数为7,这是不可能发生的,不是必然事件,不符合题意;
D、实心铁块放入水中会下沉,这是一定会发生的,是必然事件,符合题意;
故选D.
【点睛】
本题主要考查必然事件,熟知必然事件的定义是解题的关键.
4、B
【分析】
根据不可能事件的意义,结合具体的问题情境进行判断即可.
【详解】
解:A、射击运动员射击一次,命中靶心,是随机事件;故A不符合题意;
B、从一个只装有白球和红球的袋中摸球,摸出黄球,是不可能事件,故B符合题意;
C、班里的两名同学,他们的生日是同一天,是随机事件;故C不符合题意;
D、经过红绿灯路口,遇到绿灯,是随机事件,故D不符合题意;
故选:B.
【点睛】
本题考查随机事件,不可能事件,必然事件,理解随机事件,不可能事件,必然事件的意义是正确判断的前提.
5、D
【分析】
在一定的条件下重复进行试验时,有的事件在每次试验中必然会发生,这样的事件叫必然发生的事件,简称必然事件;利用概念逐一分析即可得到答案.2-1-c-n-j-y
【详解】
解:如果a2=b2,那么,原说法是随机事件,故A不符合题意;
车辆随机到达一个路口,遇到红灯,是随机事件,故B不符合题意;
2021年是平年,有365天,原说法是不可能事件,故C不符合题意;
13个人中至少有两个人生肖相同,是必然事件,故D符合题意,
故选:D.
【点睛】
本题考查的是必然事件的概念,不可能事件,随机事件的含义,掌握“必然事件的概念”是解本题的关键.
6、C
【分析】
用绿灯亮的时间除以三种灯亮总时间即可解答.
【详解】
解:除以三种灯亮总时间是30+25+5=60秒,绿灯亮25秒,
所以绿灯的概率是:.
故选C.
【点睛】
本题主要考查了概率的基本计算,掌握概率等于所求情况数与总情况数之比是解答本题的关键.
7、D
【分析】
根据概率的意义去判断即可.
【详解】
∵“明天降雨的概率是80%”表示明天有降雨的可能性是80%,
∴A说法错误;
∵抛一枚硬币正面朝上的概率为”表示正面向上的可能性是,
∴B说法错误;
∵“彩票中奖的概率是1%”表示中奖的可能性是1%,
∴C说法错误;
∵“抛一枚均匀的正方体骰子,朝上的点数是2的概率为”表示随着抛掷次数的增加,“拋出朝上的点数是2”这一事件发生的概率稳定在附近,www.21-cn-jy.com
∴D说法正确;
故选D.
【点睛】
本题考查了概率的意义,正确理解概率的意义是解题的关键.
8、C
【分析】
用3的倍数的个数除以数的总数即为所求的概率.
【详解】
解:∵1到10的数字中是3的倍数的有3,6,9共3个,
∴卡片上的数字是3的倍数的概率是.
故选:C.
【点睛】
本题考查概率的求法.用到的知识点为:概率=所求情况数与总情况数之比.
9、B
【分析】
根据必然事件的定义对选项逐个判断即可.
【详解】
解:A、抛一枚硬币正面朝上,是随机事件,不符合题意;
B、若a为实数,则a2≥0,是必然事件,符合题意;
C、某运动员射击一次击中靶心,是随机事件,不符合题意;
D、明天一定是晴天,是随机事件,不符合题意,
故选:B
【点睛】
本题主要考查了必然事件的定义,熟练掌握必 ( http: / / www.21cnjy.com )然事件,在一定的条件下重复进行试验时,有的事件在每次试验中必然会发生,这样的事件叫必然发生的事件,简称必然事件是解题的关键.
10、D
【分析】
根据必然事件的概念即可得出答案.
【详解】
解:∵同位角不一定相等,为随机事件,
∴A选项不合题意,
∵打开电视,不一定正在播出特别节目《战疫情》,为随机事件,
∴B选项不合题意,
∵车辆随机到达一个路口,可能遇到红灯,也可能遇到绿灯,为随机事件,
∴C选项不合题意,
∵4+6>9,
∴长度为4,6,9的三条线段可以围成一个三角形为必然事件,.
∴D选项符合题意,
故选:D.
【点睛】
本题主要考查必然事件的概念,必然事件是指一定会发生的事件,关键是要牢记必然事件的概念.
二、填空题
1、
【分析】
根据题意,分,时,进而求得一元二次方程根的判别式不小于0的情形数量,即可求得概率.
【详解】
解:当时,该方程不是一元二次方程,
当时,
解得
时,关于x的一元二次方程有实数解
随机取出一个数记为a,使得关于x的一元二次方程有实数解的概率是
故答案为:
【点睛】
本题考查了利用概率公式计算概率,一元二次方程根的判别式判断根的情况,一元二次方程的定义,掌握以上知识是解题的关键.当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程没有实数根.21教育网
2、
【分析】
首先画出树状图即可求得所有等可能的结果与点(a,b)在直线上的情况,然后利用概率公式求解即可求得答案.【版权所有:21教育】
【详解】
解:画树状图得:
( http: / / www.21cnjy.com / )
由树形图可知:一共有12种等可能的结果,其中点(a,b)在直线上的有3种结果,
所以点(a,b)在直线上的概率为,
故答案为:.
【点睛】
本题考查的是用列表法或画 ( http: / / www.21cnjy.com )树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.21*cnjy*com
3、4
【分析】
设出黄球的个数,根据黄球的频率求出黄球的个数即可解答.
【详解】
设黄球的个数为x,
∵共有黄色、红色的乒乓球10个,黄球的频率稳定在60%,
∴,
解得:,
∴布袋中红色球的个数很可能是(个).
故答案为:4.
【点睛】
本题考查了利用频率估计概率,大量反复试验下频率稳定值即概率,关键是根据黄球的频率得到相应的等量关系,列出方程.www-2-1-cnjy-com
4、15
【分析】
设彩色笔的数量为x支,然后根据概率公式列出方程求解即可.
【详解】
解:设彩色笔的数量为x支,
由题意得:,
解得,
经检验是原方程的解,
∴彩色笔为15支,
故答案为:15.
【点睛】
本题主要考查了概率公式和分式方程,解题的关键在于能够熟练掌握概率公式列出方程进行求解.
5、
【分析】
根据题意,列表分析所有可能,然后运用概率公式求解即可.
【详解】
解:列表如下,表示红球,表示蓝球
第一次\第二次
总共4种情况,两次摸出的球颜色不同的2种.
所以两次摸出的球颜色不同的概率是
故答案是:.
【点睛】
本题考查了列表法求概率,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果数,概率=所求情况数与总情况数之比.2·1·c·n·j·y
三、解答题
1、(1)见详解;(2).
【分析】
(1)根据题意通过列出相应的表格,即可得出所有可能结果;
(2)由题意利用取出的两个小球标号和等于5的结果数除以所有可能结果数即可得出答案.
【详解】
解:(1)由题意列表得:
1 2 3 4
1 --- (2,1) (3,1) (4,1)
2 (1,2) --- (3,2) (4,2)
3 (1,3) (2,3) --- (4,3)
4 (1,4) (2,4) (3,4) ---
所有可能的结果有12种;
(2)由(1)表格可知取出的两个小球标号和等于5的结果有(1,4)、(2,3)、(3,2)、(4,1)共4种,而所有可能的结果有12种,21世纪教育网版权所有
所以取出的两个小球标号和等于5的概率.
【点睛】
本题考查的是用列表法或树 ( http: / / www.21cnjy.com )状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.【来源:21·世纪·教育·网】
2、(1);(2)①;②.
【分析】
(1)直接由概率公式求解即可;
(2)①黑色方块所构拼图中是中心对称图形有两种情形,由概率公式求解即可;
②画树状图,再由概率公式求解即可.
【详解】
解:(1)若乙固定在E处,黑色方块甲,可在方格A、B、C中移动,且当在A、B处时,黑色方块构成的拼图是轴对称图形【来源:21cnj*y.co*m】
所以移动甲后黑色方块构成的拼图是轴对称图形的概率是;
(2)①甲、乙在本层移动,一共有 种情况,其中黑色方块所构拼图中是中心对称图形有两种情形:a、甲在B处,乙在F处;b、甲在C处,乙在E处,
所以黑色方块所构拼图是中心对称图形的概率是;
②画树状图如图:
( http: / / www.21cnjy.com / )
由树状图可知,共有9个等可能的结果,黑色方块所构拼图是轴对称图形的结果有5个,
∴黑色方块所构拼图是轴对称图形的概率=.
【点睛】
本题考查了列表法与树状图法、轴对称图形、中心对称图形等知识;熟练掌握轴对称图形、中心对称图形,正确画出树状图是解题的关键.
3、(1);(2)
【分析】
(1)根据概率公式计算即可;
(2)画出树状图计算即可;
【详解】
(1)由题可得,球上的汉字刚好是“书”的概率为;
故答案是:;
(2)根据题意画出树状图如下:
( http: / / www.21cnjy.com / )
则取出的两个球上的汉字能组成“华一”的概率为.
【点睛】
本题主要考查了概率公式和树状图法求概率,准确画图计算是解题的关键.
4、(1);(2)
【分析】
(1)直接根据概率公式求解;
(2)利用列表法展示所有9种等可能性结果,再找出小华和小敏诵读两个不同材料的结果数,然后根据概率公式求解.21*cnjy*com
【详解】
解:(1)小华诵读《弟子规》的概率=;
故答案为:;
(2)列表得:
小华小敏 A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格可知,共有9种等可能性结果,其中小华和小敏诵读两个不同材料的结果有6种,
∴P(小华和小敏诵读两个不同材料)=
【点睛】
本题考查了列表法与树状图法: ( http: / / www.21cnjy.com )利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.
5、(1);(2)
【分析】
(1)先列出树状图,找到所有的等可能性的结果数,然后找到两次摸出的球的标号相同的结果数,最后利用概率公式求解即可;
(2)根据(1)所列树状图,找到两次摸出的球的标号和为4的结果数,利用概率公式求解即可.
【详解】
解:(1)列树状图如下所示:
( http: / / www.21cnjy.com / )
由树状图可知一共有16种等可能性的结果数,其中两次摸出的球的标号相同的结果数有4种,
∴(两次摸出的球的标号相同);
(2)由树状图可知一共有16种等可能性的结果数,其中两次摸出的球的标号的和为4的结果数有(1,3),(2,2),(3,1)3种,
∴(两次摸出的球的标号的和等于4).
【点睛】
本题主要考查了树状图法或列表法求解概率,解题的关键在于能够熟练掌握树状图法或列表法求解概率.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
