【必考点解析】沪教版(上海)八下 第二十三章概率初步章节测评试题(精选,含解析)
文档属性
| 名称 | 【必考点解析】沪教版(上海)八下 第二十三章概率初步章节测评试题(精选,含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级数学第二学期第二十三章概率初步章节测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指 ( http: / / www.21cnjy.com )定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【来源:21cnj*y.co*m】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、甲、乙两位同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A.掷一枚正六面体的骰子,出现1点的概率
B.一个袋子中有2个白球和1个红球,从中任取一个球,则取到红球的概率
C.抛一枚硬币,出现正面的概率
D.任意写一个整数,它能被2整除的概率
2、同时抛两枚质地均匀的正方体骰子,骰子的六个面上分别刻有的点数,则下列事件中是必然事件的是( )21教育名师原创作品
A.点数之和为奇数 B.点数之和为偶数 C.点数之和大于 D.点数之和小于
3、 “2022年春节期间,中山市会下雨”这一事件为( )
A.必然事件 B.不可能事件 C.确定事件 D.随机事件
4、一个不透明的袋子中装 ( http: / / www.21cnjy.com )有四个小球,它们除了分别标有的数字1,2,3,6不同外,其他完全相同,任意从袋子中摸出一球后不放回,再任意摸出一球,则两次摸出的球所标数字之积为6的概率是( )
A. B. C. D.
5、一个口袋中有红色、黄色、蓝色玻璃球共200个,小明通过大量摸球试验后,发现摸到红球的频率为35%,则估计红球的个数约为( )
A.35个 B.60个 C.70个 D.130个
6、下列事件中,是随机事件的为( )
A.通常加热到100℃时,水沸腾
B.任意画一个三角形,其内角和是360°
C.三角形中,任意两边之和大于第三边
D.随意翻到一本书的某页,这页的页码是奇数
7、如图,一只小狗在如图所示的方砖上走来走去,最终停留在阴影方砖上的概率是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8、假如每个鸟卵都可以成功孵化小鸟,且孵化出 ( http: / / www.21cnjy.com )的小鸟是雄性和雌性的可能性相等.现有2枚鸟卵,孵化出的小鸟恰有一个雌性一个雄性的概率是( )2·1·c·n·j·y
A. B. C. D.
9、关于“明天是晴天的概率为90%”,下列说法正确的是( ).
A.明天一定是晴天 B.明天一定不是晴天
C.明天90%的地方是晴天 D.明天是晴天的可能性很大
10、在一个不透明的布袋中,红色、 ( http: / / www.21cnjy.com )黑色、白色的玻璃球共有60个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在0.15和0.45,则布袋中白色球的个数可能是( )
A.24 B.18 C.16 D.6
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、一个袋中有形状材料均相同的白球2个、红球3个,任意摸一个球是红球的概率_____.
2、四张背面相同的扑克牌,分别为红桃1,2,3,4,背面朝上,先从中抽取一张把抽到的点数记为a,再在剩余的扑克中抽取一张点数记为b,则以为坐标的点在直线上的概率为______.
3、综艺节目《朗读者》自开播以来受到大家 ( http: / / www.21cnjy.com )的广泛关注.重庆实验外国语学校某班主任准备从经常关注该节目的同学中抽取两人进行交流讨论,其中经常关注的同学中有3名男同学,1名女同学,则恰好抽取到1名男同学和1名女同学的概率是_________.
4、小张、小王和小李三人相 ( http: / / www.21cnjy.com )约去参加“抗疫情党员志愿者进社区服务”活动,现在有A、B、C三个社区可供随机选择,他们三人恰好进入同一社区的概率是____________.
5、在一个不透明的袋子中,装有若干个除颜色外都相同的小球,其中有8个红球和n个黑球,从袋中任意摸出一个球,若摸出黑球的概率是,则n=_____.
三、解答题(5小题,每小题10分,共计50分)
1、一个不透明的口袋中有四个分别标号为1,2,3,4的完全相同的小球,从中随机摸取两个小球.
(1)请列举出所有可能结果;
(2)求取出的两个小球标号和等于5的概率.
2、有4个完全相同的小球,把它们分别标号为1、2、3、4,放在一个口袋中,随机的摸出一个小球然后放回,再随机的摸出一个小球.www.21-cn-jy.com
(1)求两次摸出的球的标号相同的概率;
(2)求两次摸出的球的标号的和等于4的概率.
3、今年夏天,某市出现大暴雨,部分街区 ( http: / / www.21cnjy.com )积水严重,小明和小亮所在的社区为了做好排涝工作,特招募社区抗涝志愿工作者.小明和小亮决定报名参加,根据规定,志愿者会被随机分到A(淤泥清理),B(垃圾搬运),C(街道冲洗),D(消毒灭杀)其中一组.
(1)志愿者小明被分配到D组服务是 .
A.不可能事件;B.随机事件;C.必然事件;D.确定事件.
(2)请用列表或画树状图的方法,求出志愿者小明和小亮被分配到同一组服务的概率.
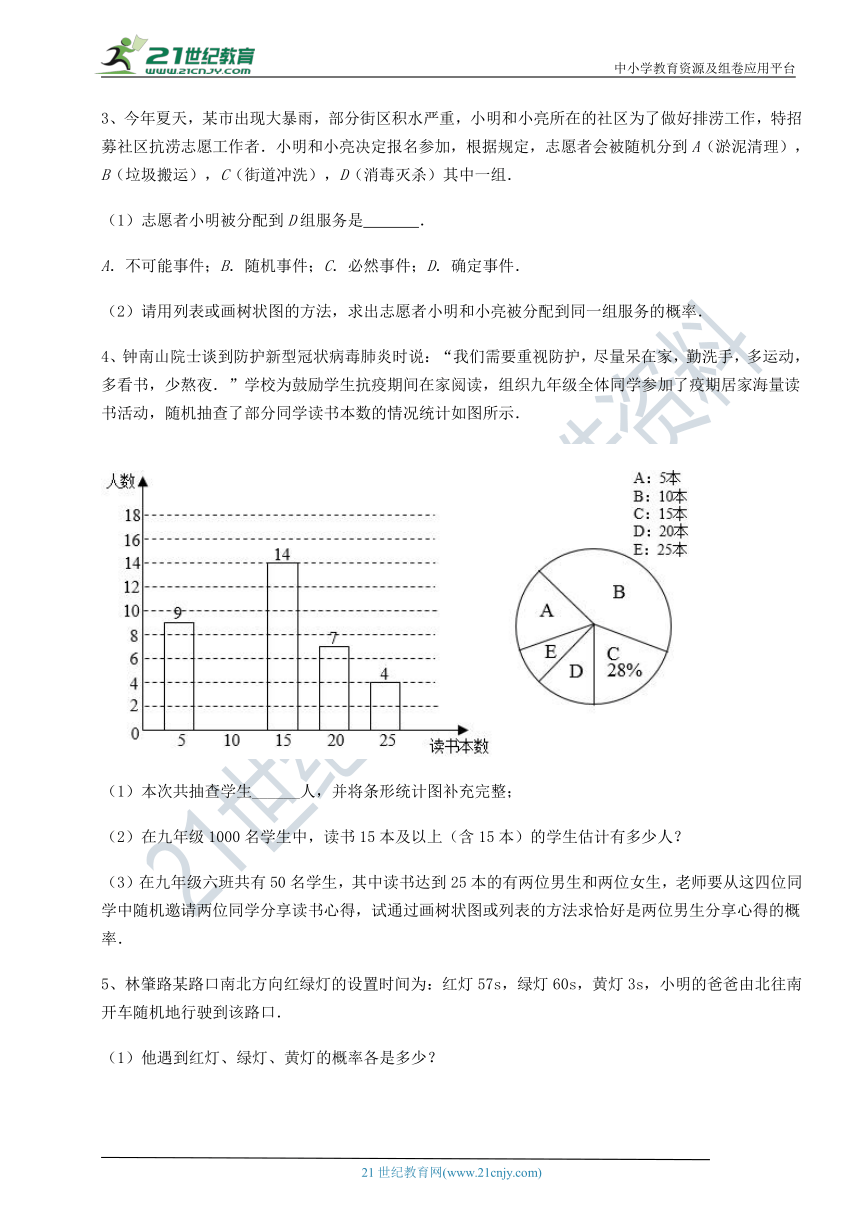
4、钟南山院士谈到防护新型 ( http: / / www.21cnjy.com )冠状病毒肺炎时说:“我们需要重视防护,尽量呆在家,勤洗手,多运动,多看书,少熬夜.”学校为鼓励学生抗疫期间在家阅读,组织九年级全体同学参加了疫期居家海量读书活动,随机抽查了部分同学读书本数的情况统计如图所示.
( http: / / www.21cnjy.com / )
(1)本次共抽查学生______人,并将条形统计图补充完整;
(2)在九年级1000名学生中,读书15本及以上(含15本)的学生估计有多少人?
(3)在九年级六班共有50名学生,其中 ( http: / / www.21cnjy.com )读书达到25本的有两位男生和两位女生,老师要从这四位同学中随机邀请两位同学分享读书心得,试通过画树状图或列表的方法求恰好是两位男生分享心得的概率.
5、林肇路某路口南北方向红绿灯的设置时间为:红灯57s,绿灯60s,黄灯3s,小明的爸爸由北往南开车随机地行驶到该路口.
(1)他遇到红灯、绿灯、黄灯的概率各是多少?
(2)我国新的交通法规定:汽车行驶到路 ( http: / / www.21cnjy.com )口时,绿灯亮时才能通过,如果遇到黄灯亮或红灯亮时必须在路口外停车等候,问小明的爸爸开车随机到该路口,按照交通信号灯直行停车等候的概率是多少?
-参考答案-
一、单选题
1、B
【分析】
根据统计图可知,试验结果在0.33附近波动,即其概率P≈0.33,计算四个选项的概率,约为0.33者即为正确答案.
【详解】
解:A、掷一枚正六面体的骰子,出现1点的概率为,故此选项不符合题意;
B、一个袋子中有2个白球和1个红球,从中任取一个球,则取到红球的概率≈0.33,故此选项符合题意;
C、掷一枚硬币,出现正面朝上的概率为,故此选项不符合题意;
D、任意写出一个整数,能被2整除的概率为,故此选项不符合题意.
故选:B.
【点睛】
此题考查了利用频率估计概率,大量反复 ( http: / / www.21cnjy.com )试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.同时此题在解答中要用到概率公式.
2、D
【分析】
根据必然事件的定义:在一定条件下,一定会发生的事件,进行逐一判断即可
【详解】
解:A、两次骰子的点数之和可能是奇数也可能是偶数,不是必然事件,不符合题意;
B、两次骰子的点数之和可能是奇数也可能是偶数,不是必然事件,不符合题意;
C、∵骰子的最大点数是12,∴两次点数之和不可能大于13,不是必然事件,不符合题意;
D、∵骰子的最大点数是12,∴两次点数之和小于13,是必然事件,符合题意;
故选D.
【点睛】
本题主要考查了必然事件的定义,熟知定义是解题的关键.
3、D
【分析】
根据事件发生的可能性大小判断相应事件的类型即可.
【详解】
解:“2022年年春节期间,中山市会下雨”这一事件为随机事件,
故选:D.
【点睛】
本题考查的是必然事件、不可能 ( http: / / www.21cnjy.com )事件、随机事件的概念,必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
4、D
【分析】
先列表展示所有可能的结果数为12,再找出两次摸出的球所标数字之积为6的结果数,然后根据概率的概念计算即可.21教育网
【详解】
解:列表如下:
( http: / / www.21cnjy.com / )
所有等可能的情况有12种,其中两次摸出的球所标数字之积为6的有4种结果,
所以两次摸出的球所标数字之积为6的概率为=.
故答案为:D
【点睛】
此题考查的是用列表法或树 ( http: / / www.21cnjy.com )状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
5、C
【分析】
根据大量重复试验后频率的稳定值即为概率,进行求解即可.
【详解】
解:∵一个口袋中有红色、黄色、蓝色玻璃球共200个,小明通过大量摸球试验后,发现摸到红球的频率为35%,
∴红球的个数=200×35%=70个,
故选C.
【点睛】
本题主要考查了用频率估计概率,解题的关键在于能够熟练掌握大量重复试验下,频率的稳定值即为概率.
6、D
【分析】
根据随机事件的定义:在一定条件下,可能发生也可能不发生的事件叫做随机事件,进行逐一判断即可.
【详解】
解:A、通常加热到100℃时,水沸腾,这是必然事件,不符合题意;
B、任意画一个三角形,其内角和是360°这是不可能事件,不符合题意;
C、三角形中,任意两边之和大于第三边,这是必然事件,不符合题意;
D、随意翻到一本书的某页,这页的页码是奇数,也可能是偶数,这是随机事件,符合题意;
故选D.
【点睛】
本题主要考查了随机事件的定义,熟知定义是解题的关键.
7、B
【分析】
由题意,只要求出阴影部分与矩形的面积比即可.
【详解】
解:由题意,假设每个小方砖的面积为1,则所有方砖的面积为15,而阴影部分的面积为5,
由几何概型公式得到最终停在阴影方砖上的概率为:;
故选:B.
【点睛】
本题将概率的求解设置于黑白方砖中,考查学 ( http: / / www.21cnjy.com )生对简单几何概率的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.用到的知识点为:概率=相应的面积与总面积之比.
8、D
【分析】
用A表示雄性,B表示雌性,画出树状图,共有4个等可能的结果,孵化出的小鸟恰有两个雌性一个雄性的结果有2个,然后根据概率公式计算即可.2-1-c-n-j-y
【详解】
解:用A表示雄性,B表示雌性,画树状图如图:
( http: / / www.21cnjy.com / )
共有4个等可能的结果,孵化出的小鸟恰有一个雌性一个雄性的结果有2个,
∴孵化出的小鸟恰有两个雌性一个雄性的概率为;
故选:D.
【点睛】
本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.
9、D
【分析】
根据概率的定义:概率表示事件发生可能性的大小,据此判断即可得.
【详解】
解:明天是晴天的概率为90%,说明明天是晴天的可能性很大,
故选:D.
【点睛】
题目主要考查概率的定义及对其的理解,深刻理解概率表示事件发生可能性的大小是解题关键.
10、A
【分析】
根据频率之和为1计算出白球的频率,然后再根据“数据总数×频率=频数”,算白球的个数即可.
【详解】
解:∵摸到红色球、黑色球的频率稳定在0.15和0.45,
∴摸到白球的频率为1-0.15-0.45=0.40,
∴口袋中白色球的个数可能是60×0.40=24个.
故选A.
【点睛】
本题考查了由频率估计概率,大量反复试验下频率稳定值即概率.根据频率之和为1计算出摸到白球的频率是解答本题的关键.21cnjy.com
二、填空题
1、
【分析】
袋中有五个小球,3个红球,2个白球,利用概率公式直接求解即可求得答案.
【详解】
解:袋中有五个小球,3个红球,2个白球,形状材料均相同,
从中任意摸一个球,摸出红球的概率为,
故答案是:.
【点睛】
本题考查概率的求法,解题的关键是掌握如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率(A).【版权所有:21教育】
2、
【分析】
首先画出树状图即可求得所有等可能的结果与点(a,b)在直线上的情况,然后利用概率公式求解即可求得答案.
【详解】
解:画树状图得:
( http: / / www.21cnjy.com / )
由树形图可知:一共有12种等可能的结果,其中点(a,b)在直线上的有3种结果,
所以点(a,b)在直线上的概率为,
故答案为:.
【点睛】
本题考查的是用列表法或画树状 ( http: / / www.21cnjy.com )图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
3、
【分析】
根据题意,使用列表法将所有可能性表示出来,然后找出满足条件的可能性计算概率即可.
【详解】
解:根据题意,使用列表法如下:
男 男 男 女
男 (男,男) (男,男) (男,女)
男 (男,男) (男,男) (男,女)
男 (男,男) (男,男) (男,女)
女 (女,男) (女,男) (女,男)
由表可得:共有12中可能,满足恰好抽取到1名男同学和1名女同学的共有6种可能性,
∴,
故答案为:.
【点睛】
题目主要考查利用树状图或者列表法表示出所有可能性,然后计算概率,熟练运用树状图或列表法是解题关键.
4、
【分析】
根据题意画树状图展示所有27种等可能的结果数,找出三人恰好进入同一社区的结果数,然后根据概率公式求解即可.21·cn·jy·com
【详解】
解:画树状图如图:
( http: / / www.21cnjy.com / )
共有27种等可能的结果数,其中三人恰好选择同一社区的结果为3种,
∴两人恰好选择同一社区的概率.
故答案为:.
【点睛】
本题考查列表法与树状图法:利 ( http: / / www.21cnjy.com )用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.【来源:21·世纪·教育·网】
5、
【分析】
根据概率公式计算即可
【详解】
共有个球,其中黑色球个
从中任意摸出一球,摸出黑色球的概率是.
解得
经检验,是原方程的解
故答案为:
【点睛】
本题考查了简单概率公式的计算,熟悉概率公式是解题的关键.概率=所求情况数与总情况数之比.
三、解答题
1、(1)见详解;(2).
【分析】
(1)根据题意通过列出相应的表格,即可得出所有可能结果;
(2)由题意利用取出的两个小球标号和等于5的结果数除以所有可能结果数即可得出答案.
【详解】
解:(1)由题意列表得:
1 2 3 4
1 --- (2,1) (3,1) (4,1)
2 (1,2) --- (3,2) (4,2)
3 (1,3) (2,3) --- (4,3)
4 (1,4) (2,4) (3,4) ---
所有可能的结果有12种;
(2)由(1)表格可知取出的两个小球标号和等于5的结果有(1,4)、(2,3)、(3,2)、(4,1)共4种,而所有可能的结果有12种,21世纪教育网版权所有
所以取出的两个小球标号和等于5的概率.
【点睛】
本题考查的是用列表法或树状图 ( http: / / www.21cnjy.com )法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.www-2-1-cnjy-com
2、(1);(2)
【分析】
(1)先列出树状图,找到所有的等可能性的结果数,然后找到两次摸出的球的标号相同的结果数,最后利用概率公式求解即可;21*cnjy*com
(2)根据(1)所列树状图,找到两次摸出的球的标号和为4的结果数,利用概率公式求解即可.
【详解】
解:(1)列树状图如下所示:
( http: / / www.21cnjy.com / )
由树状图可知一共有16种等可能性的结果数,其中两次摸出的球的标号相同的结果数有4种,
∴(两次摸出的球的标号相同);
(2)由树状图可知一共有16种等可能性的结果数,其中两次摸出的球的标号的和为4的结果数有(1,3),(2,2),(3,1)3种,
∴(两次摸出的球的标号的和等于4).
【点睛】
本题主要考查了树状图法或列表法求解概率,解题的关键在于能够熟练掌握树状图法或列表法求解概率.
3、(1)B;(2)志愿者小明和小亮被分配到同一组服务的概率.
【分析】
(1)根据志愿者会被随机分到A(淤泥清 ( http: / / www.21cnjy.com )理),B(垃圾搬运),C(街道冲洗),D(消毒灭杀)其中一组即可得出随机事件,随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件(简称事件);
(2)画树状图列出所有等可能的情况,从中找出符合条件的情况,然后利用概率公式计算即可.
【详解】
解:(1)∵志愿者会被随机分到A(淤泥清理),B(垃圾搬运),C(街道冲洗),D(消毒灭杀)其中一组,21·世纪*教育网
志愿者小明被分配到D组服务是:B.随机事件;
故答案为B;
(2)根据随机事件中出现所有等可能的结果共有16种,其中志愿者小明和小亮被分配到同一组共有4种情况,
∴志愿者小明和小亮被分配到同一组服务的概率.
( http: / / www.21cnjy.com / )
【点睛】
本题考查事件的识别,画树状图或列表求概率,掌握事件的识别方法,和画树状图方法,列举所有等可能的结果,熟记概率公式是解题关键.
4、(1)50,图见解析;(2)500人;(3)图表见解析,
【分析】
(1)由题意根据C的人数和所占的百分比,可以求得本次共抽查学生人数,然后即可计算出读书10本的人数,从而可以将条形统计图补充完整;
(2)由题意根据条形统计图中的数据,可以计算出读书15本及以上(含15本)的学生估计有多少人;
(3)根据题意,可以画出相应的树状图,从而可以求出恰好是两位男生分享心得的概率.
【详解】
解:(1)本次共抽查学生14÷28%=50(人),
故答案为:50;
50-9-14-7-4=16(人),
补全的条形统计图如图所示,
( http: / / www.21cnjy.com / )
(2)(人),
即读书15本及以上(含15本)的学生估计有500人.
(3)树状图如下图所示,
( http: / / www.21cnjy.com / )
一共有12种可能性,其中恰好是两位男生可能性有2种,
故恰好是两位男生分享心得的概率是.
【点睛】
本题考查列表法与树状图法、用样本估计总体、条形统计图、扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.21*cnjy*com
5、(1)他遇到红灯、绿灯、黄灯的概率各是、、;(2).
【分析】
(1)根据红灯、绿灯、黄灯的时间求出总时间,再利用概率公式即可得;
(2)将遇到红灯和黄灯的概率相加即可得.
【详解】
解:(1)红灯、绿灯、黄灯的总时间为,
则他遇到红灯的概率是,
遇到绿灯的概率是,
遇到黄灯的概率是,
答:他遇到红灯、绿灯、黄灯的概率各是、、;
(2),
答:按照交通信号灯直行停车等候的概率是.
【点睛】
本题考查了简单事件的概率,熟练掌握概率公式是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学第二学期第二十三章概率初步章节测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指 ( http: / / www.21cnjy.com )定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【来源:21cnj*y.co*m】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、甲、乙两位同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A.掷一枚正六面体的骰子,出现1点的概率
B.一个袋子中有2个白球和1个红球,从中任取一个球,则取到红球的概率
C.抛一枚硬币,出现正面的概率
D.任意写一个整数,它能被2整除的概率
2、同时抛两枚质地均匀的正方体骰子,骰子的六个面上分别刻有的点数,则下列事件中是必然事件的是( )21教育名师原创作品
A.点数之和为奇数 B.点数之和为偶数 C.点数之和大于 D.点数之和小于
3、 “2022年春节期间,中山市会下雨”这一事件为( )
A.必然事件 B.不可能事件 C.确定事件 D.随机事件
4、一个不透明的袋子中装 ( http: / / www.21cnjy.com )有四个小球,它们除了分别标有的数字1,2,3,6不同外,其他完全相同,任意从袋子中摸出一球后不放回,再任意摸出一球,则两次摸出的球所标数字之积为6的概率是( )
A. B. C. D.
5、一个口袋中有红色、黄色、蓝色玻璃球共200个,小明通过大量摸球试验后,发现摸到红球的频率为35%,则估计红球的个数约为( )
A.35个 B.60个 C.70个 D.130个
6、下列事件中,是随机事件的为( )
A.通常加热到100℃时,水沸腾
B.任意画一个三角形,其内角和是360°
C.三角形中,任意两边之和大于第三边
D.随意翻到一本书的某页,这页的页码是奇数
7、如图,一只小狗在如图所示的方砖上走来走去,最终停留在阴影方砖上的概率是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8、假如每个鸟卵都可以成功孵化小鸟,且孵化出 ( http: / / www.21cnjy.com )的小鸟是雄性和雌性的可能性相等.现有2枚鸟卵,孵化出的小鸟恰有一个雌性一个雄性的概率是( )2·1·c·n·j·y
A. B. C. D.
9、关于“明天是晴天的概率为90%”,下列说法正确的是( ).
A.明天一定是晴天 B.明天一定不是晴天
C.明天90%的地方是晴天 D.明天是晴天的可能性很大
10、在一个不透明的布袋中,红色、 ( http: / / www.21cnjy.com )黑色、白色的玻璃球共有60个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在0.15和0.45,则布袋中白色球的个数可能是( )
A.24 B.18 C.16 D.6
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、一个袋中有形状材料均相同的白球2个、红球3个,任意摸一个球是红球的概率_____.
2、四张背面相同的扑克牌,分别为红桃1,2,3,4,背面朝上,先从中抽取一张把抽到的点数记为a,再在剩余的扑克中抽取一张点数记为b,则以为坐标的点在直线上的概率为______.
3、综艺节目《朗读者》自开播以来受到大家 ( http: / / www.21cnjy.com )的广泛关注.重庆实验外国语学校某班主任准备从经常关注该节目的同学中抽取两人进行交流讨论,其中经常关注的同学中有3名男同学,1名女同学,则恰好抽取到1名男同学和1名女同学的概率是_________.
4、小张、小王和小李三人相 ( http: / / www.21cnjy.com )约去参加“抗疫情党员志愿者进社区服务”活动,现在有A、B、C三个社区可供随机选择,他们三人恰好进入同一社区的概率是____________.
5、在一个不透明的袋子中,装有若干个除颜色外都相同的小球,其中有8个红球和n个黑球,从袋中任意摸出一个球,若摸出黑球的概率是,则n=_____.
三、解答题(5小题,每小题10分,共计50分)
1、一个不透明的口袋中有四个分别标号为1,2,3,4的完全相同的小球,从中随机摸取两个小球.
(1)请列举出所有可能结果;
(2)求取出的两个小球标号和等于5的概率.
2、有4个完全相同的小球,把它们分别标号为1、2、3、4,放在一个口袋中,随机的摸出一个小球然后放回,再随机的摸出一个小球.www.21-cn-jy.com
(1)求两次摸出的球的标号相同的概率;
(2)求两次摸出的球的标号的和等于4的概率.
3、今年夏天,某市出现大暴雨,部分街区 ( http: / / www.21cnjy.com )积水严重,小明和小亮所在的社区为了做好排涝工作,特招募社区抗涝志愿工作者.小明和小亮决定报名参加,根据规定,志愿者会被随机分到A(淤泥清理),B(垃圾搬运),C(街道冲洗),D(消毒灭杀)其中一组.
(1)志愿者小明被分配到D组服务是 .
A.不可能事件;B.随机事件;C.必然事件;D.确定事件.
(2)请用列表或画树状图的方法,求出志愿者小明和小亮被分配到同一组服务的概率.
4、钟南山院士谈到防护新型 ( http: / / www.21cnjy.com )冠状病毒肺炎时说:“我们需要重视防护,尽量呆在家,勤洗手,多运动,多看书,少熬夜.”学校为鼓励学生抗疫期间在家阅读,组织九年级全体同学参加了疫期居家海量读书活动,随机抽查了部分同学读书本数的情况统计如图所示.
( http: / / www.21cnjy.com / )
(1)本次共抽查学生______人,并将条形统计图补充完整;
(2)在九年级1000名学生中,读书15本及以上(含15本)的学生估计有多少人?
(3)在九年级六班共有50名学生,其中 ( http: / / www.21cnjy.com )读书达到25本的有两位男生和两位女生,老师要从这四位同学中随机邀请两位同学分享读书心得,试通过画树状图或列表的方法求恰好是两位男生分享心得的概率.
5、林肇路某路口南北方向红绿灯的设置时间为:红灯57s,绿灯60s,黄灯3s,小明的爸爸由北往南开车随机地行驶到该路口.
(1)他遇到红灯、绿灯、黄灯的概率各是多少?
(2)我国新的交通法规定:汽车行驶到路 ( http: / / www.21cnjy.com )口时,绿灯亮时才能通过,如果遇到黄灯亮或红灯亮时必须在路口外停车等候,问小明的爸爸开车随机到该路口,按照交通信号灯直行停车等候的概率是多少?
-参考答案-
一、单选题
1、B
【分析】
根据统计图可知,试验结果在0.33附近波动,即其概率P≈0.33,计算四个选项的概率,约为0.33者即为正确答案.
【详解】
解:A、掷一枚正六面体的骰子,出现1点的概率为,故此选项不符合题意;
B、一个袋子中有2个白球和1个红球,从中任取一个球,则取到红球的概率≈0.33,故此选项符合题意;
C、掷一枚硬币,出现正面朝上的概率为,故此选项不符合题意;
D、任意写出一个整数,能被2整除的概率为,故此选项不符合题意.
故选:B.
【点睛】
此题考查了利用频率估计概率,大量反复 ( http: / / www.21cnjy.com )试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.同时此题在解答中要用到概率公式.
2、D
【分析】
根据必然事件的定义:在一定条件下,一定会发生的事件,进行逐一判断即可
【详解】
解:A、两次骰子的点数之和可能是奇数也可能是偶数,不是必然事件,不符合题意;
B、两次骰子的点数之和可能是奇数也可能是偶数,不是必然事件,不符合题意;
C、∵骰子的最大点数是12,∴两次点数之和不可能大于13,不是必然事件,不符合题意;
D、∵骰子的最大点数是12,∴两次点数之和小于13,是必然事件,符合题意;
故选D.
【点睛】
本题主要考查了必然事件的定义,熟知定义是解题的关键.
3、D
【分析】
根据事件发生的可能性大小判断相应事件的类型即可.
【详解】
解:“2022年年春节期间,中山市会下雨”这一事件为随机事件,
故选:D.
【点睛】
本题考查的是必然事件、不可能 ( http: / / www.21cnjy.com )事件、随机事件的概念,必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
4、D
【分析】
先列表展示所有可能的结果数为12,再找出两次摸出的球所标数字之积为6的结果数,然后根据概率的概念计算即可.21教育网
【详解】
解:列表如下:
( http: / / www.21cnjy.com / )
所有等可能的情况有12种,其中两次摸出的球所标数字之积为6的有4种结果,
所以两次摸出的球所标数字之积为6的概率为=.
故答案为:D
【点睛】
此题考查的是用列表法或树 ( http: / / www.21cnjy.com )状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
5、C
【分析】
根据大量重复试验后频率的稳定值即为概率,进行求解即可.
【详解】
解:∵一个口袋中有红色、黄色、蓝色玻璃球共200个,小明通过大量摸球试验后,发现摸到红球的频率为35%,
∴红球的个数=200×35%=70个,
故选C.
【点睛】
本题主要考查了用频率估计概率,解题的关键在于能够熟练掌握大量重复试验下,频率的稳定值即为概率.
6、D
【分析】
根据随机事件的定义:在一定条件下,可能发生也可能不发生的事件叫做随机事件,进行逐一判断即可.
【详解】
解:A、通常加热到100℃时,水沸腾,这是必然事件,不符合题意;
B、任意画一个三角形,其内角和是360°这是不可能事件,不符合题意;
C、三角形中,任意两边之和大于第三边,这是必然事件,不符合题意;
D、随意翻到一本书的某页,这页的页码是奇数,也可能是偶数,这是随机事件,符合题意;
故选D.
【点睛】
本题主要考查了随机事件的定义,熟知定义是解题的关键.
7、B
【分析】
由题意,只要求出阴影部分与矩形的面积比即可.
【详解】
解:由题意,假设每个小方砖的面积为1,则所有方砖的面积为15,而阴影部分的面积为5,
由几何概型公式得到最终停在阴影方砖上的概率为:;
故选:B.
【点睛】
本题将概率的求解设置于黑白方砖中,考查学 ( http: / / www.21cnjy.com )生对简单几何概率的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.用到的知识点为:概率=相应的面积与总面积之比.
8、D
【分析】
用A表示雄性,B表示雌性,画出树状图,共有4个等可能的结果,孵化出的小鸟恰有两个雌性一个雄性的结果有2个,然后根据概率公式计算即可.2-1-c-n-j-y
【详解】
解:用A表示雄性,B表示雌性,画树状图如图:
( http: / / www.21cnjy.com / )
共有4个等可能的结果,孵化出的小鸟恰有一个雌性一个雄性的结果有2个,
∴孵化出的小鸟恰有两个雌性一个雄性的概率为;
故选:D.
【点睛】
本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.
9、D
【分析】
根据概率的定义:概率表示事件发生可能性的大小,据此判断即可得.
【详解】
解:明天是晴天的概率为90%,说明明天是晴天的可能性很大,
故选:D.
【点睛】
题目主要考查概率的定义及对其的理解,深刻理解概率表示事件发生可能性的大小是解题关键.
10、A
【分析】
根据频率之和为1计算出白球的频率,然后再根据“数据总数×频率=频数”,算白球的个数即可.
【详解】
解:∵摸到红色球、黑色球的频率稳定在0.15和0.45,
∴摸到白球的频率为1-0.15-0.45=0.40,
∴口袋中白色球的个数可能是60×0.40=24个.
故选A.
【点睛】
本题考查了由频率估计概率,大量反复试验下频率稳定值即概率.根据频率之和为1计算出摸到白球的频率是解答本题的关键.21cnjy.com
二、填空题
1、
【分析】
袋中有五个小球,3个红球,2个白球,利用概率公式直接求解即可求得答案.
【详解】
解:袋中有五个小球,3个红球,2个白球,形状材料均相同,
从中任意摸一个球,摸出红球的概率为,
故答案是:.
【点睛】
本题考查概率的求法,解题的关键是掌握如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率(A).【版权所有:21教育】
2、
【分析】
首先画出树状图即可求得所有等可能的结果与点(a,b)在直线上的情况,然后利用概率公式求解即可求得答案.
【详解】
解:画树状图得:
( http: / / www.21cnjy.com / )
由树形图可知:一共有12种等可能的结果,其中点(a,b)在直线上的有3种结果,
所以点(a,b)在直线上的概率为,
故答案为:.
【点睛】
本题考查的是用列表法或画树状 ( http: / / www.21cnjy.com )图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
3、
【分析】
根据题意,使用列表法将所有可能性表示出来,然后找出满足条件的可能性计算概率即可.
【详解】
解:根据题意,使用列表法如下:
男 男 男 女
男 (男,男) (男,男) (男,女)
男 (男,男) (男,男) (男,女)
男 (男,男) (男,男) (男,女)
女 (女,男) (女,男) (女,男)
由表可得:共有12中可能,满足恰好抽取到1名男同学和1名女同学的共有6种可能性,
∴,
故答案为:.
【点睛】
题目主要考查利用树状图或者列表法表示出所有可能性,然后计算概率,熟练运用树状图或列表法是解题关键.
4、
【分析】
根据题意画树状图展示所有27种等可能的结果数,找出三人恰好进入同一社区的结果数,然后根据概率公式求解即可.21·cn·jy·com
【详解】
解:画树状图如图:
( http: / / www.21cnjy.com / )
共有27种等可能的结果数,其中三人恰好选择同一社区的结果为3种,
∴两人恰好选择同一社区的概率.
故答案为:.
【点睛】
本题考查列表法与树状图法:利 ( http: / / www.21cnjy.com )用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.【来源:21·世纪·教育·网】
5、
【分析】
根据概率公式计算即可
【详解】
共有个球,其中黑色球个
从中任意摸出一球,摸出黑色球的概率是.
解得
经检验,是原方程的解
故答案为:
【点睛】
本题考查了简单概率公式的计算,熟悉概率公式是解题的关键.概率=所求情况数与总情况数之比.
三、解答题
1、(1)见详解;(2).
【分析】
(1)根据题意通过列出相应的表格,即可得出所有可能结果;
(2)由题意利用取出的两个小球标号和等于5的结果数除以所有可能结果数即可得出答案.
【详解】
解:(1)由题意列表得:
1 2 3 4
1 --- (2,1) (3,1) (4,1)
2 (1,2) --- (3,2) (4,2)
3 (1,3) (2,3) --- (4,3)
4 (1,4) (2,4) (3,4) ---
所有可能的结果有12种;
(2)由(1)表格可知取出的两个小球标号和等于5的结果有(1,4)、(2,3)、(3,2)、(4,1)共4种,而所有可能的结果有12种,21世纪教育网版权所有
所以取出的两个小球标号和等于5的概率.
【点睛】
本题考查的是用列表法或树状图 ( http: / / www.21cnjy.com )法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.www-2-1-cnjy-com
2、(1);(2)
【分析】
(1)先列出树状图,找到所有的等可能性的结果数,然后找到两次摸出的球的标号相同的结果数,最后利用概率公式求解即可;21*cnjy*com
(2)根据(1)所列树状图,找到两次摸出的球的标号和为4的结果数,利用概率公式求解即可.
【详解】
解:(1)列树状图如下所示:
( http: / / www.21cnjy.com / )
由树状图可知一共有16种等可能性的结果数,其中两次摸出的球的标号相同的结果数有4种,
∴(两次摸出的球的标号相同);
(2)由树状图可知一共有16种等可能性的结果数,其中两次摸出的球的标号的和为4的结果数有(1,3),(2,2),(3,1)3种,
∴(两次摸出的球的标号的和等于4).
【点睛】
本题主要考查了树状图法或列表法求解概率,解题的关键在于能够熟练掌握树状图法或列表法求解概率.
3、(1)B;(2)志愿者小明和小亮被分配到同一组服务的概率.
【分析】
(1)根据志愿者会被随机分到A(淤泥清 ( http: / / www.21cnjy.com )理),B(垃圾搬运),C(街道冲洗),D(消毒灭杀)其中一组即可得出随机事件,随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件(简称事件);
(2)画树状图列出所有等可能的情况,从中找出符合条件的情况,然后利用概率公式计算即可.
【详解】
解:(1)∵志愿者会被随机分到A(淤泥清理),B(垃圾搬运),C(街道冲洗),D(消毒灭杀)其中一组,21·世纪*教育网
志愿者小明被分配到D组服务是:B.随机事件;
故答案为B;
(2)根据随机事件中出现所有等可能的结果共有16种,其中志愿者小明和小亮被分配到同一组共有4种情况,
∴志愿者小明和小亮被分配到同一组服务的概率.
( http: / / www.21cnjy.com / )
【点睛】
本题考查事件的识别,画树状图或列表求概率,掌握事件的识别方法,和画树状图方法,列举所有等可能的结果,熟记概率公式是解题关键.
4、(1)50,图见解析;(2)500人;(3)图表见解析,
【分析】
(1)由题意根据C的人数和所占的百分比,可以求得本次共抽查学生人数,然后即可计算出读书10本的人数,从而可以将条形统计图补充完整;
(2)由题意根据条形统计图中的数据,可以计算出读书15本及以上(含15本)的学生估计有多少人;
(3)根据题意,可以画出相应的树状图,从而可以求出恰好是两位男生分享心得的概率.
【详解】
解:(1)本次共抽查学生14÷28%=50(人),
故答案为:50;
50-9-14-7-4=16(人),
补全的条形统计图如图所示,
( http: / / www.21cnjy.com / )
(2)(人),
即读书15本及以上(含15本)的学生估计有500人.
(3)树状图如下图所示,
( http: / / www.21cnjy.com / )
一共有12种可能性,其中恰好是两位男生可能性有2种,
故恰好是两位男生分享心得的概率是.
【点睛】
本题考查列表法与树状图法、用样本估计总体、条形统计图、扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.21*cnjy*com
5、(1)他遇到红灯、绿灯、黄灯的概率各是、、;(2).
【分析】
(1)根据红灯、绿灯、黄灯的时间求出总时间,再利用概率公式即可得;
(2)将遇到红灯和黄灯的概率相加即可得.
【详解】
解:(1)红灯、绿灯、黄灯的总时间为,
则他遇到红灯的概率是,
遇到绿灯的概率是,
遇到黄灯的概率是,
答:他遇到红灯、绿灯、黄灯的概率各是、、;
(2),
答:按照交通信号灯直行停车等候的概率是.
【点睛】
本题考查了简单事件的概率,熟练掌握概率公式是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
