1.3.1 有理数的加法(第1课时) 教学课件 (共33张PPT)
文档属性
| 名称 | 1.3.1 有理数的加法(第1课时) 教学课件 (共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 23:01:58 | ||
图片预览







文档简介
(共33张PPT)
1.3.1有理数的加法
人教版七年级上册
教学目标
1.了解有理数加法的意义.
2.能运用有理数加法法则准确进行有理数的加法运算.
3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.
教学重、难点
1.重点:掌握有理数的加法法则,能运用法则进行加法运算.
2.难点:探究异号两数相加的法则.
新知导入
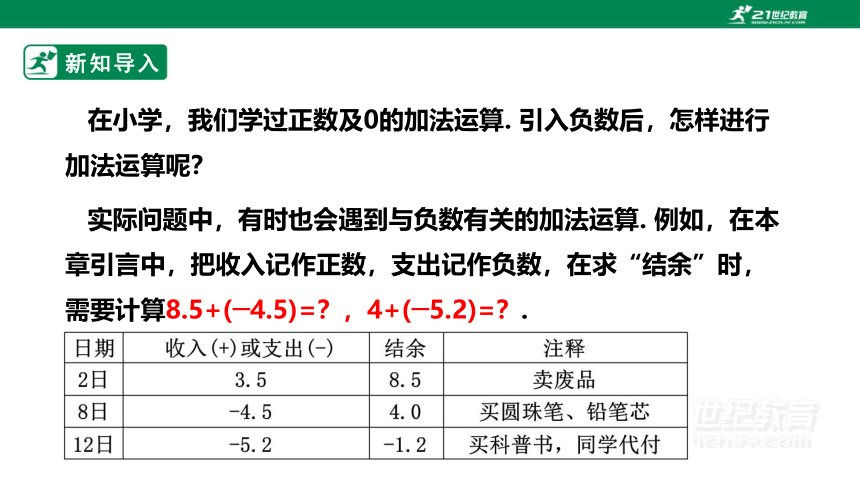
在小学,我们学过正数及0的加法运算. 引入负数后,怎样进行加法运算呢?
实际问题中,有时也会遇到与负数有关的加法运算. 例如,在本章引言中,把收入记作正数,支出记作负数,在求“结余”时,需要计算8.5+(─4.5)=?,4+(─5.2)=?.
新知讲解
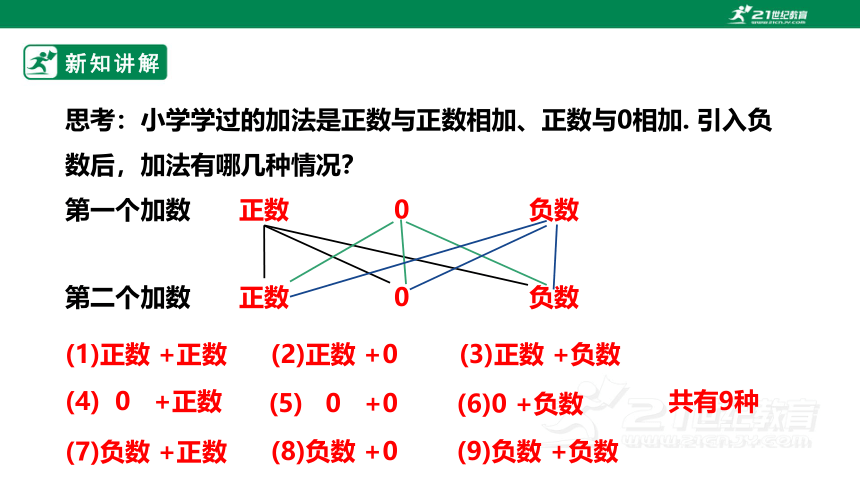
思考:小学学过的加法是正数与正数相加、正数与0相加. 引入负数后,加法有哪几种情况?
第一个加数
第二个加数
正数 0 负数
正数 0 负数
(1)正数 +正数
(2)正数 +0
(3)正数 +负数
(4) 0 +正数
(5) 0 +0
(6)0 +负数
(7)负数 +正数
(8)负数 +0
(9)负数 +负数
共有9种
新知讲解
这9种有理数加法,我们可以化归为几个类型?
(1)正数 +正数
(2)正数 +0
(3)正数 +负数
(4) 0 +正数
(5) 0 +0
(6)0 +负数
(7)负数 +正数
(8)负数 +0
(9)负数 +负数
三个类型:
一.同号两数相加
二.异号两数相加
三.一个数同0相加
(1)正数 +正数
(9)负数 +负数
(3)正数 +负数
(7)负数 +正数
(2)正数 +0
(4) 0 +正数
(5) 0 +0
(6)0 +负数
(8)负数 +0
新知讲解
引入负数后,我们可以把有理数加法化归为三个类型,下面借助具体情境和数轴来讨论有理数的加法.
我们规定向左为负,向右为正.向右运动5 m记作+5 m,向左运动5 m记作─5 m.
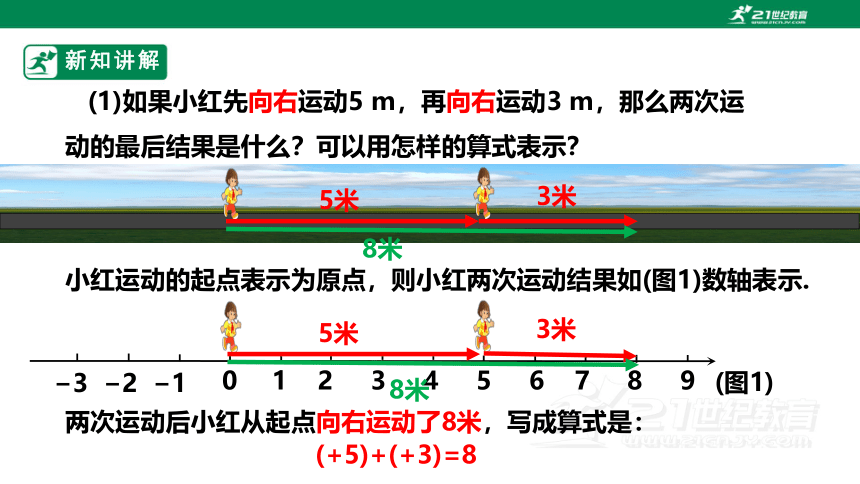
(1)如果小红先向右运动5 m,再向右运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
一.同号两数相加.
新知讲解
(1)如果小红先向右运动5 m,再向右运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图1)数轴表示.
0
1 2 3 4 5 6 7 8 9
3 2 1
(图1)
5米
3米
8米
5米
3米
8米
两次运动后小红从起点向右运动了8米,写成算式是:
(+5)+(+3)=8
新知讲解
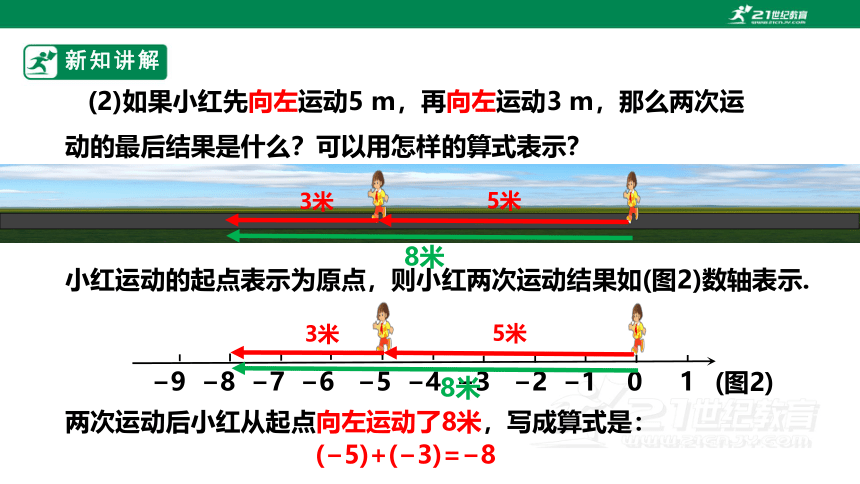
(2)如果小红先向左运动5 m,再向左运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图2)数轴表示.
9 8 7 6 5 4 3 2 1 0 1
(图2)
5米
3米
8米
两次运动后小红从起点向左运动了8米,写成算式是:
( 5)+( 3)= 8
5米
3米
8米
新知讲解
思考:同号两数相加,和的结果与两个加数什么关系?
(+5)+(+3)=+8
( 5)+( 3)= 8
正
和的符号与加数符号相同
正
加数符号相同
正
负
和的符号与加数符号相同
负
加数符号相同
负
归纳:同号两数相加,取相同的符号,
|5|+| 3|=8
| 5|+| 3|=8
数值:
并把绝对值相加.
新知讲解
例1: 计算:
(1). ( ─ 3)+( ─ 9)
(一判:同号两数相加)
解:(1)( ─ 3)+( ─ 9)
= ─( )
= ─ 12
(二定:取与加数相同的符号)
= ─( )
| ─ 3 |+| ─ 9 |
(三相加:把绝对值相加)
练一练
1. 计算: (1). ( ─ 2)+( ─ 11) (2). 15+(+7)
解:(1). ( ─ 2)+( ─ 11)
= ─ 13
= ─(| ─ 2 |+| ─ 11 | )
= ─(2+11)
(2). 15+(+7)
= 22
= +(| 15 |+| +7| )
= +(15+7)
(同号两数相加)
(取与加数相同的符号)
一判:
二定:
三相加:
(把绝对值相加)
注意:
新知讲解
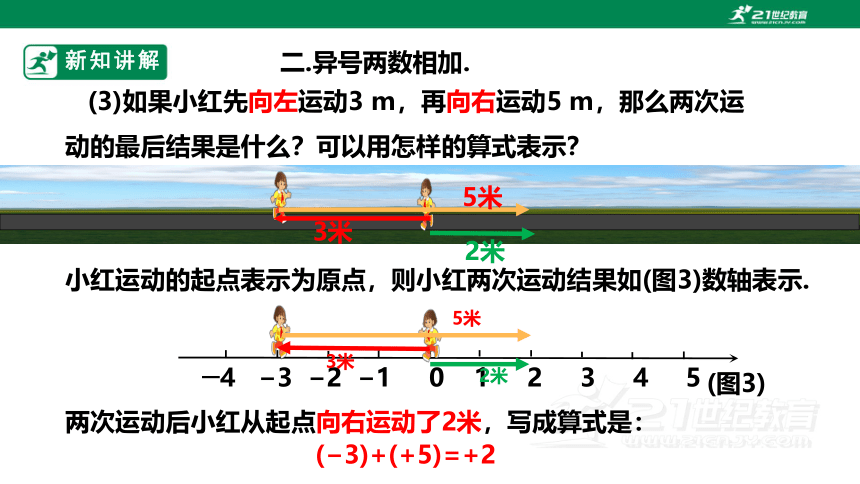
(3)如果小红先向左运动3 m,再向右运动5 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图3)数轴表示.
─4 3 2 1 0 1 2 3 4 5
(图3)
3米
5米
2米
3米
5米
2米
两次运动后小红从起点向右运动了2米,写成算式是:
( 3)+(+5)=+2
二.异号两数相加.
新知讲解
(4)如果小红先向右运动3 m,再向左运动5 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图4)数轴表示.
5 4 3 2 1 0 1 2 3 4 5
(图4)
3米
5米
2米
两次运动后小红从起点向左运动了2米,写成算式是:
(+3)+( 5)= 2
3米
5米
2米
新知讲解
思考:异号两数相加,和的结果与两个加数什么关系?
( 3)+(+5)=+2
(+3)+( 5)= 2
负
和的符号取绝对值较大的加数的符号
正
加数符号相反且| 3|<| +5|
正
正
和的符号取绝对值较大的加数的符号
负
加数符号相反且|+3|<| 5|
负
归纳:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
|+5| | 3|=2
| 5| |+3|=2
数值:
新知讲解
例1: 计算:(2)( ─ 4.7)+3.9
(一判:异号两数相加)
解:(2)( ─ 4.7)+3.9
= ─( )
= ─ 0.8
(二定:取绝对值较大的的符号)
= ─( )
| ─ 4.7 | ─ | 3.9 |
(三相减:用较大的绝对值减去
较大的绝对值)
练一练
1. 计算: (1). ( ─ 17)+ 13 (2). 0.5+(─ 1.7)
解: (1). ( ─ 17)+13
= ─ 4
= ─(| ─ 17 |─ | 13 | )
= ─(17─ 13)
(2). 0.5+(─ 1.7)
= ─ 1.2
= ─ (| ─ 1.7 |─ | 0.5| )
= ─ (1.7─ 0.5)
(异号两数相加)
(取绝对值较大的的符号)
一判:
二定:
三相减:
(用较大的绝对值减去
较大的绝对值)
注意:
归纳
3. 加减:最后进行绝对值的加减运算.
有理数加法运算的基本解题思路:
1.判:先判断类型(同号、异号等);
2.定:再确定和的符号;
新知讲解
(5)如果小红先向右运动5 m,再向左运动5 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图5)数轴表示.
5 4 3 2 1 0 1 2 3 4 5
(图5)
5米
5米
两次运动后小红从起点向右运动了0米,写成算式是:
(5)+( 5)=0
5米
5米
归纳
归纳总结:
互为相反数的两个数相加,结果为0.
新知讲解
(6)如果小红第1 s向右(或左)运动5 m,第2s原地不动,2s后小红从起点向右(或左)运动了5 m.如何用算式表示呢?
归纳总结:一个数同0相加,仍得这个数.
5 4 3 2 1 0 1 2 3 4 5
5 4 3 2 1 0 1 2 3 4 5
5+0= 5
(─5)+0=─5
归纳
有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
练一练
2.口算:
①(─4)+(─6)=_____ ②4+(─6)=_____ ③(─4)+6=_____ ④(─4)+4=_____ ⑤(─4)+14=_____ ⑥(─14)+4=_____
⑦6+(─6)=_____ ⑧0+(─6)=_____
1.用算式表示下面的结果:
(1)温度由─4℃上升7℃; ;
(2)收入7元,又支出5元. .
课本第18页练习
(─4)+7=3(℃)
(+7)+(─5)=2(元)
─10
─2
2
0
10
─10
0
─6
新知讲解
1. 计算5+(─3)的结果等于( )
A. 2 B. ─2
C. 5 D. 1
2. 下列哪一个数加上─5后,其绝对值大于13的是( )
A. 0 B. 16 C. ─8 D. ─9
B
D
新知讲解
3. 比─1大1的数是 ( )
A. ─1 B. 1 C. 0 D. ─2
4. 下列说法正确的是( )
A. 有理数分为正数和负数
B. 互为相反数的两个数的绝对值相等
C. 两数相加,和一定大于任何一个加数
D. 两数相加,和一定小于任何一个加数
C
B
新知讲解
5. 已知A地的海拔高度为─36米,B地比A地高20米,则B地的海拔高度为( ) .
A. 16米 B. 20米
C. ─16米 D. ─56米
6. 已知|a|=8,|b|=3,且|a─b|=b─a,则a+b的值为( ).
A. 5或11 B. ─5或─11
C. ─5 D. ─11
C
C
新知讲解
加数 加数 和的符号 和的绝对值 和
15 17
─15 ─17
─15 17
15 ─17
7.填表(想法则、写结果)
+
─
+
─
32
32
2
2
32
─32
2
─2
新知讲解
10.若a>0,b<0,|a|>|b|,则a+b_____0(用“>”或“<”填空).
8.大于─2.5而不大于3的整数的和为__________.
9.a为绝对值小于2022的所有整数的和,则a的值为___.
3
0
>
课堂练习
11. 为了迎接全国文明城市创建,市交警队的一辆警车在一条东西方向的公路上巡逻,如果规定向东为正,向西为负,从出发点开始所走的路程为:
+2,─3,+2,+1,─2,─1,─2(单位:千米)
(1)此时,这辆警车的司机如何向队长描述他的位置?
(2)如果此时距离出发点东侧2千米处出现交通事故,队长命令他马上赶往现场处置,则警车在此次巡逻和处理事故中共耗油多少升?(已知每千米耗油0.2升)
课堂练习
17. (1)解:
∵(+2)+(─3)+(+2)+(+1)+(─2)+(─1)+(─2)
∴这辆城管的汽车司机向队长描述他的位置为出发点以西3千米.
=─3(千米)
|+2|+|─3|+|+2|+|+1|+|─2|+|─1|+|─2|+|─3|+|+2|
(2)解:
=18(千米)
∴18×0.2=3.6(升)
∴这次出警共耗油3.6升.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
课堂总结
一.有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
3.一个数同0相加,仍得这个数.
3. 加减:最后进行绝对值的加减运算.
二.有理数加法运算的基本解题思路:
1.判:先判断类型(同号、异号等);
2.定:再确定和的符号;
作业布置
课本第24页
习题1.3
第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3.1有理数的加法
人教版七年级上册
教学目标
1.了解有理数加法的意义.
2.能运用有理数加法法则准确进行有理数的加法运算.
3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.
教学重、难点
1.重点:掌握有理数的加法法则,能运用法则进行加法运算.
2.难点:探究异号两数相加的法则.
新知导入
在小学,我们学过正数及0的加法运算. 引入负数后,怎样进行加法运算呢?
实际问题中,有时也会遇到与负数有关的加法运算. 例如,在本章引言中,把收入记作正数,支出记作负数,在求“结余”时,需要计算8.5+(─4.5)=?,4+(─5.2)=?.
新知讲解
思考:小学学过的加法是正数与正数相加、正数与0相加. 引入负数后,加法有哪几种情况?
第一个加数
第二个加数
正数 0 负数
正数 0 负数
(1)正数 +正数
(2)正数 +0
(3)正数 +负数
(4) 0 +正数
(5) 0 +0
(6)0 +负数
(7)负数 +正数
(8)负数 +0
(9)负数 +负数
共有9种
新知讲解
这9种有理数加法,我们可以化归为几个类型?
(1)正数 +正数
(2)正数 +0
(3)正数 +负数
(4) 0 +正数
(5) 0 +0
(6)0 +负数
(7)负数 +正数
(8)负数 +0
(9)负数 +负数
三个类型:
一.同号两数相加
二.异号两数相加
三.一个数同0相加
(1)正数 +正数
(9)负数 +负数
(3)正数 +负数
(7)负数 +正数
(2)正数 +0
(4) 0 +正数
(5) 0 +0
(6)0 +负数
(8)负数 +0
新知讲解
引入负数后,我们可以把有理数加法化归为三个类型,下面借助具体情境和数轴来讨论有理数的加法.
我们规定向左为负,向右为正.向右运动5 m记作+5 m,向左运动5 m记作─5 m.
(1)如果小红先向右运动5 m,再向右运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
一.同号两数相加.
新知讲解
(1)如果小红先向右运动5 m,再向右运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图1)数轴表示.
0
1 2 3 4 5 6 7 8 9
3 2 1
(图1)
5米
3米
8米
5米
3米
8米
两次运动后小红从起点向右运动了8米,写成算式是:
(+5)+(+3)=8
新知讲解
(2)如果小红先向左运动5 m,再向左运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图2)数轴表示.
9 8 7 6 5 4 3 2 1 0 1
(图2)
5米
3米
8米
两次运动后小红从起点向左运动了8米,写成算式是:
( 5)+( 3)= 8
5米
3米
8米
新知讲解
思考:同号两数相加,和的结果与两个加数什么关系?
(+5)+(+3)=+8
( 5)+( 3)= 8
正
和的符号与加数符号相同
正
加数符号相同
正
负
和的符号与加数符号相同
负
加数符号相同
负
归纳:同号两数相加,取相同的符号,
|5|+| 3|=8
| 5|+| 3|=8
数值:
并把绝对值相加.
新知讲解
例1: 计算:
(1). ( ─ 3)+( ─ 9)
(一判:同号两数相加)
解:(1)( ─ 3)+( ─ 9)
= ─( )
= ─ 12
(二定:取与加数相同的符号)
= ─( )
| ─ 3 |+| ─ 9 |
(三相加:把绝对值相加)
练一练
1. 计算: (1). ( ─ 2)+( ─ 11) (2). 15+(+7)
解:(1). ( ─ 2)+( ─ 11)
= ─ 13
= ─(| ─ 2 |+| ─ 11 | )
= ─(2+11)
(2). 15+(+7)
= 22
= +(| 15 |+| +7| )
= +(15+7)
(同号两数相加)
(取与加数相同的符号)
一判:
二定:
三相加:
(把绝对值相加)
注意:
新知讲解
(3)如果小红先向左运动3 m,再向右运动5 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图3)数轴表示.
─4 3 2 1 0 1 2 3 4 5
(图3)
3米
5米
2米
3米
5米
2米
两次运动后小红从起点向右运动了2米,写成算式是:
( 3)+(+5)=+2
二.异号两数相加.
新知讲解
(4)如果小红先向右运动3 m,再向左运动5 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图4)数轴表示.
5 4 3 2 1 0 1 2 3 4 5
(图4)
3米
5米
2米
两次运动后小红从起点向左运动了2米,写成算式是:
(+3)+( 5)= 2
3米
5米
2米
新知讲解
思考:异号两数相加,和的结果与两个加数什么关系?
( 3)+(+5)=+2
(+3)+( 5)= 2
负
和的符号取绝对值较大的加数的符号
正
加数符号相反且| 3|<| +5|
正
正
和的符号取绝对值较大的加数的符号
负
加数符号相反且|+3|<| 5|
负
归纳:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
|+5| | 3|=2
| 5| |+3|=2
数值:
新知讲解
例1: 计算:(2)( ─ 4.7)+3.9
(一判:异号两数相加)
解:(2)( ─ 4.7)+3.9
= ─( )
= ─ 0.8
(二定:取绝对值较大的的符号)
= ─( )
| ─ 4.7 | ─ | 3.9 |
(三相减:用较大的绝对值减去
较大的绝对值)
练一练
1. 计算: (1). ( ─ 17)+ 13 (2). 0.5+(─ 1.7)
解: (1). ( ─ 17)+13
= ─ 4
= ─(| ─ 17 |─ | 13 | )
= ─(17─ 13)
(2). 0.5+(─ 1.7)
= ─ 1.2
= ─ (| ─ 1.7 |─ | 0.5| )
= ─ (1.7─ 0.5)
(异号两数相加)
(取绝对值较大的的符号)
一判:
二定:
三相减:
(用较大的绝对值减去
较大的绝对值)
注意:
归纳
3. 加减:最后进行绝对值的加减运算.
有理数加法运算的基本解题思路:
1.判:先判断类型(同号、异号等);
2.定:再确定和的符号;
新知讲解
(5)如果小红先向右运动5 m,再向左运动5 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
小红运动的起点表示为原点,则小红两次运动结果如(图5)数轴表示.
5 4 3 2 1 0 1 2 3 4 5
(图5)
5米
5米
两次运动后小红从起点向右运动了0米,写成算式是:
(5)+( 5)=0
5米
5米
归纳
归纳总结:
互为相反数的两个数相加,结果为0.
新知讲解
(6)如果小红第1 s向右(或左)运动5 m,第2s原地不动,2s后小红从起点向右(或左)运动了5 m.如何用算式表示呢?
归纳总结:一个数同0相加,仍得这个数.
5 4 3 2 1 0 1 2 3 4 5
5 4 3 2 1 0 1 2 3 4 5
5+0= 5
(─5)+0=─5
归纳
有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
练一练
2.口算:
①(─4)+(─6)=_____ ②4+(─6)=_____ ③(─4)+6=_____ ④(─4)+4=_____ ⑤(─4)+14=_____ ⑥(─14)+4=_____
⑦6+(─6)=_____ ⑧0+(─6)=_____
1.用算式表示下面的结果:
(1)温度由─4℃上升7℃; ;
(2)收入7元,又支出5元. .
课本第18页练习
(─4)+7=3(℃)
(+7)+(─5)=2(元)
─10
─2
2
0
10
─10
0
─6
新知讲解
1. 计算5+(─3)的结果等于( )
A. 2 B. ─2
C. 5 D. 1
2. 下列哪一个数加上─5后,其绝对值大于13的是( )
A. 0 B. 16 C. ─8 D. ─9
B
D
新知讲解
3. 比─1大1的数是 ( )
A. ─1 B. 1 C. 0 D. ─2
4. 下列说法正确的是( )
A. 有理数分为正数和负数
B. 互为相反数的两个数的绝对值相等
C. 两数相加,和一定大于任何一个加数
D. 两数相加,和一定小于任何一个加数
C
B
新知讲解
5. 已知A地的海拔高度为─36米,B地比A地高20米,则B地的海拔高度为( ) .
A. 16米 B. 20米
C. ─16米 D. ─56米
6. 已知|a|=8,|b|=3,且|a─b|=b─a,则a+b的值为( ).
A. 5或11 B. ─5或─11
C. ─5 D. ─11
C
C
新知讲解
加数 加数 和的符号 和的绝对值 和
15 17
─15 ─17
─15 17
15 ─17
7.填表(想法则、写结果)
+
─
+
─
32
32
2
2
32
─32
2
─2
新知讲解
10.若a>0,b<0,|a|>|b|,则a+b_____0(用“>”或“<”填空).
8.大于─2.5而不大于3的整数的和为__________.
9.a为绝对值小于2022的所有整数的和,则a的值为___.
3
0
>
课堂练习
11. 为了迎接全国文明城市创建,市交警队的一辆警车在一条东西方向的公路上巡逻,如果规定向东为正,向西为负,从出发点开始所走的路程为:
+2,─3,+2,+1,─2,─1,─2(单位:千米)
(1)此时,这辆警车的司机如何向队长描述他的位置?
(2)如果此时距离出发点东侧2千米处出现交通事故,队长命令他马上赶往现场处置,则警车在此次巡逻和处理事故中共耗油多少升?(已知每千米耗油0.2升)
课堂练习
17. (1)解:
∵(+2)+(─3)+(+2)+(+1)+(─2)+(─1)+(─2)
∴这辆城管的汽车司机向队长描述他的位置为出发点以西3千米.
=─3(千米)
|+2|+|─3|+|+2|+|+1|+|─2|+|─1|+|─2|+|─3|+|+2|
(2)解:
=18(千米)
∴18×0.2=3.6(升)
∴这次出警共耗油3.6升.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
课堂总结
一.有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
3.一个数同0相加,仍得这个数.
3. 加减:最后进行绝对值的加减运算.
二.有理数加法运算的基本解题思路:
1.判:先判断类型(同号、异号等);
2.定:再确定和的符号;
作业布置
课本第24页
习题1.3
第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
