八上第二章实数复习课件

课件18张PPT。第二章 实数复习北师大版数学八年级（上册）

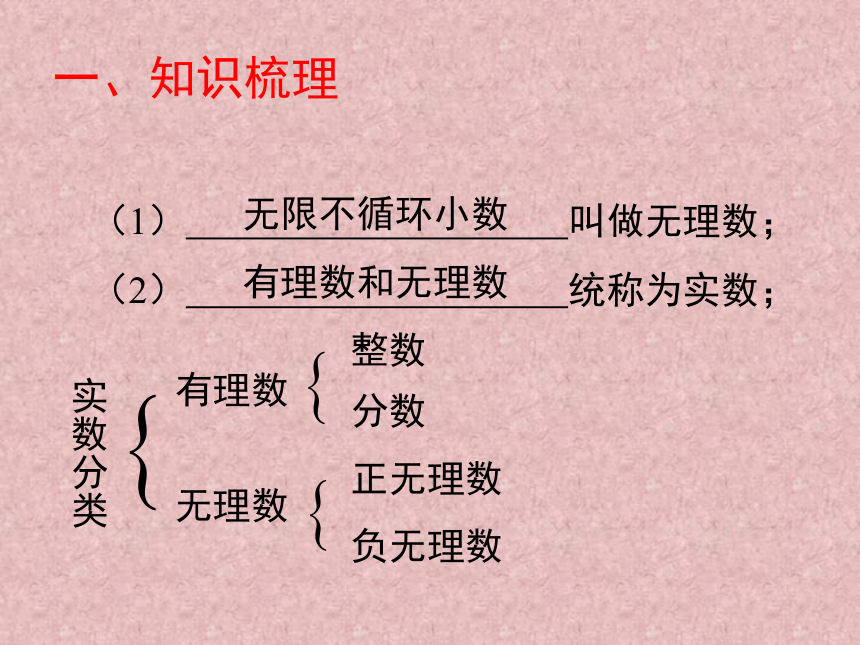
一、知识梳理
（1） 叫做无理数；
（2） 统称为实数；实数分类有理数无理数整数分数正无理数负无理数无限不循环小数有理数和无理数（3） 和数轴上的点是一一对应的；（4）实数（5）把 中的根号化去，叫做分母有理化；
（6）最简二次根式应满足的条件是：
被开方数 ，
也不含 . 不含分母能开得尽方的因数或因式分母 （7）同类二次根式：几个二次根式化成 后，如果被开方数相同，这几个二次根式就叫做同类二次根式；化简时，有同类二次根式要合并，可以约分的分式要约分。最简二次根式二、典例精析（一）实数的相关概念 例1 下列各数中，哪些是有理数，哪些是无理数？ ， ，3.14159265， ， ，
， ，3.1010010001…（相邻两个1之间0的各数逐次加1）
例1 下列各数中，哪些是有理数，哪些是无理数？ ， ，3.14159265， ， ，
， ，3.1010010001…（相邻两个1之间0的各数逐次加1）
有理数的判断方法： 整数和分数 无限不循环的小数 主要有以下几种： 例1 下列各数中，哪些是有理数，哪些是无理数？ ， ，3.14159265， ， ，
， ，3.1010010001…（相邻两个1之间0的各数逐次加1）
无理数的判断方法： ①开方开不尽的方根 ③是无限小数且不循环 例1 下列各数中，哪些是有理数，哪些是无理数？ ， ，3.14159265， ， ，
， ，3.1010010001…（相邻两个1之间0的各数逐次加1）
此题中的有理数：此题中的无理数：（二）实数的相关性质及运算 例2 实数 ， 在数轴上的位置如图所示，化简 .例3 计算：
(1) （2） 解：原式解：原式解： 解：
（三）实数中的数形结合 例5 已知△ABC中，AB=17，AC=10，BC边上的高AD=8，则边BC的长为多少？分析：（1）当△ABC为锐角三角形时，易求BD=15，DC=6，从而求得BC=15+6=21.（2）当△ABC为钝角三角形时，易求BD=15，DC=6，从而求得BC=15－6=9. 三、运用巩固1．下列说法错误的是（ ）A．4的算术平方根是2 B ． 是2的平方根 C．－1的立方根是－1 D．－3是 的平方根 D2四、课堂小结请同学们认真思考下列问题：
1．通过本堂课的学习我收获了什么？
2．我还有哪些没有解决的困惑？五、课后作业 完成课本 复习题知识技能1题、4题、10题；数学理解14题；问题解决21题.