22.1.1 二次函数 课件(共21张PPT)
文档属性
| 名称 | 22.1.1 二次函数 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 674.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 08:12:24 | ||
图片预览






文档简介
(共21张PPT)
22.1.1 二次函数
(2)你们知道:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
(1)我们有很多同学都喜欢打篮球!
函数:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就说y是x的函数, x是自变量.
函数
一次函数
y=kx+b (k≠0)
(正比例函数) y=kx (k≠0)
温故知新
……
合作探究
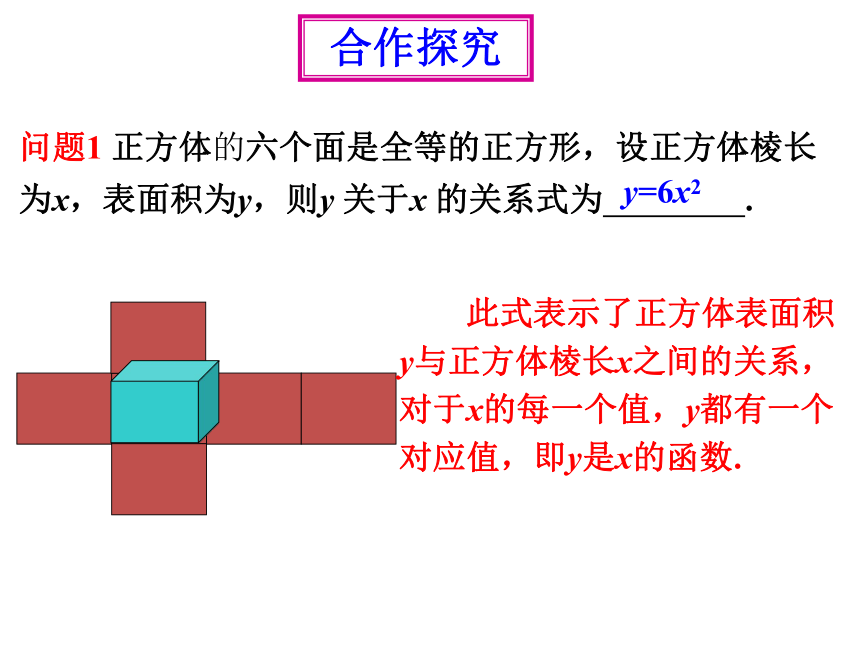
问题1 正方体的六个面是全等的正方形,设正方体棱长为x,表面积为y,则y 关于x 的关系式为 .
y=6x2
此式表示了正方体表面积y与正方体棱长x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
合作探究
合作探究
问题2 n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
分析:每个球队n要与其他 个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛是同一场比赛,所以比赛的场次数为 .
(n-1)
解:
此式表示了比赛的场次数m与球队数n之间的关系,对于n的每一个值,m都有一个对应值,即m是n的函数.
合作探究
合作探究
问题3 某种产品现在的年产量是20 t,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系怎样表示?
分析:这种产品的原产量是20 t,一年后的产量 t,再经过一年后的产量是 t,即两年后的产量y= .
20(1+x)
20(1+x)2
解:
y=20x2+40x+20;
此式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
20(1+x)(1+x)
合作探究
合作探究
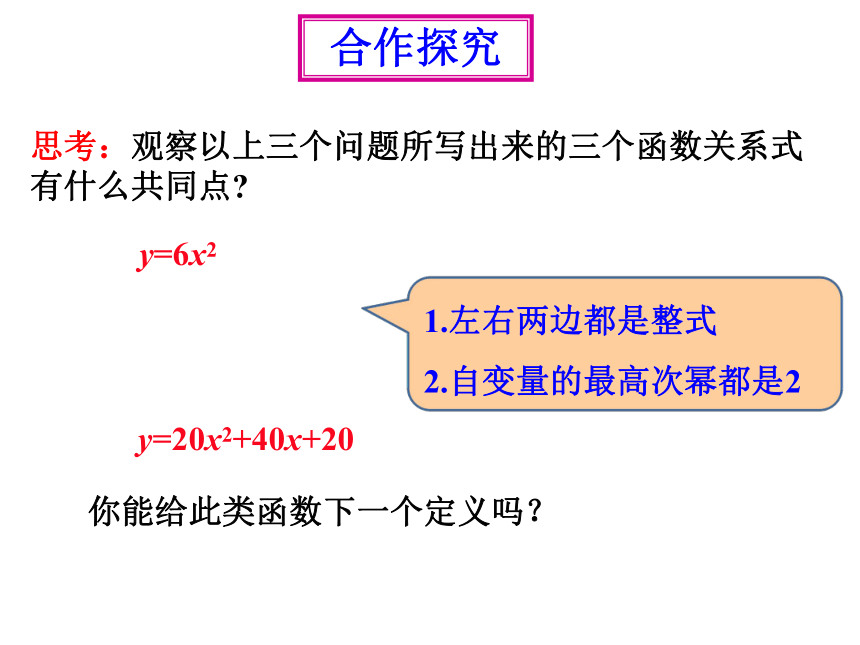
y=6x2
y=20x2+40x+20
思考:观察以上三个问题所写出来的三个函数关系式有什么共同点
你能给此类函数下一个定义吗?
1.左右两边都是整式
2.自变量的最高次幂都是2
合作探究
合作探究
二次函数的定义:
一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数.其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
二次函数的特征条件:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项.
形成概念
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
二次函数一般式:y=ax2+bx+c (a,b,c为常数,a≠0)
深度理解
思考:二次函数的一般式 y=ax2+bx+c(a≠0)与一元二次方程 ax2+bx+c=0(a≠0)有什么联系和区别?
联系:(1)等式一边都是ax2+bx+c且a ≠0;
(2)方程 ax2+bx+c=0 可以看成是函数 y= ax2+bx+c 中
y=0 时得到的.
区别:前者是函数,后者是方程.等式另一边前者是 y,后者是0.
深度理解
合作探究
1.下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项.
(1)y=x -x+2
(2)y=3(x-1) +1
(3)
(4)s=3-2t
(5)y=(x+1) -x
(6)S=πr
(7)y=ax2
√ 二次项系数:3,一次项系数:-6,常数项:4
×
√ 二次项系数:-2,一次项系数:0,常数项:3
× 先整理化简后,再作判断
√ 二次项系数:π,一次项系数:0,常数项:0
× 必须a≠0
感悟新知
√ 二次项系数:1,一次项系数:-1,常数项:2
2.函数y=(m-2)x2+mx-3(m为常数).
(1)当m_________时,该函数为二次函数;
(2)当m_________时,该函数为一次函数.
感悟新知
≠2
=2
变式:关于x的函数 是二次函数,求m的值.
解: 由题意可得
注意 :二次函数的二次项系数不能为0.
感悟新知
1.已知二次函数y=x +px+q,当x=1时,函数值为4;当x=2时,函数值为-5,求这个二次函数的解析式.
解,得 p=-12,q=15
知识应用
解:∵当x=1时,函数值为4;当x=2时,函数值为-5,
2.用20米的篱笆围一个矩形的花圃设连墙的一边为x,矩形的面积为y,求:(1)写出y关于x的函数关系式和自变量x的取值范围.(2)当x=3时,矩形的面积为多少
(2)当x=3时
(0答:当x=3时,矩形的面积为42m2.
x
知识应用
1. 下列函数是二次函数的是( )
A. y=3x-1 B. y=x3-2x-3
C. y=(x+1)2-x2 D. y=3x2
2. 二次函数y=3x2+2x-4的二次项系数与常数项分别
是( )
A.3,2 B.3,-4 C.2,-4 D.3,4
D
B
课堂检测
5. 一个圆柱的高等于底面半径,写出它的表面积 S 与底面半径 r 之间的关系式_______.
S=4πr2
3.已知函数y=(a-1)x2+3x-1,若y是x的二次函数,
则a的取值范围是 .
a≠1
课堂检测
4.在一定条件下,若物体运动的路段s(米)与时间t(秒)之间的关系为s=5t2+2t,则当t=4秒时,该物体所经过的路程为 .
88
合作探究
5.如图,矩形绿地的长、宽各增加 x m,写出扩充后的绿地的面积 y 与 x 的关系式.
解:由题意知
扩充后的绿地的面积是y=(30+x)(20+x)=x2+50x+600,
即 y=x2+50x+600.
30 m
x m
20 m
x m
课堂检测
综合演练
6.已知y与x2成正比例,且当x=3时,y=-18,写出y与x之间的函数解析式,它是二次函数吗?
解:∵y与x2成正比例,
∴y=kx2(k≠0),
把x=3,y=-18代入得:-18=32 k,
∴k=-2,
∴y与x之间的函数解析式为 y=-2x2.
符合二次函数的定义,属于二次函数.
课堂检测
问题导入,列关系式
探索二次关系式共同点
总结二次函数概念
二次函数y=ax +bx+c
(a,b,c为常数,a≠0)
二次函数的判别:
①含未知数的代数式为整式;
②未知数最高次数为2;
③二次项系数不为0.
确定二次函数解析式及自变量的取值范围
小结提升
如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,写出△PBQ的面积S与出发时间t(s)的函数关系式及t的取值范围.
解:依题意,得AP=2t, BQ=4t.
∵AB=12, ∴PB=12-2t,
t的取值范围为0≤t≤6.
∴
∴
拓展提升
22.1.1 二次函数
(2)你们知道:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
(1)我们有很多同学都喜欢打篮球!
函数:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就说y是x的函数, x是自变量.
函数
一次函数
y=kx+b (k≠0)
(正比例函数) y=kx (k≠0)
温故知新
……
合作探究
问题1 正方体的六个面是全等的正方形,设正方体棱长为x,表面积为y,则y 关于x 的关系式为 .
y=6x2
此式表示了正方体表面积y与正方体棱长x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
合作探究
合作探究
问题2 n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
分析:每个球队n要与其他 个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛是同一场比赛,所以比赛的场次数为 .
(n-1)
解:
此式表示了比赛的场次数m与球队数n之间的关系,对于n的每一个值,m都有一个对应值,即m是n的函数.
合作探究
合作探究
问题3 某种产品现在的年产量是20 t,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系怎样表示?
分析:这种产品的原产量是20 t,一年后的产量 t,再经过一年后的产量是 t,即两年后的产量y= .
20(1+x)
20(1+x)2
解:
y=20x2+40x+20;
此式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
20(1+x)(1+x)
合作探究
合作探究
y=6x2
y=20x2+40x+20
思考:观察以上三个问题所写出来的三个函数关系式有什么共同点
你能给此类函数下一个定义吗?
1.左右两边都是整式
2.自变量的最高次幂都是2
合作探究
合作探究
二次函数的定义:
一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数.其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
二次函数的特征条件:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项.
形成概念
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
二次函数一般式:y=ax2+bx+c (a,b,c为常数,a≠0)
深度理解
思考:二次函数的一般式 y=ax2+bx+c(a≠0)与一元二次方程 ax2+bx+c=0(a≠0)有什么联系和区别?
联系:(1)等式一边都是ax2+bx+c且a ≠0;
(2)方程 ax2+bx+c=0 可以看成是函数 y= ax2+bx+c 中
y=0 时得到的.
区别:前者是函数,后者是方程.等式另一边前者是 y,后者是0.
深度理解
合作探究
1.下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项.
(1)y=x -x+2
(2)y=3(x-1) +1
(3)
(4)s=3-2t
(5)y=(x+1) -x
(6)S=πr
(7)y=ax2
√ 二次项系数:3,一次项系数:-6,常数项:4
×
√ 二次项系数:-2,一次项系数:0,常数项:3
× 先整理化简后,再作判断
√ 二次项系数:π,一次项系数:0,常数项:0
× 必须a≠0
感悟新知
√ 二次项系数:1,一次项系数:-1,常数项:2
2.函数y=(m-2)x2+mx-3(m为常数).
(1)当m_________时,该函数为二次函数;
(2)当m_________时,该函数为一次函数.
感悟新知
≠2
=2
变式:关于x的函数 是二次函数,求m的值.
解: 由题意可得
注意 :二次函数的二次项系数不能为0.
感悟新知
1.已知二次函数y=x +px+q,当x=1时,函数值为4;当x=2时,函数值为-5,求这个二次函数的解析式.
解,得 p=-12,q=15
知识应用
解:∵当x=1时,函数值为4;当x=2时,函数值为-5,
2.用20米的篱笆围一个矩形的花圃设连墙的一边为x,矩形的面积为y,求:(1)写出y关于x的函数关系式和自变量x的取值范围.(2)当x=3时,矩形的面积为多少
(2)当x=3时
(0
x
知识应用
1. 下列函数是二次函数的是( )
A. y=3x-1 B. y=x3-2x-3
C. y=(x+1)2-x2 D. y=3x2
2. 二次函数y=3x2+2x-4的二次项系数与常数项分别
是( )
A.3,2 B.3,-4 C.2,-4 D.3,4
D
B
课堂检测
5. 一个圆柱的高等于底面半径,写出它的表面积 S 与底面半径 r 之间的关系式_______.
S=4πr2
3.已知函数y=(a-1)x2+3x-1,若y是x的二次函数,
则a的取值范围是 .
a≠1
课堂检测
4.在一定条件下,若物体运动的路段s(米)与时间t(秒)之间的关系为s=5t2+2t,则当t=4秒时,该物体所经过的路程为 .
88
合作探究
5.如图,矩形绿地的长、宽各增加 x m,写出扩充后的绿地的面积 y 与 x 的关系式.
解:由题意知
扩充后的绿地的面积是y=(30+x)(20+x)=x2+50x+600,
即 y=x2+50x+600.
30 m
x m
20 m
x m
课堂检测
综合演练
6.已知y与x2成正比例,且当x=3时,y=-18,写出y与x之间的函数解析式,它是二次函数吗?
解:∵y与x2成正比例,
∴y=kx2(k≠0),
把x=3,y=-18代入得:-18=32 k,
∴k=-2,
∴y与x之间的函数解析式为 y=-2x2.
符合二次函数的定义,属于二次函数.
课堂检测
问题导入,列关系式
探索二次关系式共同点
总结二次函数概念
二次函数y=ax +bx+c
(a,b,c为常数,a≠0)
二次函数的判别:
①含未知数的代数式为整式;
②未知数最高次数为2;
③二次项系数不为0.
确定二次函数解析式及自变量的取值范围
小结提升
如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,写出△PBQ的面积S与出发时间t(s)的函数关系式及t的取值范围.
解:依题意,得AP=2t, BQ=4t.
∵AB=12, ∴PB=12-2t,
t的取值范围为0≤t≤6.
∴
∴
拓展提升
同课章节目录
