人教版九年级上册数学22.3实际问题与二次函数同步训练(Word版含答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数同步训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 00:00:00 | ||
图片预览


文档简介
人教版九年级上册数学22.3 实际问题与二次函数同步训练
一、单选题
1.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
2.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
3.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
4.在中考体育训练期间,小学对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为y=-+x+,由此可知小宇此次实心球训练的成绩为( )
A.米 B.2米 C.8米 D.10米
5.某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,DA⊥OB,垂足为A.已知OC=OB=8m,OA=2m,则该水流距水平面的最大高度AD的长度为( ).
A.9m B.10m C.11m D.12m
6.为响应国家的惠民政策,某种口罩原价每箱100元,经过两次降价后每箱81元.设平均每次降价的百分率都为x,则x满足( )
A.81(1+2x)= 100 B.100(1-2x)=81
C.81(1+x)=100 D.100(1-x)=81
7.某商场降价销售一批名牌衬衫,已知所获得利润(元)与降价金额(元)之间的关系是,则获利最多为()
A.元 B.元 C.元 D.元
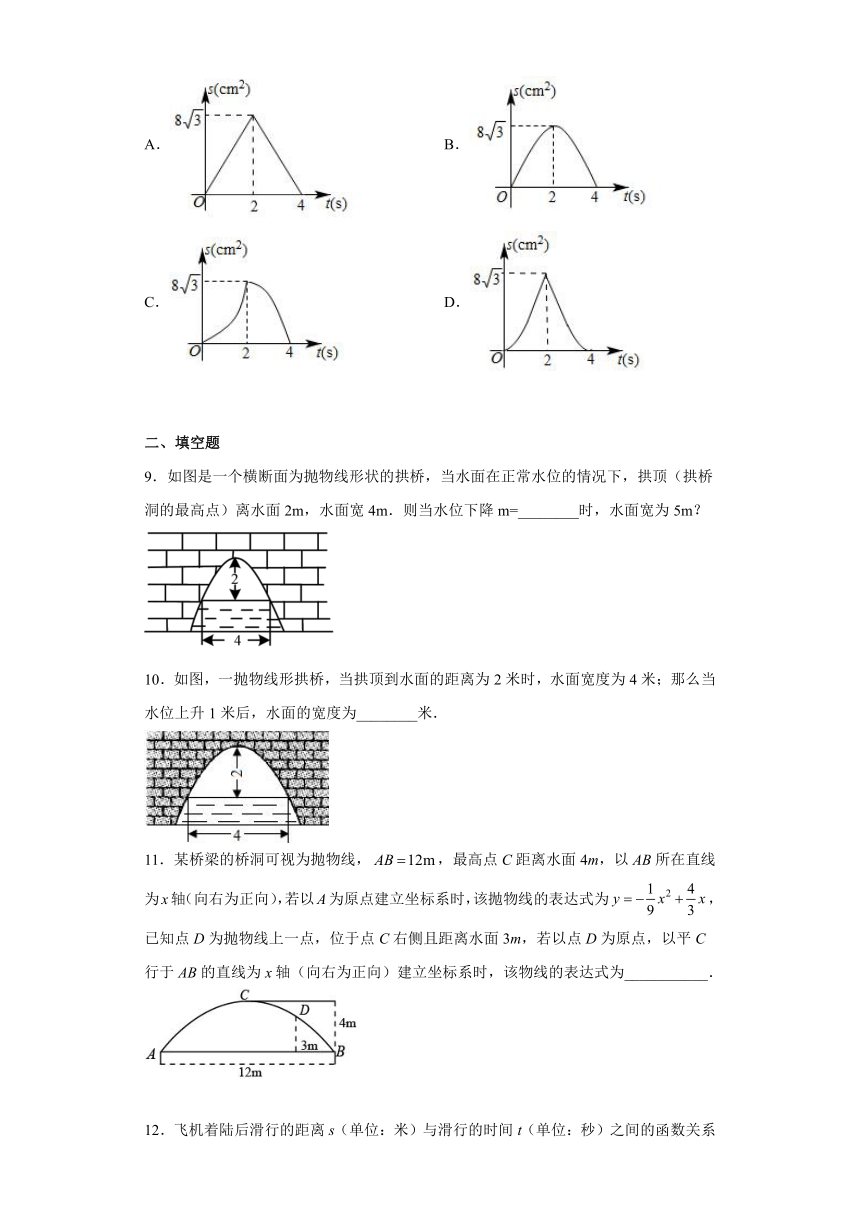
8.如图,中,,,直线经过点B且直线,直线从点B出发以的速度沿向右匀速移动,直到直线过点C时停止移动.移动过程中,直线交于点M,交或于点N,设的面积为,直线运动时间为,则下列最能反映S与t之间函数关系的图象是( )
A. B.
C. D.
二、填空题
9.如图是一个横断面为抛物线形状的拱桥,当水面在正常水位的情况下,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.则当水位下降m=________时,水面宽为5m?
10.如图,一抛物线形拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位上升1米后,水面的宽度为________米.
11.某桥梁的桥洞可视为抛物线,,最高点C距离水面4m,以AB所在直线为x轴(向右为正向),若以A为原点建立坐标系时,该抛物线的表达式为,已知点D为抛物线上一点,位于点C右侧且距离水面3m,若以点D为原点,以平C行于AB的直线为x轴(向右为正向)建立坐标系时,该物线的表达式为___________.
12.飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是,飞机着陆后滑行_____秒才能停下来.
13.赵州桥的桥拱横截面是近似的抛物线形,其示意图如图所示,其解析式为y=﹣x2.当水面离桥拱顶的高度DO为4m时,水面宽度AB为____m.
14.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=﹣1.2x2+48x,该型号飞机着陆后需滑行_____m才能停下来.
15.某品牌裙子,平均每天可以售出20条,每条盈利40元,经市场调查发现,如果该品牌每条裙子每降价1元,那么平均每天可以多售出2条,那么当裙子降价_________元时,可获得最大利润__________
16.抛出的一小球飞行的高度y与飞行时间x之间满足:,则该小球第2秒时的高度与第_______秒时的高度相同.
三、解答题
17.如图,某中学课外活动小组准备围建一个矩形苗圃园.其中一边靠墙,另外三边用长为20米的篱笆围成.已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.
(1)若这个苗圃园的面积为S平方米,求出S与x之间的函数关系式,并写出自变量x的取值范围;
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大面积.
18.“国庆节期间”某商场销售一款商品,每件的成本是元.销售期间发现:销售单价是元时,每天销售量是件,而销售单价每降低元,每天就可多售出件.但要求销售单价不得低于成本.设当销售单价为元时,每天销售利润为元.
(1)求与之间的函数表达式.
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果每天的销售利润不低于元,那么每天的总成本至少需要 元.
19.某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现:若每箱以50元的价格出售,平均每天销售80箱,价格每提高1元,平均每天少销售2箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
20.为了落实国务院的指示精神,某地方政府出台了一系列“精准扶贫”优惠政策,使贫困户收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量(千克)与销售价(元/千克)有如下关系:.设这种产品每天的销售利润为元.
(1)求与之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克30元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
试卷第3页,共5页
参考答案:
1.D
2.C
3.A
4.C
5.A
6.D
7.D
8.C
9.
10.
11.##
12.
13.20
14.480
15. 15 1250
16.4
17.(1)S=-2x2+20x(1≤x<10)
(2)当矩形苗圃园垂直于墙的边长为5米时,这个苗圃园的面积最大,最大面积为50平方米
18.(1)
(2)元,最大利润元
(3)
19.(1)y=﹣2x+180
(2)w=﹣2x2+260x﹣7200
(3)55元,1050元
20.(1)w=-2x2+120x-1600
(2)销售价定为每千克30元时,每天销售利润最大,最大销售利润200元
(3)每千克25元
答案第1页,共2页
一、单选题
1.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
2.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
3.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
4.在中考体育训练期间,小学对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为y=-+x+,由此可知小宇此次实心球训练的成绩为( )
A.米 B.2米 C.8米 D.10米
5.某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,DA⊥OB,垂足为A.已知OC=OB=8m,OA=2m,则该水流距水平面的最大高度AD的长度为( ).
A.9m B.10m C.11m D.12m
6.为响应国家的惠民政策,某种口罩原价每箱100元,经过两次降价后每箱81元.设平均每次降价的百分率都为x,则x满足( )
A.81(1+2x)= 100 B.100(1-2x)=81
C.81(1+x)=100 D.100(1-x)=81
7.某商场降价销售一批名牌衬衫,已知所获得利润(元)与降价金额(元)之间的关系是,则获利最多为()
A.元 B.元 C.元 D.元
8.如图,中,,,直线经过点B且直线,直线从点B出发以的速度沿向右匀速移动,直到直线过点C时停止移动.移动过程中,直线交于点M,交或于点N,设的面积为,直线运动时间为,则下列最能反映S与t之间函数关系的图象是( )
A. B.
C. D.
二、填空题
9.如图是一个横断面为抛物线形状的拱桥,当水面在正常水位的情况下,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.则当水位下降m=________时,水面宽为5m?
10.如图,一抛物线形拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位上升1米后,水面的宽度为________米.
11.某桥梁的桥洞可视为抛物线,,最高点C距离水面4m,以AB所在直线为x轴(向右为正向),若以A为原点建立坐标系时,该抛物线的表达式为,已知点D为抛物线上一点,位于点C右侧且距离水面3m,若以点D为原点,以平C行于AB的直线为x轴(向右为正向)建立坐标系时,该物线的表达式为___________.
12.飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是,飞机着陆后滑行_____秒才能停下来.
13.赵州桥的桥拱横截面是近似的抛物线形,其示意图如图所示,其解析式为y=﹣x2.当水面离桥拱顶的高度DO为4m时,水面宽度AB为____m.
14.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=﹣1.2x2+48x,该型号飞机着陆后需滑行_____m才能停下来.
15.某品牌裙子,平均每天可以售出20条,每条盈利40元,经市场调查发现,如果该品牌每条裙子每降价1元,那么平均每天可以多售出2条,那么当裙子降价_________元时,可获得最大利润__________
16.抛出的一小球飞行的高度y与飞行时间x之间满足:,则该小球第2秒时的高度与第_______秒时的高度相同.
三、解答题
17.如图,某中学课外活动小组准备围建一个矩形苗圃园.其中一边靠墙,另外三边用长为20米的篱笆围成.已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.
(1)若这个苗圃园的面积为S平方米,求出S与x之间的函数关系式,并写出自变量x的取值范围;
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大面积.
18.“国庆节期间”某商场销售一款商品,每件的成本是元.销售期间发现:销售单价是元时,每天销售量是件,而销售单价每降低元,每天就可多售出件.但要求销售单价不得低于成本.设当销售单价为元时,每天销售利润为元.
(1)求与之间的函数表达式.
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果每天的销售利润不低于元,那么每天的总成本至少需要 元.
19.某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现:若每箱以50元的价格出售,平均每天销售80箱,价格每提高1元,平均每天少销售2箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
20.为了落实国务院的指示精神,某地方政府出台了一系列“精准扶贫”优惠政策,使贫困户收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量(千克)与销售价(元/千克)有如下关系:.设这种产品每天的销售利润为元.
(1)求与之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克30元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
试卷第3页,共5页
参考答案:
1.D
2.C
3.A
4.C
5.A
6.D
7.D
8.C
9.
10.
11.##
12.
13.20
14.480
15. 15 1250
16.4
17.(1)S=-2x2+20x(1≤x<10)
(2)当矩形苗圃园垂直于墙的边长为5米时,这个苗圃园的面积最大,最大面积为50平方米
18.(1)
(2)元,最大利润元
(3)
19.(1)y=﹣2x+180
(2)w=﹣2x2+260x﹣7200
(3)55元,1050元
20.(1)w=-2x2+120x-1600
(2)销售价定为每千克30元时,每天销售利润最大,最大销售利润200元
(3)每千克25元
答案第1页,共2页
同课章节目录
