1.4图形的中心对称（1）教案

学科
数学
年级
九
时间
总序号
课题
?
1.4图形的中心对称（1）
主备人
授课人
教学目标
和
学习目标
1.经历观察、发现、探究中心对称图形的有关概念和基本性质的过程，积累一定的审美体验。
2.了解中心对称图形及其基本性质，掌握 平行四边形是中心对称图形，会判断一些常见图形是否是中心对称图形。
教学重点
教学难点
?

利用中心对称、对称中心、关于中心对称点的概念解决一些问题．
从一般旋转中导入中心对称．
师
生
互
动
过
程
教学内容和学生活动
教师活动
一、自主学习：
（一）知识准备
1、以合作小组为单位，课前收集一些美丽图案、各种标志、商标等。
2、
轴对称图形。
3、在收集到的图案中，选出是轴对称图形的图案。
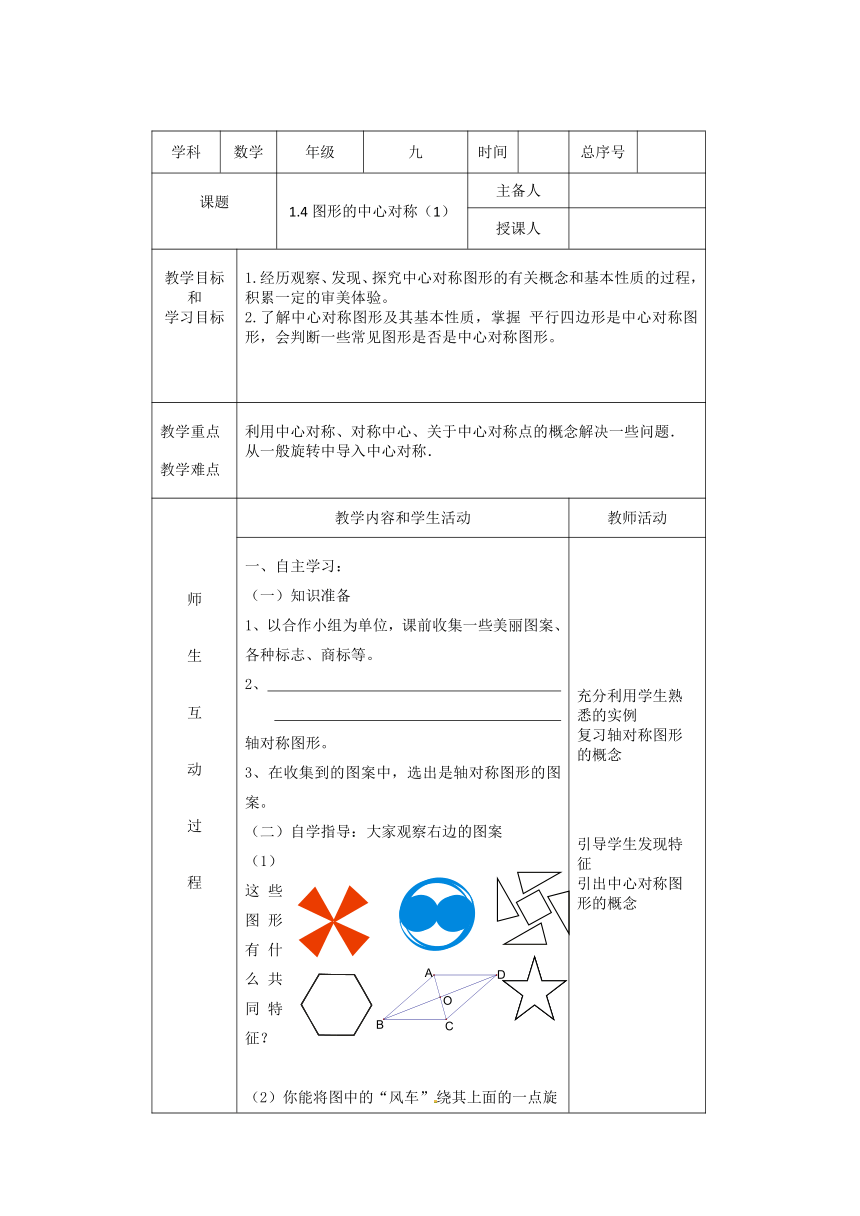
（二）自学指导：大家观察右边的图案
（1）这些图形有什么共同特征？
（2）你能将图中的“风车”绕其上面的一点旋
?
充分利用学生熟悉的实例
复习轴对称图形的概念
引导学生发现特征
引出中心对称图形的概念
师
生
互
动
过
程
教学内容和学生活动
教师活动
?
转180°，使其旋转前后的图形完全重合吗？正六边形呢？
探究活动一：
1、观察电脑演示并思考：
连结对角线AC,BD交点为O，确定原来平行四边形的位置，然后使它绕着点O旋转180°。
（1）此时的平行四边形是否与原来的图形重合？
（2）旋转中心 旋转角是
2、定义：（1）在平面内，一个图形绕 旋转 ，如果旋转前后的图形 ，那么这个图形叫做中心对称图形。这个点叫做它的 。
探究活动二：
1、如图：点A是某个中心对称图形上的一点，绕对称中心0旋转180°后，它变成了点B，点A与点B就是一对 ，且OA=
2、中心对称图形性质：
中心对称图形上的每一对对应点 都 。
3、对比轴对称图形与中心对称图形：
轴对称图形
中心对称图形
有几条对称轴——直线
有一个对称中心——点
沿对称轴对折
绕对称中心旋转180O
对折后与图形两旁的部分重合
旋转后与原图形重合
?
中心对称图形是平面图形（1）旋转180°
（2）能与原来的图形重合
练习
学生回答
填空
引导学生比较轴对称图形与中心对称图形的性质区别
师
生
互
动
过
程
教学内容和学生活动
教师活动
?
探究活动三：
1、线段是中心对称图形吗？ 若是，对称中心是
2、（1）平行四边形是中心对称图形吗？ 它的对称中心是
验证作的结论。
（2）根据上面的验证过程，还可以验证平行四边形的哪些性质？
边：角：对角线：
3 矩形是中心对称图形吗？菱形是中心对称图形吗?
正方形绕两条对角线的交点旋转 度 能与原来的图形重合。
能由此验证正方形的哪些特殊性质？
边：角：对角线：
连接中心对称图形上每一对对称点的线段都经过对称中心，且被
对称中心平分
三、尝试练习：
1、除了平行四边形，正方形，还能找到哪些多边形是中心对称图形？
2、合作探究：下列图形是中心对称图形吗？如果是，找出对称中心。
①正三角形 ②正四边形
③正五边形 ④正六边形
正七边形 正八边形
正九边形 正十边形
总结：边数为偶数的正多边形
边数为奇数的正多边形
3、随堂练习第2题
四、展示反馈：（亮出你的风采！）
在数字0 1 2 3 4 5 6 7 8 9中，哪些是中心对称图形？
五、 回顾总结
1、中心对称图形
2、中心对称图形性质
六、达标检测
正三角形是中心对称图形吗？ 正五角形呢？ 正七角形呢？ ……正四边形呢？ 正六边形呢？ 正八边形呢？ ……边数为 的正多边形都是中心对称图形。
?
引导学生先画出一个平行四边形，让学生通过连接对角线得图，在独立思考的基础上得到结论。引导学生探索与思考
点p与对称中心的线段反向延长，所得射线AB的对应线段CD的交点即为点P′的对称点
任意三角形都不是中心对称图形
引导学生发现中心对称图形的性质
板 书 设 计
1.4图形的中心对称（1）
1、中心对称图形
2、中心对称图形性质
?