北师大版九年级下册3.2圆的对称性课件(共17张PPT)
文档属性
| 名称 | 北师大版九年级下册3.2圆的对称性课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 703.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 07:42:42 | ||
图片预览






文档简介
(共17张PPT)
第二节 圆的对称性
学习目标:
1、理解圆的对称性、圆心角的概念.
2、掌握在同圆或等圆中,圆心角、弦、弧中
有一个量相等就可以推出其他的两个量对
应相等,以及它们在解题中的应用.
O
新课导入
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?
(2)你是用什么办法解决上述问题的?与同伴进行交流.
请同学们观察屏幕上两个半径相等的圆。请回答:
它们能重合吗?如果能重合,请将它们的圆心固定在一起。
O
然后将其中一个圆旋转任意一个角度,这时两个圆还重合吗
O
圆具有旋转不变性,即一个圆绕着它的圆心旋转任意一个角度,都能与原来的圆重合。因此,圆是中心对称圆形,对称中心为圆心。圆的中心对称性是其旋转不变性的特例.
获取新知
知识回顾
1、什么是弦?
2、什么是弧?什么是等弧?
连接圆上任意两点的线段叫做弦。
即:如右图弦AB
.
O
A
B
圆上任意两点间的部分叫作圆弧,简称弧,即:如上图 ;在同圆或等圆中,能够互相重合的弧叫做等弧。
︵
AB
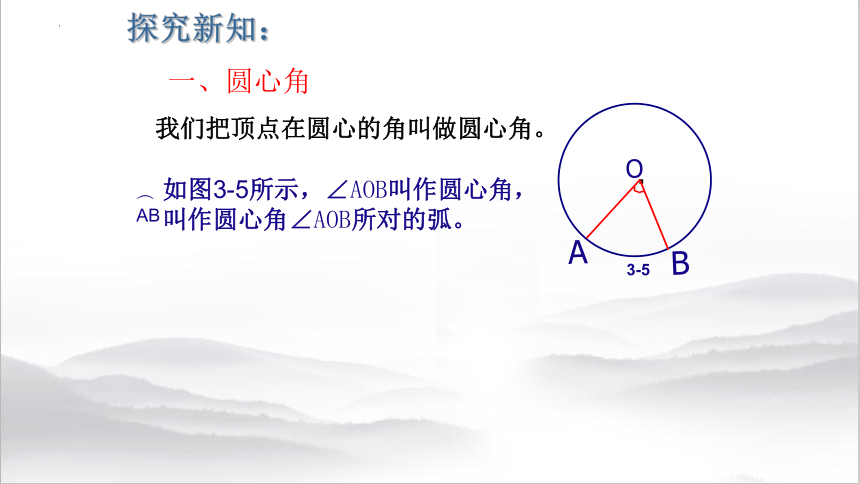
探究新知:
我们把顶点在圆心的角叫做圆心角。
.
O
A
B
3-5
如图3-5所示,∠AOB叫作圆心角, 叫作圆心角∠AOB所对的弧。
︵
AB
一、圆心角
生活中的圆心角
下列各角中,是圆心角的是( )
D
顶点在圆心
.
o
C
D
B
A
.
如图所示圆心角∠AOB=∠COD。 它
︵
CD
︵
AB
们所对的弧 与 相等吗?它们所对的弦
AB与CD相等吗?
弧、弦、圆心角三者关系: (定理)
(B)
(A)
二、弧、弦、圆心角的关系
AB=CD
︵
AB
︵
CD
=
(相等)
在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等。
即:若∠AOB=∠COD,则:
AB=CD
︵
AB
︵
CD
=
⑴在同圆或等圆中,如果弧相等,那么
问题
它们所对的圆心角相等吗?所对的弦相等吗?
.
A
B
.
D
C
O1
O
当 =
︵
AB
︵
CD时
(A)
(B)
AB=CD ∠AOB=∠COD
(相等)
归纳:
在同圆或等圆中,如果两个圆心角、
两条弧、两条弦中有一组量相等,那么它们所对应
的其余各组量也相等。
⑵在同圆或等圆中,如果弦相等,那么它们
所对的圆心角相等吗?所对的弧相等吗?
.
D
C
O1
.
B
A
O
当AB=CD时
(A)
(B)
思考
在同圆或等圆中,如果两条弧相等,那么它们所对
的圆心角 ,所对的弦 。
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 ,所对的弧 。
相等
相等
相等
相等
∠AOB=∠COD,
︵
AB=
︵
CD
(相等)
如图所示,在⊙O中, ,
∠ACB=60°
求证:∠AOB=∠BOC=∠AOC
︵
AB
︵
AC
=
证明:∵
︵
AB
︵
AC
=
∴AB=AC,△ABC是等腰三角形
又∵∠ACB=60°
∴△ABC是等边三角形,AB=BC=CA
( )
∴∠AOB=∠BOC=∠AOC
( )
在同圆中,相等的弧所对的弦相等
在同圆中,相等的弦所对的圆心角相等
例3
随堂练习
⒈下列命题是真命题的是( )
(A)相等的圆心角所对的弧相等
(B)长度相等的两条弧是等弧
(C)等弦所对的圆心角相等
(D)等弧所对的弦相等
⒉如图AB是⊙O的直径, ,∠COD=35°,
求∠AOE的度数。
=
︵
BC
︵
DC
=
︵
DE
D
解:∵
=
︵
BC
︵
DC
=
︵
DE
∴∠BOC=∠COD=∠DOE
∵∠COD=35°
∴∠BOE=3∠COD=3×35°=105°
∴∠AOE=180°-∠BOE=180°-105°
=75°
随堂练习
⒊如图,已知⊙O中,弦AB=CD
求证:AD=BC
证明:∵AB=CD
=
︵
AB
︵
CD
∴
︵
AD
=
即:
︵
BC
∴
︵
AB
︵
BD
-
=
︵
CD
︵
BD
-
∴AD=BC
( )
在同圆中,相等的弦所对的弧相等
( )
在同圆中,相等的弧所对的弦相等
课堂小结:
1、顶点在 的角叫做圆心角。
2、在 中,相等的圆心
角所对的弦 ,所对的弧 。
3、在同圆或等圆中,如果两条弧、两条
弦、两个圆心角中有一组量相等,那么其余
各组量也 。
圆心上
同圆或等圆
相等
相等
相等
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,重足分别为E,F。
C
A
F
B
E
O
D
⑴如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
⑵如果OE=OF那么AB与CD的大小有什么关系?为什么? ∠AOB与∠COD呢?
典例精析
C
弦心距:从圆心到弦的距离。
(如:OC)
O
A
B
相关定义
第二节 圆的对称性
学习目标:
1、理解圆的对称性、圆心角的概念.
2、掌握在同圆或等圆中,圆心角、弦、弧中
有一个量相等就可以推出其他的两个量对
应相等,以及它们在解题中的应用.
O
新课导入
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?
(2)你是用什么办法解决上述问题的?与同伴进行交流.
请同学们观察屏幕上两个半径相等的圆。请回答:
它们能重合吗?如果能重合,请将它们的圆心固定在一起。
O
然后将其中一个圆旋转任意一个角度,这时两个圆还重合吗
O
圆具有旋转不变性,即一个圆绕着它的圆心旋转任意一个角度,都能与原来的圆重合。因此,圆是中心对称圆形,对称中心为圆心。圆的中心对称性是其旋转不变性的特例.
获取新知
知识回顾
1、什么是弦?
2、什么是弧?什么是等弧?
连接圆上任意两点的线段叫做弦。
即:如右图弦AB
.
O
A
B
圆上任意两点间的部分叫作圆弧,简称弧,即:如上图 ;在同圆或等圆中,能够互相重合的弧叫做等弧。
︵
AB
探究新知:
我们把顶点在圆心的角叫做圆心角。
.
O
A
B
3-5
如图3-5所示,∠AOB叫作圆心角, 叫作圆心角∠AOB所对的弧。
︵
AB
一、圆心角
生活中的圆心角
下列各角中,是圆心角的是( )
D
顶点在圆心
.
o
C
D
B
A
.
如图所示圆心角∠AOB=∠COD。 它
︵
CD
︵
AB
们所对的弧 与 相等吗?它们所对的弦
AB与CD相等吗?
弧、弦、圆心角三者关系: (定理)
(B)
(A)
二、弧、弦、圆心角的关系
AB=CD
︵
AB
︵
CD
=
(相等)
在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等。
即:若∠AOB=∠COD,则:
AB=CD
︵
AB
︵
CD
=
⑴在同圆或等圆中,如果弧相等,那么
问题
它们所对的圆心角相等吗?所对的弦相等吗?
.
A
B
.
D
C
O1
O
当 =
︵
AB
︵
CD时
(A)
(B)
AB=CD ∠AOB=∠COD
(相等)
归纳:
在同圆或等圆中,如果两个圆心角、
两条弧、两条弦中有一组量相等,那么它们所对应
的其余各组量也相等。
⑵在同圆或等圆中,如果弦相等,那么它们
所对的圆心角相等吗?所对的弧相等吗?
.
D
C
O1
.
B
A
O
当AB=CD时
(A)
(B)
思考
在同圆或等圆中,如果两条弧相等,那么它们所对
的圆心角 ,所对的弦 。
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 ,所对的弧 。
相等
相等
相等
相等
∠AOB=∠COD,
︵
AB=
︵
CD
(相等)
如图所示,在⊙O中, ,
∠ACB=60°
求证:∠AOB=∠BOC=∠AOC
︵
AB
︵
AC
=
证明:∵
︵
AB
︵
AC
=
∴AB=AC,△ABC是等腰三角形
又∵∠ACB=60°
∴△ABC是等边三角形,AB=BC=CA
( )
∴∠AOB=∠BOC=∠AOC
( )
在同圆中,相等的弧所对的弦相等
在同圆中,相等的弦所对的圆心角相等
例3
随堂练习
⒈下列命题是真命题的是( )
(A)相等的圆心角所对的弧相等
(B)长度相等的两条弧是等弧
(C)等弦所对的圆心角相等
(D)等弧所对的弦相等
⒉如图AB是⊙O的直径, ,∠COD=35°,
求∠AOE的度数。
=
︵
BC
︵
DC
=
︵
DE
D
解:∵
=
︵
BC
︵
DC
=
︵
DE
∴∠BOC=∠COD=∠DOE
∵∠COD=35°
∴∠BOE=3∠COD=3×35°=105°
∴∠AOE=180°-∠BOE=180°-105°
=75°
随堂练习
⒊如图,已知⊙O中,弦AB=CD
求证:AD=BC
证明:∵AB=CD
=
︵
AB
︵
CD
∴
︵
AD
=
即:
︵
BC
∴
︵
AB
︵
BD
-
=
︵
CD
︵
BD
-
∴AD=BC
( )
在同圆中,相等的弦所对的弧相等
( )
在同圆中,相等的弧所对的弦相等
课堂小结:
1、顶点在 的角叫做圆心角。
2、在 中,相等的圆心
角所对的弦 ,所对的弧 。
3、在同圆或等圆中,如果两条弧、两条
弦、两个圆心角中有一组量相等,那么其余
各组量也 。
圆心上
同圆或等圆
相等
相等
相等
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,重足分别为E,F。
C
A
F
B
E
O
D
⑴如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
⑵如果OE=OF那么AB与CD的大小有什么关系?为什么? ∠AOB与∠COD呢?
典例精析
C
弦心距:从圆心到弦的距离。
(如:OC)
O
A
B
相关定义
