北师大版七年级下册5.2 探索轴对称的性质 课件(共18张PPT)
文档属性
| 名称 | 北师大版七年级下册5.2 探索轴对称的性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 638.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 08:04:56 | ||
图片预览



文档简介
(共18张PPT)
5.2 探索轴对称的性质
学习目标:
1、探索及掌握轴对称的性质;
2、会利用轴对称的性质解决实际问题。
重点:掌握轴对称的性质;
难点:探索轴对称的性质以及应用。
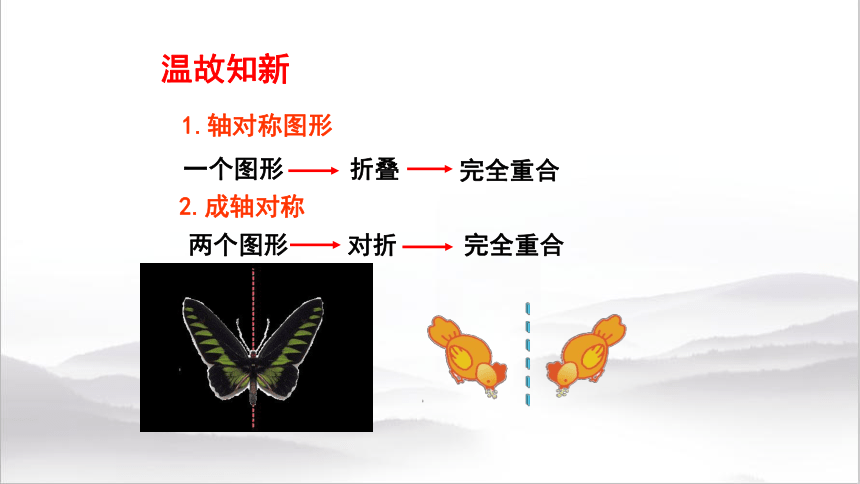
1.轴对称图形
一个图形
2.成轴对称
两个图形
完全重合
折叠
完全重合
对折
温故知新
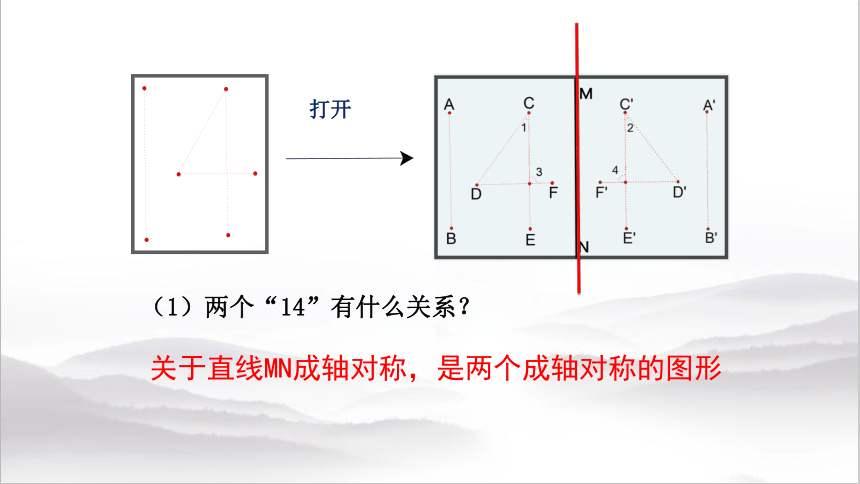
如图:将一张长方形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平,观察并回答以下问题:
知识点一:探索轴对称的性质
(1)两个“14”有什么关系?
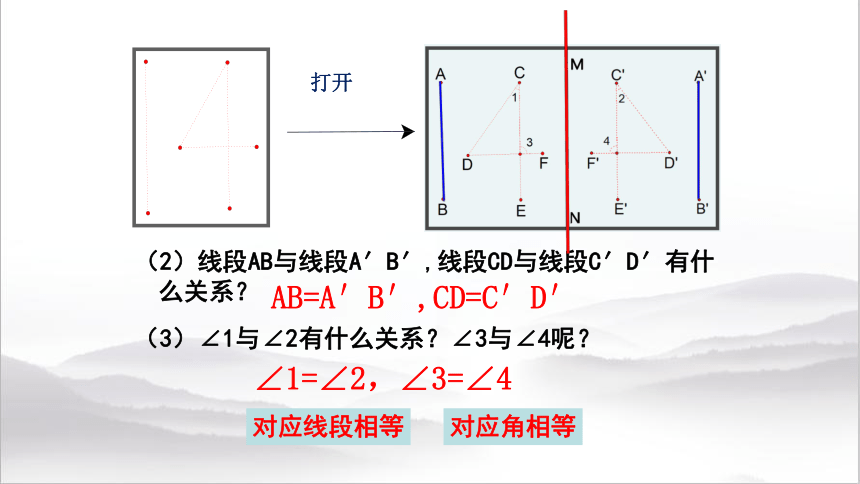
(2)线段AB与线段A′B′,线段CD与线段C′D′有什么关系?
(3)∠1与∠2有什么关系?∠3与∠4呢?
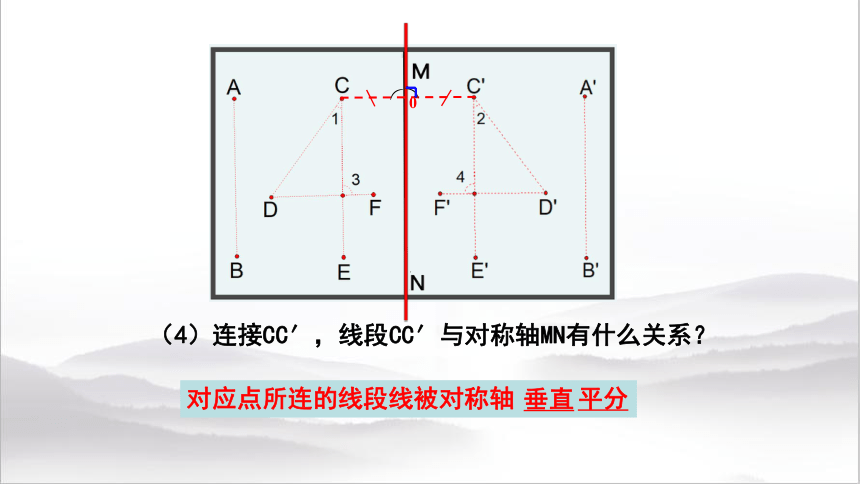
(4)连接CC′,线段CC′与对称轴MN有什么关系?
(1)两个“14”有什么关系?
关于直线MN成轴对称,是两个成轴对称的图形
打开
(2)线段AB与线段A′B′,线段CD与线段C′D′有什么关系?
打开
AB=A′B′,CD=C′D′
对应线段相等
∠1=∠2,∠3=∠4
对应角相等
(3)∠1与∠2有什么关系?∠3与∠4呢?
(4)连接CC′,线段CC′与对称轴MN有什么关系?
对应点所连的线段线被对称轴 平分
︵
︵
垂直
0
下图是一个轴对称图形,则它对称轴是什么?它的对应线段、对应角各有什么关系?对应点所连的线段与对称轴有什么关系?
M
A
A1
B
C
D
D1
C1
B1
3
4
1
2
N
想一想:
在轴对称图形或两个成轴对称的图形中,
2.对应点所连的线段被对称轴垂直平分。
1.对应线段相等,对应角相等;
轴对称的性质
知识点二:轴对称性质的应用
1.画出△ABC关于直线l的对称图形.
知识点二:轴对称性质的应用
2.如图,△ABC与△A1B1C1关于直线l对称,且A1B1=3cm,B1C1=5cm,则BC = cm,∠A1=______,∠C=______,∠B为______.
100°
5
30°
50°
交流研讨
请各个小组在白板上画出已知图形关于直线MN对称的图形.
课堂小结
轴对称的性质
1.对应线段相等,对应角相等
2.对应点所连的线段被对称轴垂直平分
1.如图1是轴对称图形,相等的线段是____________
________,相等的角是__________.
A
B
C
D
E
AB=CD,
BE=CE
∠B=∠C
2.如图2,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴, AB=2cm,AD=3cm,∠ADB=20°,
则(1)BC= cm, CD= cm;∠ADC= °
(2)四边形ABCD的周长为 cm.
B
A
C
D
2
3
10
图1
图2
当堂训练
40
1.已知点A、B直线MN同侧两点,点A1、A关于直线MN对称。连接A1B交直线MN于点P,连接AP。若A1B=5cm,则AP+BP的长为 。
5cm
A
B
P
A1
N
M
拓展提升
2.如图,已知点P是∠AOB内任意一点,点P1,P
关于OA对称,点P2,P关于OB对称.连接P1P2,分
别交OA,OB于C, D.连接PC,PD.若P1P2=10cm,
则△PCD的周长为 .
10cm
.
.
P2
P
.
P1
C
D
B
A
O
拓展提升
谢谢!
5.2 探索轴对称的性质
学习目标:
1、探索及掌握轴对称的性质;
2、会利用轴对称的性质解决实际问题。
重点:掌握轴对称的性质;
难点:探索轴对称的性质以及应用。
1.轴对称图形
一个图形
2.成轴对称
两个图形
完全重合
折叠
完全重合
对折
温故知新
如图:将一张长方形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平,观察并回答以下问题:
知识点一:探索轴对称的性质
(1)两个“14”有什么关系?
(2)线段AB与线段A′B′,线段CD与线段C′D′有什么关系?
(3)∠1与∠2有什么关系?∠3与∠4呢?
(4)连接CC′,线段CC′与对称轴MN有什么关系?
(1)两个“14”有什么关系?
关于直线MN成轴对称,是两个成轴对称的图形
打开
(2)线段AB与线段A′B′,线段CD与线段C′D′有什么关系?
打开
AB=A′B′,CD=C′D′
对应线段相等
∠1=∠2,∠3=∠4
对应角相等
(3)∠1与∠2有什么关系?∠3与∠4呢?
(4)连接CC′,线段CC′与对称轴MN有什么关系?
对应点所连的线段线被对称轴 平分
︵
︵
垂直
0
下图是一个轴对称图形,则它对称轴是什么?它的对应线段、对应角各有什么关系?对应点所连的线段与对称轴有什么关系?
M
A
A1
B
C
D
D1
C1
B1
3
4
1
2
N
想一想:
在轴对称图形或两个成轴对称的图形中,
2.对应点所连的线段被对称轴垂直平分。
1.对应线段相等,对应角相等;
轴对称的性质
知识点二:轴对称性质的应用
1.画出△ABC关于直线l的对称图形.
知识点二:轴对称性质的应用
2.如图,△ABC与△A1B1C1关于直线l对称,且A1B1=3cm,B1C1=5cm,则BC = cm,∠A1=______,∠C=______,∠B为______.
100°
5
30°
50°
交流研讨
请各个小组在白板上画出已知图形关于直线MN对称的图形.
课堂小结
轴对称的性质
1.对应线段相等,对应角相等
2.对应点所连的线段被对称轴垂直平分
1.如图1是轴对称图形,相等的线段是____________
________,相等的角是__________.
A
B
C
D
E
AB=CD,
BE=CE
∠B=∠C
2.如图2,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴, AB=2cm,AD=3cm,∠ADB=20°,
则(1)BC= cm, CD= cm;∠ADC= °
(2)四边形ABCD的周长为 cm.
B
A
C
D
2
3
10
图1
图2
当堂训练
40
1.已知点A、B直线MN同侧两点,点A1、A关于直线MN对称。连接A1B交直线MN于点P,连接AP。若A1B=5cm,则AP+BP的长为 。
5cm
A
B
P
A1
N
M
拓展提升
2.如图,已知点P是∠AOB内任意一点,点P1,P
关于OA对称,点P2,P关于OB对称.连接P1P2,分
别交OA,OB于C, D.连接PC,PD.若P1P2=10cm,
则△PCD的周长为 .
10cm
.
.
P2
P
.
P1
C
D
B
A
O
拓展提升
谢谢!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
