人教版九年级数学上册 第二十一章 一元二次方程 单元过关练习 (Word版,含答案)
文档属性
| 名称 | 人教版九年级数学上册 第二十一章 一元二次方程 单元过关练习 (Word版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 32.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 00:00:00 | ||
图片预览


文档简介
二十一章一元二次方程单元过关练习-数学九年级上册人教版
一、单选题
1.下列方程中,是关于x的一元二次方程的为( )
A. B.x2-x-1=0 C. D.
2.若x=1是方程x2﹣4x+m=0的根,则m的值为( )
A.﹣3 B.﹣5 C.3 D.5
3.已知关于x的方程,则下列关于该方程根的判断,正确的是( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.不能确定
4.一元二次方程x2﹣8x+5=0配方后可化为( )
A.(x﹣4)=19 B.(x+4)=﹣19
C.(x﹣4)2=11 D.(x+4)2=16
5.若方程的一个根为,则k的值是( )
A.7 B. C.4 D.
6.已知关于x的一元二次方程总有两个不相等的实数根,则m的取值范围是( )
A. B. C.且 D.
7.演讲比赛前,每个同学都与其他同学握手一次,表示问好,如果有x名同学参加演讲,握手总次数为435次,根据题意,求人数x可列出方程为( )
A.x (x-1) =435 B.x (x+1) =435
C.2x (x+1) =435 D.
8.有支球队参加篮球比赛,共比赛66场,每两队之间都比赛一场,则下列方程中正确的是( )
A. x(x-1)=66 B. x(x+1)=66
C.x(x-1)=66 D.x(x+1)=66
二、填空题
9.一元二次方程的解为 .
10.若关于x的一元二次方程 有一个根为1,则方程另一个根为 .
11.一元二次方程的两根为,,则 .
12.已知m是关于x的方程x2﹣3x﹣4=0的一个根,则3m2﹣9m﹣2= .
13.如果关于x的一元二次方程 有两个不相等的实数根,则m的取值范围是 .
14.抛物线y=2x2-3x-1与坐标轴的交点个数为 .
15.一个小球以 速度开始向前滚动,并且均匀减速, 后小球停止滚动.小球滚动 约用了 秒(结果保留小数点后一位)
16.教师节期间,我校九年级组教师向本组其他教师各发一条祝福短信.据统计,全组共发了90条祝福短信.如果设九年级组共有 名教师,依题意可列出的方程是 .
三、解答题
17.解方程
(1)
(2)
(3)
(4)
18.阅读例题,解答下题.
范例:解方程:x2+∣x+1∣﹣1=0
解:⑴当x+1≥0,即x≥﹣1时,
x2+x+1﹣1=0
x2+x=0
解得x1=0,x2=﹣1
⑵当x+1<0,即x<﹣1时,
x2﹣(x+1)﹣1=0
x2﹣x﹣2=0
解得x1=﹣1,x2=2
∵x<﹣1,∴x1=﹣1,x2=2都舍去.
综上所述,原方程的解是x1=0,x2=﹣1
依照上例解法,解方程:x2﹣2∣x-2∣-4=0
19.关于x的方程x2﹣(k+1)x+k=0有两个相等的实数根,求k的值.
20.已知关于x的一元二次方程ax2+bx+1=0(a≠0)有两个相等的实数根,求 的值.
21.在△ABC中,BC=2,AB=2 ,AC=b,且关于x的方程x2﹣4x+b=0有两个相等的实数根,求AC边上的中线长及∠A的度数.
22.已知抛物线 .求证:无论k为何值,该二次函数的图象与x轴都有交点.
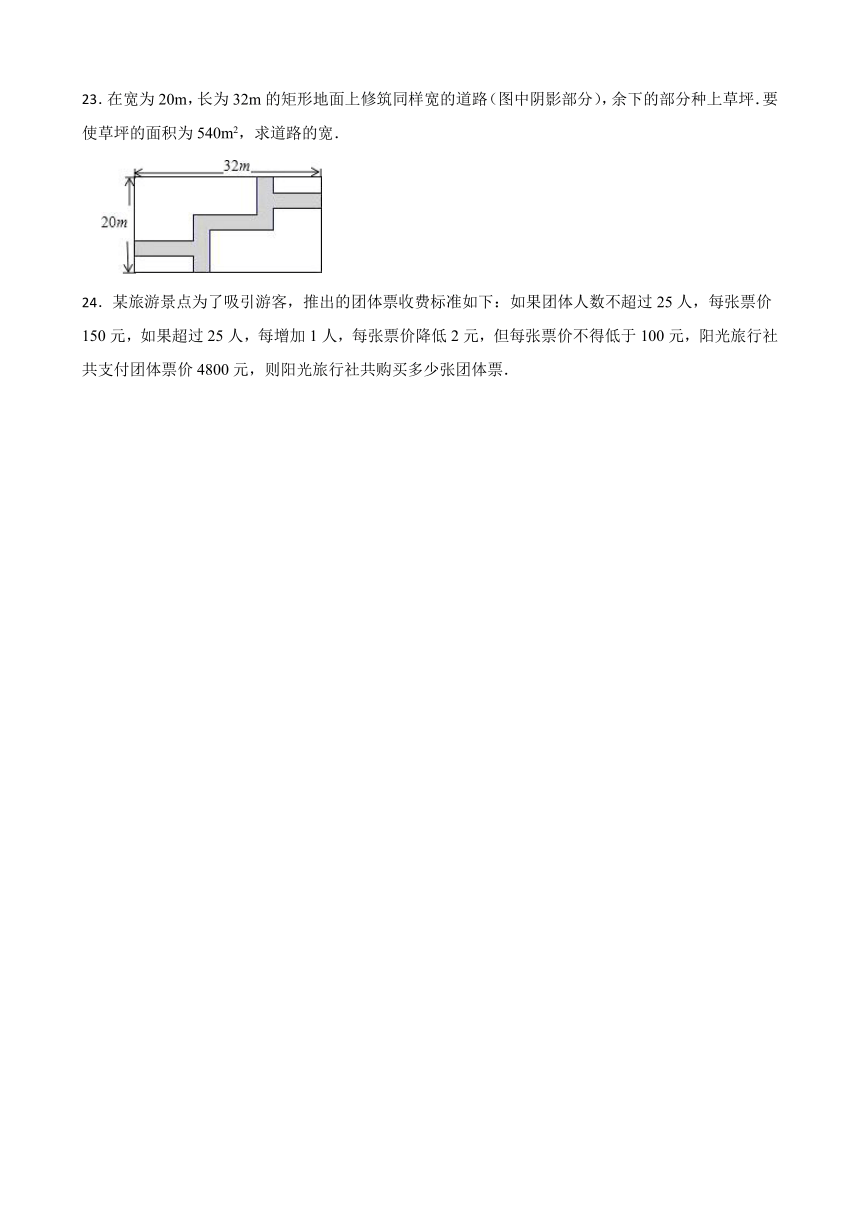
23.在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
24.某旅游景点为了吸引游客,推出的团体票收费标准如下:如果团体人数不超过25人,每张票价150元,如果超过25人,每增加1人,每张票价降低2元,但每张票价不得低于100元,阳光旅行社共支付团体票价4800元,则阳光旅行社共购买多少张团体票.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】A
9.【答案】,
10.【答案】2
11.【答案】1
12.【答案】10
13.【答案】m<2且m≠1
14.【答案】3
15.【答案】1.2
16.【答案】x2-x-90=0
17.【答案】(1)∵ ,
∴ ,
∴ ,
∴ ,
(2) ,
∴ ,
∴ ,
∴ ,
(3)
方程整理得: ,
∵a=3,b=-2,c=-6,
∴△=4+72=76>0,
∴ ,
∴ ,
(4)
移项得: ,
因式分解得: ,
∴x-2=0或3x+2=0,
∴ , .
18.【答案】(1)当x﹣2≥0,即x≥2时,
x2﹣2(x﹣2)﹣4=0
x2-2x=0
解得x1=0,x2=2
∵x≥2,∴x1=0 舍去
⑵当x﹣2<0,即x<2时,
x2+2(x﹣2)﹣4=0
x2+2x﹣8=0
解得x1=﹣4 ,x2=2
∵x<2,∴x2=2舍去.
综上所述,原方程的解是x1=2,x2=﹣4.
19.【答案】解:∵关于x的方程有两个相等的实数根,
∴,
∴,
∴,
解得.
20.【答案】解:∵方程ax2+bx+1=0(a≠0)有两个相等的实数根,
∴b2-4a=0,∴b2=4a,
将b2=4a代入
= ,
=
=
=4.
21.【答案】解:∵一元二次方程x2﹣4x+b=0有两个相等的实数根,
∴b2﹣4ac=0,即(﹣4)2﹣4b=0,
∴b=4.
∴AC=4,
∴AB2+BC2=AC2,
∵△ABC为直角三角形,
∵直角三角形斜边上的中线等于斜边的一半,
∴AC边上的中线长=2,
∵AC=4,
∴∠A=30°.
22.【答案】解:令y=0, ,
∵ ,
,
∴二次函数的图象与x轴都有交点.
23.【答案】解:设道路的宽为xm,根据题意得:
(32﹣x)(20﹣x)=540,
解得:x1=2,x2=50(不合题意,舍去),
答:道路的宽是2m.
24.【答案】解:∵150×25=3750<4800,∴购买的团体票超过25张,设共购买了x张团体票,由题意列方程得x×[150﹣2(x﹣25)]=4800,x2﹣100x+2400=0,解得x1=60,x2=40,当x1=60时,超过25人的人数为35人,票价降70元,降价后为150﹣70=80元<100元,不符题意,舍去,x2=40符合题意,∴x=40,答:共购买了40张团体票
一、单选题
1.下列方程中,是关于x的一元二次方程的为( )
A. B.x2-x-1=0 C. D.
2.若x=1是方程x2﹣4x+m=0的根,则m的值为( )
A.﹣3 B.﹣5 C.3 D.5
3.已知关于x的方程,则下列关于该方程根的判断,正确的是( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.不能确定
4.一元二次方程x2﹣8x+5=0配方后可化为( )
A.(x﹣4)=19 B.(x+4)=﹣19
C.(x﹣4)2=11 D.(x+4)2=16
5.若方程的一个根为,则k的值是( )
A.7 B. C.4 D.
6.已知关于x的一元二次方程总有两个不相等的实数根,则m的取值范围是( )
A. B. C.且 D.
7.演讲比赛前,每个同学都与其他同学握手一次,表示问好,如果有x名同学参加演讲,握手总次数为435次,根据题意,求人数x可列出方程为( )
A.x (x-1) =435 B.x (x+1) =435
C.2x (x+1) =435 D.
8.有支球队参加篮球比赛,共比赛66场,每两队之间都比赛一场,则下列方程中正确的是( )
A. x(x-1)=66 B. x(x+1)=66
C.x(x-1)=66 D.x(x+1)=66
二、填空题
9.一元二次方程的解为 .
10.若关于x的一元二次方程 有一个根为1,则方程另一个根为 .
11.一元二次方程的两根为,,则 .
12.已知m是关于x的方程x2﹣3x﹣4=0的一个根,则3m2﹣9m﹣2= .
13.如果关于x的一元二次方程 有两个不相等的实数根,则m的取值范围是 .
14.抛物线y=2x2-3x-1与坐标轴的交点个数为 .
15.一个小球以 速度开始向前滚动,并且均匀减速, 后小球停止滚动.小球滚动 约用了 秒(结果保留小数点后一位)
16.教师节期间,我校九年级组教师向本组其他教师各发一条祝福短信.据统计,全组共发了90条祝福短信.如果设九年级组共有 名教师,依题意可列出的方程是 .
三、解答题
17.解方程
(1)
(2)
(3)
(4)
18.阅读例题,解答下题.
范例:解方程:x2+∣x+1∣﹣1=0
解:⑴当x+1≥0,即x≥﹣1时,
x2+x+1﹣1=0
x2+x=0
解得x1=0,x2=﹣1
⑵当x+1<0,即x<﹣1时,
x2﹣(x+1)﹣1=0
x2﹣x﹣2=0
解得x1=﹣1,x2=2
∵x<﹣1,∴x1=﹣1,x2=2都舍去.
综上所述,原方程的解是x1=0,x2=﹣1
依照上例解法,解方程:x2﹣2∣x-2∣-4=0
19.关于x的方程x2﹣(k+1)x+k=0有两个相等的实数根,求k的值.
20.已知关于x的一元二次方程ax2+bx+1=0(a≠0)有两个相等的实数根,求 的值.
21.在△ABC中,BC=2,AB=2 ,AC=b,且关于x的方程x2﹣4x+b=0有两个相等的实数根,求AC边上的中线长及∠A的度数.
22.已知抛物线 .求证:无论k为何值,该二次函数的图象与x轴都有交点.
23.在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
24.某旅游景点为了吸引游客,推出的团体票收费标准如下:如果团体人数不超过25人,每张票价150元,如果超过25人,每增加1人,每张票价降低2元,但每张票价不得低于100元,阳光旅行社共支付团体票价4800元,则阳光旅行社共购买多少张团体票.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】A
9.【答案】,
10.【答案】2
11.【答案】1
12.【答案】10
13.【答案】m<2且m≠1
14.【答案】3
15.【答案】1.2
16.【答案】x2-x-90=0
17.【答案】(1)∵ ,
∴ ,
∴ ,
∴ ,
(2) ,
∴ ,
∴ ,
∴ ,
(3)
方程整理得: ,
∵a=3,b=-2,c=-6,
∴△=4+72=76>0,
∴ ,
∴ ,
(4)
移项得: ,
因式分解得: ,
∴x-2=0或3x+2=0,
∴ , .
18.【答案】(1)当x﹣2≥0,即x≥2时,
x2﹣2(x﹣2)﹣4=0
x2-2x=0
解得x1=0,x2=2
∵x≥2,∴x1=0 舍去
⑵当x﹣2<0,即x<2时,
x2+2(x﹣2)﹣4=0
x2+2x﹣8=0
解得x1=﹣4 ,x2=2
∵x<2,∴x2=2舍去.
综上所述,原方程的解是x1=2,x2=﹣4.
19.【答案】解:∵关于x的方程有两个相等的实数根,
∴,
∴,
∴,
解得.
20.【答案】解:∵方程ax2+bx+1=0(a≠0)有两个相等的实数根,
∴b2-4a=0,∴b2=4a,
将b2=4a代入
= ,
=
=
=4.
21.【答案】解:∵一元二次方程x2﹣4x+b=0有两个相等的实数根,
∴b2﹣4ac=0,即(﹣4)2﹣4b=0,
∴b=4.
∴AC=4,
∴AB2+BC2=AC2,
∵△ABC为直角三角形,
∵直角三角形斜边上的中线等于斜边的一半,
∴AC边上的中线长=2,
∵AC=4,
∴∠A=30°.
22.【答案】解:令y=0, ,
∵ ,
,
∴二次函数的图象与x轴都有交点.
23.【答案】解:设道路的宽为xm,根据题意得:
(32﹣x)(20﹣x)=540,
解得:x1=2,x2=50(不合题意,舍去),
答:道路的宽是2m.
24.【答案】解:∵150×25=3750<4800,∴购买的团体票超过25张,设共购买了x张团体票,由题意列方程得x×[150﹣2(x﹣25)]=4800,x2﹣100x+2400=0,解得x1=60,x2=40,当x1=60时,超过25人的人数为35人,票价降70元,降价后为150﹣70=80元<100元,不符题意,舍去,x2=40符合题意,∴x=40,答:共购买了40张团体票
同课章节目录
