1.4.1 第1课时 有理数的乘法法则 课件(共21张PPT)
文档属性
| 名称 | 1.4.1 第1课时 有理数的乘法法则 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 944.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
1.4.1 第1课时
有理数的乘法法则
人教版 七年级上册
教学目标
教学目标:
1.理解有理数乘法的意义,掌握有理数乘法法则.
2.能准确地进行有理数的乘法运算,培养学生的探索能力.
3.传授知识的同时,注意培养学生勇于探索新知的精神.
重点:有理数的乘法法则.
难点:有理数乘法中的符号法则.
新知导入
1.计算:
(1)(-5)+(-5)= ;
(2)(-5)+(-5)+(-5)= ;
(3)(-5)+(-5)+(-5)+(-5)= ;
(4)(-5)+(-5)+(-5)+(-5)+(-5)= .
-10
-15
-20
-25
2.猜想下列各式的值:
(-5)×2= ;(-5)×3= ;
(-5)×4= ;(-5)×5= .
-10
-15
-20
-25
3.两个有理数相乘有几种情况?
五种:
正数乘正数;负数乘负数;正数乘负数;
正数乘0;负数乘0.
新知讲解
3 × 3 = 9,
3 × 2 = 6,
3 × 1 = 3 ,
3 × 0 = 0
观察下面的乘法算式,你能发现什么规律吗
要使这个规律在引入负数后仍成立,那么应有
3×(-1)= -3,
3×(-2)= ,
3×(-3)= .
-6
-9
前一乘数相同
随着第二个乘数逐次递减1,积逐次递减 3 .
当第二个乘数从 -1 减小为 2时,
积从 减小为 .
-3
-6
当第二个乘数从 0 减小为 1时,
积从 减小为 .
0
-3
新知讲解
3 × 3 =
2 × 3 =
1 × 3 =
0 × 3 =
( 1) ×3= ,
( 2)×3 = ,
( 3)×3 = ,
( 4)×3 = .
随着第一个乘数逐次递减1,积逐次递减 3 .
3
6
9
观察下面的乘法算式,你又能发现什么规律
要使这个规律在引入负数后仍然成立,那么应有:
9
6
3
0
12
后一乘数相同
新知讲解
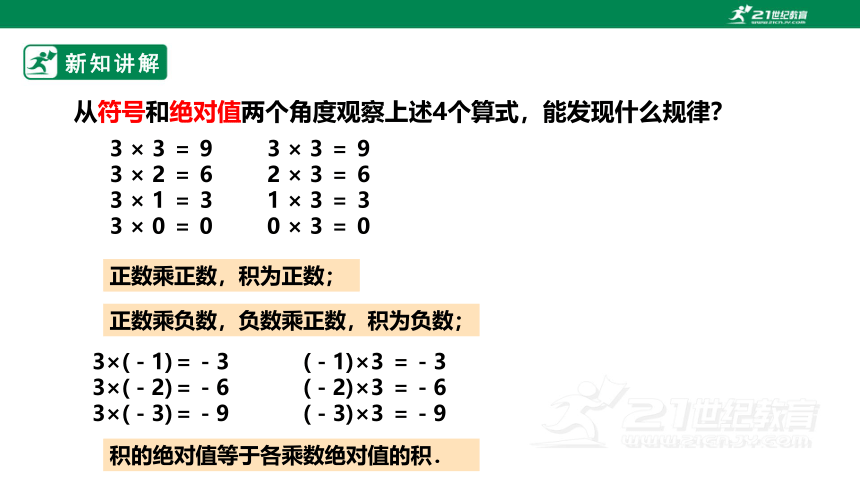
从符号和绝对值两个角度观察上述4个算式,能发现什么规律?
3 × 3 = 9
2 × 3 = 6
1 × 3 = 3
0 × 3 = 0
3 × 3 = 9
3 × 2 = 6
3 × 1 = 3
3 × 0 = 0
3×(-1)=-3
3×(-2)=-6
3×(-3)=-9
(-1)×3 =-3
(-2)×3 =-6
(-3)×3 =-9
积的绝对值等于各乘数绝对值的积.
正数乘正数,积为正数;
正数乘负数,负数乘正数,积为负数;
新知讲解
( 3) × 3 =
( 3) × 2 =
( 3) × 1 =
( 3) × 0 =
( 3)×( 1) = ,
( 3)×( 2) = ,
( 3)×( 3) = ,
( 3)×( 4) = .
随着第二个乘数逐次递减1,积逐次递增 3 .
3
6
9
要使这个规律在引入负数后仍然成立,那么应有:
9
6
3
0
12
利用上面的结论计算下面算式,你发现有什么规律
结论:负数乘负数,积为正数,
积的绝对值等于各乘数绝对值的积.
新知讲解
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
新知讲解
怎样利用法则来进行两有理数的乘法运算与得出结果?
=-28
所以
( 7)×4
, ………… …………________________
把绝对值相乘
7×4=28
=10.
(2)
……………………… _______________
=-( ),……_____________
异号两数相乘
得负
( 5)×( 2)
( 7)×4
( 7)×4
所以
……………得正
, …………………把绝对值相乘
5×2=10
=+( )
……………………同号两数相乘
(1)
( 5)×( 2)
( 5)×( 2)
归纳总结
有理数乘法的运算步骤
★第一步:先观察是否有0因数;
★第二步:确定积的符号;
★第三步:确定积的绝对值.
新知讲解
(2)8×(-1)=-(8×1)=-8.
解:(1)(-3)×9=-(3×9)=-27.
(1)(-3)×9;(2)8×(-1);
例1 计算:
(3)( )×(-2)=+( ×2 )=1.
(3)( )×(-2).
从(2)中可以看出,
要得到一个数的相反数,只要将它乘-1
(3)中两个数的乘积是1,我们说这两个数互为倒数
结论:乘积是1的两个数互为倒数
新知讲解
例2 用正负数表示气温的变化量,上升为正,下降为负.
登山队攀登一座山峰,每登高1 km气温的变化量为-6℃,攀登3 km后,气温有什么变化?
解:(-6)×3=18(℃)
答:气温下降18℃.
课堂练习
1. 计算-4×的值是( )
A.- B.
C.-10 D.10
D
2. 下列各组数中,互为倒数的是( )
A.2与-|-2| B.-(+2)与
C.-(-2)与- D.-与+(-2)
D
课堂练习
3. 若三个数a,b,c满足(a-b)(b-c)>0, 则下列关于a,b,c 三个数的大小关系叙述正确的是( )
可以确定最大的数是a,最小的数是c
可以确定最大的数是c,最小的数是a
可以确定中间的一个数是b
无法确定它们的大小关系
C
课堂练习
4.若a,b是两个有理数,且ab>0,a+b<0,则 ( )
A.a<0,b>0 B.a<0,b<0
C.a>0,b>0 D.a>0,b<0
B
5.已知有理数m,n在数轴上的对应点的位置如图所示,则下列判断正确的是( )
A.m>0 B.n<0 C.mn<0 D.m-n>0
C
课堂练习
6. 计算:
(1)(-3)×(-24);
(2)(-1000)×0.1;
(3)(-12.5)×(-0.8);
(4)×.
解:原式=3×24=72;
原式=-1000×0.1=-100;
原式=12.5×0.8=10;
原式=-×=-2
课堂练习
7.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:
(-5)×60=-300
答:销售额减少了300元.
课堂练习
∵ |a|=3,|b|=4,
∴a=±3,b=±4.
∵a+b<0,
∴a=±3,b=-4,
∴ab=3×(-4)=-12
或ab=(-3)×(-4)=12
∴ ab的值是±12.
8.已知|a|=3,|b|=4,且a+b<0,求ab的值.
解:
课堂总结
有理数的乘法
倒数
两个数相乘
同号得正
异号得负
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.4.1 第1课时
有理数的乘法法则
人教版 七年级上册
教学目标
教学目标:
1.理解有理数乘法的意义,掌握有理数乘法法则.
2.能准确地进行有理数的乘法运算,培养学生的探索能力.
3.传授知识的同时,注意培养学生勇于探索新知的精神.
重点:有理数的乘法法则.
难点:有理数乘法中的符号法则.
新知导入
1.计算:
(1)(-5)+(-5)= ;
(2)(-5)+(-5)+(-5)= ;
(3)(-5)+(-5)+(-5)+(-5)= ;
(4)(-5)+(-5)+(-5)+(-5)+(-5)= .
-10
-15
-20
-25
2.猜想下列各式的值:
(-5)×2= ;(-5)×3= ;
(-5)×4= ;(-5)×5= .
-10
-15
-20
-25
3.两个有理数相乘有几种情况?
五种:
正数乘正数;负数乘负数;正数乘负数;
正数乘0;负数乘0.
新知讲解
3 × 3 = 9,
3 × 2 = 6,
3 × 1 = 3 ,
3 × 0 = 0
观察下面的乘法算式,你能发现什么规律吗
要使这个规律在引入负数后仍成立,那么应有
3×(-1)= -3,
3×(-2)= ,
3×(-3)= .
-6
-9
前一乘数相同
随着第二个乘数逐次递减1,积逐次递减 3 .
当第二个乘数从 -1 减小为 2时,
积从 减小为 .
-3
-6
当第二个乘数从 0 减小为 1时,
积从 减小为 .
0
-3
新知讲解
3 × 3 =
2 × 3 =
1 × 3 =
0 × 3 =
( 1) ×3= ,
( 2)×3 = ,
( 3)×3 = ,
( 4)×3 = .
随着第一个乘数逐次递减1,积逐次递减 3 .
3
6
9
观察下面的乘法算式,你又能发现什么规律
要使这个规律在引入负数后仍然成立,那么应有:
9
6
3
0
12
后一乘数相同
新知讲解
从符号和绝对值两个角度观察上述4个算式,能发现什么规律?
3 × 3 = 9
2 × 3 = 6
1 × 3 = 3
0 × 3 = 0
3 × 3 = 9
3 × 2 = 6
3 × 1 = 3
3 × 0 = 0
3×(-1)=-3
3×(-2)=-6
3×(-3)=-9
(-1)×3 =-3
(-2)×3 =-6
(-3)×3 =-9
积的绝对值等于各乘数绝对值的积.
正数乘正数,积为正数;
正数乘负数,负数乘正数,积为负数;
新知讲解
( 3) × 3 =
( 3) × 2 =
( 3) × 1 =
( 3) × 0 =
( 3)×( 1) = ,
( 3)×( 2) = ,
( 3)×( 3) = ,
( 3)×( 4) = .
随着第二个乘数逐次递减1,积逐次递增 3 .
3
6
9
要使这个规律在引入负数后仍然成立,那么应有:
9
6
3
0
12
利用上面的结论计算下面算式,你发现有什么规律
结论:负数乘负数,积为正数,
积的绝对值等于各乘数绝对值的积.
新知讲解
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
新知讲解
怎样利用法则来进行两有理数的乘法运算与得出结果?
=-28
所以
( 7)×4
, ………… …………________________
把绝对值相乘
7×4=28
=10.
(2)
……………………… _______________
=-( ),……_____________
异号两数相乘
得负
( 5)×( 2)
( 7)×4
( 7)×4
所以
……………得正
, …………………把绝对值相乘
5×2=10
=+( )
……………………同号两数相乘
(1)
( 5)×( 2)
( 5)×( 2)
归纳总结
有理数乘法的运算步骤
★第一步:先观察是否有0因数;
★第二步:确定积的符号;
★第三步:确定积的绝对值.
新知讲解
(2)8×(-1)=-(8×1)=-8.
解:(1)(-3)×9=-(3×9)=-27.
(1)(-3)×9;(2)8×(-1);
例1 计算:
(3)( )×(-2)=+( ×2 )=1.
(3)( )×(-2).
从(2)中可以看出,
要得到一个数的相反数,只要将它乘-1
(3)中两个数的乘积是1,我们说这两个数互为倒数
结论:乘积是1的两个数互为倒数
新知讲解
例2 用正负数表示气温的变化量,上升为正,下降为负.
登山队攀登一座山峰,每登高1 km气温的变化量为-6℃,攀登3 km后,气温有什么变化?
解:(-6)×3=18(℃)
答:气温下降18℃.
课堂练习
1. 计算-4×的值是( )
A.- B.
C.-10 D.10
D
2. 下列各组数中,互为倒数的是( )
A.2与-|-2| B.-(+2)与
C.-(-2)与- D.-与+(-2)
D
课堂练习
3. 若三个数a,b,c满足(a-b)(b-c)>0, 则下列关于a,b,c 三个数的大小关系叙述正确的是( )
可以确定最大的数是a,最小的数是c
可以确定最大的数是c,最小的数是a
可以确定中间的一个数是b
无法确定它们的大小关系
C
课堂练习
4.若a,b是两个有理数,且ab>0,a+b<0,则 ( )
A.a<0,b>0 B.a<0,b<0
C.a>0,b>0 D.a>0,b<0
B
5.已知有理数m,n在数轴上的对应点的位置如图所示,则下列判断正确的是( )
A.m>0 B.n<0 C.mn<0 D.m-n>0
C
课堂练习
6. 计算:
(1)(-3)×(-24);
(2)(-1000)×0.1;
(3)(-12.5)×(-0.8);
(4)×.
解:原式=3×24=72;
原式=-1000×0.1=-100;
原式=12.5×0.8=10;
原式=-×=-2
课堂练习
7.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:
(-5)×60=-300
答:销售额减少了300元.
课堂练习
∵ |a|=3,|b|=4,
∴a=±3,b=±4.
∵a+b<0,
∴a=±3,b=-4,
∴ab=3×(-4)=-12
或ab=(-3)×(-4)=12
∴ ab的值是±12.
8.已知|a|=3,|b|=4,且a+b<0,求ab的值.
解:
课堂总结
有理数的乘法
倒数
两个数相乘
同号得正
异号得负
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
