12.1 全等三角形 课件(共32张PPT)
文档属性
| 名称 | 12.1 全等三角形 课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 00:00:00 | ||
图片预览



文档简介
(共32张PPT)
人教版 八年级上册
12.1 全等三角形
学习目标
1.理解并掌握全等三角形的概念及其基本性质.(重点)
2.能找准全等三角形的对应边,理解全等三角形的对应角相等.(难点)
3.能进行简单的推理和计算,并解决一些实际问题.(难点)
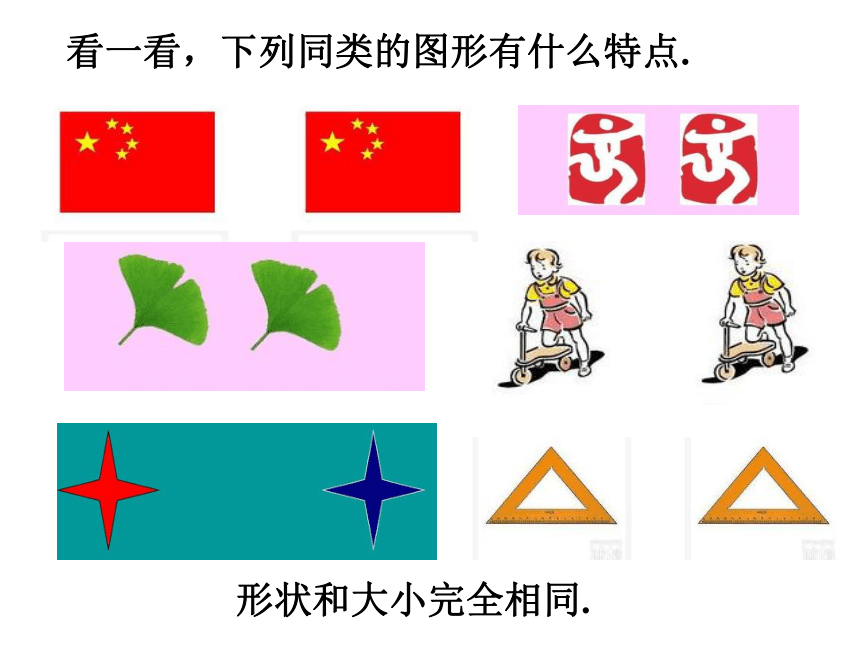
看一看,下列同类的图形有什么特点.
形状和大小完全相同.
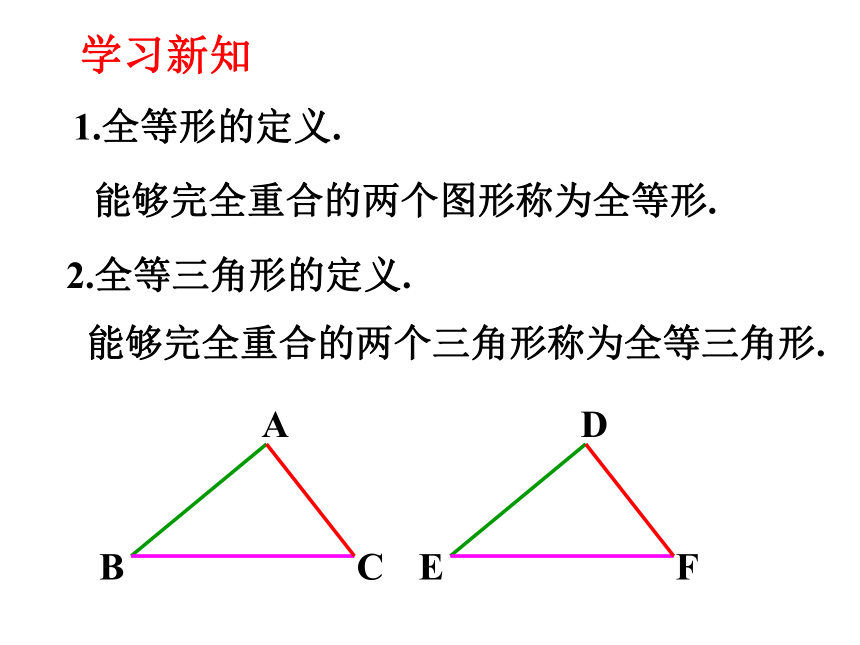
能够完全重合的两个图形称为全等形.
1.全等形的定义.
能够完全重合的两个三角形称为全等三角形.
2.全等三角形的定义.
A
B
C
D
E
F
学习新知
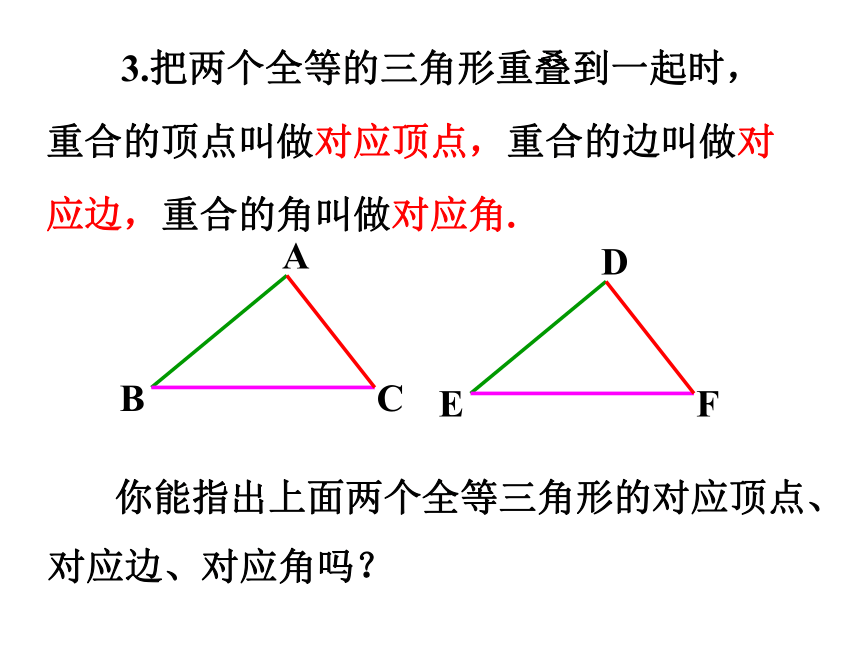
3.把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
你能指出上面两个全等三角形的对应顶点、
对应边、对应角吗?
A
B
C
D
E
F
N
M
S
O
T
D
C
O
A
B
A
B
C
D
E
F
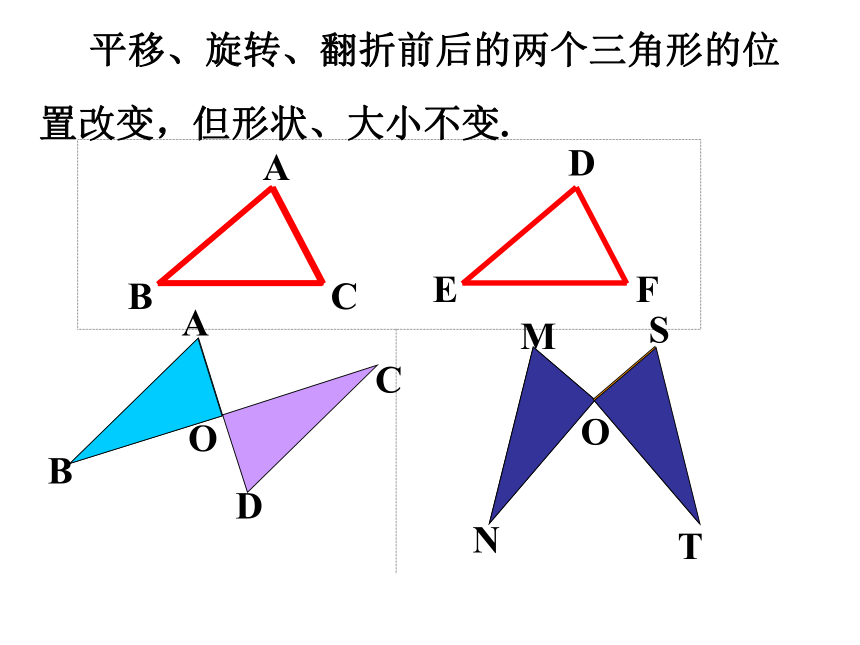
平移、旋转、翻折前后的两个三角形的位置改变,但形状、大小不变.
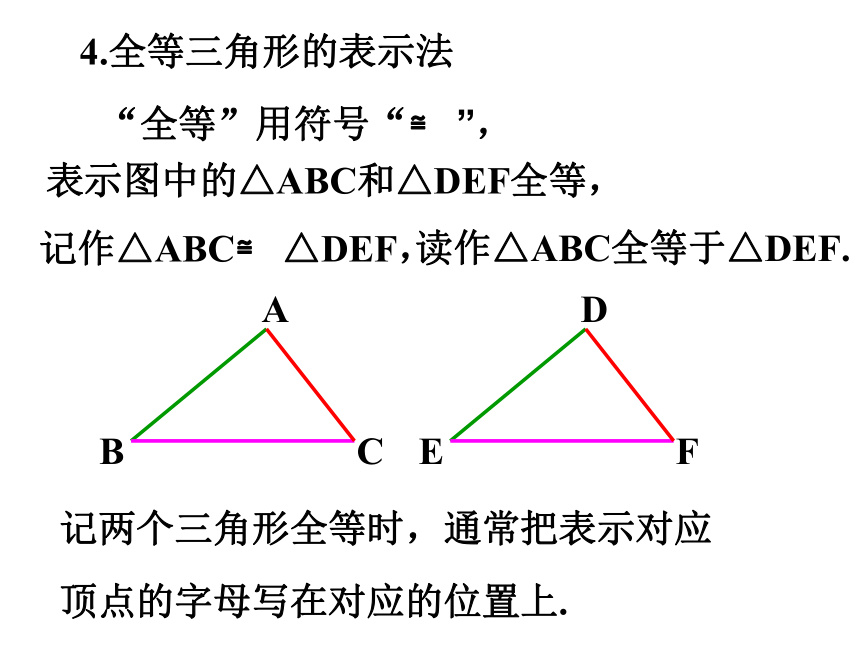
“全等”用符号“≌ ”,
4.全等三角形的表示法
记作△ABC≌ △DEF,
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
A
B
C
D
E
F
读作△ABC全等于△DEF.
表示图中的△ABC和△DEF全等,
N
M
S
O
T
D
C
O
A
B
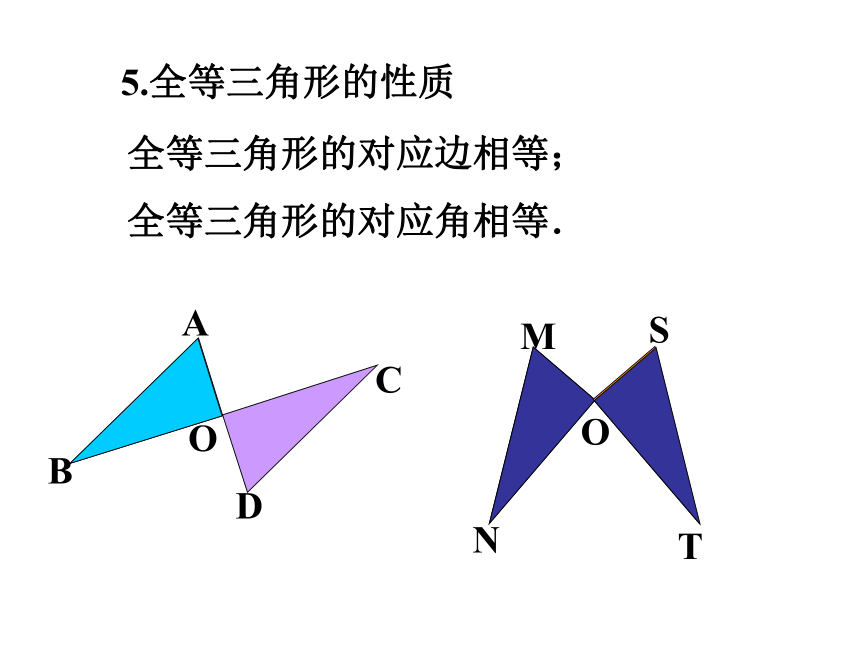
全等三角形的对应边相等;
5.全等三角形的性质
全等三角形的对应角相等.
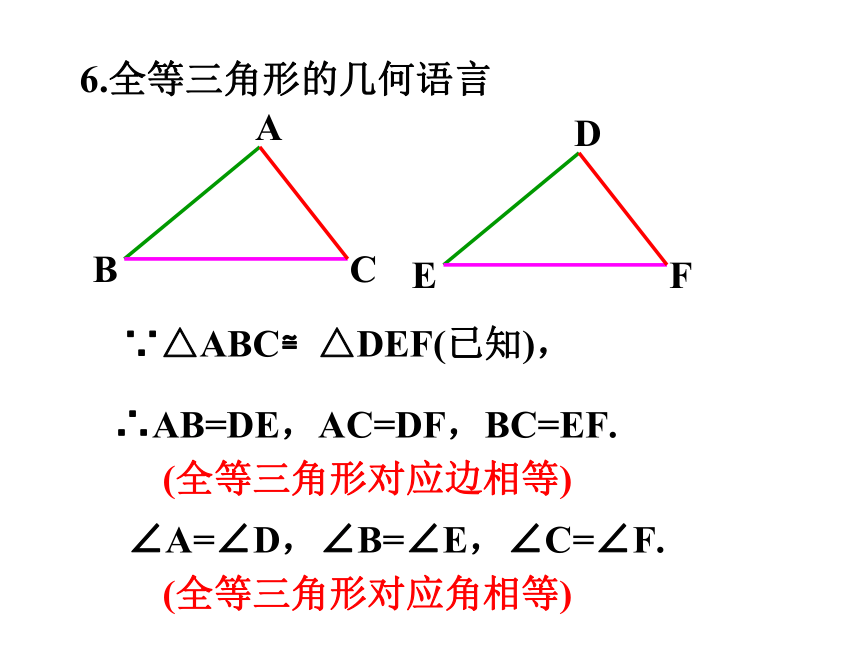
6.全等三角形的几何语言
∵△ABC≌△DEF(已知),
∴AB=DE,AC=DF,BC=EF.
∠A=∠D,∠B=∠E,∠C=∠F.
A
B
C
D
E
F
(全等三角形对应边相等)
(全等三角形对应角相等)
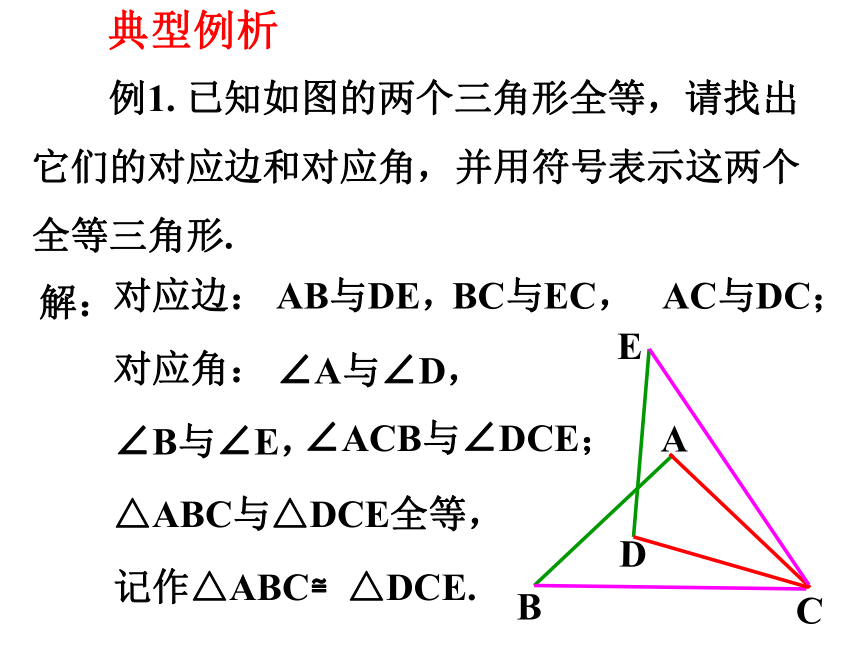
典型例析
例1. 已知如图的两个三角形全等,请找出它们的对应边和对应角,并用符号表示这两个全等三角形.
对应边:
对应角:
A
B
C
E
D
解:
AB与DE,
BC与EC,
AC与DC;
∠A与∠D,
∠B与∠E,
∠ACB与∠DCE;
△ABC与△DCE全等,
记作△ABC≌△DCE.
在全等三角形中寻找对应边、对应角的规律一般是:
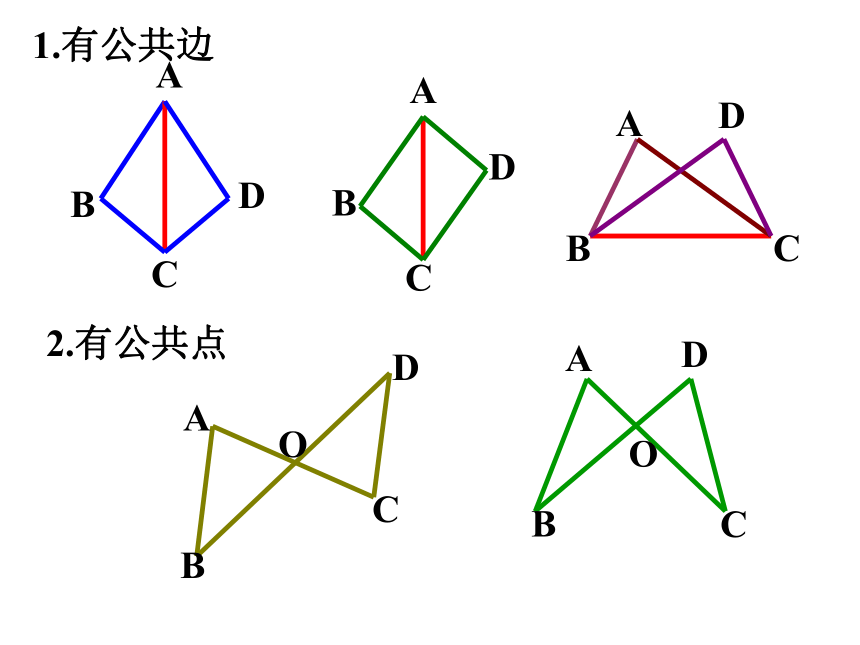
1.有公共边,则公共边为对应边.
2.有公共角,则公共角为对应角 (对顶角为对应角).
3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角.
4.对应角的对边为对应边.
5.对应边的对角为对应角.
6.根据书写规范,按照对应顶点找对应边或对应角.
1.有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2.有公共点
A
B
C
D
O
A
B
C
D
O
3.有公共角
A
B
C
D
E
A
B
D
C
E
例2.如图,已知E为线段AB上一点,AC⊥AB,DB⊥AB,△ACE≌△BED.试猜想CE与DE的位置关系,并证明你的结论.
解:
CE⊥DE.
∵AC⊥AB,
DB⊥AB,
∴∠A=∠B=90°,
∴∠C+∠CEA=90°.
A
B
D
E
C
∵△ACE≌△BED,
∴∠C=∠DEB.
∴∠DEB+∠CEA=90°.
∴∠CED=180°-(∠DEB+∠CEA)=90°.
∴CE⊥DE.
理由如下:
例3.如图,△ABE≌△ACD,点B、D、E、C在同一直线上.
(2)∠BAD与∠CAE有何关系?请说明理由.
(1)BD与CE相等吗?为什么?
解:(1)
理由如下:
BD=CE.
∵△ABE≌△ACD,
∴BE=CD.
∴BE-DE=CD-DE.
∴BD=CE.
A
B
E
D
C
例3.如图,△ABE≌△ACD,点B、D、E、C在同一直线上.
(2)∠BAD与∠CAE有何关系?
解:(2)
理由如下:
∠BAD=∠CAE.
∵△ABE≌△ACD,
∴ ∠BAE= ∠CAD.
∴∠BAE- ∠DAE= ∠CAD-DAE.
∴∠BAD= ∠CAE.
A
B
E
D
C
巩固新知
1.下列说法正确的是( ).
A.面积相等的两个图形全等
B.周长相等的两个图形全等
C.形状相同的两个图形全等
D.全等图形的形状和大小都相同
D
2.△ABC≌ △BAD,点A和点B、点C和点D是对应点,如果AB=6cm,BD=5cm,AD=7cm,那么BC 的长是( ).
A.7cm B.6cm C.5cm D.无法确定
A
A
C
D
B
3.△ABC≌ △BAD,点A和点B、点C和点D是对应点,则∠CAB的对应角是( ).
A.∠DAB B. ∠ DBA C. ∠ DBC D. ∠ CAD
C
A
C
D
B
4.如图,已知△ABC≌ △DEF,下列结论中,
不正确的是( ).
A.AB=DE B. BC=EF
C. BE=CF D. AC=DE
D
A
B
C
D
E
F
5.如图,已知△ABC≌ △CDB,AB ∥ CD,
则AB的对应边是( ).
A.BD B. BC C. CD D. AD
C
A
B
C
D
6.如图,已知△ABC≌ △BAD,若AB=5,
BD=6,AD=4,则BC等于( ).
A.6 B. 5 C. 4 D. 无法确定
C
A
B
C
D
7.如图,已知两个三角形全等,则α的度数是( ).
A.50° B. 72° C. 58° D. 无法确定
B
b
a
c
50°
58°
72°
α
a
c
8.若△AOC≌△BOD,AC= ,∠A= .
A
B
O
C
D
请填空
BD
∠B
公共点
9.若△ABD≌△ACE,BD= ,∠BDA= .
CE
∠CEA
A
B
C
D
E
公共角
A
B
C
D
E
F
10.已知△ABC≌△DEF,则AB边的对应边
为 ,∠C的对应角为 .
DE
∠F
11.如图,已知△ABD≌△ACE,且∠C=45°,
AC = 8,AE = 5,则∠B= , DC = .
A
E
B
C
D
45°
3
8
5
5
12.如图,已知E在线段AC上,点D在AB上,△ADC≌△EDB,且∠A=∠DEA. 若∠A:∠C
=5:3,求∠EDC的度数.
A
B
D
E
C
解:
∵∠A:∠C=5:3,
设∠A=5x,
∴∠C=3x.
∵∠A=∠DEA,
∴∠DEA=5x,
∵∠DEA=∠C+∠EDC,
∴∠EDC
∴∠ADE=180°- (∠A+∠DEA)
=180°-10x.
=∠DEA-∠C
=5x-3x
=2x
解:
∵∠A:∠C=5:3,
A
B
D
E
C
设∠A=5x,
∴∠C=3x.
∵∠A=∠DEA,
∴∠DEA=5x,
∵∠DEA=∠C+∠EDC,
∴∠EDC
∵△ADC≌△EDB,
∴∠ADE=180°- (∠A+∠DEA)
∴∠ADC=∠EDB.
∴∠BDC=∠ADE=180°-10x.
∵∠ADE+∠EDC+∠BDC=180°,
=180°-10x.
=∠DEA-∠C=5x-3x
=2x.
∴180°-10x +2x+180°-10x =180°.
∴x=10°,
∴∠EDC=20°.
今天作业
课本P33页第2、4、5、6 题
谢谢
人教版 八年级上册
12.1 全等三角形
学习目标
1.理解并掌握全等三角形的概念及其基本性质.(重点)
2.能找准全等三角形的对应边,理解全等三角形的对应角相等.(难点)
3.能进行简单的推理和计算,并解决一些实际问题.(难点)
看一看,下列同类的图形有什么特点.
形状和大小完全相同.
能够完全重合的两个图形称为全等形.
1.全等形的定义.
能够完全重合的两个三角形称为全等三角形.
2.全等三角形的定义.
A
B
C
D
E
F
学习新知
3.把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
你能指出上面两个全等三角形的对应顶点、
对应边、对应角吗?
A
B
C
D
E
F
N
M
S
O
T
D
C
O
A
B
A
B
C
D
E
F
平移、旋转、翻折前后的两个三角形的位置改变,但形状、大小不变.
“全等”用符号“≌ ”,
4.全等三角形的表示法
记作△ABC≌ △DEF,
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
A
B
C
D
E
F
读作△ABC全等于△DEF.
表示图中的△ABC和△DEF全等,
N
M
S
O
T
D
C
O
A
B
全等三角形的对应边相等;
5.全等三角形的性质
全等三角形的对应角相等.
6.全等三角形的几何语言
∵△ABC≌△DEF(已知),
∴AB=DE,AC=DF,BC=EF.
∠A=∠D,∠B=∠E,∠C=∠F.
A
B
C
D
E
F
(全等三角形对应边相等)
(全等三角形对应角相等)
典型例析
例1. 已知如图的两个三角形全等,请找出它们的对应边和对应角,并用符号表示这两个全等三角形.
对应边:
对应角:
A
B
C
E
D
解:
AB与DE,
BC与EC,
AC与DC;
∠A与∠D,
∠B与∠E,
∠ACB与∠DCE;
△ABC与△DCE全等,
记作△ABC≌△DCE.
在全等三角形中寻找对应边、对应角的规律一般是:
1.有公共边,则公共边为对应边.
2.有公共角,则公共角为对应角 (对顶角为对应角).
3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角.
4.对应角的对边为对应边.
5.对应边的对角为对应角.
6.根据书写规范,按照对应顶点找对应边或对应角.
1.有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2.有公共点
A
B
C
D
O
A
B
C
D
O
3.有公共角
A
B
C
D
E
A
B
D
C
E
例2.如图,已知E为线段AB上一点,AC⊥AB,DB⊥AB,△ACE≌△BED.试猜想CE与DE的位置关系,并证明你的结论.
解:
CE⊥DE.
∵AC⊥AB,
DB⊥AB,
∴∠A=∠B=90°,
∴∠C+∠CEA=90°.
A
B
D
E
C
∵△ACE≌△BED,
∴∠C=∠DEB.
∴∠DEB+∠CEA=90°.
∴∠CED=180°-(∠DEB+∠CEA)=90°.
∴CE⊥DE.
理由如下:
例3.如图,△ABE≌△ACD,点B、D、E、C在同一直线上.
(2)∠BAD与∠CAE有何关系?请说明理由.
(1)BD与CE相等吗?为什么?
解:(1)
理由如下:
BD=CE.
∵△ABE≌△ACD,
∴BE=CD.
∴BE-DE=CD-DE.
∴BD=CE.
A
B
E
D
C
例3.如图,△ABE≌△ACD,点B、D、E、C在同一直线上.
(2)∠BAD与∠CAE有何关系?
解:(2)
理由如下:
∠BAD=∠CAE.
∵△ABE≌△ACD,
∴ ∠BAE= ∠CAD.
∴∠BAE- ∠DAE= ∠CAD-DAE.
∴∠BAD= ∠CAE.
A
B
E
D
C
巩固新知
1.下列说法正确的是( ).
A.面积相等的两个图形全等
B.周长相等的两个图形全等
C.形状相同的两个图形全等
D.全等图形的形状和大小都相同
D
2.△ABC≌ △BAD,点A和点B、点C和点D是对应点,如果AB=6cm,BD=5cm,AD=7cm,那么BC 的长是( ).
A.7cm B.6cm C.5cm D.无法确定
A
A
C
D
B
3.△ABC≌ △BAD,点A和点B、点C和点D是对应点,则∠CAB的对应角是( ).
A.∠DAB B. ∠ DBA C. ∠ DBC D. ∠ CAD
C
A
C
D
B
4.如图,已知△ABC≌ △DEF,下列结论中,
不正确的是( ).
A.AB=DE B. BC=EF
C. BE=CF D. AC=DE
D
A
B
C
D
E
F
5.如图,已知△ABC≌ △CDB,AB ∥ CD,
则AB的对应边是( ).
A.BD B. BC C. CD D. AD
C
A
B
C
D
6.如图,已知△ABC≌ △BAD,若AB=5,
BD=6,AD=4,则BC等于( ).
A.6 B. 5 C. 4 D. 无法确定
C
A
B
C
D
7.如图,已知两个三角形全等,则α的度数是( ).
A.50° B. 72° C. 58° D. 无法确定
B
b
a
c
50°
58°
72°
α
a
c
8.若△AOC≌△BOD,AC= ,∠A= .
A
B
O
C
D
请填空
BD
∠B
公共点
9.若△ABD≌△ACE,BD= ,∠BDA= .
CE
∠CEA
A
B
C
D
E
公共角
A
B
C
D
E
F
10.已知△ABC≌△DEF,则AB边的对应边
为 ,∠C的对应角为 .
DE
∠F
11.如图,已知△ABD≌△ACE,且∠C=45°,
AC = 8,AE = 5,则∠B= , DC = .
A
E
B
C
D
45°
3
8
5
5
12.如图,已知E在线段AC上,点D在AB上,△ADC≌△EDB,且∠A=∠DEA. 若∠A:∠C
=5:3,求∠EDC的度数.
A
B
D
E
C
解:
∵∠A:∠C=5:3,
设∠A=5x,
∴∠C=3x.
∵∠A=∠DEA,
∴∠DEA=5x,
∵∠DEA=∠C+∠EDC,
∴∠EDC
∴∠ADE=180°- (∠A+∠DEA)
=180°-10x.
=∠DEA-∠C
=5x-3x
=2x
解:
∵∠A:∠C=5:3,
A
B
D
E
C
设∠A=5x,
∴∠C=3x.
∵∠A=∠DEA,
∴∠DEA=5x,
∵∠DEA=∠C+∠EDC,
∴∠EDC
∵△ADC≌△EDB,
∴∠ADE=180°- (∠A+∠DEA)
∴∠ADC=∠EDB.
∴∠BDC=∠ADE=180°-10x.
∵∠ADE+∠EDC+∠BDC=180°,
=180°-10x.
=∠DEA-∠C=5x-3x
=2x.
∴180°-10x +2x+180°-10x =180°.
∴x=10°,
∴∠EDC=20°.
今天作业
课本P33页第2、4、5、6 题
谢谢
