12.2 三角形全等的判定(1)课件(共24张PPT)
文档属性
| 名称 | 12.2 三角形全等的判定(1)课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 06:20:54 | ||
图片预览





文档简介
(共24张PPT)
12.2三角形全等的判定 (1)
人教版 八年级上册
A
B
C
D
E
F
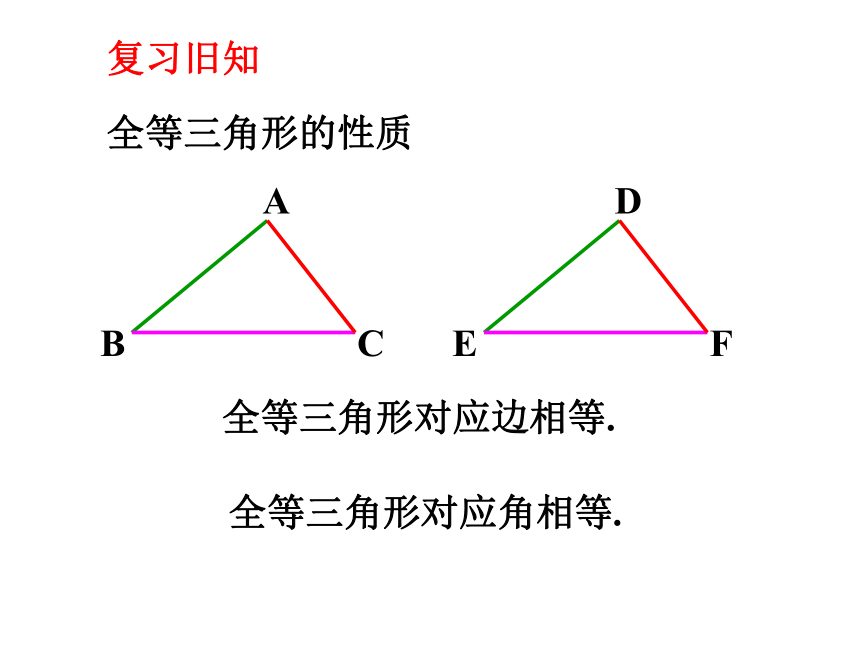
全等三角形的性质
全等三角形对应边相等.
全等三角形对应角相等.
复习旧知
1.已知三角形的一边长AB=5cm,画△ABC.
2.已知三角形的一边长AB=5cm,BC=4cm,
画△ABC.
画得的△ABC的形状和大小一样吗?
画得的△ABC的形状和大小一样吗?
学习新知
画法:
A
C
B
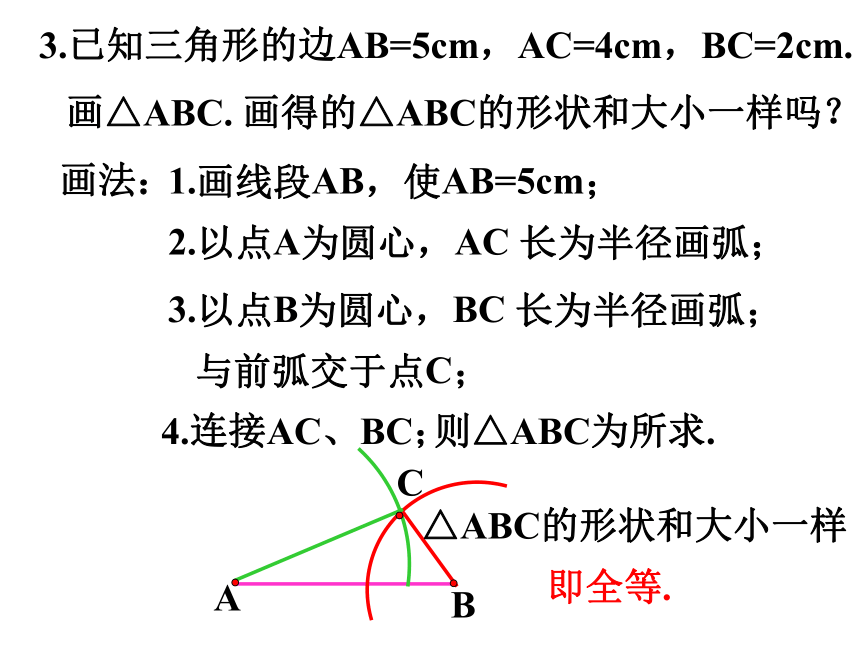
1.画线段AB,使AB=5cm;
2.以点A为圆心,AC 长为半径画弧;
3.以点B为圆心,BC 长为半径画弧;
与前弧交于点C;
4.连接AC、BC;
则△ABC为所求.
3.已知三角形的边AB=5cm,AC=4cm,BC=2cm.
画△ABC.
画得的△ABC的形状和大小一样吗?
△ABC的形状和大小一样
即全等.
判定两个三角形全等的方法一:
三边分别相等的两个三角形全等.
可以简写成“边边边”
或“SSS”.
∴ △ABC △ADC
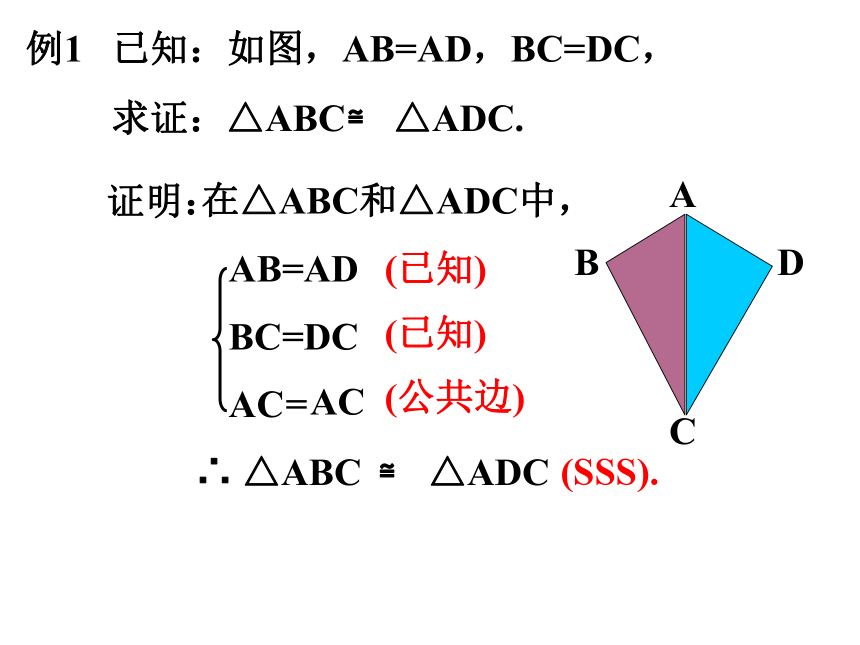
例1 已知:如图,AB=AD,BC=DC,
求证:△ABC≌ △ADC.
A
B
C
D
AC
AC
≌
证明:
=
(已知)
(已知)
(公共边)
(SSS).
在△ABC和△ADC中,
AB=AD
BC=DC
例2:如图所示,△ABC是一个钢架AB=AC,AD是连接点A与BC中点D的支架.
求证:△ABD≌△ACD.
A
B
C
D
证明:
∵D是BC的中点,
∴BD=CD.
在△ABD和△ACD中,
AB=AC
BD=CD
AD=AD
∴△ABD≌△ACD
(SSS).
(已知)
(已证)
(公共边)
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中;
摆出三个条件用大括号括起来;
写出全等结论.
证明全等的书写步骤:
∴ △ABD ≌△DCB
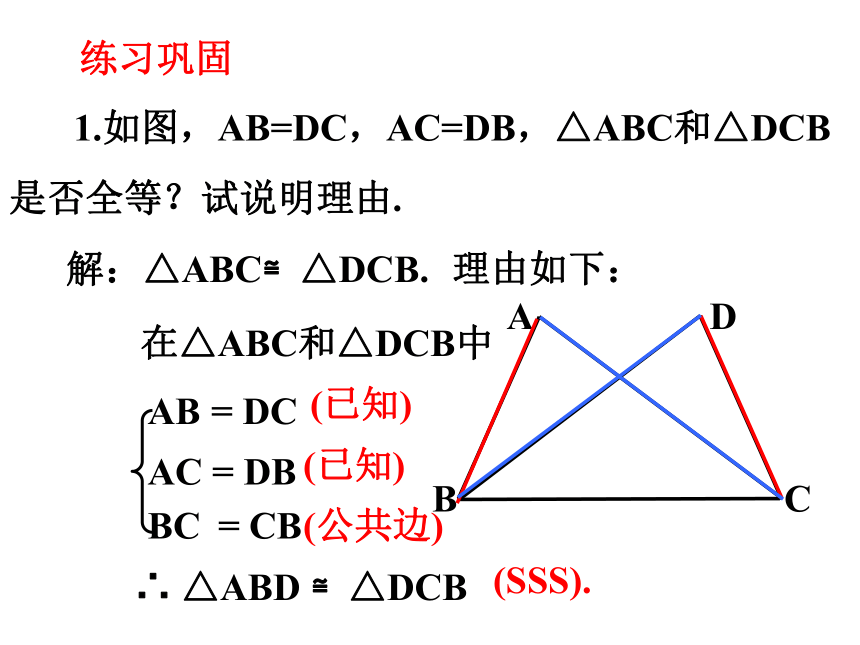
1.如图,AB=DC,AC=DB,△ABC和△DCB是否全等?试说明理由.
BC
CB
A
B
C
D
解:△ABC≌△DCB.
AB = DC
AC = DB
在△ABC和△DCB中
=
(SSS).
练习巩固
理由如下:
(已知)
(已知)
(公共边)
2.如图,在四边形ABCD中,AB=CD,AD=CB. 求证:∠ A= ∠ C.
D
A
B
C
证明:
AB=CD
AD=CB
BD=DB
∴△ABD≌△CDB
∴ ∠A= ∠C
你能说明AB∥CD吗?
(全等三角形的对应角相等)
(SSS).
在△ABD和△CDB中
∵ △ABD≌△CDB,
∴ ∠ABD= ∠CDB
∴AB∥CD.
(已知)
(已知)
(公共边)
3.如图,点B、E、C、F在一条直线上,AB=DC,
AE=DF,BF=CE.
证明:
AB=DC
AE=DF
BE=CF
∴△ABE≌△DCF
D
A
B
C
E
F
在△ABE和△DCF中
∵BF=CE,
∴BF-EF=CE-EF,
∴BE=CF.
(SSS).
求证:△ABE≌△DCF.
(已知)
(已知)
(已证)
小结
2. 三边对应相等的两个三角形全等
(边边边或SSS);
3.书写格式:①准备条件;
②三角形全等书写的三步骤.
1.知道三角形三条边的长度怎样画三角形.
1.根据下列条件,能够画出唯一△ABC的是( )
A. AB=5cm,AC=4cm
B. AC=4cm,BC=6cm.
C. AB=5cm,AC=2cm,BC=3cm.
D. AB=5cm,AC=4cm,BC=6cm.
D
巩固新知
2.如图,在△ABC中,AB=AC,BE=CE,
则由“SSS”可以判定( )
A.△ABD≌△ACD B.△BDE≌△CDE
C.△ABE≌△ACE D.以上都不对
C
D
A
B
C
E
3.如图,AB=DC,AC=DB,∠ABC= 80°,
∠CBD= 30°,则∠A= .
A
B
C
D
70°
4.如图,在△ABC中,AB=AC,点D,E在边BC上,且AD=AE,BE=CD.若∠BAC= 100°,
∠DAE= 60°,则∠BAD= .
20°
A
B
C
D
E
5.如图所示,C是AB的中点, AD=CE,CD=CE, 求证:△ABD≌△ACD.
A
B
C
D
证明:
∵C是AB的中点,
∴AC=BC.
在△ACD和△CBE中,
AC=CB
AD=CE
CD=BE
∴△ACD≌△CBE
(SSS).
E
6.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?
证明:在△CMO和△CNO中
OM=ON
CM=CN
CO=CO
∴△CMO≌△CNO
∴ ∠COM=∠CON
(全等三角形的对应角相等)
(SSS)
(已知)
(已知)
(公共边)
7.如图,点A,D,C,F在同一直线上,且AB=DE,AD=CF,BC=EF.若∠A= 55°,
∠B= 88°,求∠F的度数.
A
B
C
D
E
F
△ABC≌△DEF
AD=CF,
AC=DF.
∠F= ∠ACB.
∠F= ?.
要求
A
B
C
D
E
F
解:
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF
在△ABC和△DEF中
∵AD=CF,
∴AD+DC=CF+DC,
∴AC=DF.
(SSS).
∴ ∠F= ∠ACB.
在△ABC ∵ ∠A= 55°,∠B= 88°,
∴ ∠ACB=180°- ∠ A- ∠ B
= 37°.
∴ ∠F= 37°.
(已知)
(已证)
(已知)
今天作业
课本P43页第1题
课本P44页第9题
画法:
E
F
D
M
已知,△ABC,
画△DEF,
使△ABC≌△DEF.
A
B
C
1.画一条射线EM,在EM上截取EF,使EF=BC;
2.以点E为圆心,BA 长为半径画弧;
3.以点F为圆心,CA 长为半径画弧;
与前弧交于点D;
4.连接DE、DF;
则△DEF为所求.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.2三角形全等的判定 (1)
人教版 八年级上册
A
B
C
D
E
F
全等三角形的性质
全等三角形对应边相等.
全等三角形对应角相等.
复习旧知
1.已知三角形的一边长AB=5cm,画△ABC.
2.已知三角形的一边长AB=5cm,BC=4cm,
画△ABC.
画得的△ABC的形状和大小一样吗?
画得的△ABC的形状和大小一样吗?
学习新知
画法:
A
C
B
1.画线段AB,使AB=5cm;
2.以点A为圆心,AC 长为半径画弧;
3.以点B为圆心,BC 长为半径画弧;
与前弧交于点C;
4.连接AC、BC;
则△ABC为所求.
3.已知三角形的边AB=5cm,AC=4cm,BC=2cm.
画△ABC.
画得的△ABC的形状和大小一样吗?
△ABC的形状和大小一样
即全等.
判定两个三角形全等的方法一:
三边分别相等的两个三角形全等.
可以简写成“边边边”
或“SSS”.
∴ △ABC △ADC
例1 已知:如图,AB=AD,BC=DC,
求证:△ABC≌ △ADC.
A
B
C
D
AC
AC
≌
证明:
=
(已知)
(已知)
(公共边)
(SSS).
在△ABC和△ADC中,
AB=AD
BC=DC
例2:如图所示,△ABC是一个钢架AB=AC,AD是连接点A与BC中点D的支架.
求证:△ABD≌△ACD.
A
B
C
D
证明:
∵D是BC的中点,
∴BD=CD.
在△ABD和△ACD中,
AB=AC
BD=CD
AD=AD
∴△ABD≌△ACD
(SSS).
(已知)
(已证)
(公共边)
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中;
摆出三个条件用大括号括起来;
写出全等结论.
证明全等的书写步骤:
∴ △ABD ≌△DCB
1.如图,AB=DC,AC=DB,△ABC和△DCB是否全等?试说明理由.
BC
CB
A
B
C
D
解:△ABC≌△DCB.
AB = DC
AC = DB
在△ABC和△DCB中
=
(SSS).
练习巩固
理由如下:
(已知)
(已知)
(公共边)
2.如图,在四边形ABCD中,AB=CD,AD=CB. 求证:∠ A= ∠ C.
D
A
B
C
证明:
AB=CD
AD=CB
BD=DB
∴△ABD≌△CDB
∴ ∠A= ∠C
你能说明AB∥CD吗?
(全等三角形的对应角相等)
(SSS).
在△ABD和△CDB中
∵ △ABD≌△CDB,
∴ ∠ABD= ∠CDB
∴AB∥CD.
(已知)
(已知)
(公共边)
3.如图,点B、E、C、F在一条直线上,AB=DC,
AE=DF,BF=CE.
证明:
AB=DC
AE=DF
BE=CF
∴△ABE≌△DCF
D
A
B
C
E
F
在△ABE和△DCF中
∵BF=CE,
∴BF-EF=CE-EF,
∴BE=CF.
(SSS).
求证:△ABE≌△DCF.
(已知)
(已知)
(已证)
小结
2. 三边对应相等的两个三角形全等
(边边边或SSS);
3.书写格式:①准备条件;
②三角形全等书写的三步骤.
1.知道三角形三条边的长度怎样画三角形.
1.根据下列条件,能够画出唯一△ABC的是( )
A. AB=5cm,AC=4cm
B. AC=4cm,BC=6cm.
C. AB=5cm,AC=2cm,BC=3cm.
D. AB=5cm,AC=4cm,BC=6cm.
D
巩固新知
2.如图,在△ABC中,AB=AC,BE=CE,
则由“SSS”可以判定( )
A.△ABD≌△ACD B.△BDE≌△CDE
C.△ABE≌△ACE D.以上都不对
C
D
A
B
C
E
3.如图,AB=DC,AC=DB,∠ABC= 80°,
∠CBD= 30°,则∠A= .
A
B
C
D
70°
4.如图,在△ABC中,AB=AC,点D,E在边BC上,且AD=AE,BE=CD.若∠BAC= 100°,
∠DAE= 60°,则∠BAD= .
20°
A
B
C
D
E
5.如图所示,C是AB的中点, AD=CE,CD=CE, 求证:△ABD≌△ACD.
A
B
C
D
证明:
∵C是AB的中点,
∴AC=BC.
在△ACD和△CBE中,
AC=CB
AD=CE
CD=BE
∴△ACD≌△CBE
(SSS).
E
6.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?
证明:在△CMO和△CNO中
OM=ON
CM=CN
CO=CO
∴△CMO≌△CNO
∴ ∠COM=∠CON
(全等三角形的对应角相等)
(SSS)
(已知)
(已知)
(公共边)
7.如图,点A,D,C,F在同一直线上,且AB=DE,AD=CF,BC=EF.若∠A= 55°,
∠B= 88°,求∠F的度数.
A
B
C
D
E
F
△ABC≌△DEF
AD=CF,
AC=DF.
∠F= ∠ACB.
∠F= ?.
要求
A
B
C
D
E
F
解:
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF
在△ABC和△DEF中
∵AD=CF,
∴AD+DC=CF+DC,
∴AC=DF.
(SSS).
∴ ∠F= ∠ACB.
在△ABC ∵ ∠A= 55°,∠B= 88°,
∴ ∠ACB=180°- ∠ A- ∠ B
= 37°.
∴ ∠F= 37°.
(已知)
(已证)
(已知)
今天作业
课本P43页第1题
课本P44页第9题
画法:
E
F
D
M
已知,△ABC,
画△DEF,
使△ABC≌△DEF.
A
B
C
1.画一条射线EM,在EM上截取EF,使EF=BC;
2.以点E为圆心,BA 长为半径画弧;
3.以点F为圆心,CA 长为半径画弧;
与前弧交于点D;
4.连接DE、DF;
则△DEF为所求.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
