12.2三角形全等的判定(2)课件(共24张PPT)
文档属性
| 名称 | 12.2三角形全等的判定(2)课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 00:00:00 | ||
图片预览

文档简介
(共24张PPT)
12.2三角形全等的判定 (2)
人教版 八年级上册
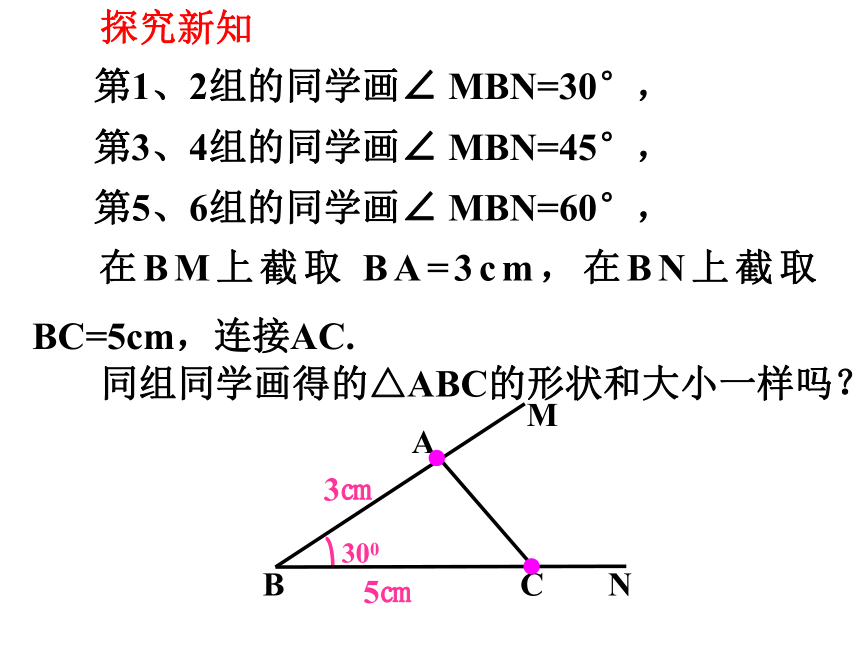
第1、2组的同学画∠ MBN=30°,
5㎝
3㎝
A
C
第3、4组的同学画∠ MBN=45°,
第5、6组的同学画∠ MBN=60°,
在BM上截取 BA=3cm,在BN上截取BC=5cm,连接AC.
同组同学画得的△ABC的形状和大小一样吗?
300
B
M
N
探究新知
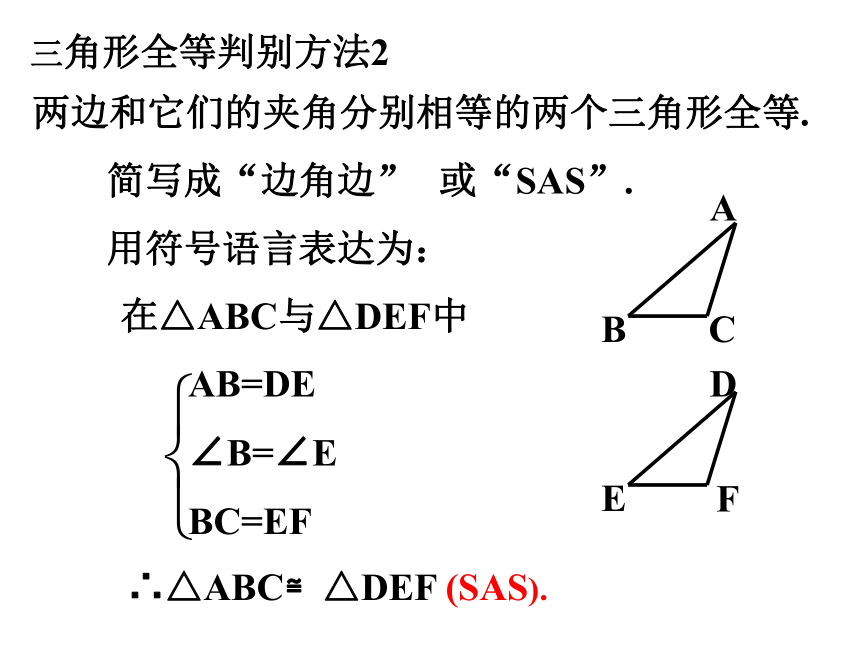
三角形全等判别方法2
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF
A
B
C
D
E
F
两边和它们的夹角分别相等的两个三角形全等.
简写成“边角边”
或“SAS”.
(SAS).
认识新知
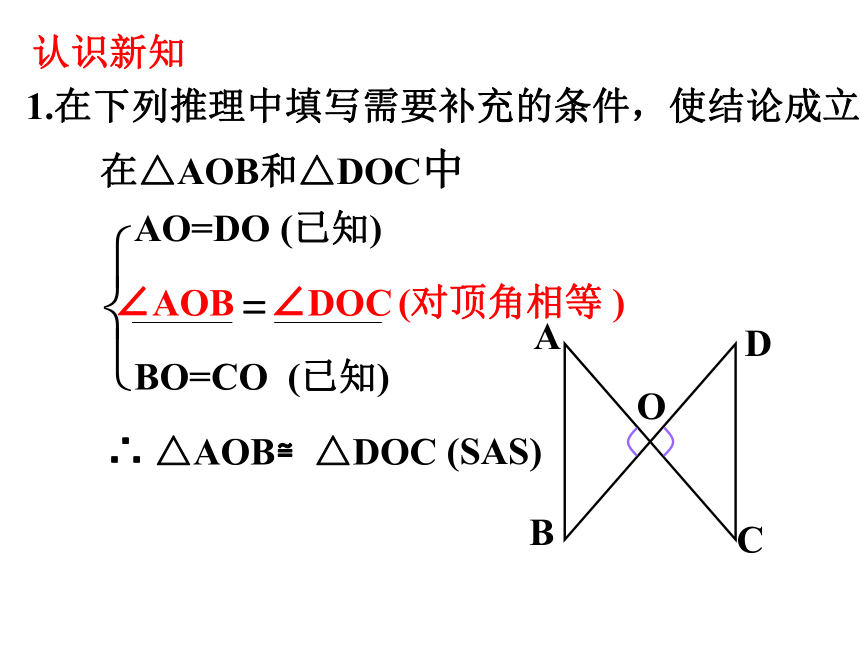
1.在下列推理中填写需要补充的条件,使结论成立
在△AOB和△DOC中
=
(对顶角相等 )
BO=CO (已知)
∴ △AOB≌△DOC
A
B
O
D
C
∠AOB
∠DOC
(SAS)
AO=DO (已知)
(已知)
(公共角)
A
D
C
B
E
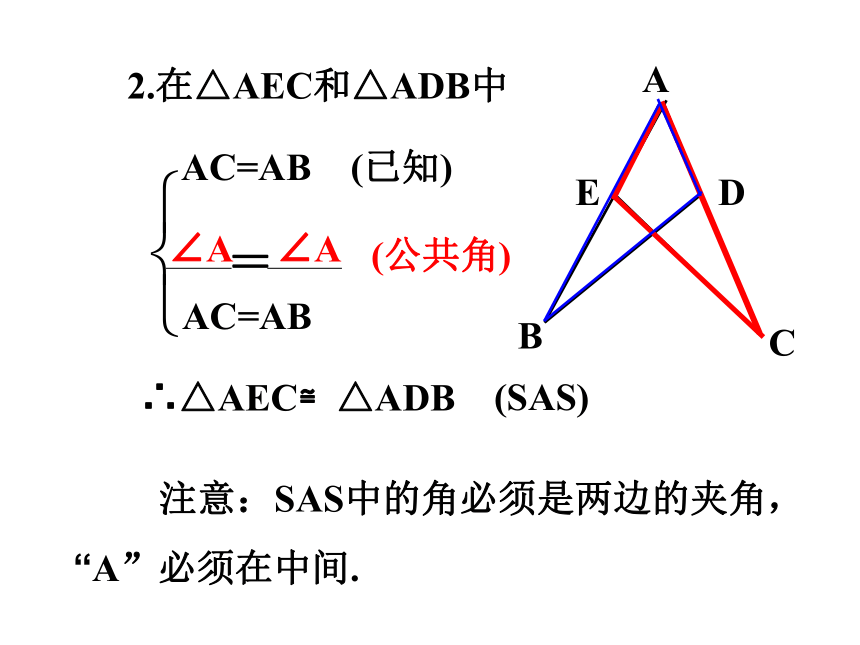
∴△AEC≌△ADB
2.在△AEC和△ADB中
AC=AB
注意:SAS中的角必须是两边的夹角,
“A”必须在中间.
=
(SAS)
∠A
∠A
AC=AB
B
A
C
D
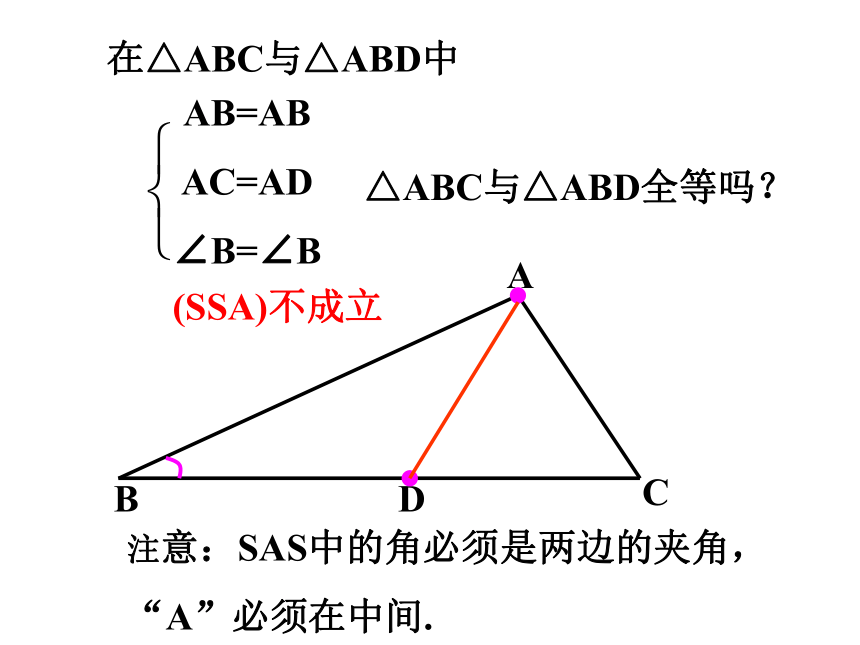
在△ABC与△ABD中
AB=AB
AC=AD
∠B=∠B
△ABC与△ABD全等吗?
注意:SAS中的角必须是两边的夹角,
“A”必须在中间.
(SSA)不成立
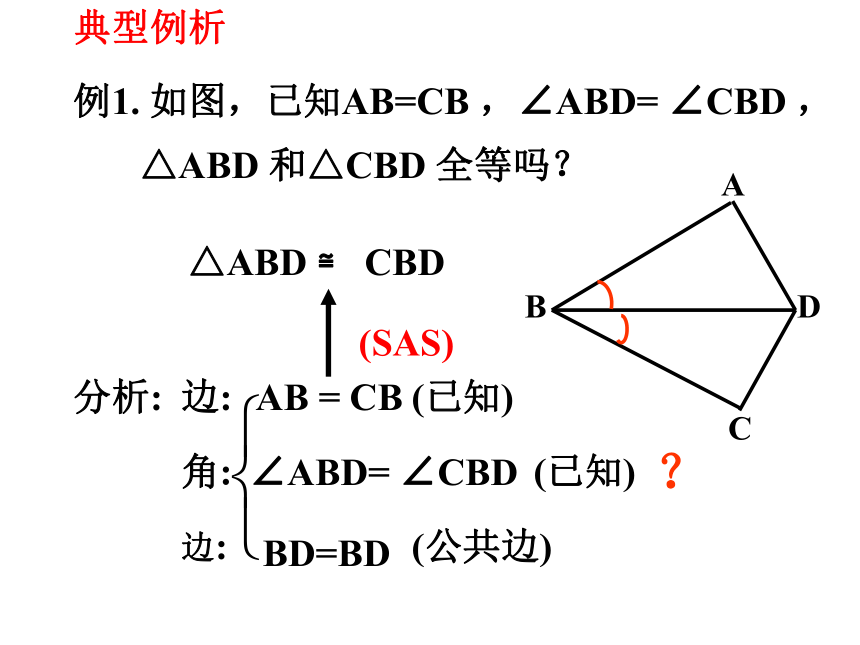
例1. 如图,已知AB=CB ,∠ABD= ∠CBD ,
△ABD 和△CBD 全等吗?
分析:
△ABD ≌ CBD
边:
AB = CB
∠ABD= ∠CBD
?
A
B
C
D
(SAS)
BD=BD
(已知)
边:
(公共边)
角:
(已知)
典型例析
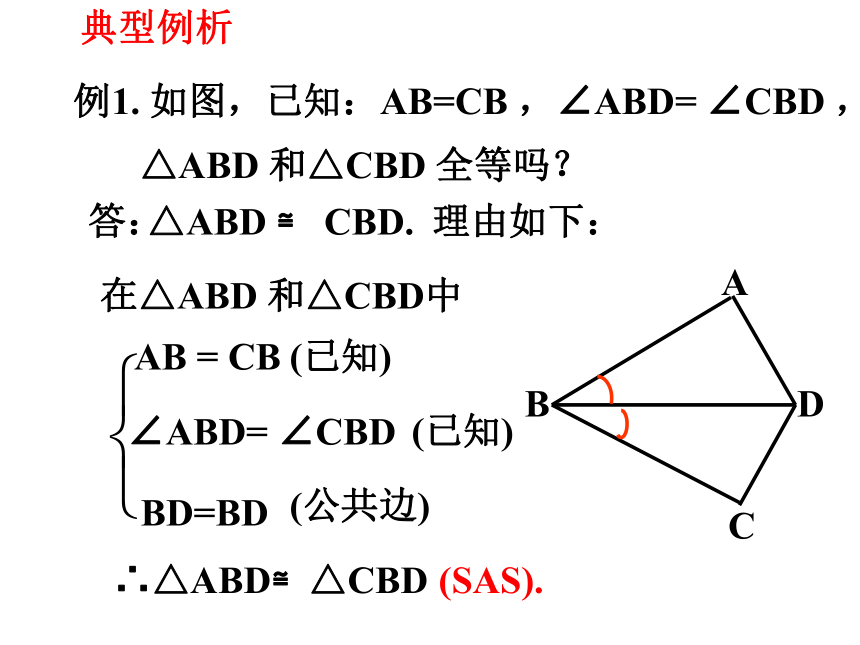
例1. 如图,已知:AB=CB ,∠ABD= ∠CBD ,
△ABD 和△CBD 全等吗?
△ABD ≌ CBD.
AB = CB
∠ABD= ∠CBD
A
B
C
D
BD=BD
(已知)
(公共边)
(已知)
典型例析
答:
理由如下:
在△ABD 和△CBD中
∴△ABD≌△CBD
(SAS).
F
A
B
D
C
E
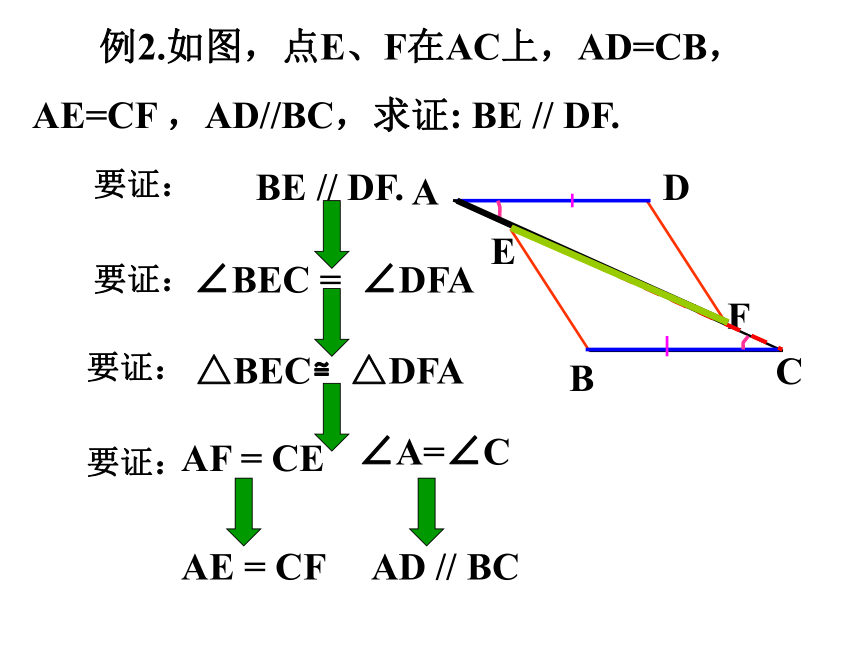
例2.如图,点E、F在AC上,AD=CB,AE=CF ,AD//BC,求证: BE // DF.
∠A=∠C
AD // BC
AE = CF
AF = CE
BE // DF.
∠BEC = ∠DFA
△BEC≌△DFA
要证:
要证:
要证:
要证:
F
A
B
D
C
E
∵AE=CF
∴AE+EF=CF+EF
∴AF=CE
∵AD//BC
∴∠A=∠C
证明:
(已知)
在△BEC和△DFA中
AD=CB
∠A=∠C
(已证)
AF=CE
∴ ∠BEC = ∠DFA,
(已证)
∴△BEC≌△DFA
(SAS)
∴ BE // DF.
例2.如图,点E、F在AC上,AD=CB,AE=CF ,AD//BC.求证: BE // DF.
1.根据下列条件,能够画出唯一△ABC的是( )
A. AB=6cm,BC=5cm, ∠A=50°
B. AC=5cm,BC=13cm, ∠A=50°
C. AB=6cm,BC=5cm, ∠B=50°.
D. AB=6cm,AC=5cm, ∠C=60°.
C
巩固新知
2.如图,已知BD=CD. 若要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是( ).
A.∠B=∠C
B.∠DAB=∠DAC
C.∠BDA=∠CDA
D.AD=AD
A
B
C
D
C
3. 如图,在△ABD中,已知∠A=∠B=50°,
AD=BF,AE=BD,则∠ EDF的度数是( ).
A
B
C
D
E
F
A.50° B. 60° C. 70° D. 无法确定
A
△ADE≌△BFD
∠ ADE= ∠BFD
∠ ADE +∠EDF
=∠B+∠BFD
提示
4. 如图,已知线段AC与BD相交于点E,AE=DE,
BE=CE,若AB=5,则CD的长为 .
A
B
C
D
5
5. 如图,在△ABC中,AD是BC边上的中线,
AB=9,AC=7,则AD的取值范围是 .
A
B
C
D
1<AD<8
E
DE=AD
∴△ADC≌△EDB
A
B
C
D
?
6.已知:AD=CD, BD 平分∠ADC .求证:∠A=∠C .
∵BD平分∠ADC,
∴ ∠ADB = ∠CDB.
证明:
(已知)
在△ADB和△CDB中
AB=AD
BD=BD
(公共边)
∠ADB = ∠CDB
∴△ADB≌△CDB
∴ ∠A= ∠C
(全等三角形的对应角相等).
(SAS).
(已证)
7.如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由.
A
B
C
D
答:能判断BC=AD.
理由如下:
(已知)
在△ABC和△BAD中
AC=BD
∠CAB=∠DBA
AB=BA
∴ BC = AD.
∴△ABC≌△BAD
(SAS).
(公共边)
(已知)
8.如图,点E、F在BC上,BE=CF, AB=DC, ∠B= ∠C.
求证:∠A=∠ D.
A
B
C
D
E
F
BF=CE
∠A = ∠D
△ABF≌△DCE
要证:
要证:
AE = CF
要证:
8.如图,点E、F在BC上,BE=CF, AB=DC, ∠B= ∠C.
求证:∠A=∠ D.
A
B
C
D
E
F
∵BE=CF,
∴BE+EF=CF+EF.
∴BF=CE.
证明:
在△ABF和△DCE中
AB=DC
∠B=∠C
BF=CE
∴ ∠A = ∠D.
∴△ABF≌△DCE
(SAS).
(全等三角形的对应角相等).
(已知)
(已知)
(已证)
课堂小结:
2. 求证两个三角形中的边或角相等时,一般
要先证明这两个三角形全等。
1.三角形全等的判定2:
两边和它们的夹角对应相等的两个三角形全等.
证明三角形全等的过程
1.准备条件
2.指明范围
3.摆齐根据
4.写出结论
今天作业
课本P43页第2题
课本P44页第10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.2三角形全等的判定 (2)
人教版 八年级上册
第1、2组的同学画∠ MBN=30°,
5㎝
3㎝
A
C
第3、4组的同学画∠ MBN=45°,
第5、6组的同学画∠ MBN=60°,
在BM上截取 BA=3cm,在BN上截取BC=5cm,连接AC.
同组同学画得的△ABC的形状和大小一样吗?
300
B
M
N
探究新知
三角形全等判别方法2
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF
A
B
C
D
E
F
两边和它们的夹角分别相等的两个三角形全等.
简写成“边角边”
或“SAS”.
(SAS).
认识新知
1.在下列推理中填写需要补充的条件,使结论成立
在△AOB和△DOC中
=
(对顶角相等 )
BO=CO (已知)
∴ △AOB≌△DOC
A
B
O
D
C
∠AOB
∠DOC
(SAS)
AO=DO (已知)
(已知)
(公共角)
A
D
C
B
E
∴△AEC≌△ADB
2.在△AEC和△ADB中
AC=AB
注意:SAS中的角必须是两边的夹角,
“A”必须在中间.
=
(SAS)
∠A
∠A
AC=AB
B
A
C
D
在△ABC与△ABD中
AB=AB
AC=AD
∠B=∠B
△ABC与△ABD全等吗?
注意:SAS中的角必须是两边的夹角,
“A”必须在中间.
(SSA)不成立
例1. 如图,已知AB=CB ,∠ABD= ∠CBD ,
△ABD 和△CBD 全等吗?
分析:
△ABD ≌ CBD
边:
AB = CB
∠ABD= ∠CBD
?
A
B
C
D
(SAS)
BD=BD
(已知)
边:
(公共边)
角:
(已知)
典型例析
例1. 如图,已知:AB=CB ,∠ABD= ∠CBD ,
△ABD 和△CBD 全等吗?
△ABD ≌ CBD.
AB = CB
∠ABD= ∠CBD
A
B
C
D
BD=BD
(已知)
(公共边)
(已知)
典型例析
答:
理由如下:
在△ABD 和△CBD中
∴△ABD≌△CBD
(SAS).
F
A
B
D
C
E
例2.如图,点E、F在AC上,AD=CB,AE=CF ,AD//BC,求证: BE // DF.
∠A=∠C
AD // BC
AE = CF
AF = CE
BE // DF.
∠BEC = ∠DFA
△BEC≌△DFA
要证:
要证:
要证:
要证:
F
A
B
D
C
E
∵AE=CF
∴AE+EF=CF+EF
∴AF=CE
∵AD//BC
∴∠A=∠C
证明:
(已知)
在△BEC和△DFA中
AD=CB
∠A=∠C
(已证)
AF=CE
∴ ∠BEC = ∠DFA,
(已证)
∴△BEC≌△DFA
(SAS)
∴ BE // DF.
例2.如图,点E、F在AC上,AD=CB,AE=CF ,AD//BC.求证: BE // DF.
1.根据下列条件,能够画出唯一△ABC的是( )
A. AB=6cm,BC=5cm, ∠A=50°
B. AC=5cm,BC=13cm, ∠A=50°
C. AB=6cm,BC=5cm, ∠B=50°.
D. AB=6cm,AC=5cm, ∠C=60°.
C
巩固新知
2.如图,已知BD=CD. 若要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是( ).
A.∠B=∠C
B.∠DAB=∠DAC
C.∠BDA=∠CDA
D.AD=AD
A
B
C
D
C
3. 如图,在△ABD中,已知∠A=∠B=50°,
AD=BF,AE=BD,则∠ EDF的度数是( ).
A
B
C
D
E
F
A.50° B. 60° C. 70° D. 无法确定
A
△ADE≌△BFD
∠ ADE= ∠BFD
∠ ADE +∠EDF
=∠B+∠BFD
提示
4. 如图,已知线段AC与BD相交于点E,AE=DE,
BE=CE,若AB=5,则CD的长为 .
A
B
C
D
5
5. 如图,在△ABC中,AD是BC边上的中线,
AB=9,AC=7,则AD的取值范围是 .
A
B
C
D
1<AD<8
E
DE=AD
∴△ADC≌△EDB
A
B
C
D
?
6.已知:AD=CD, BD 平分∠ADC .求证:∠A=∠C .
∵BD平分∠ADC,
∴ ∠ADB = ∠CDB.
证明:
(已知)
在△ADB和△CDB中
AB=AD
BD=BD
(公共边)
∠ADB = ∠CDB
∴△ADB≌△CDB
∴ ∠A= ∠C
(全等三角形的对应角相等).
(SAS).
(已证)
7.如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由.
A
B
C
D
答:能判断BC=AD.
理由如下:
(已知)
在△ABC和△BAD中
AC=BD
∠CAB=∠DBA
AB=BA
∴ BC = AD.
∴△ABC≌△BAD
(SAS).
(公共边)
(已知)
8.如图,点E、F在BC上,BE=CF, AB=DC, ∠B= ∠C.
求证:∠A=∠ D.
A
B
C
D
E
F
BF=CE
∠A = ∠D
△ABF≌△DCE
要证:
要证:
AE = CF
要证:
8.如图,点E、F在BC上,BE=CF, AB=DC, ∠B= ∠C.
求证:∠A=∠ D.
A
B
C
D
E
F
∵BE=CF,
∴BE+EF=CF+EF.
∴BF=CE.
证明:
在△ABF和△DCE中
AB=DC
∠B=∠C
BF=CE
∴ ∠A = ∠D.
∴△ABF≌△DCE
(SAS).
(全等三角形的对应角相等).
(已知)
(已知)
(已证)
课堂小结:
2. 求证两个三角形中的边或角相等时,一般
要先证明这两个三角形全等。
1.三角形全等的判定2:
两边和它们的夹角对应相等的两个三角形全等.
证明三角形全等的过程
1.准备条件
2.指明范围
3.摆齐根据
4.写出结论
今天作业
课本P43页第2题
课本P44页第10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
