12.2 三角形全等的判定(5)课件(共24张PPT)
文档属性
| 名称 | 12.2 三角形全等的判定(5)课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 06:24:56 | ||
图片预览


文档简介
(共24张PPT)
12.2三角形全等的判定 (5)
人教版 八年级上册
判断两个三角形全等的方法有:
(1): ;
(2): ;
(3): ;
(4): ;
SSS
SAS
ASA
AAS
AAA
?
SSA
?
复习旧知
B
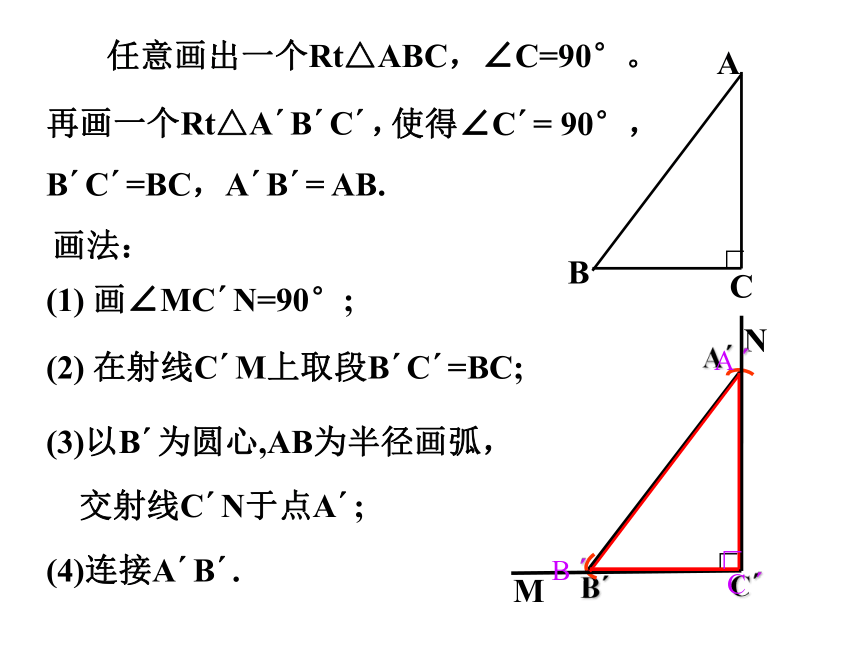
任意画出一个Rt△ABC,∠C=90°。
A
画法:
(1) 画∠MC N=90°;
(2) 在射线C M上取段B C =BC;
(3)以B 为圆心,AB为半径画弧,
交射线C N于点A ;
(4)连接A B .
∟
C
M
N
∟
B
C
A
∟
B
C
A
再画一个Rt△A B C ,
B C =BC,A B = AB.
使得∠C = 90°,
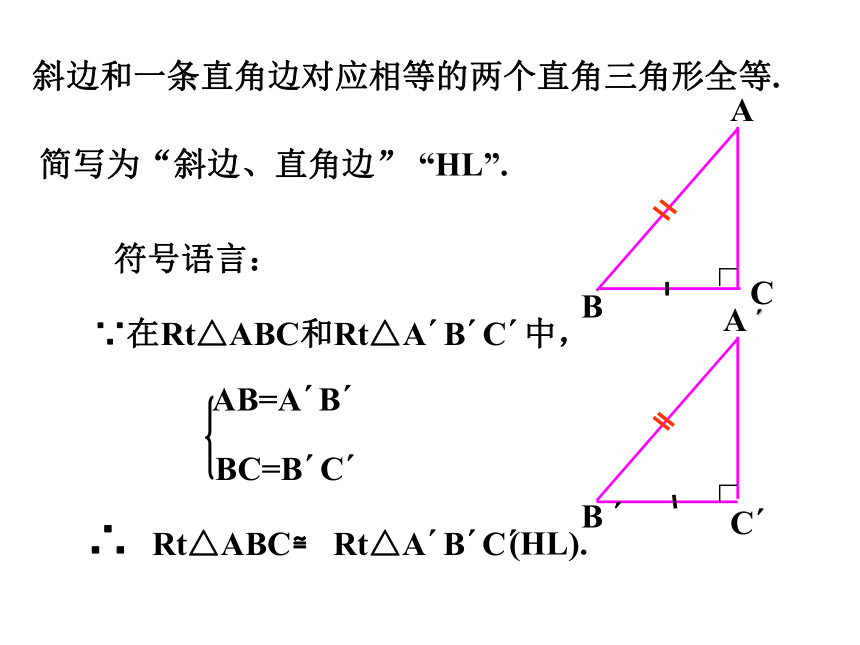
斜边和一条直角边对应相等的两个直角三角形全等.
符号语言:
AB=A B
∵在Rt△ABC和Rt△A B C 中,
Rt△ABC≌ Rt△A B C
∴
∟
B
C
A
∟
B
C
A
(HL).
BC=B C
简写为“斜边、直角边”
“HL”.
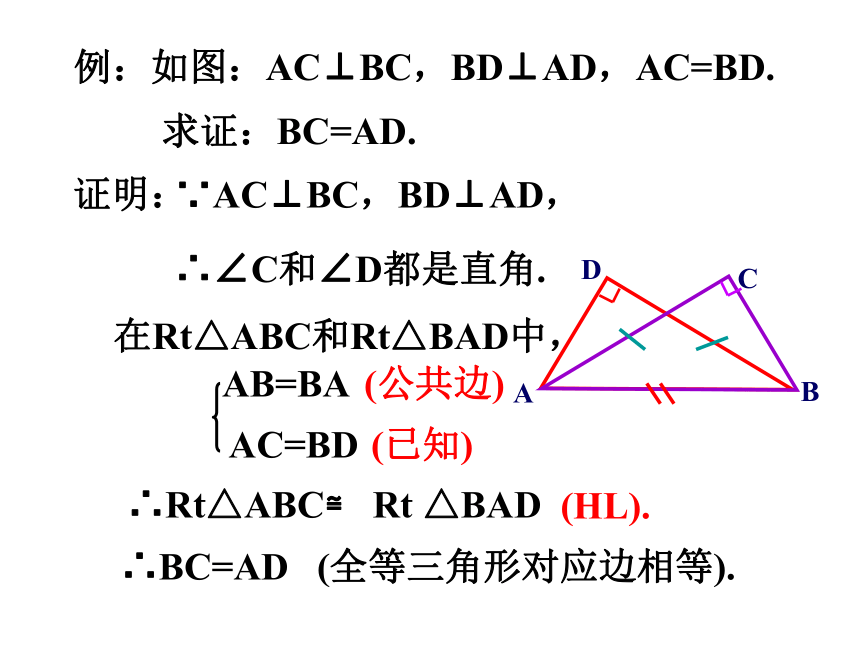
例:如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.
A
B
C
D
证明:
在Rt△ABC和Rt△BAD中,
AB=BA
∴Rt△ABC≌ Rt △BAD
∴BC=AD
(HL).
(全等三角形对应边相等).
∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角.
AC=BD
(公共边)
(已知)
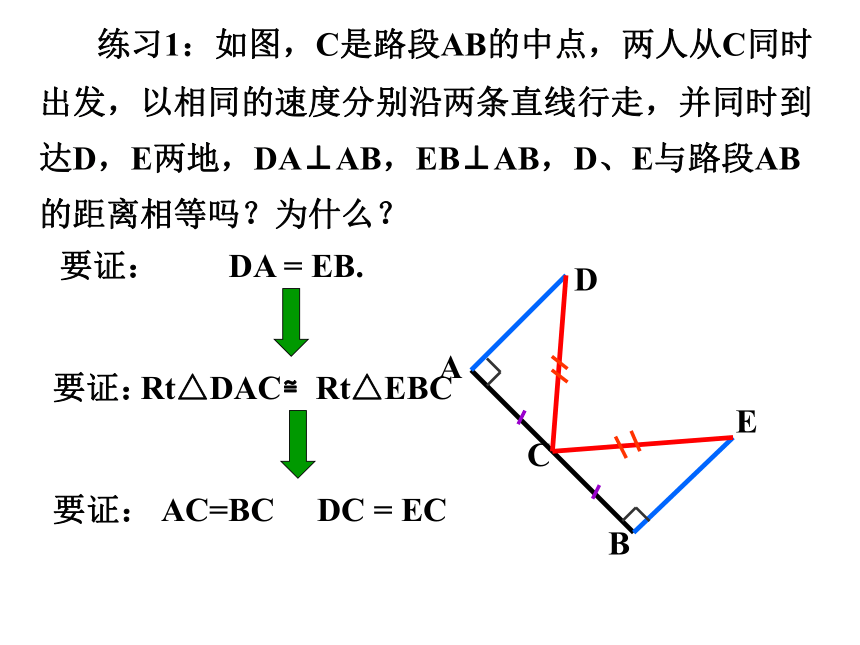
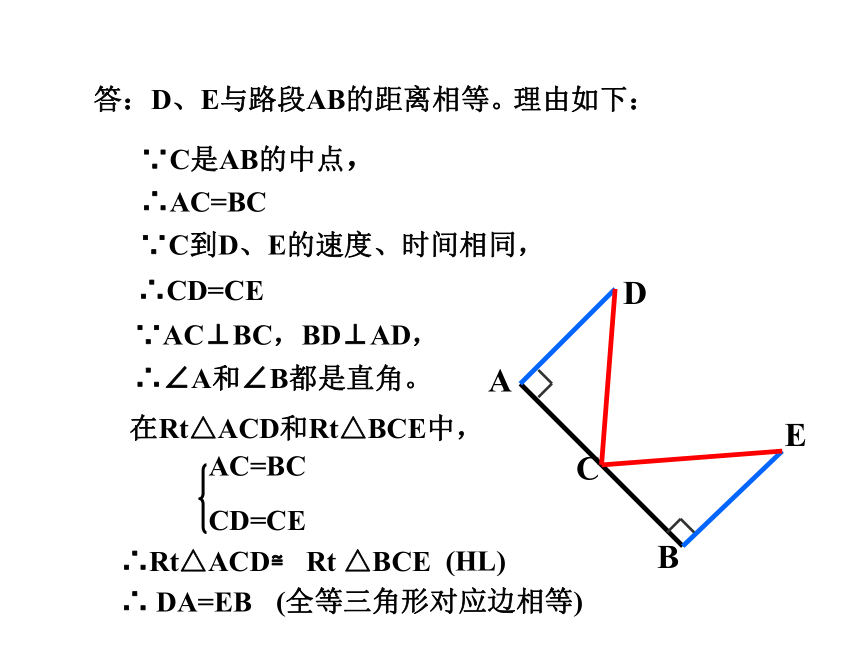
练习1:如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?
B
D
A
C
E
AC=BC
DA = EB.
Rt△DAC≌Rt△EBC
要证:
DC = EC
要证:
要证:
AC=BC
∴Rt△ACD≌ Rt △BCE
∴ DA=EB
在Rt△ACD和Rt△BCE中,
∵C是AB的中点,
∵C到D、E的速度、时间相同,
B
D
A
C
E
CD=CE
∴AC=BC
∴CD=CE
∵AC⊥BC,BD⊥AD,
∴∠A和∠B都是直角。
答:D、E与路段AB的距离相等。
(HL)
(全等三角形对应边相等)
理由如下:
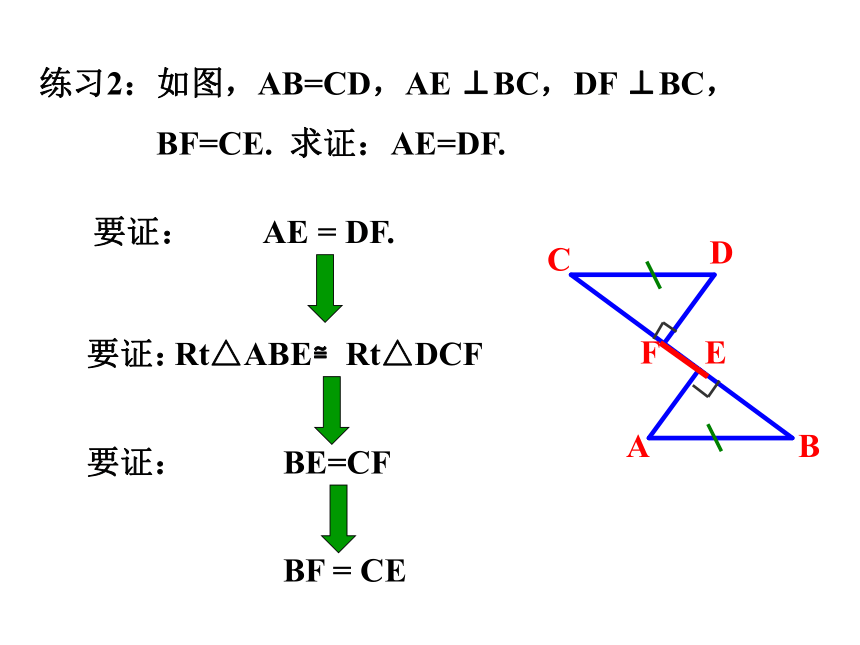
练习2:如图,AB=CD,AE ⊥BC,DF ⊥BC,
BF=CE. 求证:AE=DF.
A
B
C
D
E
F
BE=CF
AE = DF.
Rt△ABE≌Rt△DCF
要证:
要证:
BF = CE
要证:
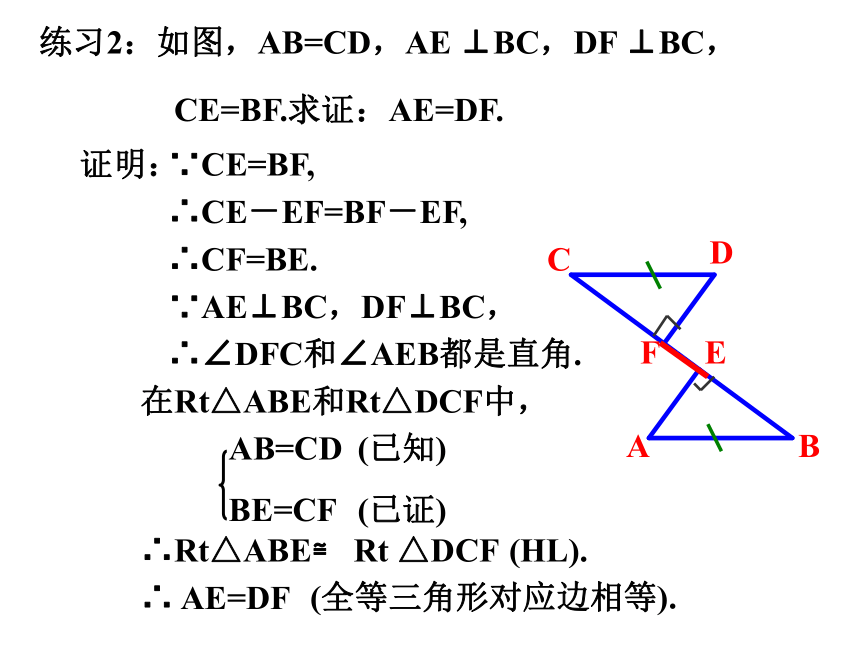
练习2:如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF.求证:AE=DF.
A
B
C
D
E
F
证明:
∵CE=BF,
∴CE-EF=BF-EF,
∴CF=BE.
∵AE⊥BC,DF⊥BC,
∴∠DFC和∠AEB都是直角.
AB=CD
∴Rt△ABE≌ Rt △DCF
∴ AE=DF
在Rt△ABE和Rt△DCF中,
BE=CF
(HL).
(全等三角形对应边相等).
(已证)
(已知)
1 . 如图,DE⊥AB,DF⊥BC,垂足分别是E,F,
DE =DF, ∠EDB= 60°,则 ∠EBF= 度,
BE= .
60
BF
E
B
D
F
A
C
练习3:
(4) ( )
(3) ( )
(2) ( )
(1) ( )
A
B
D
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
2.已知∠ACB =∠ADB=90°,要证明 △ABC≌ △BAD,还需一个什么条件? 写出这些条件,并写出判定全等的理由。
A
F
C
E
D
B
3.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF。
求证:BF=DE
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE.
证明:
AB=CD
∴Rt△ABF≌ Rt △CDE
∴ BF=DE
AF=CE
(HL).
(全等三角形对应边相等).
(已证)
(已知)
在Rt△ABF和Rt△CDE中,
∵BF⊥AC,DE⊥AC,
∴∠BFA和∠DEC都是直角.
1.如图,已知∠B=∠E =90°,AB=DE,AC=DF,则判定△ABC≌△DEF的依据是( ).
A.SAS B.ASA C.AAS D.HL
D
A
B
C
D
E
F
巩固新知
2.如图,已知∠C=∠D =90°. 若要根据“HL”判定△ABC≌△ABD,则还需添加的条件是( ).
A.∠BAC=∠BAD
B.∠ABC=∠ABD
C.AC=AD
D.AB=AB
C
A
B
C
D
3.下列条件中,不能判定两个直角三角形全等的是( ).
A.一个锐角和斜边分别相等
B.两条直角边分别相等
C.两个锐角分别相等
D.斜边和一条直角边分别相等
C
4.如图,BE ,CD是△ABC的高,则判定△BCD≌△CBE的依据是( ).
A.SAS B.ASA C. HL D. SSS
C
A
B
C
D
E
5.如图,在Rt△ABC中, ∠ BAC=90°,DE ⊥ BC于点E,AC=EC, ∠ ACB=60°,则∠ ACD度数是( ).
A.45° B.30° C. 20° D. 15°
B
A
B
C
D
E
6.如图,在△ABC中, AB=AC,AE是经过点A的一条直线,且B,C在AE的两侧,BD ⊥ AE于点D, CE ⊥ AE于点E,AD=CE,则∠ BAC度数是( ).
A.45° B.60° C. 90° D. 120°
C
C
A
B
D
E
7.如图,在Rt△ABC中,∠ACB=90°,
E是AB上一点,且BE=BC,DE⊥AB于E,
若AC=8,则AD + DE等于( ).
A.7 B.8 C.9 D.10
A
B
C
D
E
C
8. 如图,有一个直角△ABC,∠C=90°,AC=12,BC=5,一条线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AX上运动,
当AP= 时,才能使△ABC≌△PQA.
C
B
P
Q
A
x
X
5
9. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于 D,DE⊥AB于E,
且AB=6 cm,则△DEB的周长为_____cm.
A
B
C
D
E
6
今天作业
课本P44页第6、7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.2三角形全等的判定 (5)
人教版 八年级上册
判断两个三角形全等的方法有:
(1): ;
(2): ;
(3): ;
(4): ;
SSS
SAS
ASA
AAS
AAA
?
SSA
?
复习旧知
B
任意画出一个Rt△ABC,∠C=90°。
A
画法:
(1) 画∠MC N=90°;
(2) 在射线C M上取段B C =BC;
(3)以B 为圆心,AB为半径画弧,
交射线C N于点A ;
(4)连接A B .
∟
C
M
N
∟
B
C
A
∟
B
C
A
再画一个Rt△A B C ,
B C =BC,A B = AB.
使得∠C = 90°,
斜边和一条直角边对应相等的两个直角三角形全等.
符号语言:
AB=A B
∵在Rt△ABC和Rt△A B C 中,
Rt△ABC≌ Rt△A B C
∴
∟
B
C
A
∟
B
C
A
(HL).
BC=B C
简写为“斜边、直角边”
“HL”.
例:如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.
A
B
C
D
证明:
在Rt△ABC和Rt△BAD中,
AB=BA
∴Rt△ABC≌ Rt △BAD
∴BC=AD
(HL).
(全等三角形对应边相等).
∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角.
AC=BD
(公共边)
(已知)
练习1:如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?
B
D
A
C
E
AC=BC
DA = EB.
Rt△DAC≌Rt△EBC
要证:
DC = EC
要证:
要证:
AC=BC
∴Rt△ACD≌ Rt △BCE
∴ DA=EB
在Rt△ACD和Rt△BCE中,
∵C是AB的中点,
∵C到D、E的速度、时间相同,
B
D
A
C
E
CD=CE
∴AC=BC
∴CD=CE
∵AC⊥BC,BD⊥AD,
∴∠A和∠B都是直角。
答:D、E与路段AB的距离相等。
(HL)
(全等三角形对应边相等)
理由如下:
练习2:如图,AB=CD,AE ⊥BC,DF ⊥BC,
BF=CE. 求证:AE=DF.
A
B
C
D
E
F
BE=CF
AE = DF.
Rt△ABE≌Rt△DCF
要证:
要证:
BF = CE
要证:
练习2:如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF.求证:AE=DF.
A
B
C
D
E
F
证明:
∵CE=BF,
∴CE-EF=BF-EF,
∴CF=BE.
∵AE⊥BC,DF⊥BC,
∴∠DFC和∠AEB都是直角.
AB=CD
∴Rt△ABE≌ Rt △DCF
∴ AE=DF
在Rt△ABE和Rt△DCF中,
BE=CF
(HL).
(全等三角形对应边相等).
(已证)
(已知)
1 . 如图,DE⊥AB,DF⊥BC,垂足分别是E,F,
DE =DF, ∠EDB= 60°,则 ∠EBF= 度,
BE= .
60
BF
E
B
D
F
A
C
练习3:
(4) ( )
(3) ( )
(2) ( )
(1) ( )
A
B
D
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
2.已知∠ACB =∠ADB=90°,要证明 △ABC≌ △BAD,还需一个什么条件? 写出这些条件,并写出判定全等的理由。
A
F
C
E
D
B
3.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF。
求证:BF=DE
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE.
证明:
AB=CD
∴Rt△ABF≌ Rt △CDE
∴ BF=DE
AF=CE
(HL).
(全等三角形对应边相等).
(已证)
(已知)
在Rt△ABF和Rt△CDE中,
∵BF⊥AC,DE⊥AC,
∴∠BFA和∠DEC都是直角.
1.如图,已知∠B=∠E =90°,AB=DE,AC=DF,则判定△ABC≌△DEF的依据是( ).
A.SAS B.ASA C.AAS D.HL
D
A
B
C
D
E
F
巩固新知
2.如图,已知∠C=∠D =90°. 若要根据“HL”判定△ABC≌△ABD,则还需添加的条件是( ).
A.∠BAC=∠BAD
B.∠ABC=∠ABD
C.AC=AD
D.AB=AB
C
A
B
C
D
3.下列条件中,不能判定两个直角三角形全等的是( ).
A.一个锐角和斜边分别相等
B.两条直角边分别相等
C.两个锐角分别相等
D.斜边和一条直角边分别相等
C
4.如图,BE ,CD是△ABC的高,则判定△BCD≌△CBE的依据是( ).
A.SAS B.ASA C. HL D. SSS
C
A
B
C
D
E
5.如图,在Rt△ABC中, ∠ BAC=90°,DE ⊥ BC于点E,AC=EC, ∠ ACB=60°,则∠ ACD度数是( ).
A.45° B.30° C. 20° D. 15°
B
A
B
C
D
E
6.如图,在△ABC中, AB=AC,AE是经过点A的一条直线,且B,C在AE的两侧,BD ⊥ AE于点D, CE ⊥ AE于点E,AD=CE,则∠ BAC度数是( ).
A.45° B.60° C. 90° D. 120°
C
C
A
B
D
E
7.如图,在Rt△ABC中,∠ACB=90°,
E是AB上一点,且BE=BC,DE⊥AB于E,
若AC=8,则AD + DE等于( ).
A.7 B.8 C.9 D.10
A
B
C
D
E
C
8. 如图,有一个直角△ABC,∠C=90°,AC=12,BC=5,一条线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AX上运动,
当AP= 时,才能使△ABC≌△PQA.
C
B
P
Q
A
x
X
5
9. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于 D,DE⊥AB于E,
且AB=6 cm,则△DEB的周长为_____cm.
A
B
C
D
E
6
今天作业
课本P44页第6、7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
