12.2三角形全等的判定(6)课件(共22张PPT)
文档属性
| 名称 | 12.2三角形全等的判定(6)课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
12.2三角形全等的判定 (6)
人教版 八年级上册
全等三角形的性质:
复习旧知
全等三角形的对应边相等.
全等三角形的对应角相等.
常利用全等三角形证明有关的线段或角相等
全等三角形的判定方法
一般三角形:
SSS
SAS
ASA
AAS
直角三角形:
HL
SAS
ASA
AAS
判定两个三角形全等的条件中至少有一组边对应相等.
结论:
全等判定三条件,总得有边方实现.
三边对等最易找,两边一角需夹角.
两角一边任意边,角角边或角边角..
复习旧知
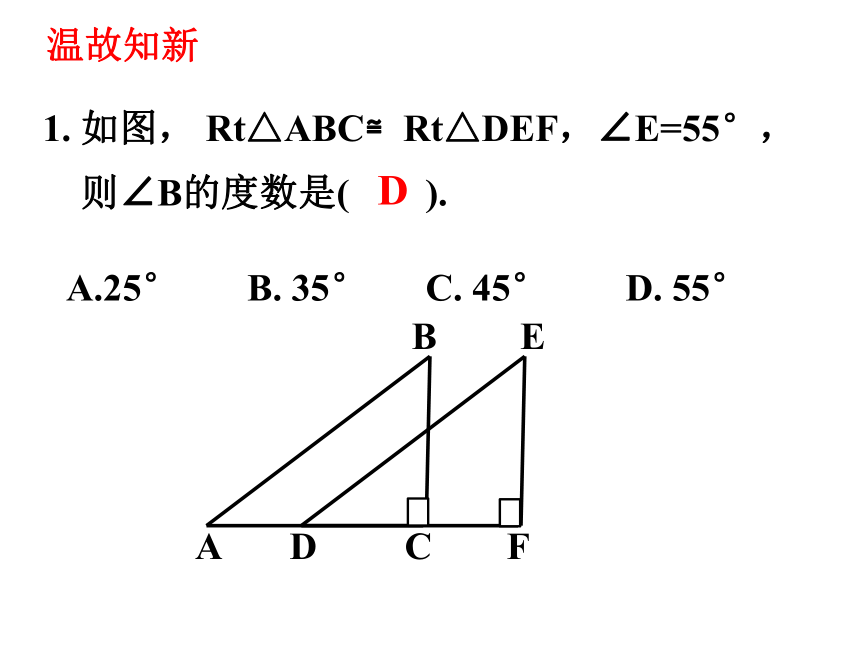
1. 如图, Rt△ABC≌Rt△DEF,∠E=55°,
则∠B的度数是( ).
A.25° B. 35° C. 45° D. 55°
温故知新
B
A
C
E
D
F
D
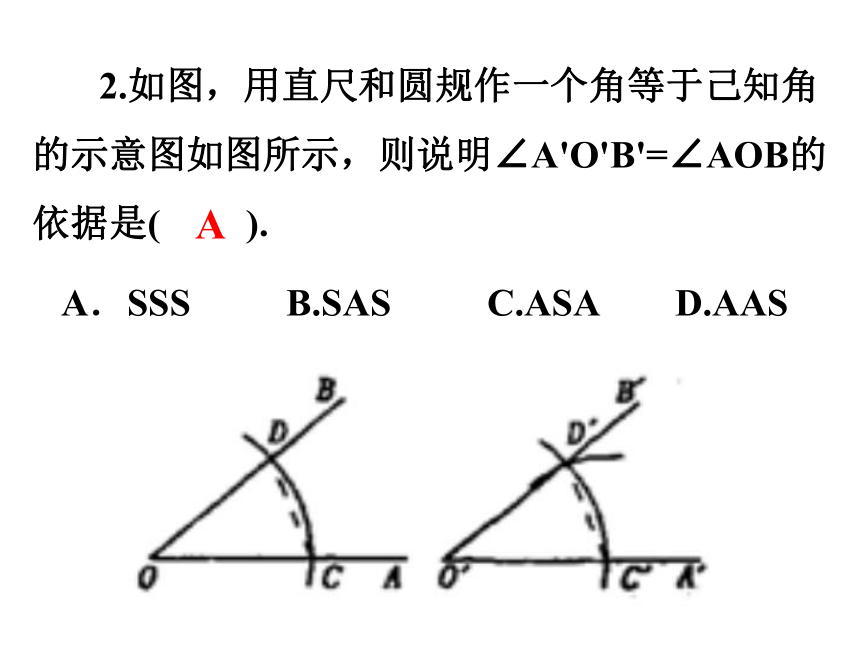
2.如图,用直尺和圆规作一个角等于己知角的示意图如图所示,则说明∠A'O'B'=∠AOB的依据是( ).
A.SSS B.SAS C.ASA D.AAS
A
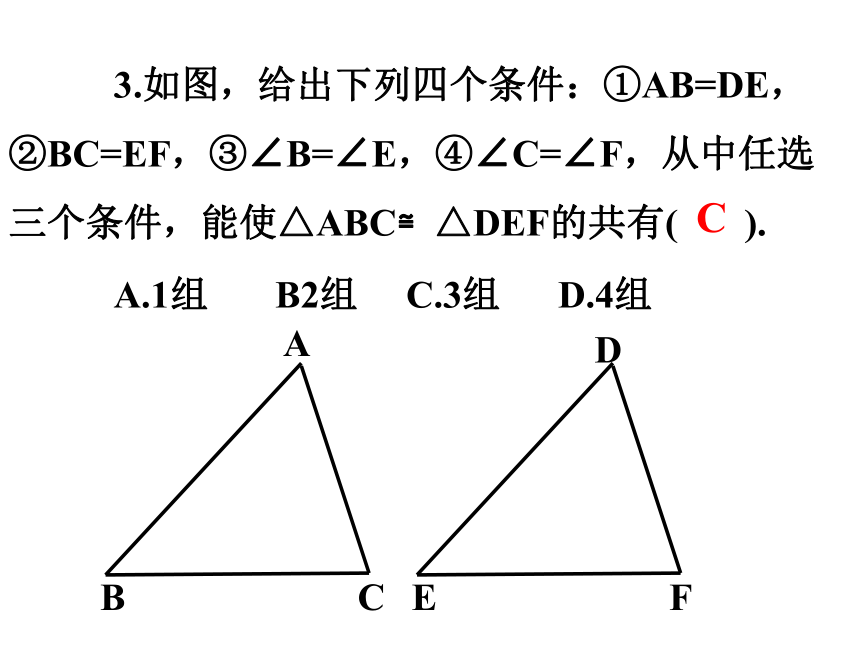
3.如图,给出下列四个条件:①AB=DE,
②BC=EF,③∠B=∠E,④∠C=∠F,从中任选三个条件,能使△ABC≌△DEF的共有( ).
A.1组 B2组 C.3组 D.4组
B
A
C
E
D
F
C
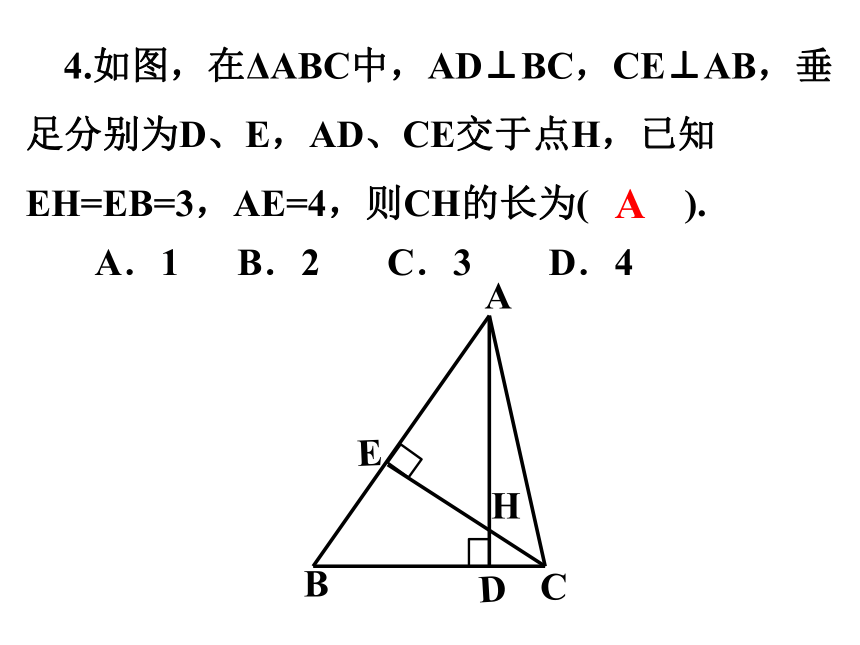
4.如图,在ΔABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长为( ).
A.1 B.2 C.3 D.4
E
B
D
A
C
H
A
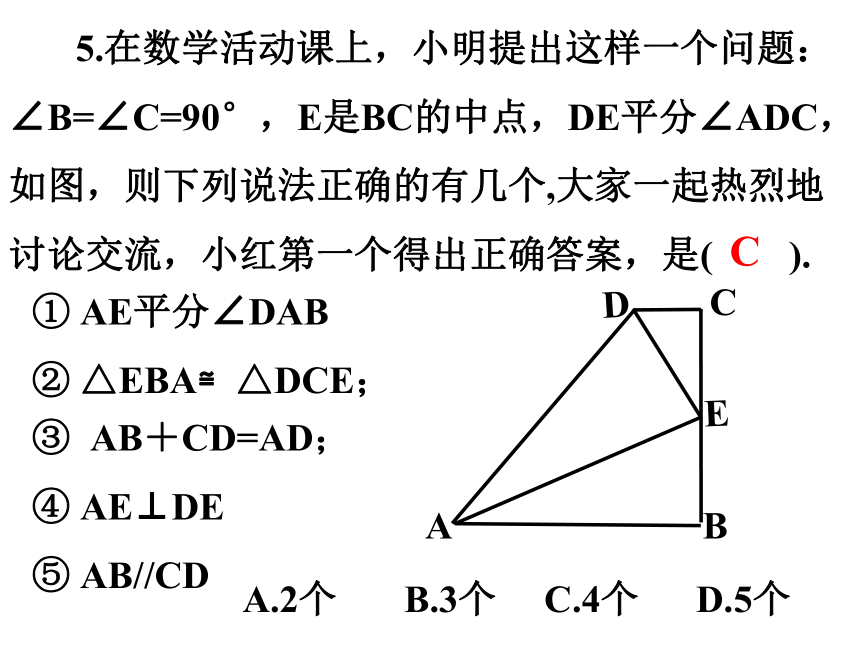
5.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个,大家一起热烈地
讨论交流,小红第一个得出正确答案,是( ).
① AE平分∠DAB
② △EBA≌△DCE;
③ AB+CD=AD;
④ AE⊥DE
⑤ AB//CD
A.2个 B.3个 C.4个 D.5个
E
B
D
A
C
C
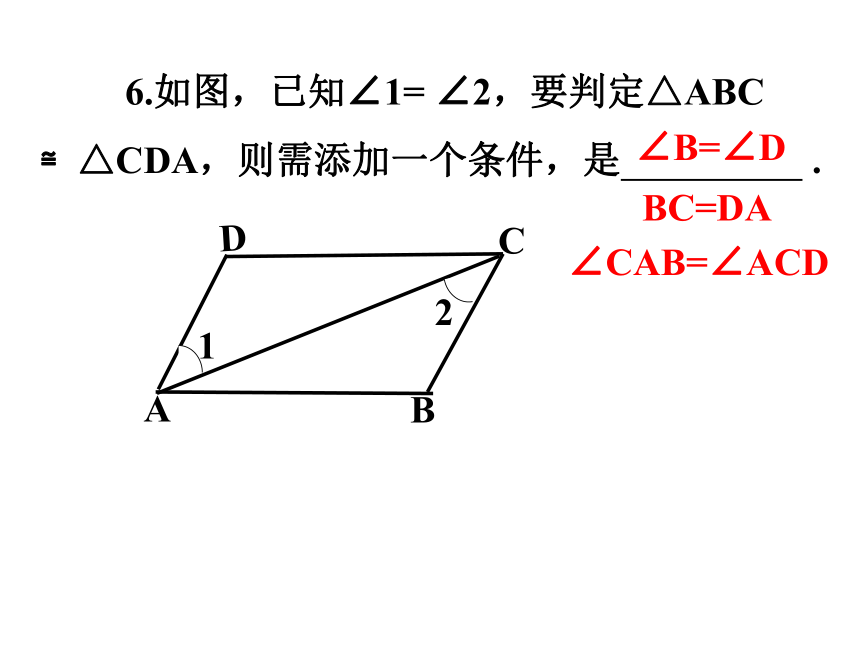
6.如图,已知∠1= ∠2,要判定△ABC
≌△CDA,则需添加一个条件,是 .
B
D
A
C
1
2
∠B=∠D
BC=DA
∠CAB=∠ACD
7.如图,已知AB=DC,∠ABC=∠DCB.
要证 OB=OC,可以先依据“SAS”判定
,得到∠A=∠D,在依据“_________”证判定△AOB≌ ,得到OB=OC.
A
B
C
D
O
AAS
△ABC≌△DCB
△DOC
例1.如图, AB ∥ CD,AE⊥BD于点E,CF⊥
BD于点F,BF=DE. △ABE≌△CDF.
典型例析
B
D
A
C
1
2
E
F
△ABE≌△CDF
BE=DF
∠AEB=∠CFD
AE⊥BD
CF⊥BD
BF=DE
要证:
例1.如图, AB ∥ CD,AE⊥BD于点E,CF⊥
BD于点F,BF=DE. △ABE≌△CDF.
B
D
A
C
1
2
E
F
∴ △ABE≌△CDF
∴ BE=DF.
∴∠AEB=∠CFD=90°.
∵ AE⊥BD,
CF⊥BD,
∵ BF=DE,
证明:
∵ AB ∥ CD,
∴ ∠1=∠2
∴ BF - EF=DE - EF,
在△ABE与△CDF中
(AAS).
∠1=∠2
∠AEB=∠CFD
BE=DF
例2.如图,已知AB=AC, ∠B=∠C. BE与CD相交于点O.求证:OB=OC.
A
B
C
D
E
O
要证:
OB=OC
△BOD≌△COE
BD=CE
AD=AE
△ABE≌△ACD
要证两次三角形全等
例2.如图,已知AB=AC, ∠B=∠C. BE与CD相交于点O.求证:OB=OC.
A
B
C
D
E
O
∴ BD=CE.
∴ AD=AE.
∴△ABE≌△ACD
证明:
在△ABE与△ACD中
∠B=∠C
AB=AC
∠A=∠A
(SAS).
∴AB- AD=AC-AE,
A
B
C
D
E
O
∴ △BOD≌△COE.
∴ BD=CE.
∴ AD=AE.
∴△ABE≌△ACD
证明:
在△ABE与△ACD中
∠B=∠C
AB=AC
∴ OB=OC.
∠A=∠A
(SAS).
∴AB- AD=AC-AE,
(ASA).
在△BOD与△COE中
∠B=∠C
BD=GE
∠BOD=∠COE
1.如图,已知点B、E、F、C在同一直线上AB=DC, BE=CF,∠B=∠C, OE=OF.求证:OA=OD.
∴ BF=CE.
∵ BE=CF,
∴△ABF≌△DCE
证明:
在△ABF与△DCE中
∠B=∠C
AB=DC
BF=CE
(SAS).
∴BE+EF=CF+EF,
A
B
C
D
E
O
F
∴ AF=DE.
∵ OE=OF,
∴AF-OF=DE-OE,
∴ OA=OD.
巩固提高
2.如图,在ΔABC中,AD平分∠BAC,DE⊥
AB,DF⊥AC,垂足分别为E、F,且BD=CD,求证:BE=CF.
A
B
C
D
E
F
AD平分∠BAC
DE⊥AB,DF⊥AC
要证:
∠AED=∠AFD=90°
∠BAD=∠CAD
DE=DF
∴△AED≌△AFD
BE=CF.
∴ Rt△BDE ≌ Rt△CDF
2.如图,在ΔABC中,AD平分∠BAC,DE⊥
AB,DF⊥AC,垂足分别为E、F,且BD=CD,求证:BE=CF.
A
B
C
D
E
F
∵ AD平分∠BAC,
∵ DE⊥AB,DF⊥AC,
∴ ∠BAD=∠CAD.
证明:
∴∠AED=∠AFD=90°.
在△AED与△AFD中
∠BAD=∠CAD
AB=AC
∠AED=∠AFD
∴△AED≌△AFD
(AAS).
∴ DE=DF.
A
B
C
D
E
F
∵ AD平分∠BAC,
∵ DE⊥AB,DF⊥AC,
∴ ∠BAD=∠CAD.
证明:
∴∠AED=∠AFD=90°.
在△AED与△AFD中
∠BAD=∠CAD
AB=AC
∠AED=∠AFD
∴△AED≌△AFD
(AAS).
∴ DE=DF.
在Rt△BDE和Rt△CDF中
DE=DF
BD=CD
∴BE=CF.
∴ Rt△BDE ≌ Rt△CDF
(HL).
今天作业
课本P44页第4、5、11题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.2三角形全等的判定 (6)
人教版 八年级上册
全等三角形的性质:
复习旧知
全等三角形的对应边相等.
全等三角形的对应角相等.
常利用全等三角形证明有关的线段或角相等
全等三角形的判定方法
一般三角形:
SSS
SAS
ASA
AAS
直角三角形:
HL
SAS
ASA
AAS
判定两个三角形全等的条件中至少有一组边对应相等.
结论:
全等判定三条件,总得有边方实现.
三边对等最易找,两边一角需夹角.
两角一边任意边,角角边或角边角..
复习旧知
1. 如图, Rt△ABC≌Rt△DEF,∠E=55°,
则∠B的度数是( ).
A.25° B. 35° C. 45° D. 55°
温故知新
B
A
C
E
D
F
D
2.如图,用直尺和圆规作一个角等于己知角的示意图如图所示,则说明∠A'O'B'=∠AOB的依据是( ).
A.SSS B.SAS C.ASA D.AAS
A
3.如图,给出下列四个条件:①AB=DE,
②BC=EF,③∠B=∠E,④∠C=∠F,从中任选三个条件,能使△ABC≌△DEF的共有( ).
A.1组 B2组 C.3组 D.4组
B
A
C
E
D
F
C
4.如图,在ΔABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长为( ).
A.1 B.2 C.3 D.4
E
B
D
A
C
H
A
5.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个,大家一起热烈地
讨论交流,小红第一个得出正确答案,是( ).
① AE平分∠DAB
② △EBA≌△DCE;
③ AB+CD=AD;
④ AE⊥DE
⑤ AB//CD
A.2个 B.3个 C.4个 D.5个
E
B
D
A
C
C
6.如图,已知∠1= ∠2,要判定△ABC
≌△CDA,则需添加一个条件,是 .
B
D
A
C
1
2
∠B=∠D
BC=DA
∠CAB=∠ACD
7.如图,已知AB=DC,∠ABC=∠DCB.
要证 OB=OC,可以先依据“SAS”判定
,得到∠A=∠D,在依据“_________”证判定△AOB≌ ,得到OB=OC.
A
B
C
D
O
AAS
△ABC≌△DCB
△DOC
例1.如图, AB ∥ CD,AE⊥BD于点E,CF⊥
BD于点F,BF=DE. △ABE≌△CDF.
典型例析
B
D
A
C
1
2
E
F
△ABE≌△CDF
BE=DF
∠AEB=∠CFD
AE⊥BD
CF⊥BD
BF=DE
要证:
例1.如图, AB ∥ CD,AE⊥BD于点E,CF⊥
BD于点F,BF=DE. △ABE≌△CDF.
B
D
A
C
1
2
E
F
∴ △ABE≌△CDF
∴ BE=DF.
∴∠AEB=∠CFD=90°.
∵ AE⊥BD,
CF⊥BD,
∵ BF=DE,
证明:
∵ AB ∥ CD,
∴ ∠1=∠2
∴ BF - EF=DE - EF,
在△ABE与△CDF中
(AAS).
∠1=∠2
∠AEB=∠CFD
BE=DF
例2.如图,已知AB=AC, ∠B=∠C. BE与CD相交于点O.求证:OB=OC.
A
B
C
D
E
O
要证:
OB=OC
△BOD≌△COE
BD=CE
AD=AE
△ABE≌△ACD
要证两次三角形全等
例2.如图,已知AB=AC, ∠B=∠C. BE与CD相交于点O.求证:OB=OC.
A
B
C
D
E
O
∴ BD=CE.
∴ AD=AE.
∴△ABE≌△ACD
证明:
在△ABE与△ACD中
∠B=∠C
AB=AC
∠A=∠A
(SAS).
∴AB- AD=AC-AE,
A
B
C
D
E
O
∴ △BOD≌△COE.
∴ BD=CE.
∴ AD=AE.
∴△ABE≌△ACD
证明:
在△ABE与△ACD中
∠B=∠C
AB=AC
∴ OB=OC.
∠A=∠A
(SAS).
∴AB- AD=AC-AE,
(ASA).
在△BOD与△COE中
∠B=∠C
BD=GE
∠BOD=∠COE
1.如图,已知点B、E、F、C在同一直线上AB=DC, BE=CF,∠B=∠C, OE=OF.求证:OA=OD.
∴ BF=CE.
∵ BE=CF,
∴△ABF≌△DCE
证明:
在△ABF与△DCE中
∠B=∠C
AB=DC
BF=CE
(SAS).
∴BE+EF=CF+EF,
A
B
C
D
E
O
F
∴ AF=DE.
∵ OE=OF,
∴AF-OF=DE-OE,
∴ OA=OD.
巩固提高
2.如图,在ΔABC中,AD平分∠BAC,DE⊥
AB,DF⊥AC,垂足分别为E、F,且BD=CD,求证:BE=CF.
A
B
C
D
E
F
AD平分∠BAC
DE⊥AB,DF⊥AC
要证:
∠AED=∠AFD=90°
∠BAD=∠CAD
DE=DF
∴△AED≌△AFD
BE=CF.
∴ Rt△BDE ≌ Rt△CDF
2.如图,在ΔABC中,AD平分∠BAC,DE⊥
AB,DF⊥AC,垂足分别为E、F,且BD=CD,求证:BE=CF.
A
B
C
D
E
F
∵ AD平分∠BAC,
∵ DE⊥AB,DF⊥AC,
∴ ∠BAD=∠CAD.
证明:
∴∠AED=∠AFD=90°.
在△AED与△AFD中
∠BAD=∠CAD
AB=AC
∠AED=∠AFD
∴△AED≌△AFD
(AAS).
∴ DE=DF.
A
B
C
D
E
F
∵ AD平分∠BAC,
∵ DE⊥AB,DF⊥AC,
∴ ∠BAD=∠CAD.
证明:
∴∠AED=∠AFD=90°.
在△AED与△AFD中
∠BAD=∠CAD
AB=AC
∠AED=∠AFD
∴△AED≌△AFD
(AAS).
∴ DE=DF.
在Rt△BDE和Rt△CDF中
DE=DF
BD=CD
∴BE=CF.
∴ Rt△BDE ≌ Rt△CDF
(HL).
今天作业
课本P44页第4、5、11题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
