第12章全等三角形小结 课件(共27张PPT)
文档属性
| 名称 | 第12章全等三角形小结 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 06:30:38 | ||
图片预览



文档简介
(共27张PPT)
第12章 全等三角形 小结
人教版 八年级上册
全等三角形的性质:
复习旧知
全等三角形的对应边相等.
全等三角形的对应角相等.
常利用全等三角形证明有关的线段或角相等
全等三角形的判定方法
一般三角形:
SSS
SAS
ASA
AAS
直角三角形:
HL
SAS
ASA
AAS
判定两个三角形全等的条件中至少有一组边对应相等.
结论:
全等判定三条件,总得有边方实现.
三边对等最易找,两边一角需夹角.
两角一边任意边,角角边或角边角..
复习旧知
两个三角形有一组边
对应相等吗
还有另外一组
边对应相等吗
第三组边也
对应相等吗
夹相等对应边的角中
有一组角对应相等吗
夹相等对应边的角中
另一组角对也应相等吗
相等对应边的对角相等吗
对应相等两边的
夹角相等吗
否
是
是
是
否
是
对应相等两边中一边
所对的角是直角吗
是
满足SSS
全等
满足SAS
全等
全等
满足ASA
满足AAS
全等
满足HL
全等
否
是
是
否
是
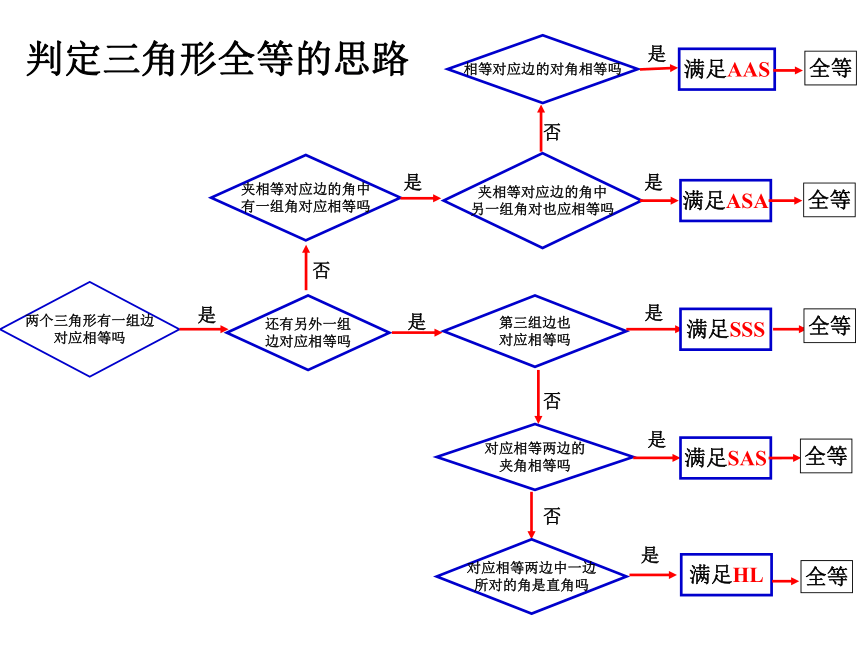
判定三角形全等的思路
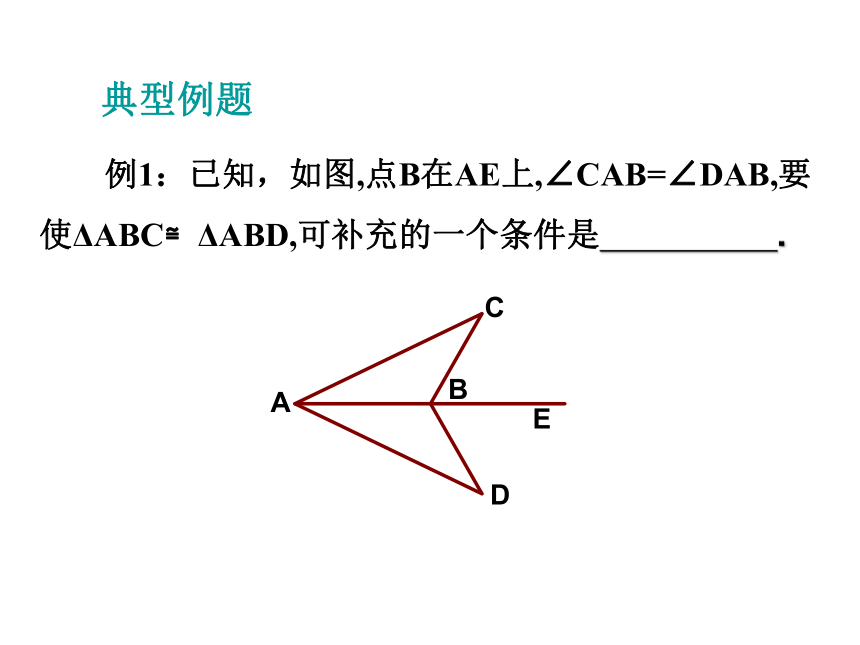
例1:已知,如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .
典型例题
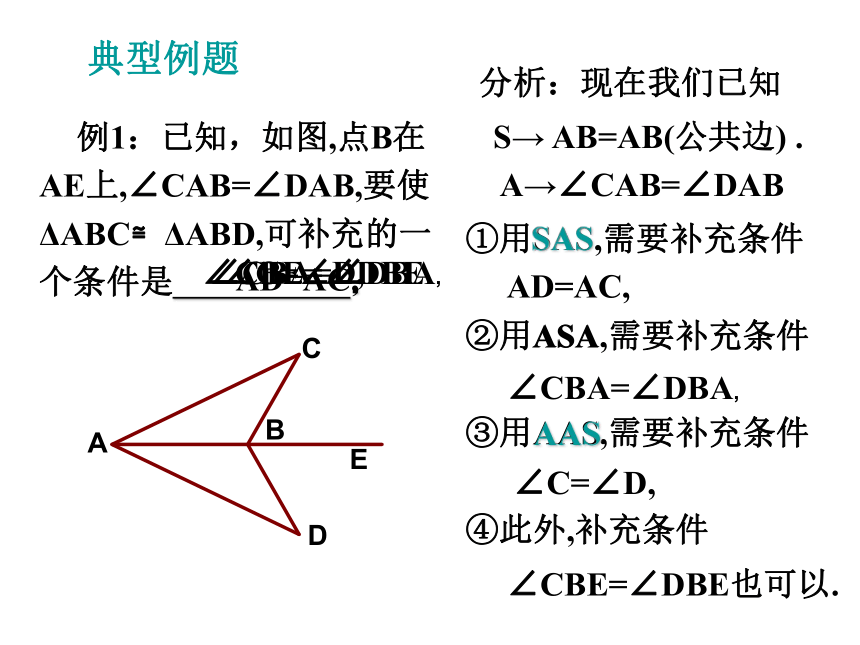
例1:已知,如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .
分析:现在我们已知
①用SAS,需要补充条件
②用ASA,需要补充条件
③用AAS,需要补充条件
④此外,补充条件
SAS
ASA
AAS
A→∠CAB=∠DAB
S→ AB=AB(公共边) .
典型例题
AD=AC,
∠CBA=∠DBA,
∠C=∠D,
∠CBE=∠DBE也可以.
AD=AC,
∠CBA=∠DBA,
∠C=∠D,
∠CBE=∠DBE
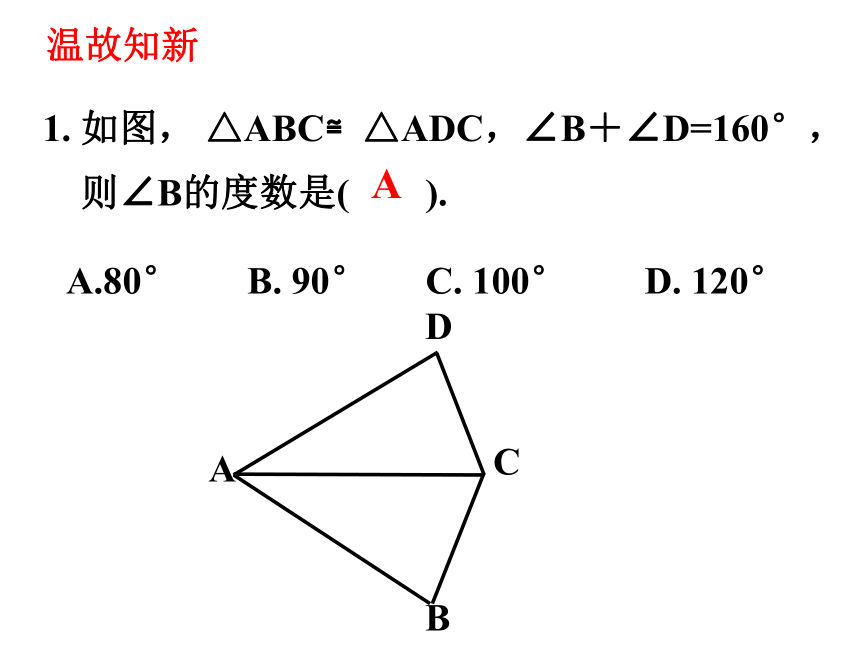
1. 如图, △ABC≌△ADC,∠B+∠D=160°,
则∠B的度数是( ).
A.80° B. 90° C. 100° D. 120°
温故知新
B
A
C
D
A
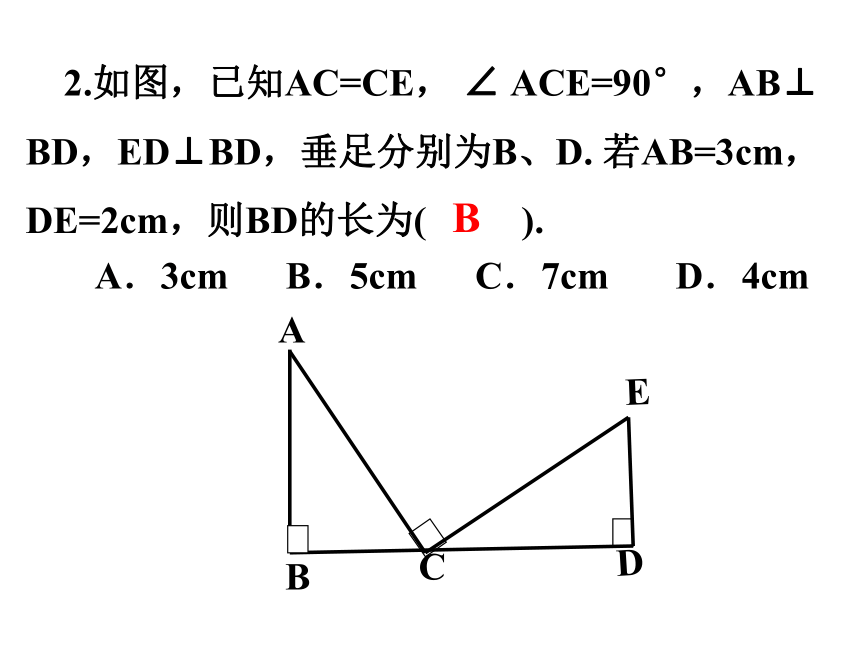
2.如图,已知AC=CE, ∠ ACE=90°,AB⊥
BD,ED⊥BD,垂足分别为B、D. 若AB=3cm,DE=2cm,则BD的长为( ).
A.3cm B.5cm C.7cm D.4cm
B
E
B
D
A
C
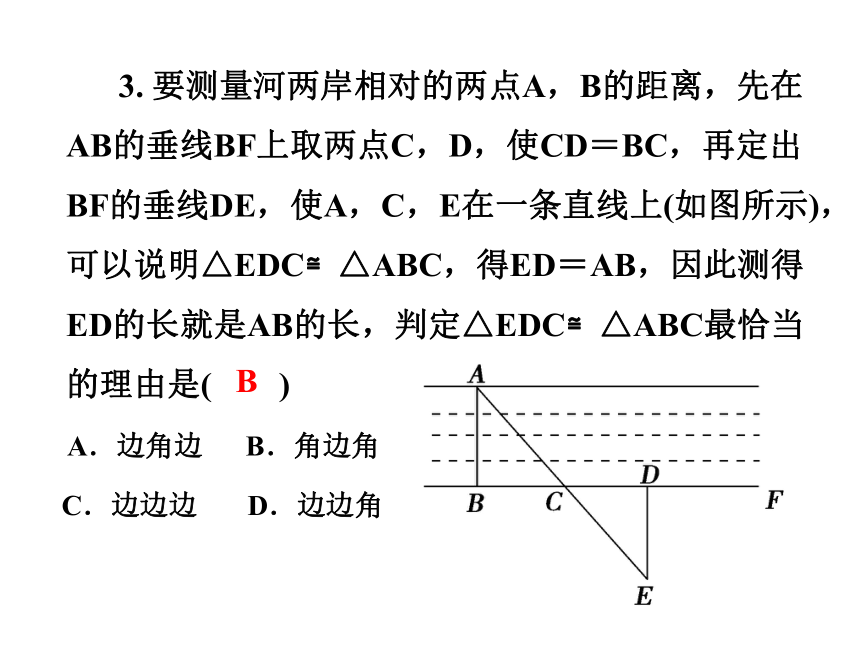
3. 要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
A.边角边 B.角边角
C.边边边 D.边边角
B
4. 如图,已知AC=AD,∠1=∠2, 增加下列条件: ①AB=AE, ②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个.
A.4 B.3 C.2 D.1
B
5.如图,在△ABC和△DEC中,已知AB=DE,还需要添加两个条件才能使△ABC≌△DEC,不能添加的一组是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
C
6. 如图, 已知AB=CB,AD=CD.若∠A=108°,
BC=6,则∠C的度数是 ,AB= .
B
A
C
D
6
108°
7. 如图,已知,AE=AD,要使ΔABD≌ΔACE,请你增加一个条件是 .
AB=AC,
∠B=∠C,
∠BDA =∠CEA,
∠CDB=∠BEC,
8.如图,已知 AB⊥BD,ED⊥BD,垂足分别为B、D. AB=CD,AC=CE,则∠ACE= .
90°
E
B
D
A
C
9.如图,在2 × 2的方格中,连接 AB,AC,
则△AMC≌ ;∠1 + ∠2= .
90°
△ANB
2
N
B
M
A
C
1
10. 如图,已知∠E=∠F=90°∠B=∠C, AE=AF.有下列结论: ①EM=FN, ②CD=DN,③∠1=∠2,④ △ACN≌△ABM,其中正确的结论有 (填序号 ).
①
B
A
E
F
C
M
N
1
2
D
③
④
例2已知,如图,在 ΔABC中,AD⊥BC于D,
BE⊥AC于E,AD交BE于F,若BF=AC.
求证:AD=BD.
AD⊥BC,BE⊥AC
ΔBFD≌ΔACD
AD=BD
∠1=∠2.
∠BDA=∠ADC=∠BEC= 90°
1
2
要证:
例2已知,如图,在 ΔABC中,AD⊥BC于D,BE⊥AC于E,AD交BE于F,若BF=AC. 求证:AD=BD.
∵AD⊥BC,BE⊥AC,
∴ΔBFD≌ΔACD
∴ AD=BD.
∴ ∠1=∠2.
BF=AC
∠2 + ∠C= 90°,
∴ ∠1 + ∠C= 90°,
∴∠BDA=∠ADC=∠BEC= 90°
在△BFD和△ACD中,
∠BDF=∠ADC
∠1=∠2
1
2
证明:
(AAS)
8.如图,已知:AB=AC,DB=DC,F是AD的
延长线上的点.
A
B
C
D
F
求证:BF=CF.
△ABC≌△ACD
∠BAD=∠CAD.
△ABF≌△ACF
BF=CF.
要证:
例3.如图,已知:AB=AC,DB=DC,F是AD的
延长线上的点.
A
B
C
D
F
求证:BF=CF.
在△ABD和△ACD中,
AB=AC
AD=AD
∴ △ABC≌△ACD
∴ ∠BAD=∠CAD.
BD=CD
证明:
A
B
C
D
F
在△ABD和△ACD中,
AB=AC
AD=AD
∴ △ABC≌△ACD
∴ ∠BAD=∠CAD.
BD=CD
在△ABF和△ACF中,
AB=DC
∠BAF=∠CAF
∴ △ABF≌△ACF
∴BF=CF.
AF=AF
证明:
(SSS)
(SAS)
8.如图,已知:AB=AC,DB=DC,F是AD的
延长线上的点.
求证:BF=CF.
A
B
C
D
F
∵ AB=AC,
∴点A在BC的垂直平分线上.
∵ DB=DC,
∴点D在BC的垂直平分线上.
∴AD是BC的垂直平分线。
证明:
∴BF=CF.
例4.如图,已知:AB=AD, BC=DC,E、F
分别是BC、DC的中点. 求证:AE=AF.
A
B
C
E
D
F
△ABC≌△ACD
∠D=∠B.
△ADE≌△ABF
AE=AF.
要证:
A
B
C
E
D
F
证明:
∴△ABC≌△ADC
∴BF=DE.
∴ ∠B=∠D.
连接AC
在△ABC和△ADC中,
AB=AD
BC=DC
AC=AC
∵BF= BC,
(SSS)
DE= DC,
在△ABF 和△AED中,
AB=AD
∠B=∠D
BF=DE
∴△ABF≌△ADE
∴AE=AF.
1
2
1
2
例4.如图,已知:AB=AD, BC=DC,E、F
分别是BC、DC的中点. 求证:AE=AF.
今天作业
课本P55页第3题
课本P56页第8、9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第12章 全等三角形 小结
人教版 八年级上册
全等三角形的性质:
复习旧知
全等三角形的对应边相等.
全等三角形的对应角相等.
常利用全等三角形证明有关的线段或角相等
全等三角形的判定方法
一般三角形:
SSS
SAS
ASA
AAS
直角三角形:
HL
SAS
ASA
AAS
判定两个三角形全等的条件中至少有一组边对应相等.
结论:
全等判定三条件,总得有边方实现.
三边对等最易找,两边一角需夹角.
两角一边任意边,角角边或角边角..
复习旧知
两个三角形有一组边
对应相等吗
还有另外一组
边对应相等吗
第三组边也
对应相等吗
夹相等对应边的角中
有一组角对应相等吗
夹相等对应边的角中
另一组角对也应相等吗
相等对应边的对角相等吗
对应相等两边的
夹角相等吗
否
是
是
是
否
是
对应相等两边中一边
所对的角是直角吗
是
满足SSS
全等
满足SAS
全等
全等
满足ASA
满足AAS
全等
满足HL
全等
否
是
是
否
是
判定三角形全等的思路
例1:已知,如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .
典型例题
例1:已知,如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .
分析:现在我们已知
①用SAS,需要补充条件
②用ASA,需要补充条件
③用AAS,需要补充条件
④此外,补充条件
SAS
ASA
AAS
A→∠CAB=∠DAB
S→ AB=AB(公共边) .
典型例题
AD=AC,
∠CBA=∠DBA,
∠C=∠D,
∠CBE=∠DBE也可以.
AD=AC,
∠CBA=∠DBA,
∠C=∠D,
∠CBE=∠DBE
1. 如图, △ABC≌△ADC,∠B+∠D=160°,
则∠B的度数是( ).
A.80° B. 90° C. 100° D. 120°
温故知新
B
A
C
D
A
2.如图,已知AC=CE, ∠ ACE=90°,AB⊥
BD,ED⊥BD,垂足分别为B、D. 若AB=3cm,DE=2cm,则BD的长为( ).
A.3cm B.5cm C.7cm D.4cm
B
E
B
D
A
C
3. 要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
A.边角边 B.角边角
C.边边边 D.边边角
B
4. 如图,已知AC=AD,∠1=∠2, 增加下列条件: ①AB=AE, ②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个.
A.4 B.3 C.2 D.1
B
5.如图,在△ABC和△DEC中,已知AB=DE,还需要添加两个条件才能使△ABC≌△DEC,不能添加的一组是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
C
6. 如图, 已知AB=CB,AD=CD.若∠A=108°,
BC=6,则∠C的度数是 ,AB= .
B
A
C
D
6
108°
7. 如图,已知,AE=AD,要使ΔABD≌ΔACE,请你增加一个条件是 .
AB=AC,
∠B=∠C,
∠BDA =∠CEA,
∠CDB=∠BEC,
8.如图,已知 AB⊥BD,ED⊥BD,垂足分别为B、D. AB=CD,AC=CE,则∠ACE= .
90°
E
B
D
A
C
9.如图,在2 × 2的方格中,连接 AB,AC,
则△AMC≌ ;∠1 + ∠2= .
90°
△ANB
2
N
B
M
A
C
1
10. 如图,已知∠E=∠F=90°∠B=∠C, AE=AF.有下列结论: ①EM=FN, ②CD=DN,③∠1=∠2,④ △ACN≌△ABM,其中正确的结论有 (填序号 ).
①
B
A
E
F
C
M
N
1
2
D
③
④
例2已知,如图,在 ΔABC中,AD⊥BC于D,
BE⊥AC于E,AD交BE于F,若BF=AC.
求证:AD=BD.
AD⊥BC,BE⊥AC
ΔBFD≌ΔACD
AD=BD
∠1=∠2.
∠BDA=∠ADC=∠BEC= 90°
1
2
要证:
例2已知,如图,在 ΔABC中,AD⊥BC于D,BE⊥AC于E,AD交BE于F,若BF=AC. 求证:AD=BD.
∵AD⊥BC,BE⊥AC,
∴ΔBFD≌ΔACD
∴ AD=BD.
∴ ∠1=∠2.
BF=AC
∠2 + ∠C= 90°,
∴ ∠1 + ∠C= 90°,
∴∠BDA=∠ADC=∠BEC= 90°
在△BFD和△ACD中,
∠BDF=∠ADC
∠1=∠2
1
2
证明:
(AAS)
8.如图,已知:AB=AC,DB=DC,F是AD的
延长线上的点.
A
B
C
D
F
求证:BF=CF.
△ABC≌△ACD
∠BAD=∠CAD.
△ABF≌△ACF
BF=CF.
要证:
例3.如图,已知:AB=AC,DB=DC,F是AD的
延长线上的点.
A
B
C
D
F
求证:BF=CF.
在△ABD和△ACD中,
AB=AC
AD=AD
∴ △ABC≌△ACD
∴ ∠BAD=∠CAD.
BD=CD
证明:
A
B
C
D
F
在△ABD和△ACD中,
AB=AC
AD=AD
∴ △ABC≌△ACD
∴ ∠BAD=∠CAD.
BD=CD
在△ABF和△ACF中,
AB=DC
∠BAF=∠CAF
∴ △ABF≌△ACF
∴BF=CF.
AF=AF
证明:
(SSS)
(SAS)
8.如图,已知:AB=AC,DB=DC,F是AD的
延长线上的点.
求证:BF=CF.
A
B
C
D
F
∵ AB=AC,
∴点A在BC的垂直平分线上.
∵ DB=DC,
∴点D在BC的垂直平分线上.
∴AD是BC的垂直平分线。
证明:
∴BF=CF.
例4.如图,已知:AB=AD, BC=DC,E、F
分别是BC、DC的中点. 求证:AE=AF.
A
B
C
E
D
F
△ABC≌△ACD
∠D=∠B.
△ADE≌△ABF
AE=AF.
要证:
A
B
C
E
D
F
证明:
∴△ABC≌△ADC
∴BF=DE.
∴ ∠B=∠D.
连接AC
在△ABC和△ADC中,
AB=AD
BC=DC
AC=AC
∵BF= BC,
(SSS)
DE= DC,
在△ABF 和△AED中,
AB=AD
∠B=∠D
BF=DE
∴△ABF≌△ADE
∴AE=AF.
1
2
1
2
例4.如图,已知:AB=AD, BC=DC,E、F
分别是BC、DC的中点. 求证:AE=AF.
今天作业
课本P55页第3题
课本P56页第8、9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
