2022-2023学年人教B版2019必修三7.4 数学建模活动:周期现象的描述 同步课时训练(word版含解析)
文档属性
| 名称 | 2022-2023学年人教B版2019必修三7.4 数学建模活动:周期现象的描述 同步课时训练(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 489.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 00:00:00 | ||
图片预览


文档简介
7.4 数学建模活动:周期现象的描述 同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)电流强度I(安培)随时间t(秒)变化的函数的图象如图所示,则时的电流强度为( )
A.0安培 B.安培 C.安培 D.安培
2、(4分)商场人流量被定义为每分钟通过入口的人数,五一某商场的人流量满足函数,则下列时间段内人流量是增加的是( )
A. B. C. D.
3、(4分)某种商品一年内每件出厂价在7千元的基础上,按月呈的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定的解析式为( )
A.
B.
C.
D.
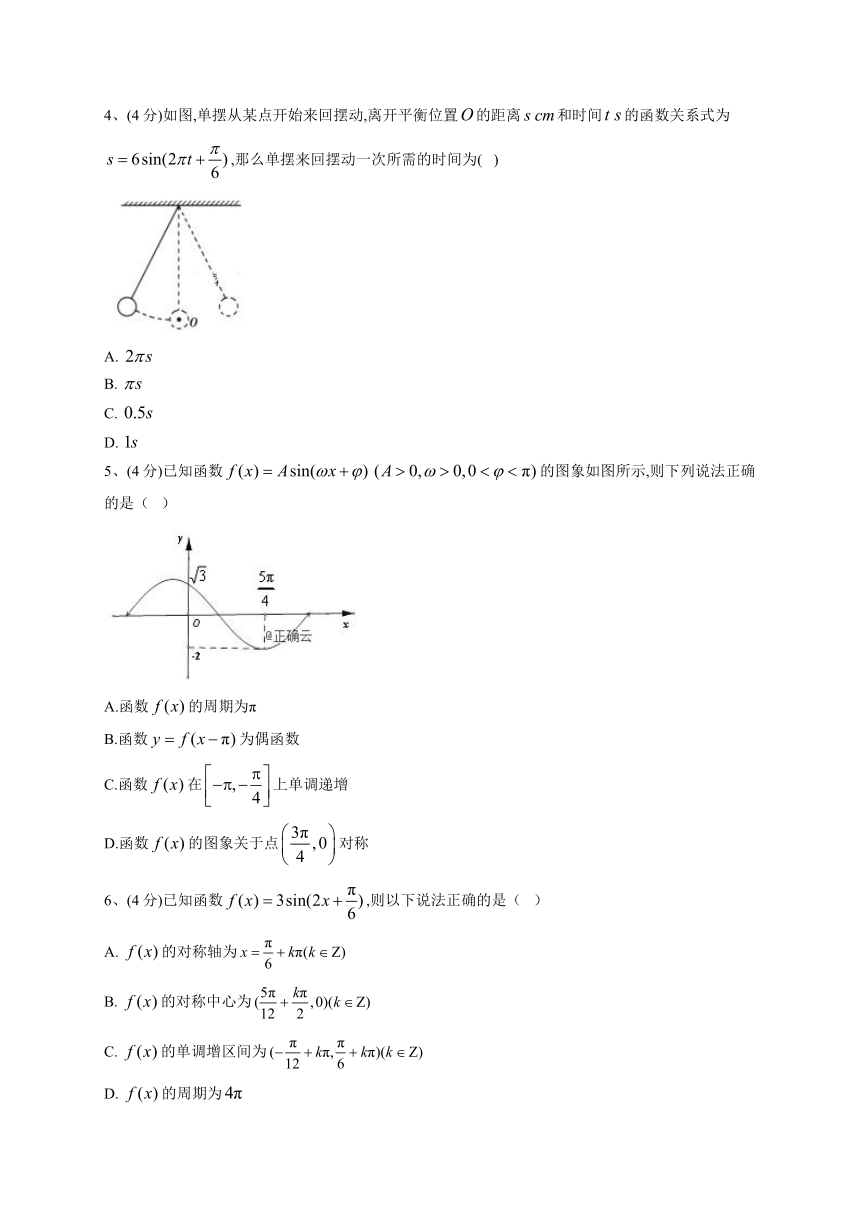
4、(4分)如图,单摆从某点开始来回摆动,离开平衡位置的距离和时间的函数关系式为,那么单摆来回摆动一次所需的时间为( )
A.
B.
C.
D.
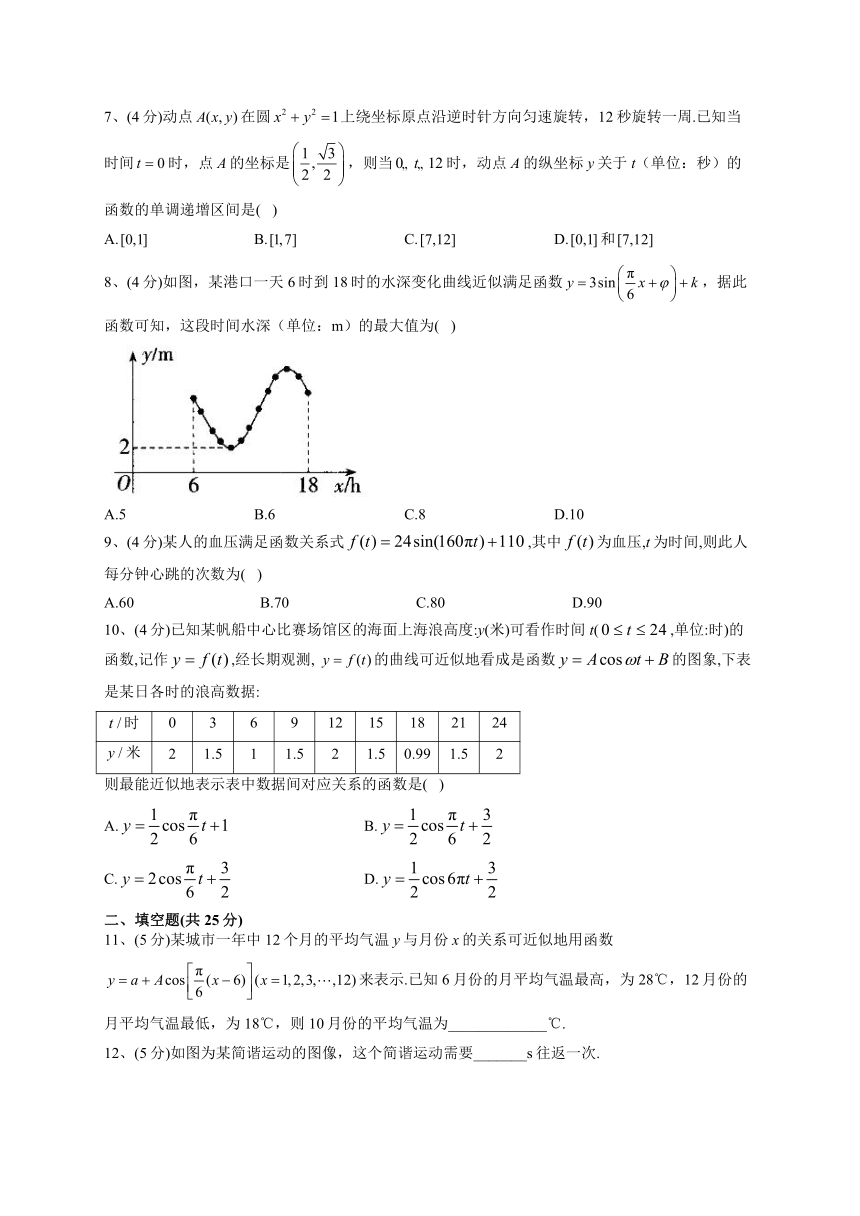
5、(4分)已知函数的图象如图所示,则下列说法正确的是( )
A.函数的周期为π
B.函数为偶函数
C.函数在上单调递增
D.函数的图象关于点对称
6、(4分)已知函数,则以下说法正确的是( )
A. 的对称轴为
B. 的对称中心为
C. 的单调增区间为
D. 的周期为
7、(4分)动点在圆上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知当时间时,点A的坐标是,则当时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A. B. C. D.和
8、(4分)如图,某港口一天6时到18时的水深变化曲线近似满足函数,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
9、(4分)某人的血压满足函数关系式,其中为血压,t为时间,则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
10、(4分)已知某帆船中心比赛场馆区的海面上海浪高度:y(米)可看作时间t(,单位:时)的函数,记作,经长期观测, 的曲线可近似地看成是函数的图象,下表是某日各时的浪高数据:
0 3 6 9 12 15 18 21 24
2 1.5 1 1.5 2 1.5 0.99 1.5 2
则最能近似地表示表中数据间对应关系的函数是( )
A. B.
C. D.
二、填空题(共25分)
11、(5分)某城市一年中12个月的平均气温y与月份x的关系可近似地用函数来表示.已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为_____________℃.
12、(5分)如图为某简谐运动的图像,这个简谐运动需要_______s往返一次.
13、(5分)某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间时,点A与钟面上标12的点B重合,将A,B两点的距离d(cm)表示成t(s)的函数,则________,.
14、(5分)已知的周期为π,则当时的最小值为________
15、(5分)关于函数有下列命题,其中正确的是__________
① 的表达式可改写为;
② 是以为最小正周期的周期函数;
③ 的图象关于点对称;
④ 的图象关于直线对称.
三、解答题(共35分)
16、(8分)已知某海滨浴场的海浪高度y(米)是时间t(,单位:时)的函数,记作,下表是某日某时的浪高数据.
t/时 0 3 6 9 12 15 18 21 24
y/米 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,的曲线可近似地看成是函数.
(1)根据上表数据,求函数的最小正周期T、振幅A及函数解析式.
(2)依据规定,当海浪高度等于或高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内8时至20时之间,有多长时间可供冲浪爱好者进行运动?
17、(9分)已知某地一天从4~16时的温度变化曲线近似满足函数.
(1)求该地区这一段时间内温度的最大温差.
(2)若有一种细菌在15℃到25℃之间可以生存,则在这段时间内,该细菌最多能生存多长时间?
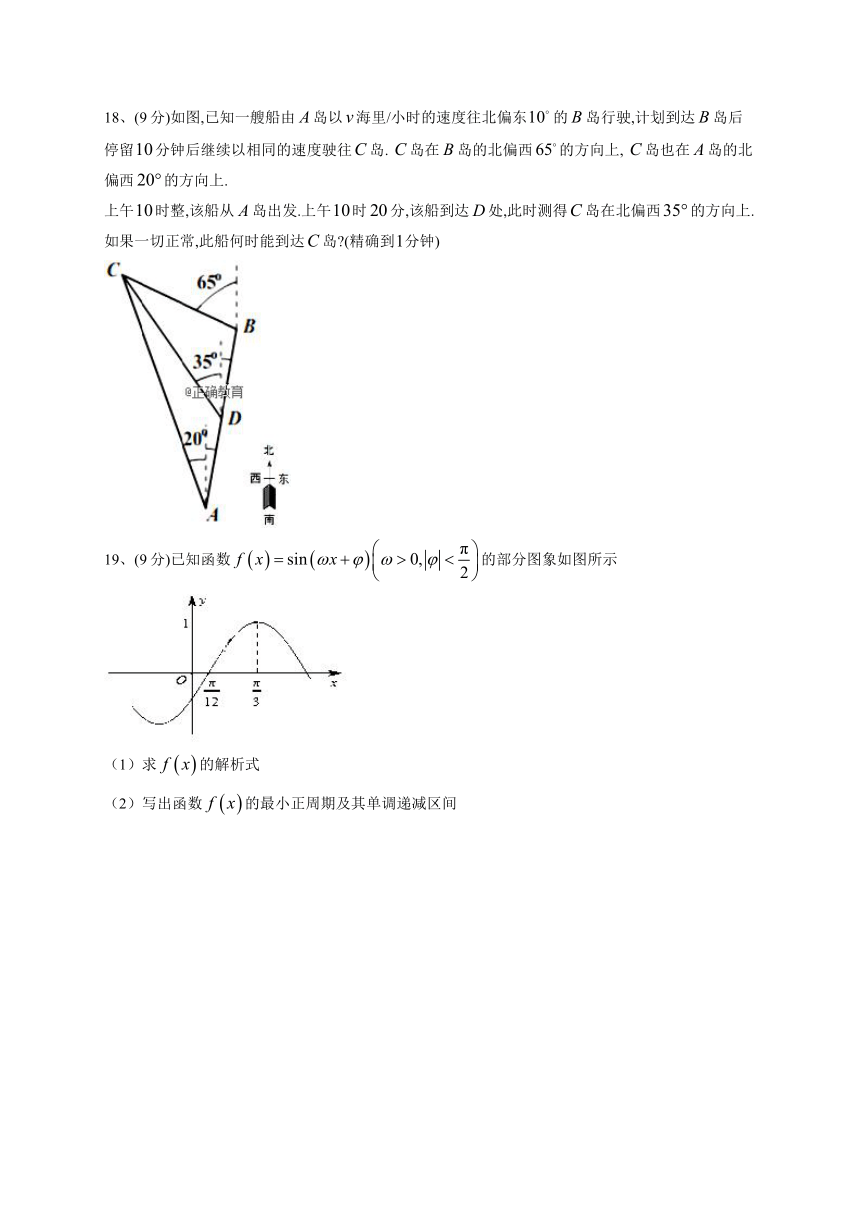
18、(9分)如图,已知一艘船由岛以海里/小时的速度往北偏东的岛行驶,计划到达岛后停留分钟后继续以相同的速度驶往岛. 岛在岛的北偏西的方向上, 岛也在岛的北偏西的方向上.
上午时整,该船从岛出发.上午时分,该船到达处,此时测得岛在北偏西的方向上.
如果一切正常,此船何时能到达岛 (精确到分钟)
19、(9分)已知函数的部分图象如图所示
(1)求的解析式
(2)写出函数的最小正周期及其单调递减区间
参考答案
1、答案:A
解析:由题图知,函数的周期,所以,则,将点代入,可得,,.又,,故函数解析式为,将代入函数解析式,得.
2、答案:C
解析:由,,得,,所以函数的增区间为,.当时,,而,故选C.
3、答案:D
解析:3月份达到最高价9千元,7月份价格最低为5千元,所以当时,函数有最大值为9;当时,函数有最小值为5.
所以所以,,
因为函数的周期,
所以由,得,
因为当时,函数有最大值,所以,
即,因为,取,得,
所以的解析式为: .
故选D项.
4、答案:D
解析:∵
5、答案:C
解析:
6、答案:B
解析:对于函数,令,
求得,,故它的图象的对称轴为,,故A不正确.
令,求得,,故它的图象的对称中心为,,故B正确.
令,求得,,
故它增区间,,故C不正确.
该函数的最小正周期为,故D错误,
故选:B.
由题意利用正弦函数的图象和性质,逐一判断各个选项是否正确,从而得出结论.
本题主要考查正弦函数的图象和性质,属于基础题.
7、答案:D
解析:由已知可得,该函数的周期.当时,.可得函数的单调递增区间是和.
8、答案:C
解析:由题图易得,则,.
9、答案:C
解析:由于,故函数的周期,所以,即每分钟心跳的次数为80.故选C.
10、答案:B
解析:由题中表格知,
所以,,.
故选B.
11、答案:20.5
解析:当时,;当时,.解得.所以当时,.
12、答案:0.8
解析:由图像知,周期,则这个简谐运动需要0.8s往返一次.
13、答案:
解析:如图所示,经过t秒钟,秒针转过的角度为.取AB的中点C,连接OC,则.
14、答案:
解析:由,得,所以,
由,得,
∴当时,,
;
故答案为.
15、答案:① ③
解析:∵,
∴ ① 正确,② ④不正确;而③ 中,故是对称中心.
16、答案:(1)由表中数据知,周期.
由,得.
由,得..
.
(2)..
..
又.
冲浪爱好者从9时到15时,有6小时可进行运动.
解析:
17、答案:(1)由函数关系式易知,当时,函数取得最大值,此时温度最高,为30℃,当时,函数取得最小值,此时温度最低,为10℃,所以最大温差为.
(2)令,得,
因为,所以.
令,得,
因为,所以.
故在这段时间内该细菌能存活的最长时间为(小时).
解析:
18、答案:在中, ,,
根据正弦定理得, ,即.
在中, ,,
根据正弦定理得, ,
即.
所以,
即,
从而,此船行驶和共需分钟.
故由岛出发至到达岛全程需要分钟.
即该船于时分到达岛
解析:
19、答案:(1)
将代入得,
∵
(2)
∴函数的最小正周期为π
∵为的单调递减区间
的单调递减区间为
解析:
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)电流强度I(安培)随时间t(秒)变化的函数的图象如图所示,则时的电流强度为( )
A.0安培 B.安培 C.安培 D.安培
2、(4分)商场人流量被定义为每分钟通过入口的人数,五一某商场的人流量满足函数,则下列时间段内人流量是增加的是( )
A. B. C. D.
3、(4分)某种商品一年内每件出厂价在7千元的基础上,按月呈的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定的解析式为( )
A.
B.
C.
D.
4、(4分)如图,单摆从某点开始来回摆动,离开平衡位置的距离和时间的函数关系式为,那么单摆来回摆动一次所需的时间为( )
A.
B.
C.
D.
5、(4分)已知函数的图象如图所示,则下列说法正确的是( )
A.函数的周期为π
B.函数为偶函数
C.函数在上单调递增
D.函数的图象关于点对称
6、(4分)已知函数,则以下说法正确的是( )
A. 的对称轴为
B. 的对称中心为
C. 的单调增区间为
D. 的周期为
7、(4分)动点在圆上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知当时间时,点A的坐标是,则当时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A. B. C. D.和
8、(4分)如图,某港口一天6时到18时的水深变化曲线近似满足函数,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
9、(4分)某人的血压满足函数关系式,其中为血压,t为时间,则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
10、(4分)已知某帆船中心比赛场馆区的海面上海浪高度:y(米)可看作时间t(,单位:时)的函数,记作,经长期观测, 的曲线可近似地看成是函数的图象,下表是某日各时的浪高数据:
0 3 6 9 12 15 18 21 24
2 1.5 1 1.5 2 1.5 0.99 1.5 2
则最能近似地表示表中数据间对应关系的函数是( )
A. B.
C. D.
二、填空题(共25分)
11、(5分)某城市一年中12个月的平均气温y与月份x的关系可近似地用函数来表示.已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为_____________℃.
12、(5分)如图为某简谐运动的图像,这个简谐运动需要_______s往返一次.
13、(5分)某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间时,点A与钟面上标12的点B重合,将A,B两点的距离d(cm)表示成t(s)的函数,则________,.
14、(5分)已知的周期为π,则当时的最小值为________
15、(5分)关于函数有下列命题,其中正确的是__________
① 的表达式可改写为;
② 是以为最小正周期的周期函数;
③ 的图象关于点对称;
④ 的图象关于直线对称.
三、解答题(共35分)
16、(8分)已知某海滨浴场的海浪高度y(米)是时间t(,单位:时)的函数,记作,下表是某日某时的浪高数据.
t/时 0 3 6 9 12 15 18 21 24
y/米 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,的曲线可近似地看成是函数.
(1)根据上表数据,求函数的最小正周期T、振幅A及函数解析式.
(2)依据规定,当海浪高度等于或高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内8时至20时之间,有多长时间可供冲浪爱好者进行运动?
17、(9分)已知某地一天从4~16时的温度变化曲线近似满足函数.
(1)求该地区这一段时间内温度的最大温差.
(2)若有一种细菌在15℃到25℃之间可以生存,则在这段时间内,该细菌最多能生存多长时间?
18、(9分)如图,已知一艘船由岛以海里/小时的速度往北偏东的岛行驶,计划到达岛后停留分钟后继续以相同的速度驶往岛. 岛在岛的北偏西的方向上, 岛也在岛的北偏西的方向上.
上午时整,该船从岛出发.上午时分,该船到达处,此时测得岛在北偏西的方向上.
如果一切正常,此船何时能到达岛 (精确到分钟)
19、(9分)已知函数的部分图象如图所示
(1)求的解析式
(2)写出函数的最小正周期及其单调递减区间
参考答案
1、答案:A
解析:由题图知,函数的周期,所以,则,将点代入,可得,,.又,,故函数解析式为,将代入函数解析式,得.
2、答案:C
解析:由,,得,,所以函数的增区间为,.当时,,而,故选C.
3、答案:D
解析:3月份达到最高价9千元,7月份价格最低为5千元,所以当时,函数有最大值为9;当时,函数有最小值为5.
所以所以,,
因为函数的周期,
所以由,得,
因为当时,函数有最大值,所以,
即,因为,取,得,
所以的解析式为: .
故选D项.
4、答案:D
解析:∵
5、答案:C
解析:
6、答案:B
解析:对于函数,令,
求得,,故它的图象的对称轴为,,故A不正确.
令,求得,,故它的图象的对称中心为,,故B正确.
令,求得,,
故它增区间,,故C不正确.
该函数的最小正周期为,故D错误,
故选:B.
由题意利用正弦函数的图象和性质,逐一判断各个选项是否正确,从而得出结论.
本题主要考查正弦函数的图象和性质,属于基础题.
7、答案:D
解析:由已知可得,该函数的周期.当时,.可得函数的单调递增区间是和.
8、答案:C
解析:由题图易得,则,.
9、答案:C
解析:由于,故函数的周期,所以,即每分钟心跳的次数为80.故选C.
10、答案:B
解析:由题中表格知,
所以,,.
故选B.
11、答案:20.5
解析:当时,;当时,.解得.所以当时,.
12、答案:0.8
解析:由图像知,周期,则这个简谐运动需要0.8s往返一次.
13、答案:
解析:如图所示,经过t秒钟,秒针转过的角度为.取AB的中点C,连接OC,则.
14、答案:
解析:由,得,所以,
由,得,
∴当时,,
;
故答案为.
15、答案:① ③
解析:∵,
∴ ① 正确,② ④不正确;而③ 中,故是对称中心.
16、答案:(1)由表中数据知,周期.
由,得.
由,得..
.
(2)..
..
又.
冲浪爱好者从9时到15时,有6小时可进行运动.
解析:
17、答案:(1)由函数关系式易知,当时,函数取得最大值,此时温度最高,为30℃,当时,函数取得最小值,此时温度最低,为10℃,所以最大温差为.
(2)令,得,
因为,所以.
令,得,
因为,所以.
故在这段时间内该细菌能存活的最长时间为(小时).
解析:
18、答案:在中, ,,
根据正弦定理得, ,即.
在中, ,,
根据正弦定理得, ,
即.
所以,
即,
从而,此船行驶和共需分钟.
故由岛出发至到达岛全程需要分钟.
即该船于时分到达岛
解析:
19、答案:(1)
将代入得,
∵
(2)
∴函数的最小正周期为π
∵为的单调递减区间
的单调递减区间为
解析:
