2022-2023学年人教B版2019必修四9.2 正弦定理与余弦定理的应用 同步课时训练(Word版含解析)
文档属性
| 名称 | 2022-2023学年人教B版2019必修四9.2 正弦定理与余弦定理的应用 同步课时训练(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 426.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 11:45:22 | ||
图片预览




文档简介
9.2 正弦定理与余弦定理的应用 同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)如图,位于A处的海面观测站获悉,在其正东方向相距40海里的B处有一艘渔船遇险,并在原地等待营救,在A处南偏西30°且相距20海里的C处有一艘救援船,则该船到救助处B的距离为( ).
A.2800海里 B.1200海里 C.海里 D.海里
2、(4分)如图,A,B两点在河的两岸,为测量A,B两点间的距离,测量人员在A的同侧选定一点C,测出A,C两点间的距离为60米,,,则A,B两点间的距离为( )
A.米 B.米 C.米 D.米
3、(4分)一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱的水柱的高度,某人在喷水柱正西方向的D处测得水柱顶端A的仰角为45°,沿D向北偏东30°方向前进100m后到达C处,在C处测得水柱顶端A的仰角为30°,则水柱的高度是( )
A.50m B.100m C.120m D.150m
4、(4分)为了测量B,C之间的距离,在河岸A,C处测量,如图:测得下面四组数据,较合理的是( )
A.与 B.与
C.与 D.与
5、(4分)某船只在海面上向正东方向行驶了x km迅速将航向调整为南偏西60°,然后沿着新的方向行驶了,此时发现离出发点恰好3 km,那么x的值为( )
A.3 B.6 C.3或6 D.4或6
6、(4分)小强站在地面上观察一个建在山顶上的建筑物,测得其视角为,同时测得观察该建筑物顶部的仰角为,则小强观测山顶的仰角为( )
A. B. C. D.
7、(4分)如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的倾斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的倾斜度为45°,若,山坡对于地平面的坡度为,则等于( )
A. B. C. D.
8、(4分)某同学骑电动自行车以24km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15min后到,点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是( )
A. B. C. D.
9、(4分)已知A,B两地的距离为10 km,B,C两地的距离为20 km,现测得,则A,C两地的距离为( )
A. B.10 km C. D.
10、(4分)如图,为了测量某湿地A,B两点间的距离,观察者找到在同一条直线上的三点C,D,E.从D点测得,从C点测得,,从E点测得.若测得,(单位:百米),则A,B两点间的距离为( )
A. B. C.3 D.
二、填空题(共25分)
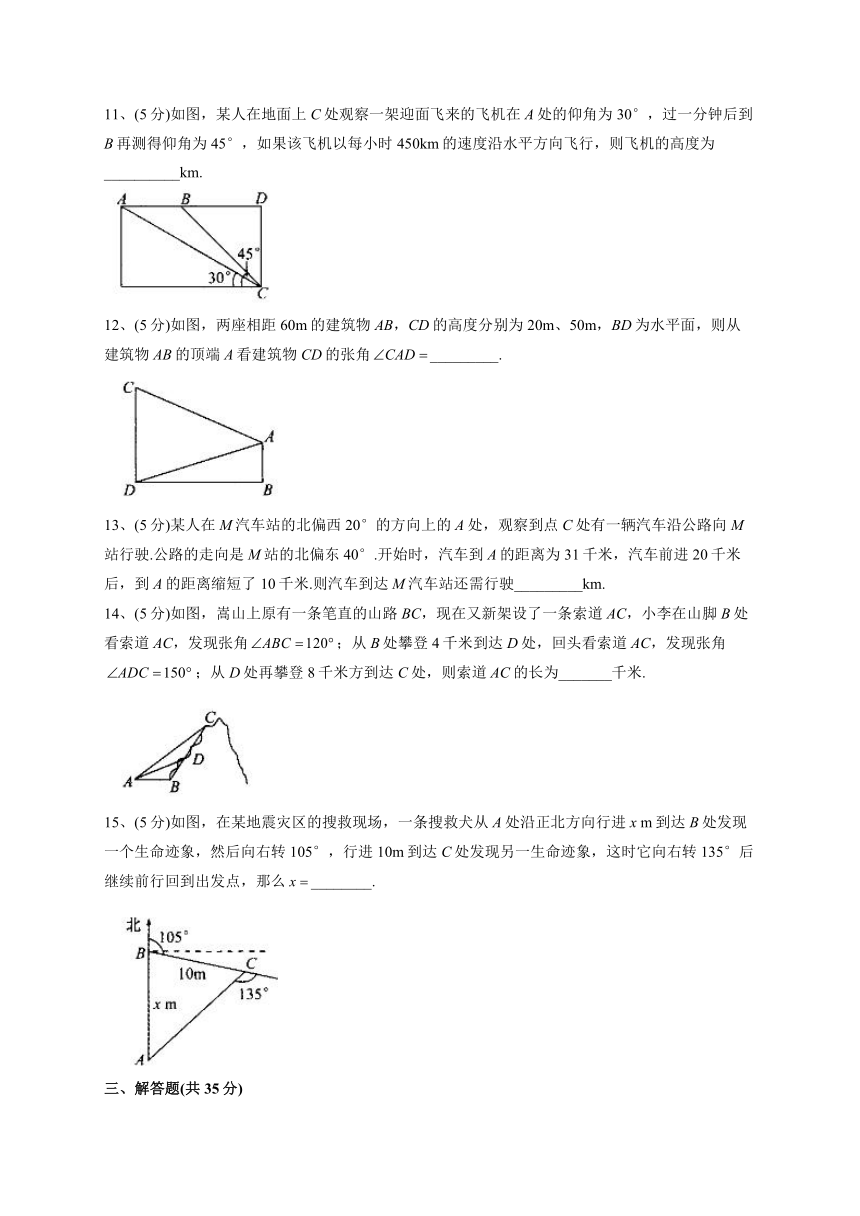
11、(5分)如图,某人在地面上C处观察一架迎面飞来的飞机在A处的仰角为30°,过一分钟后到B再测得仰角为45°,如果该飞机以每小时450km的速度沿水平方向飞行,则飞机的高度为__________km.
12、(5分)如图,两座相距60m的建筑物AB,CD的高度分别为20m、50m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角_________.
13、(5分)某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶.公路的走向是M站的北偏东40°.开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.则汽车到达M汽车站还需行驶_________km.
14、(5分)如图,嵩山上原有一条笔直的山路BC,现在又新架设了一条索道AC,小李在山脚B处看索道AC,发现张角;从B处攀登4千米到达D处,回头看索道AC,发现张角;从D处再攀登8千米方到达C处,则索道AC的长为_______千米.
15、(5分)如图,在某地震灾区的搜救现场,一条搜救犬从A处沿正北方向行进x m到达B处发现一个生命迹象,然后向右转105°,行进10m到达C处发现另一生命迹象,这时它向右转135°后继续前行回到出发点,那么________.
三、解答题(共35分)
16、(8分)如图,一架飞机从A地飞往B地,两地相距200km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成角的方向飞行,飞行到C地,再沿与原来的飞行方向成角的方向继续飞行km到达终点.
(1)求A,C两地之间的距离;
(2)求.
17、(9分)“如图,此人由南向北行驶,在C处测得塔AB在北偏东15°()方向上,匀速向北骑行20分钟到达E处,测得塔AB位于北偏东60°()方向上,此时测得塔顶A的仰角为60°,若塔AB高为千米”.
(1)此人骑行的速度是每小时多少千米?
(2)若此人继续骑行10分钟到达D处,问此时塔AB位于D处的南偏东什么方向?
18、(9分)某登山队在山脚A处测得山顶B的仰角为35°,沿倾斜角为20°的斜坡前进1000m后到达D处,又测得山顶的仰角为65°,求此山的高度.(精确到,参考数据:)
19、(9分)某校要在一条水泥路边安装路灯,其中灯杆的设计如图所示,AB为地面,CD,CE为路灯灯杆,,,在E处安装路灯,且路灯的照明张角,已知m,m.
(1)当M,D重合时,求路灯在路面的照明宽度MN;
(2)求此路灯在路面上的照明宽度MN的最小值.
参考答案
1、答案:D
解析:由已知得海里,海里,,在中,由余弦定理得(海里).故选D.
2、答案:A
解析:由正弦定理可知,
3、答案:A
解析:
4、答案:D
解析:
5、答案:C
解析:
6、答案:C
解析:
7、答案:C
解析:
8、答案:B
解析:
9、答案:D
解析:在中,,,,由余弦定理得,所以.故选D.
10、答案:C
解析:在中,,,则,.在中,,,则,由正弦定理,得.则在中,,,,由余弦定理得,则.故选C.
11、答案:
解析:如题图,,设飞机高为h km,
则.
又,
由得.
所以.
12、答案:45°
解析:依题意可得,
又,所以在中,由余弦定理的推论得,
又,所以,
所以从建筑物AB的顶端A看建筑物CD的张角为45°.
13、答案:15
解析:由题意,画出北示意图,设汽车前进20千米后到达B处.
在中,,
由余弦定理,得,
则,
所以.
在中,由正弦定理,得.
从而有.
故汽车到达M汽车站还需行驶15km.
14、答案:
解析:因为,所以,
在中,千米,千米,
在中,千米,,所以,
所以千米.
15、答案:
解析:由题意,所以,
因为,所以.
16、答案:(1)km
(2)
解析:(1)由余弦定理可得
,
所以,km.
(2)(方法一)由正弦定理得,
则,
因为,
所以A为锐角,所以,
故.
(方法二)由余弦定理可得,
所以,,
则为锐角,故,
因此,.
17、答案:(1)每小时千米.
(2)南偏东45°.
解析:(1)在中,,
所以千米,因为,所以.
在中,由正弦定理得千米,
千米/时,
所以此人骑行的速度是每小时千米.
(2) 千米.
在中,由余弦定理得,
所以千米,
在中,由正弦定理得,
所以,所以塔AB位于D处的南偏东45°.
18、答案:高度约为811m.
解析:如图,过点D作交BC于E,
因为,所以,
于是.
又,所以.
在中,由正弦定理,得.
在中,.
答:此山的高度约为811m.
19、答案:(1)路灯在路面的照明宽度为m
(2)照明宽度MN的最小值为m.
解析:解:(1)当M,D重合时,
由余弦定理知,,
所以,
因为,所以,
因为,所以,
因为,所以
,
在中,由正弦定理可知,,解得;
(2)易知E到地面的距离m,
由三角形面积公式可知,,
所以,
又由余弦定理可知,,
当且仅当时,等号成立,所以,解得.
照明宽度MN的最小值为m.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)如图,位于A处的海面观测站获悉,在其正东方向相距40海里的B处有一艘渔船遇险,并在原地等待营救,在A处南偏西30°且相距20海里的C处有一艘救援船,则该船到救助处B的距离为( ).
A.2800海里 B.1200海里 C.海里 D.海里
2、(4分)如图,A,B两点在河的两岸,为测量A,B两点间的距离,测量人员在A的同侧选定一点C,测出A,C两点间的距离为60米,,,则A,B两点间的距离为( )
A.米 B.米 C.米 D.米
3、(4分)一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱的水柱的高度,某人在喷水柱正西方向的D处测得水柱顶端A的仰角为45°,沿D向北偏东30°方向前进100m后到达C处,在C处测得水柱顶端A的仰角为30°,则水柱的高度是( )
A.50m B.100m C.120m D.150m
4、(4分)为了测量B,C之间的距离,在河岸A,C处测量,如图:测得下面四组数据,较合理的是( )
A.与 B.与
C.与 D.与
5、(4分)某船只在海面上向正东方向行驶了x km迅速将航向调整为南偏西60°,然后沿着新的方向行驶了,此时发现离出发点恰好3 km,那么x的值为( )
A.3 B.6 C.3或6 D.4或6
6、(4分)小强站在地面上观察一个建在山顶上的建筑物,测得其视角为,同时测得观察该建筑物顶部的仰角为,则小强观测山顶的仰角为( )
A. B. C. D.
7、(4分)如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的倾斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的倾斜度为45°,若,山坡对于地平面的坡度为,则等于( )
A. B. C. D.
8、(4分)某同学骑电动自行车以24km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15min后到,点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是( )
A. B. C. D.
9、(4分)已知A,B两地的距离为10 km,B,C两地的距离为20 km,现测得,则A,C两地的距离为( )
A. B.10 km C. D.
10、(4分)如图,为了测量某湿地A,B两点间的距离,观察者找到在同一条直线上的三点C,D,E.从D点测得,从C点测得,,从E点测得.若测得,(单位:百米),则A,B两点间的距离为( )
A. B. C.3 D.
二、填空题(共25分)
11、(5分)如图,某人在地面上C处观察一架迎面飞来的飞机在A处的仰角为30°,过一分钟后到B再测得仰角为45°,如果该飞机以每小时450km的速度沿水平方向飞行,则飞机的高度为__________km.
12、(5分)如图,两座相距60m的建筑物AB,CD的高度分别为20m、50m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角_________.
13、(5分)某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶.公路的走向是M站的北偏东40°.开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.则汽车到达M汽车站还需行驶_________km.
14、(5分)如图,嵩山上原有一条笔直的山路BC,现在又新架设了一条索道AC,小李在山脚B处看索道AC,发现张角;从B处攀登4千米到达D处,回头看索道AC,发现张角;从D处再攀登8千米方到达C处,则索道AC的长为_______千米.
15、(5分)如图,在某地震灾区的搜救现场,一条搜救犬从A处沿正北方向行进x m到达B处发现一个生命迹象,然后向右转105°,行进10m到达C处发现另一生命迹象,这时它向右转135°后继续前行回到出发点,那么________.
三、解答题(共35分)
16、(8分)如图,一架飞机从A地飞往B地,两地相距200km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成角的方向飞行,飞行到C地,再沿与原来的飞行方向成角的方向继续飞行km到达终点.
(1)求A,C两地之间的距离;
(2)求.
17、(9分)“如图,此人由南向北行驶,在C处测得塔AB在北偏东15°()方向上,匀速向北骑行20分钟到达E处,测得塔AB位于北偏东60°()方向上,此时测得塔顶A的仰角为60°,若塔AB高为千米”.
(1)此人骑行的速度是每小时多少千米?
(2)若此人继续骑行10分钟到达D处,问此时塔AB位于D处的南偏东什么方向?
18、(9分)某登山队在山脚A处测得山顶B的仰角为35°,沿倾斜角为20°的斜坡前进1000m后到达D处,又测得山顶的仰角为65°,求此山的高度.(精确到,参考数据:)
19、(9分)某校要在一条水泥路边安装路灯,其中灯杆的设计如图所示,AB为地面,CD,CE为路灯灯杆,,,在E处安装路灯,且路灯的照明张角,已知m,m.
(1)当M,D重合时,求路灯在路面的照明宽度MN;
(2)求此路灯在路面上的照明宽度MN的最小值.
参考答案
1、答案:D
解析:由已知得海里,海里,,在中,由余弦定理得(海里).故选D.
2、答案:A
解析:由正弦定理可知,
3、答案:A
解析:
4、答案:D
解析:
5、答案:C
解析:
6、答案:C
解析:
7、答案:C
解析:
8、答案:B
解析:
9、答案:D
解析:在中,,,,由余弦定理得,所以.故选D.
10、答案:C
解析:在中,,,则,.在中,,,则,由正弦定理,得.则在中,,,,由余弦定理得,则.故选C.
11、答案:
解析:如题图,,设飞机高为h km,
则.
又,
由得.
所以.
12、答案:45°
解析:依题意可得,
又,所以在中,由余弦定理的推论得,
又,所以,
所以从建筑物AB的顶端A看建筑物CD的张角为45°.
13、答案:15
解析:由题意,画出北示意图,设汽车前进20千米后到达B处.
在中,,
由余弦定理,得,
则,
所以.
在中,由正弦定理,得.
从而有.
故汽车到达M汽车站还需行驶15km.
14、答案:
解析:因为,所以,
在中,千米,千米,
在中,千米,,所以,
所以千米.
15、答案:
解析:由题意,所以,
因为,所以.
16、答案:(1)km
(2)
解析:(1)由余弦定理可得
,
所以,km.
(2)(方法一)由正弦定理得,
则,
因为,
所以A为锐角,所以,
故.
(方法二)由余弦定理可得,
所以,,
则为锐角,故,
因此,.
17、答案:(1)每小时千米.
(2)南偏东45°.
解析:(1)在中,,
所以千米,因为,所以.
在中,由正弦定理得千米,
千米/时,
所以此人骑行的速度是每小时千米.
(2) 千米.
在中,由余弦定理得,
所以千米,
在中,由正弦定理得,
所以,所以塔AB位于D处的南偏东45°.
18、答案:高度约为811m.
解析:如图,过点D作交BC于E,
因为,所以,
于是.
又,所以.
在中,由正弦定理,得.
在中,.
答:此山的高度约为811m.
19、答案:(1)路灯在路面的照明宽度为m
(2)照明宽度MN的最小值为m.
解析:解:(1)当M,D重合时,
由余弦定理知,,
所以,
因为,所以,
因为,所以,
因为,所以
,
在中,由正弦定理可知,,解得;
(2)易知E到地面的距离m,
由三角形面积公式可知,,
所以,
又由余弦定理可知,,
当且仅当时,等号成立,所以,解得.
照明宽度MN的最小值为m.
