2022-2023学年人教B版2019必修四11.1空间几何体 同步课时训练(Word版含解析)
文档属性
| 名称 | 2022-2023学年人教B版2019必修四11.1空间几何体 同步课时训练(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 470.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 11:48:17 | ||
图片预览



文档简介
11.1 空间几何体 同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)下列说法正确的是( )
A.相等的角在直观图中仍然相等
B.相等的线段在直观图中仍然相等
C.正方形的直观图是正方形
D.若两条线段平行,则在直观图中对应的两条线段仍然平行
2、(4分)若圆台的上、下底面面积分别为4,16,则圆台的中截面的面积为( ).
A.10 B.8 C.9 D.
3、(4分)利用斜二测画法可以得到:
①三角形的直观图是三角形;
②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形;
④菱形的直观图是菱形.
以上结论正确的有( )
A. ①② B.① C. ③④ D. ①②③④
4、(4分)已知圆锥的表面积为,它的侧面展开图是一个半圆,则此圆锥的体积为( )
A. B. C. D.
5、(4分)如图,三棱锥的四个面都为直角三角形,平面ABC,,,三棱锥的四个顶点都在球O的球面上,现在球O内任取一点,则该点取自三棱锥内的概率为( )
A. B. C. D.
6、(4分)在轴截面顶角为直角的圆锥内,作一内接圆柱,若圆柱的表面积等于圆锥的侧面积,则圆锥的底面半径与圆柱的底面半径之比为( )
A. B.2 C. D.4
7、(4分)已知正三棱柱的所有顶点都在球O的球面上,且该正三棱柱的底面边长为2,体积为3,则球O的表面积为( )
A. B. C. D.
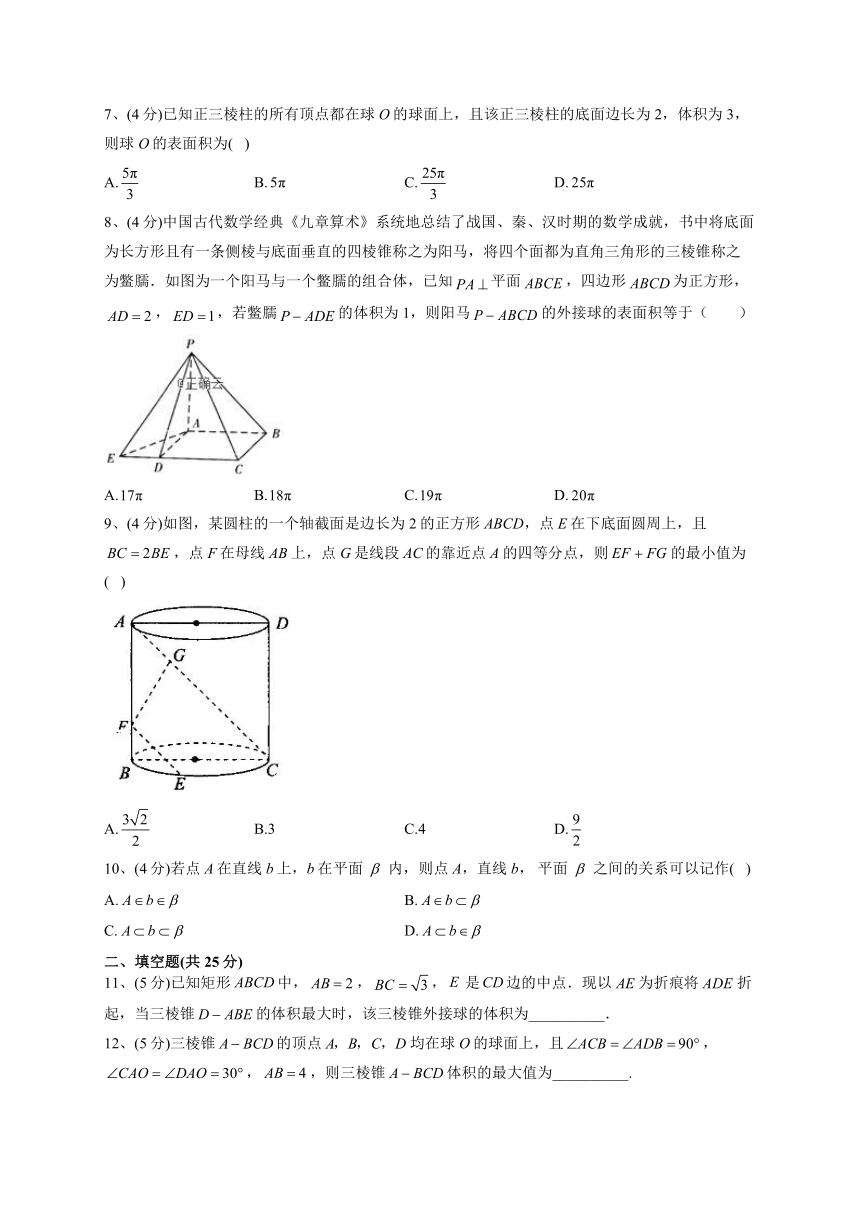
8、(4分)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑.如图为一个阳马与一个鳖臑的组合体,已知平面,四边形为正方形,,,若鳖臑的体积为1,则阳马的外接球的表面积等于( )
A. B. C. D.
9、(4分)如图,某圆柱的一个轴截面是边长为2的正方形ABCD,点E在下底面圆周上,且,点F在母线AB上,点G是线段AC的靠近点A的四等分点,则的最小值为( )
A. B.3 C.4 D.
10、(4分)若点A在直线b上,b在平面内,则点A,直线b, 平面之间的关系可以记作( )
A. B.
C. D.
二、填空题(共25分)
11、(5分)已知矩形中,,,是边的中点.现以为折痕将折起,当三棱锥的体积最大时,该三棱锥外接球的体积为__________.
12、(5分)三棱锥的顶点均在球O的球面上,且,,,则三棱锥体积的最大值为__________.
13、(5分)已知与是两个不重合的平面,则下列推理正确个数是__________.
①;
②;
③;
④.
14、(5分)过球一条半径的中点,作一垂直于这个半径的截面,截面面积为,则球的表面积为_________________.
15、(5分)四棱锥中,底面ABCD是边长为2的正方形,侧面SAD是以SD为斜边的等腰直角三角形,若,则四棱锥的体积取值范围为_____.
三、解答题(共35分)
16、(8分)如图所示,长方体.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为 什么?
(2)用平面BCNM把这个长方体分成两部分,各部分 形成的几何体还是棱柱吗?如果是,是几棱柱,并用符 号表示;如果不是,请说明理由.
17、(9分)如图,已知正三棱锥的侧面是直角三角形,,顶点P在平面内的正投影为点在平面内的正投影为点E,连接并延长交交于点G.
(1)证明:G是的中点;
(2)在图中作出点E在平面内的正投影F(说明作法及理由),并求四面体的体积.
18、(9分)现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥,下部分的形状是正四棱柱(如图所示),并要求正四棱柱的高是正四棱锥的高的4倍.若,,求仓库的容积.
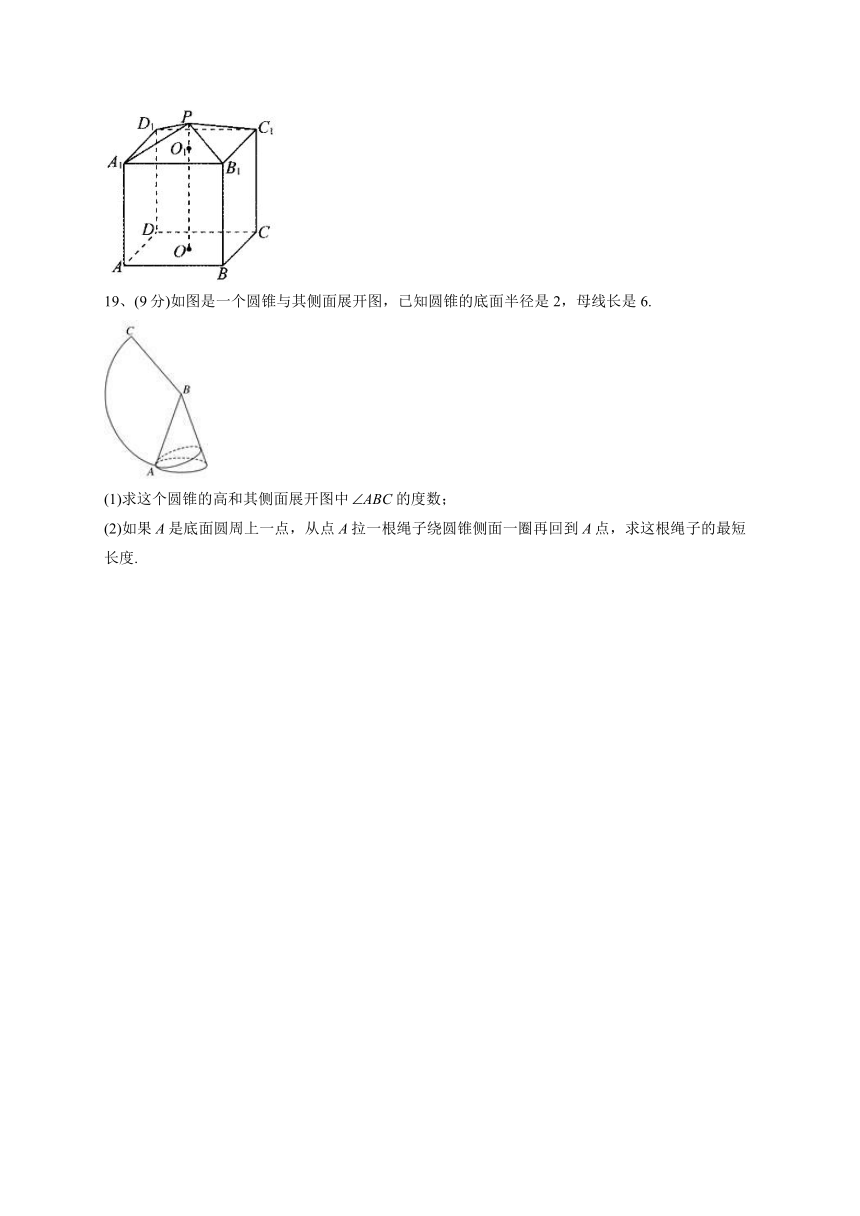
19、(9分)如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
(1)求这个圆锥的高和其侧面展开图中的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
参考答案
1、答案:D
解析:等腰三角形的两底角相等,但在直观图不相等,故A错误.
正方形的两邻边相等, 但在直观图中不相等,故B,C错误. 故选D
2、答案:C
解析:设圆台的上、下底面半径分别为、,圆台中截面的半径为,则,,解得,,所以,所以.
3、答案:A
解析:根据斜二测画法可知,只有平行于x轴的线段长度和方向都不变,平行于y轴的线段倾斜或者,并且长度减半,所以①三角形的直观图和原三角形相比只是面积变小了,它还是三角形;②平行四边形的直观图还是平行四边形;③正方形的直观图是平行四边形;④菱形的直观图是平行四边形.所以①②正确.故选A.
4、答案:A
解析:设圆锥的底面半径为 ,高为 ,母线为,
因为其表面积为 ,
所以 ,
即
又因为它的侧面展开图是一个半圆,
所以 ,
即
所以 ,
所以此圆锥的体积为.
故选: A
5、答案:D
解析:根据题意,可以将三棱锥补全为长方体,其中长方体的底面是边长为1的正方形,高为.设三棱锥外接球的半径为R,所以三棱锥外接球的直径为长方体的体对角线,即,所以.由于三棱锥的体积,三棱锥外接球的体积,所以在球O内任取一点,该点取自三棱锥内的概率.
6、答案:A
解析:
7、答案:C
解析:
8、答案:A
解析:∵平面,∴,解得,
而阳马的外接球的直径是以AD,AB,AP为宽,长,高的长方体的体对角线,
∴,即,
球的表面积为.
故选:A.
9、答案:A
解析:如图,将绕AB旋转到的位置,并且点P在CB的延长线上,连接PG,交AB于点F,此时最小.
由已知可知轴截面ABCD是边长为2的正方形,所以.
在中,由余弦定理得,.故选A.
10、答案:B
解析:
11、答案:
解析:在矩形ABCD中,,,E是CD边中点,,中,,,是正三角形.面积为定值.只有平面平面ABCE时三棱锥的高最大.此时体积最大.取AE的中点F.连接FB.在正中,面ABE和面ADE交于AE.平面ADE,即是.正的中心为O在中O点到三棱锥四个顶点的距离是,O是外接球球心,是半径,三棱锥外接球体积.
12、答案:2
解析:
13、答案:3
解析:由基本事实2知,①正确;
由基本事实3知,②正确;
若,显然有,但是,③错误;④正确.
14、答案:
解析:易知截面为一圆面,如图所示,圆O是球的过已知半径的大圆,AB是截面圆的直径,作OC垂直AB于点C,连接OA.
由截面面积为,可得.
设,则,所以,解得.
故球的表面积.
15、答案:
解析:如图所示,四棱锥中,可得:;平面平面平面ABCD,过S作于O,则平面ABCD,故,在中,,设,则有,,又,则,四棱锥的体积取值范围为.
16、答案:(1)是棱柱,并且是四棱柱.
(2)见解析.
解析:(1)是棱柱,并且是四棱柱,因为以长方体相对的两个面作底面,是互相平行的,其余各面都是矩形,且四条侧棱互相平行,符合棱柱的定义.
(2)截面BCNM右上方部分是三棱柱,左下方部分是四棱柱.
17、答案:(1)见解析(2)
解析:(1)因为P在平面内的正投影为D,所以.
因为D在平面内的正投影为E,所以.
所以平面,故.
又由已知,可得,所以G是的中点.
(2)在平面内,过点E作的平行线交于点即为E在平面内的正投影.
理由如下:由已知可得,又,所以,,
因此平面,即点F为E在平面内的正投影.
连接,因此P在平面内的正投影为D,所以D是正三角形的中心.
由(1)知,G是的中点,所以D在上,故.
由题设可得平面平面,所以,因此.
由已知,正三棱锥的侧面是直角三角形且,可得.
在等腰直角三角形中,可得.
所以四面体的体积.
18、答案:仓库的容积为312
解析:由,得,则
,
,,
故仓库的容积为312().
19、答案:(1)
(2)这根绳子的最短长度是.
解析:(1)圆锥的高为,
底面圆的周长等于,
解得.
(2)连接AC,过B作于D,
则.
由,可求得,
,
,
即这根绳子的最短长度是.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)下列说法正确的是( )
A.相等的角在直观图中仍然相等
B.相等的线段在直观图中仍然相等
C.正方形的直观图是正方形
D.若两条线段平行,则在直观图中对应的两条线段仍然平行
2、(4分)若圆台的上、下底面面积分别为4,16,则圆台的中截面的面积为( ).
A.10 B.8 C.9 D.
3、(4分)利用斜二测画法可以得到:
①三角形的直观图是三角形;
②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形;
④菱形的直观图是菱形.
以上结论正确的有( )
A. ①② B.① C. ③④ D. ①②③④
4、(4分)已知圆锥的表面积为,它的侧面展开图是一个半圆,则此圆锥的体积为( )
A. B. C. D.
5、(4分)如图,三棱锥的四个面都为直角三角形,平面ABC,,,三棱锥的四个顶点都在球O的球面上,现在球O内任取一点,则该点取自三棱锥内的概率为( )
A. B. C. D.
6、(4分)在轴截面顶角为直角的圆锥内,作一内接圆柱,若圆柱的表面积等于圆锥的侧面积,则圆锥的底面半径与圆柱的底面半径之比为( )
A. B.2 C. D.4
7、(4分)已知正三棱柱的所有顶点都在球O的球面上,且该正三棱柱的底面边长为2,体积为3,则球O的表面积为( )
A. B. C. D.
8、(4分)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑.如图为一个阳马与一个鳖臑的组合体,已知平面,四边形为正方形,,,若鳖臑的体积为1,则阳马的外接球的表面积等于( )
A. B. C. D.
9、(4分)如图,某圆柱的一个轴截面是边长为2的正方形ABCD,点E在下底面圆周上,且,点F在母线AB上,点G是线段AC的靠近点A的四等分点,则的最小值为( )
A. B.3 C.4 D.
10、(4分)若点A在直线b上,b在平面内,则点A,直线b, 平面之间的关系可以记作( )
A. B.
C. D.
二、填空题(共25分)
11、(5分)已知矩形中,,,是边的中点.现以为折痕将折起,当三棱锥的体积最大时,该三棱锥外接球的体积为__________.
12、(5分)三棱锥的顶点均在球O的球面上,且,,,则三棱锥体积的最大值为__________.
13、(5分)已知与是两个不重合的平面,则下列推理正确个数是__________.
①;
②;
③;
④.
14、(5分)过球一条半径的中点,作一垂直于这个半径的截面,截面面积为,则球的表面积为_________________.
15、(5分)四棱锥中,底面ABCD是边长为2的正方形,侧面SAD是以SD为斜边的等腰直角三角形,若,则四棱锥的体积取值范围为_____.
三、解答题(共35分)
16、(8分)如图所示,长方体.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为 什么?
(2)用平面BCNM把这个长方体分成两部分,各部分 形成的几何体还是棱柱吗?如果是,是几棱柱,并用符 号表示;如果不是,请说明理由.
17、(9分)如图,已知正三棱锥的侧面是直角三角形,,顶点P在平面内的正投影为点在平面内的正投影为点E,连接并延长交交于点G.
(1)证明:G是的中点;
(2)在图中作出点E在平面内的正投影F(说明作法及理由),并求四面体的体积.
18、(9分)现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥,下部分的形状是正四棱柱(如图所示),并要求正四棱柱的高是正四棱锥的高的4倍.若,,求仓库的容积.
19、(9分)如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
(1)求这个圆锥的高和其侧面展开图中的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
参考答案
1、答案:D
解析:等腰三角形的两底角相等,但在直观图不相等,故A错误.
正方形的两邻边相等, 但在直观图中不相等,故B,C错误. 故选D
2、答案:C
解析:设圆台的上、下底面半径分别为、,圆台中截面的半径为,则,,解得,,所以,所以.
3、答案:A
解析:根据斜二测画法可知,只有平行于x轴的线段长度和方向都不变,平行于y轴的线段倾斜或者,并且长度减半,所以①三角形的直观图和原三角形相比只是面积变小了,它还是三角形;②平行四边形的直观图还是平行四边形;③正方形的直观图是平行四边形;④菱形的直观图是平行四边形.所以①②正确.故选A.
4、答案:A
解析:设圆锥的底面半径为 ,高为 ,母线为,
因为其表面积为 ,
所以 ,
即
又因为它的侧面展开图是一个半圆,
所以 ,
即
所以 ,
所以此圆锥的体积为.
故选: A
5、答案:D
解析:根据题意,可以将三棱锥补全为长方体,其中长方体的底面是边长为1的正方形,高为.设三棱锥外接球的半径为R,所以三棱锥外接球的直径为长方体的体对角线,即,所以.由于三棱锥的体积,三棱锥外接球的体积,所以在球O内任取一点,该点取自三棱锥内的概率.
6、答案:A
解析:
7、答案:C
解析:
8、答案:A
解析:∵平面,∴,解得,
而阳马的外接球的直径是以AD,AB,AP为宽,长,高的长方体的体对角线,
∴,即,
球的表面积为.
故选:A.
9、答案:A
解析:如图,将绕AB旋转到的位置,并且点P在CB的延长线上,连接PG,交AB于点F,此时最小.
由已知可知轴截面ABCD是边长为2的正方形,所以.
在中,由余弦定理得,.故选A.
10、答案:B
解析:
11、答案:
解析:在矩形ABCD中,,,E是CD边中点,,中,,,是正三角形.面积为定值.只有平面平面ABCE时三棱锥的高最大.此时体积最大.取AE的中点F.连接FB.在正中,面ABE和面ADE交于AE.平面ADE,即是.正的中心为O在中O点到三棱锥四个顶点的距离是,O是外接球球心,是半径,三棱锥外接球体积.
12、答案:2
解析:
13、答案:3
解析:由基本事实2知,①正确;
由基本事实3知,②正确;
若,显然有,但是,③错误;④正确.
14、答案:
解析:易知截面为一圆面,如图所示,圆O是球的过已知半径的大圆,AB是截面圆的直径,作OC垂直AB于点C,连接OA.
由截面面积为,可得.
设,则,所以,解得.
故球的表面积.
15、答案:
解析:如图所示,四棱锥中,可得:;平面平面平面ABCD,过S作于O,则平面ABCD,故,在中,,设,则有,,又,则,四棱锥的体积取值范围为.
16、答案:(1)是棱柱,并且是四棱柱.
(2)见解析.
解析:(1)是棱柱,并且是四棱柱,因为以长方体相对的两个面作底面,是互相平行的,其余各面都是矩形,且四条侧棱互相平行,符合棱柱的定义.
(2)截面BCNM右上方部分是三棱柱,左下方部分是四棱柱.
17、答案:(1)见解析(2)
解析:(1)因为P在平面内的正投影为D,所以.
因为D在平面内的正投影为E,所以.
所以平面,故.
又由已知,可得,所以G是的中点.
(2)在平面内,过点E作的平行线交于点即为E在平面内的正投影.
理由如下:由已知可得,又,所以,,
因此平面,即点F为E在平面内的正投影.
连接,因此P在平面内的正投影为D,所以D是正三角形的中心.
由(1)知,G是的中点,所以D在上,故.
由题设可得平面平面,所以,因此.
由已知,正三棱锥的侧面是直角三角形且,可得.
在等腰直角三角形中,可得.
所以四面体的体积.
18、答案:仓库的容积为312
解析:由,得,则
,
,,
故仓库的容积为312().
19、答案:(1)
(2)这根绳子的最短长度是.
解析:(1)圆锥的高为,
底面圆的周长等于,
解得.
(2)连接AC,过B作于D,
则.
由,可求得,
,
,
即这根绳子的最短长度是.
