2022-2023学年人教B版2019必修四11.3 空间中的平行关系 同步课时训练(Word版含解析)
文档属性
| 名称 | 2022-2023学年人教B版2019必修四11.3 空间中的平行关系 同步课时训练(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 524.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 11:49:57 | ||
图片预览


文档简介
11.3 空间中的平行关系 同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)如图,在棱长为1的正方体中,M,N分别是的中点,过直线BD的平面平面AMN,则平面截该正方体所得截面的面积为( )
A. B. C. D.
2、(4分)已知平面平面,直线,直线,下列结论中不正确的是( )
A. B.
C. D.m与n不相交
3、(4分)如图,在正方体中,M,N,P分别是的中点,则下列结论正确的是( )
A. B.
C.平面 D.平面BDP
4、(4分)已知平面平面,过平面内的一条直线a的平面,与平面相交,交线为直线b,则a,b的位置关系是( )
A.平行 B.相交 C.异面 D.不确定
5、(4分)下列命题中不正确的是( )
A.平面平面,一条直线a平行于平面,则a一定平行于平面
B.平面平面,则平面内的任意一条直线都平行于平面
C.一个三角形有两条边所在的直线分别平行于一个平面,那么该三角形所在的平面与这个平面平行
D.分别在两个平行平面内的两条直线只能是平行直线或异面直线
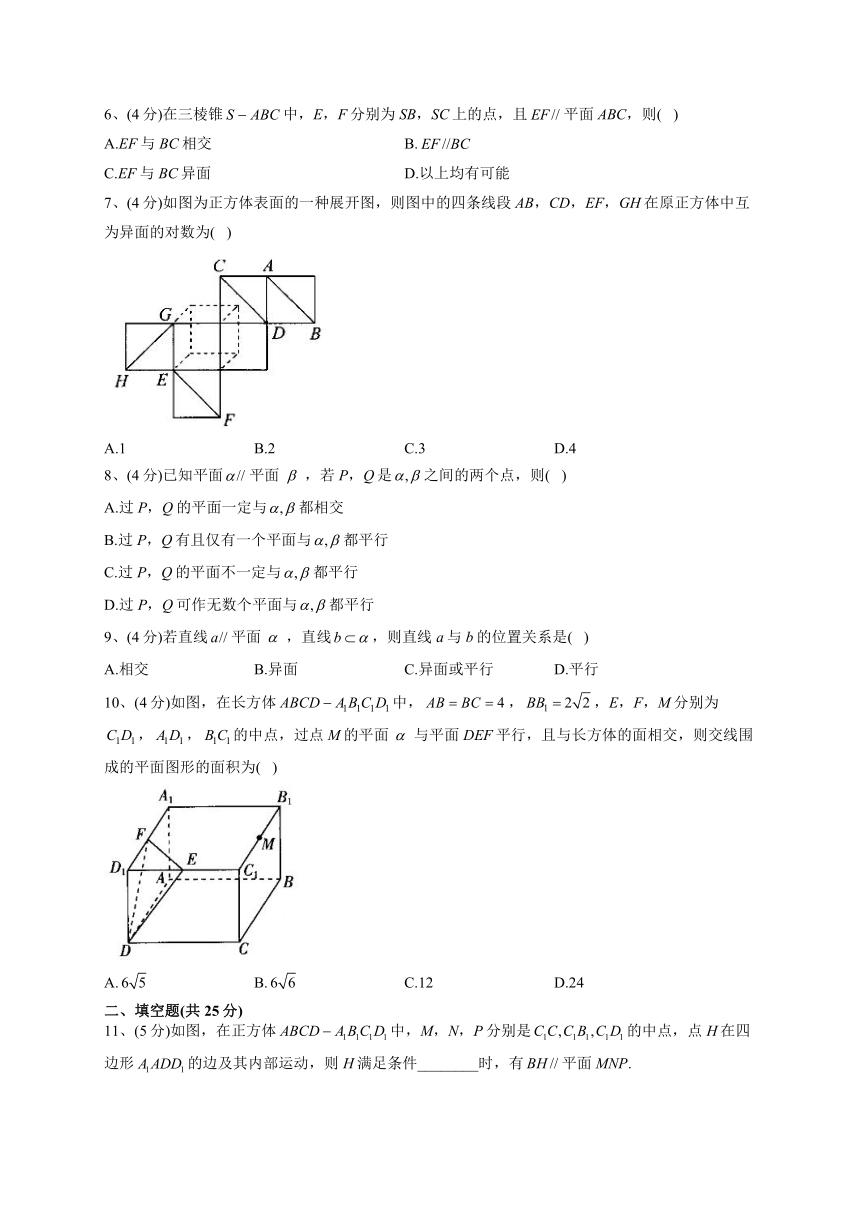
6、(4分)在三棱锥中,E,F分别为SB,SC上的点,且平面ABC,则( )
A.EF与BC相交 B.
C.EF与BC异面 D.以上均有可能
7、(4分)如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH在原正方体中互为异面的对数为( )
A.1 B.2 C.3 D.4
8、(4分)已知平面平面,若P,Q是之间的两个点,则( )
A.过P,Q的平面一定与都相交
B.过P,Q有且仅有一个平面与都平行
C.过P,Q的平面不一定与都平行
D.过P,Q可作无数个平面与都平行
9、(4分)若直线平面,直线,则直线a与b的位置关系是( )
A.相交 B.异面 C.异面或平行 D.平行
10、(4分)如图,在长方体中,,,E,F,M分别为,,的中点,过点M的平面与平面DEF平行,且与长方体的面相交,则交线围成的平面图形的面积为( )
A. B. C.12 D.24
二、填空题(共25分)
11、(5分)如图,在正方体中,M,N,P分别是的中点,点H在四边形的边及其内部运动,则H满足条件________时,有平面MNP.
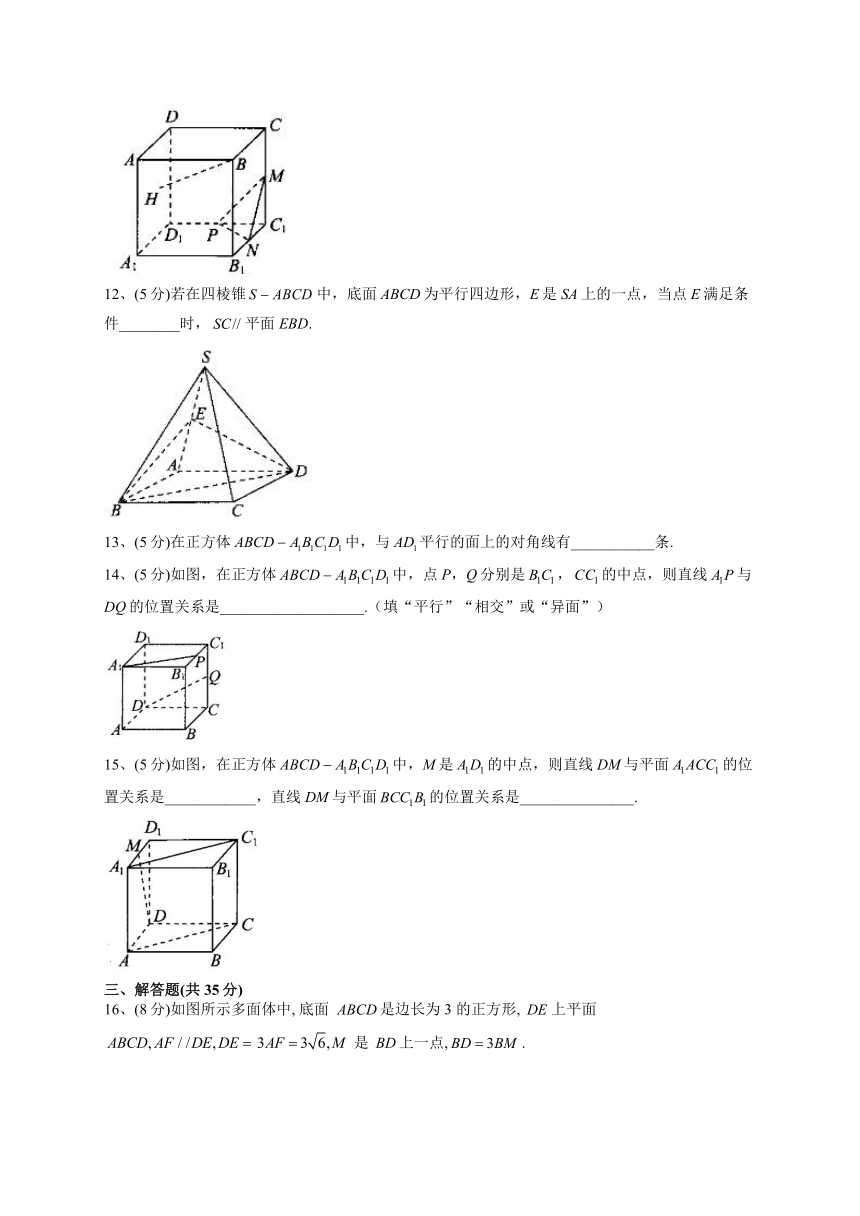
12、(5分)若在四棱锥中,底面ABCD为平行四边形,E是SA上的一点,当点E满足条件________时,平面EBD.
13、(5分)在正方体中,与平行的面上的对角线有___________条.
14、(5分)如图,在正方体中,点P,Q分别是,的中点,则直线与DQ的位置关系是___________________.(填“平行”“相交”或“异面”)
15、(5分)如图,在正方体中,M是的中点,则直线DM与平面的位置关系是____________,直线DM与平面的位置关系是_______________.
三、解答题(共35分)
16、(8分)如图所示多面体中, 底面 是边长为 3 的正方形, 上平面 是 上一点,.
(1)求证: 平面;
(2)求此多面体的体积.
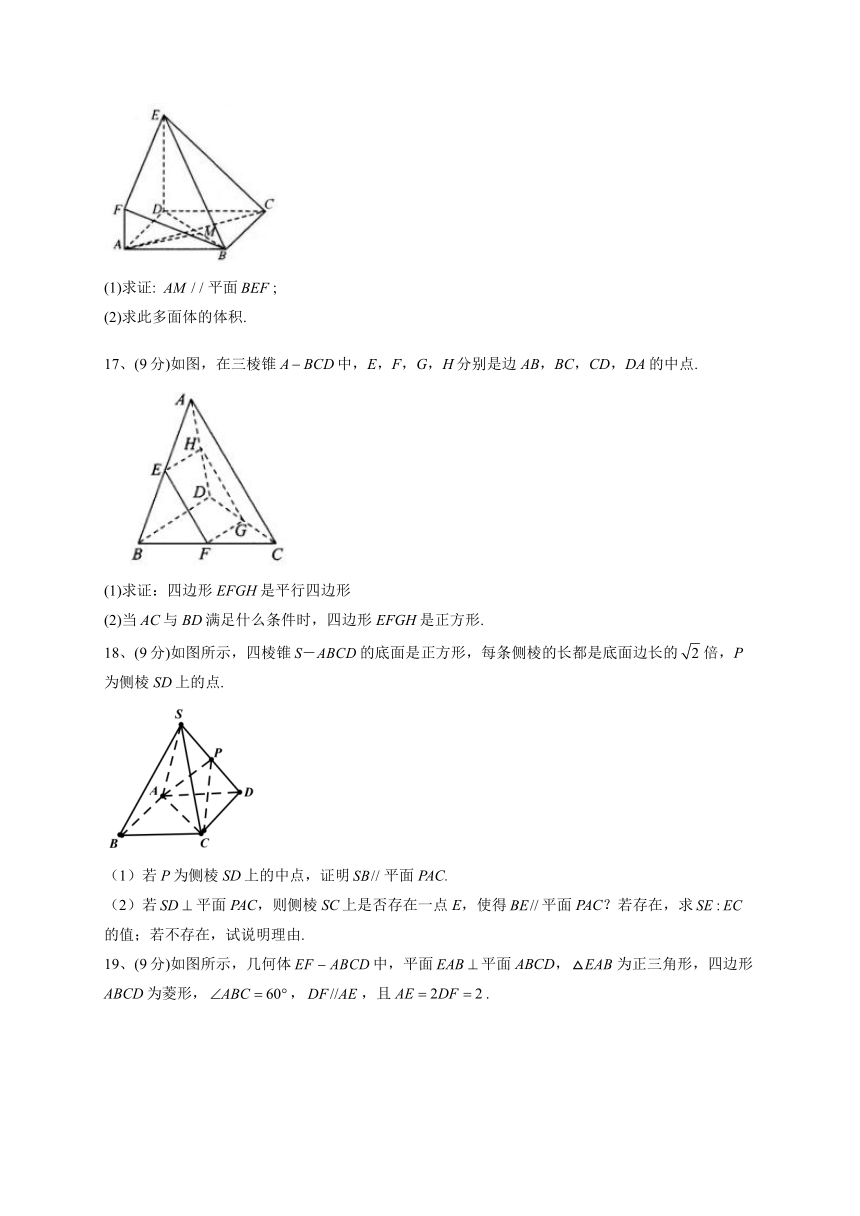
17、(9分)如图,在三棱锥中,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)求证:四边形EFGH是平行四边形
(2)当AC与BD满足什么条件时,四边形EFGH是正方形.
18、(9分)如图所示,四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.
(1)若P为侧棱SD上的中点,证明平面PAC.
(2)若平面PAC,则侧棱SC上是否存在一点E,使得平面PAC?若存在,求的值;若不存在,试说明理由.
19、(9分)如图所示,几何体中,平面平面ABCD,为正三角形,四边形ABCD为菱形,,,且.
(1)证明:平面CEF;
(2)求四棱锥的体积.
参考答案
1、答案:B
解析:
2、答案:C
解析:
3、答案:C
解析:
4、答案:A
解析:
5、答案:A
解析:
6、答案:B
解析:
7、答案:C
解析:
8、答案:C
解析:
9、答案:C
解析:由直线平面,直线,可得直线a,b一定没有公共点,故两直线的位置关系可以是异面或平行.故选C.
10、答案:A
解析:如图,取的中点N,连接MN,AN,AC,CM,,则四边形MNAC为所求图形.因为,所以四边形为平行四边形,所以.又M,N分别为,的中点,所以,故,且,所以四边形MNAC为梯形,.过点M作交AC于点P.因为,所以.在中,,所以梯形MNAC的面积为.故选A.
11、答案:线段
解析:
12、答案:
解析:当E为SA的中点时,连接AC,
设AC与BD的交点为O,连接EO.
因为四边形ABCD是平行四边形,
所以点O是AC的中点.
又E是SA的中点,所以OE是的中位线.
所以.
因为平面EBD,平面EBD,
所以平面EBD.
13、答案:1
解析:连接正方体各面上的对角线.
过点和A点的对角线和直线是相交.
分别与是异面直线,夹角为60°,和是垂直的.
故只有直线.
故满足条件的直线只有1条.
14、答案:相交
解析:连接PQ,,.点P,Q分别是,的中点,.在正方体中,易知,,,D,Q,P共面.又,四边形是梯形,直线与DQ相交.
15、答案:相交;平行
解析:是的中点,直线DM与直线相交,与平面有一个公共点,与平面相交.取的中点,连接,.,,.,,.四边形为平行四边形,,平面.
16、答案:(1)见解析(2)
解析:(1) 证明: 过点 作, 交 于点, 则
因为, 所以, 且, 所以四边形 为平行四边形,所以. 又 平面 丈平面, 所以 平面.
(2) 因为 平面 平面, 所以, 因为, 所以 平面.
所以, ,
即此多面体的体积为
17、答案:(1)见解析.
(2).
解析:(1)在中,E,F分别是边AB,BC的中点,
所以,且,
同理有,且,
所以且,
故四边形EFGH是平行四边形.
(2)当AC与BD垂直且相等时,四边形EFGH是正方形,理由如下:
若,则有,
又因为四边形EFGH是平行四边形,
所以四边形EFGH是菱形.
若,则,所以菱形EFGH是正方形.
18、答案:(1)证明过程见解析.
(2)棱SC上存在一点E使平面PAC.
解析:(1)证明:连接BD,设AC交BD于O,则O是DB的中点,P为侧棱DS上的中点,
得,所以平面PAC.
(2)棱SC上存在一点E使平面PAC.理由如下:
以O为坐标原点,,,分别为x轴、y轴、z轴正方向,建立空间直角坐标系如图.
设底面边长为a,则高,
于是,,,,
由已知条件知是平面PAC的一个法向量,
且,,.
设,则,
由.
即当时,.
又BE不在平面PAC内,故平面PAC.
19、答案:(1)连接AC交BD于点O,则O为AC中点,
取CE中点G,连接GO,GF,
则,又,则,
则四边形ODFG为平行四边形,故,
又平面CEF,平面CEF,
所以平面CEF.
(2)因为,,,,
所以平面平面EAB,且,
又平面平面ABCD,所以平面平面ABCD,
作,平面平面,则平面ABCD,
因为,,
所以,,
故四棱锥的体积为.
解析:
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)如图,在棱长为1的正方体中,M,N分别是的中点,过直线BD的平面平面AMN,则平面截该正方体所得截面的面积为( )
A. B. C. D.
2、(4分)已知平面平面,直线,直线,下列结论中不正确的是( )
A. B.
C. D.m与n不相交
3、(4分)如图,在正方体中,M,N,P分别是的中点,则下列结论正确的是( )
A. B.
C.平面 D.平面BDP
4、(4分)已知平面平面,过平面内的一条直线a的平面,与平面相交,交线为直线b,则a,b的位置关系是( )
A.平行 B.相交 C.异面 D.不确定
5、(4分)下列命题中不正确的是( )
A.平面平面,一条直线a平行于平面,则a一定平行于平面
B.平面平面,则平面内的任意一条直线都平行于平面
C.一个三角形有两条边所在的直线分别平行于一个平面,那么该三角形所在的平面与这个平面平行
D.分别在两个平行平面内的两条直线只能是平行直线或异面直线
6、(4分)在三棱锥中,E,F分别为SB,SC上的点,且平面ABC,则( )
A.EF与BC相交 B.
C.EF与BC异面 D.以上均有可能
7、(4分)如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH在原正方体中互为异面的对数为( )
A.1 B.2 C.3 D.4
8、(4分)已知平面平面,若P,Q是之间的两个点,则( )
A.过P,Q的平面一定与都相交
B.过P,Q有且仅有一个平面与都平行
C.过P,Q的平面不一定与都平行
D.过P,Q可作无数个平面与都平行
9、(4分)若直线平面,直线,则直线a与b的位置关系是( )
A.相交 B.异面 C.异面或平行 D.平行
10、(4分)如图,在长方体中,,,E,F,M分别为,,的中点,过点M的平面与平面DEF平行,且与长方体的面相交,则交线围成的平面图形的面积为( )
A. B. C.12 D.24
二、填空题(共25分)
11、(5分)如图,在正方体中,M,N,P分别是的中点,点H在四边形的边及其内部运动,则H满足条件________时,有平面MNP.
12、(5分)若在四棱锥中,底面ABCD为平行四边形,E是SA上的一点,当点E满足条件________时,平面EBD.
13、(5分)在正方体中,与平行的面上的对角线有___________条.
14、(5分)如图,在正方体中,点P,Q分别是,的中点,则直线与DQ的位置关系是___________________.(填“平行”“相交”或“异面”)
15、(5分)如图,在正方体中,M是的中点,则直线DM与平面的位置关系是____________,直线DM与平面的位置关系是_______________.
三、解答题(共35分)
16、(8分)如图所示多面体中, 底面 是边长为 3 的正方形, 上平面 是 上一点,.
(1)求证: 平面;
(2)求此多面体的体积.
17、(9分)如图,在三棱锥中,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)求证:四边形EFGH是平行四边形
(2)当AC与BD满足什么条件时,四边形EFGH是正方形.
18、(9分)如图所示,四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.
(1)若P为侧棱SD上的中点,证明平面PAC.
(2)若平面PAC,则侧棱SC上是否存在一点E,使得平面PAC?若存在,求的值;若不存在,试说明理由.
19、(9分)如图所示,几何体中,平面平面ABCD,为正三角形,四边形ABCD为菱形,,,且.
(1)证明:平面CEF;
(2)求四棱锥的体积.
参考答案
1、答案:B
解析:
2、答案:C
解析:
3、答案:C
解析:
4、答案:A
解析:
5、答案:A
解析:
6、答案:B
解析:
7、答案:C
解析:
8、答案:C
解析:
9、答案:C
解析:由直线平面,直线,可得直线a,b一定没有公共点,故两直线的位置关系可以是异面或平行.故选C.
10、答案:A
解析:如图,取的中点N,连接MN,AN,AC,CM,,则四边形MNAC为所求图形.因为,所以四边形为平行四边形,所以.又M,N分别为,的中点,所以,故,且,所以四边形MNAC为梯形,.过点M作交AC于点P.因为,所以.在中,,所以梯形MNAC的面积为.故选A.
11、答案:线段
解析:
12、答案:
解析:当E为SA的中点时,连接AC,
设AC与BD的交点为O,连接EO.
因为四边形ABCD是平行四边形,
所以点O是AC的中点.
又E是SA的中点,所以OE是的中位线.
所以.
因为平面EBD,平面EBD,
所以平面EBD.
13、答案:1
解析:连接正方体各面上的对角线.
过点和A点的对角线和直线是相交.
分别与是异面直线,夹角为60°,和是垂直的.
故只有直线.
故满足条件的直线只有1条.
14、答案:相交
解析:连接PQ,,.点P,Q分别是,的中点,.在正方体中,易知,,,D,Q,P共面.又,四边形是梯形,直线与DQ相交.
15、答案:相交;平行
解析:是的中点,直线DM与直线相交,与平面有一个公共点,与平面相交.取的中点,连接,.,,.,,.四边形为平行四边形,,平面.
16、答案:(1)见解析(2)
解析:(1) 证明: 过点 作, 交 于点, 则
因为, 所以, 且, 所以四边形 为平行四边形,所以. 又 平面 丈平面, 所以 平面.
(2) 因为 平面 平面, 所以, 因为, 所以 平面.
所以, ,
即此多面体的体积为
17、答案:(1)见解析.
(2).
解析:(1)在中,E,F分别是边AB,BC的中点,
所以,且,
同理有,且,
所以且,
故四边形EFGH是平行四边形.
(2)当AC与BD垂直且相等时,四边形EFGH是正方形,理由如下:
若,则有,
又因为四边形EFGH是平行四边形,
所以四边形EFGH是菱形.
若,则,所以菱形EFGH是正方形.
18、答案:(1)证明过程见解析.
(2)棱SC上存在一点E使平面PAC.
解析:(1)证明:连接BD,设AC交BD于O,则O是DB的中点,P为侧棱DS上的中点,
得,所以平面PAC.
(2)棱SC上存在一点E使平面PAC.理由如下:
以O为坐标原点,,,分别为x轴、y轴、z轴正方向,建立空间直角坐标系如图.
设底面边长为a,则高,
于是,,,,
由已知条件知是平面PAC的一个法向量,
且,,.
设,则,
由.
即当时,.
又BE不在平面PAC内,故平面PAC.
19、答案:(1)连接AC交BD于点O,则O为AC中点,
取CE中点G,连接GO,GF,
则,又,则,
则四边形ODFG为平行四边形,故,
又平面CEF,平面CEF,
所以平面CEF.
(2)因为,,,,
所以平面平面EAB,且,
又平面平面ABCD,所以平面平面ABCD,
作,平面平面,则平面ABCD,
因为,,
所以,,
故四棱锥的体积为.
解析:
