2022-2023学年人教B版2019必修四11.4空间中的垂直关系 同步课时训练(Word版含解析)
文档属性
| 名称 | 2022-2023学年人教B版2019必修四11.4空间中的垂直关系 同步课时训练(Word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 657.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 11:51:05 | ||
图片预览


文档简介
11.4空间中的垂直关系 同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
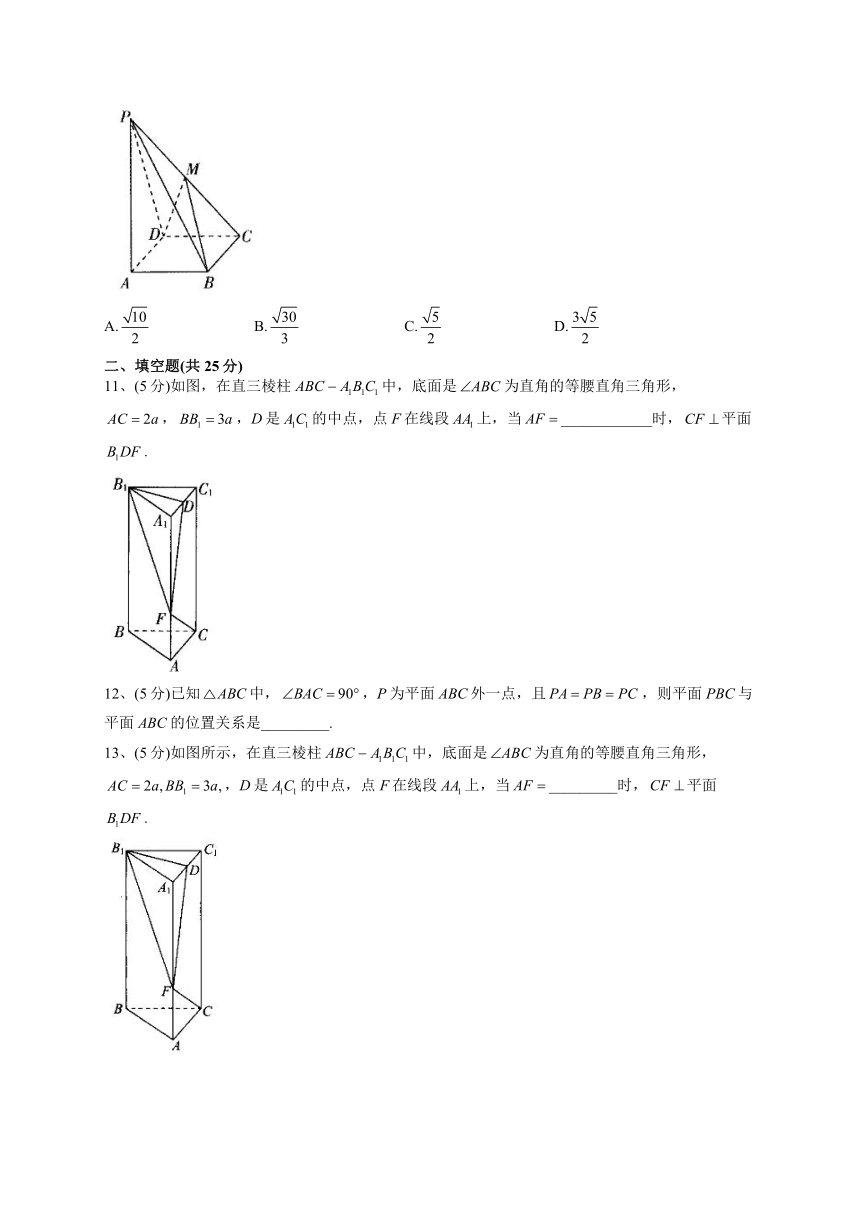
1、(4分)如图,正方形中,E,F分别是的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使三点重合,重合后的点记为G,则在四面体中必有( )
A.平面EFG B.平面EFG
C.平面SEF D.平面SEF
2、(4分)如图所示,在四边形ABCD中,,将沿BD折起,使平面平面BCD,连接AC,则下列命题正确的是( )
A.平面平面ABC B.平面平面BDC
C.平面平面BDC D.平面平面ABC
3、(4分)已知平面平面,点,则过点A且垂直于平面的直线( )
A.只有一条,不一定在平面内
B.有无数条,不一定在平面内
C.只有一条,一定在平面内
D.有无数条,一定在平面内
4、(4分)下列说法中,正确的是( )
A.垂直于同一直线的两条直线互相平行
B.平行于同一平面的两个平面平行
C.垂直于同一平面的两个平面互相平行
D.平行于同一平面的两条直线互相平行
5、(4分)已知直线a,b与平面,下列能使成立的条件是( )
A.
B.
C.
D.
6、(4分)如图,设平面平面平面平面,垂足分别为G,H.为使,则需增加的一个条件是( )
A.平面 B.平面
C. D.
7、(4分)如果一条直线垂直于一个平面内的下列各种情况,能保证该直线与平面垂直的是( )
①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边.
A.①③ B.② C.②④ D.①②④
8、(4分)在四边形ABCD中,,,,.如图,将沿BD折起,使平面平面BCD,构成三棱锥.则在三棱锥中,下列结论正确的是( )
A.平面平面ABC B.平面平面BDC
C.平面平面BDC D.平面平面ABC
9、(4分)在空间四边形ABCD中,若,,则有( )
A.平面平面ADC B.平面平面ADB
C.平面平面DBC D.平面平面DBC
10、(4分)如图,在四棱雉中,底面ABCD,底面ABCD为正方形,且,M为PC上一动点.若,则MB的长度为( )
A. B. C. D.
二、填空题(共25分)
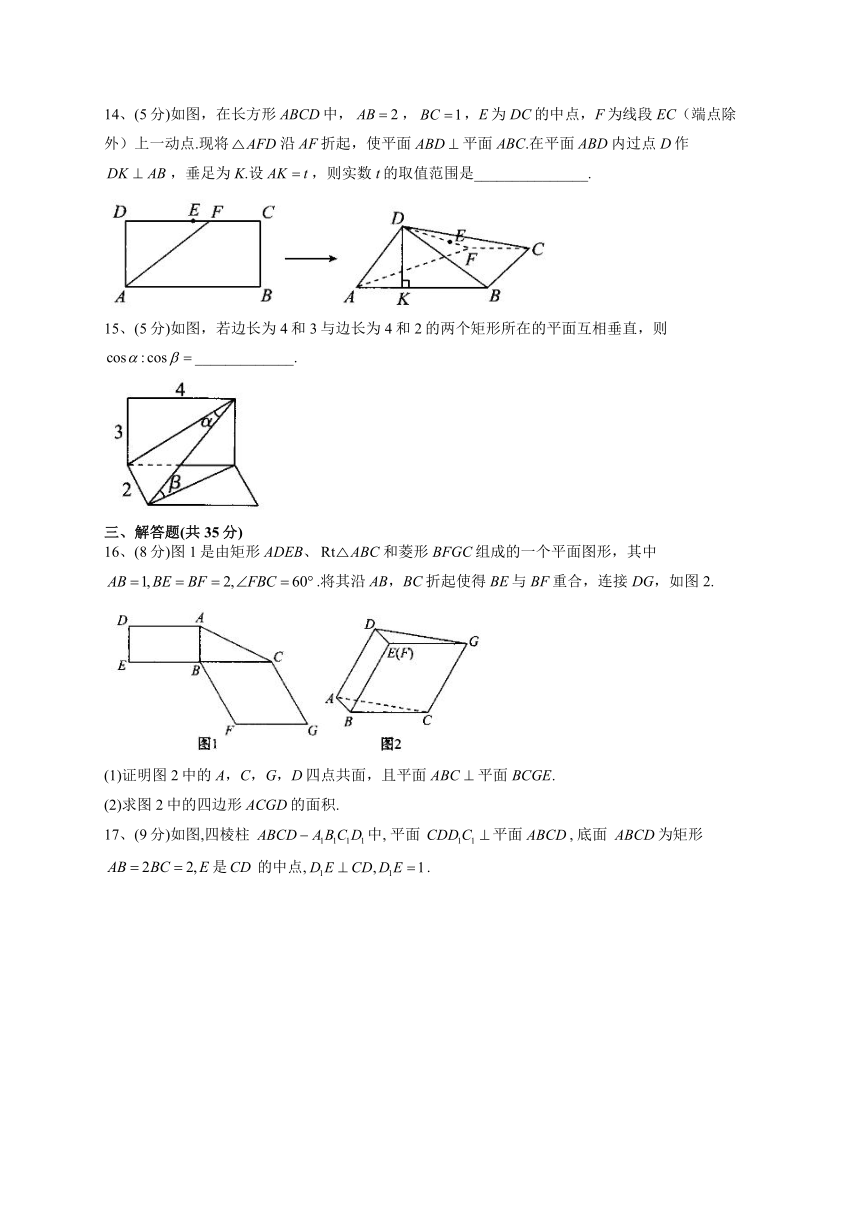
11、(5分)如图,在直三棱柱中,底面是为直角的等腰直角三角形,,,D是的中点,点F在线段上,当____________时,平面.
12、(5分)已知中,,P为平面ABC外一点,且,则平面PBC与平面ABC的位置关系是_________.
13、(5分)如图所示,在直三棱柱中,底面是为直角的等腰直角三角形,,D是的中点,点F在线段上,当_________时,平面.
14、(5分)如图,在长方形ABCD中,,,E为DC的中点,F为线段EC(端点除外)上一动点.现将沿AF折起,使平面平面ABC.在平面ABD内过点D作,垂足为K.设,则实数t的取值范围是_______________.
15、(5分)如图,若边长为4和3与边长为4和2的两个矩形所在的平面互相垂直,则_____________.
三、解答题(共35分)
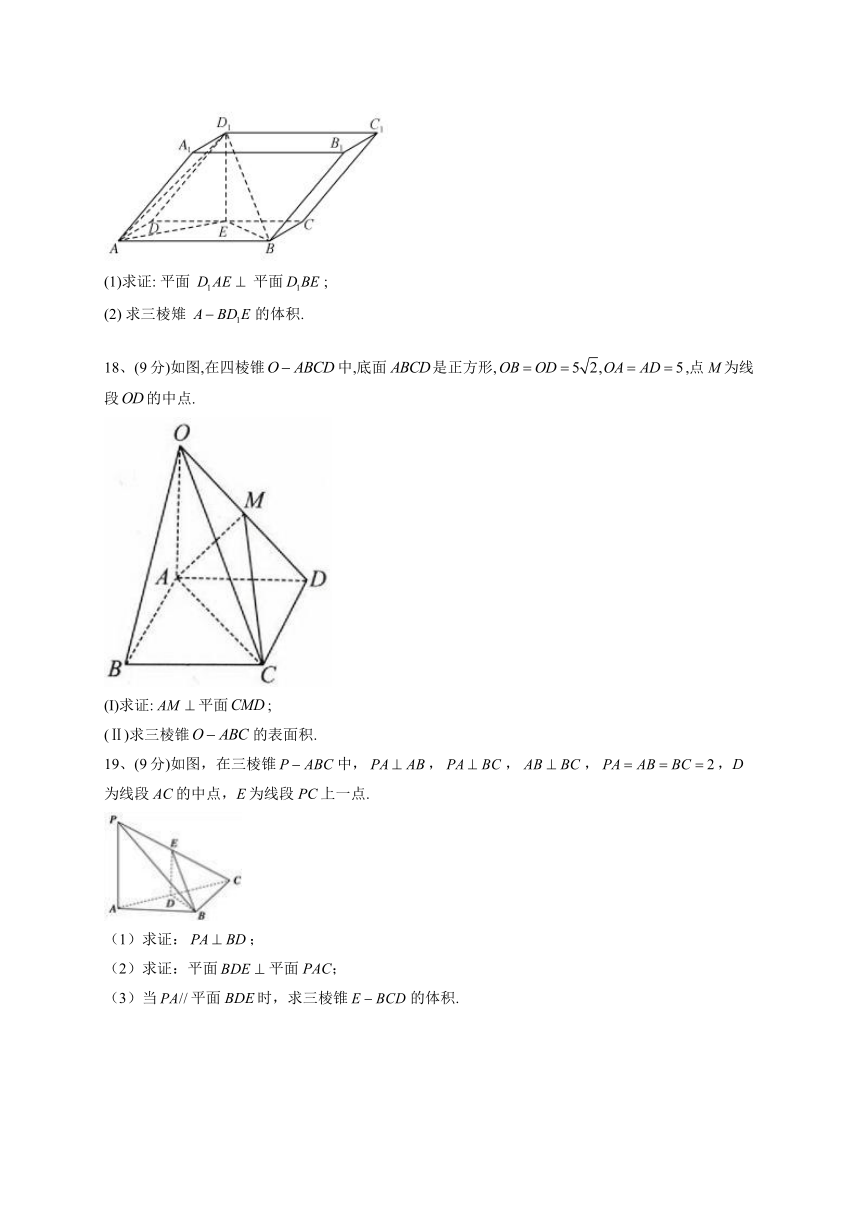
16、(8分)图1是由矩形ADEB、和菱形BFGC组成的一个平面图形,其中.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
(1)证明图2中的A,C,G,D四点共面,且平面平面BCGE.
(2)求图2中的四边形ACGD的面积.
17、(9分)如图,四棱柱 中, 平面 平面, 底面 为矩形 是 的中点,.
(1)求证: 平面 平面;
(2) 求三棱雉 的体积.
18、(9分)如图,在四棱锥中,底面是正方形,,点M为线段的中点.
(I)求证:平面;
(Ⅱ)求三棱锥的表面积.
19、(9分)如图,在三棱锥中,,,,,D为线段AC的中点,E为线段PC上一点.
(1)求证:;
(2)求证:平面平面PAC;
(3)当平面BDE时,求三棱锥的体积.
参考答案
1、答案:A
解析:
2、答案:D
解析:
3、答案:C
解析:
4、答案:B
解析:
5、答案:D
解析:
6、答案:B
解析:
7、答案:A
解析:
8、答案:D
解析:在平面图形中,,折起后仍然满足.因为平面平面BCD,所以平面ABD,.又因为,所以平面ADC,所以平面平面ABC.
9、答案:D
解析:,,,平面DBC.
又平面ADC,平面平面DBC.
10、答案:B
解析:如图所示,连接AC,BD.因为底面ABCD为正方形,所以.又因为底面ABCD,平面ABCD,所以.因为,平面PAC,平面PAC,所以平面PAC.因为平面PAC,所以.因为,,平面BDM,平面BDM,所以平面BDM.又因为平面BDM,所以.因为底面ABCD为正方体,所以.又底面ABCD,平面ABCD,所以.因为,平面PAB,平面PAB,所以平面PAB.又因为平面PAB,所以.在中,,,所以.在中,.又,所以.
11、答案:a或2a
解析:由已知得是等腰直角三角形,,D是的中点,.平面平面,平面平面,平面.又平面,.若平面,则.设,则,,,,解得或2a.
12、答案:平面平面ABC
解析:因为,所以P在所在平面上的射影必落在的外心上,
又的外心为BC的中点,设为O,则平面ABC,
又平面PBC,所以平面平面ABC.
13、答案:a或
解析:由已知得平面,
又平面,所以,
故若平面,则必有.
设,则,
又,
所以,
解得或.
14、答案:
解析:过点K作于点M,连接DM.平面平面ABC,平面平面,,平面ABD,平面ABC.平面ABC,.,,平面DMK.平面DMK,.与折前的图形对比,可知折前的图形中D,M,K三点共线,且,,,即,.,.
15、答案:
解析:由题意,得两个矩形的对角线长分别为5,,
所以,,
所以.
16、答案:(1)见解析.
(2)面积为4.
解析:(1)由已知得,
所以,故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得,故平面BCGE.
又因为平面ABC,所以平面平面BCGE.
(2)取CG的中点M,连接EM,DM.
因为平面BCGE,
所以平面BCGE,故.
由已知,四边形BCGE是菱形且得,
故平面DEM.
因此.
在中,,故.
所以四边形ACGD的面积为4.
17、答案:(1)见解析(2)
解析:(1)证明: 因为平面 平面, 平面 平面,
所以 平面.
因为 平面, 所以.
又在矩形 中, 是 的中点,
所以, 所以.
又, 所以 平面.
因为 平面, 所以平面 平面.
(2) 由 (1) 知 平面, 所以 即为点 到平面 的距离,
所以.
18、答案:(I)见解析
(Ⅱ)
解析:(I)证明:由,可得,则由勾股定理的逆定理可得,同理可得.
又,
所以平面.
又平面,
所以.
又四边形是正方形,
所以.
又,
所以平面.
因为平面,
所以.
又M为的中点,,
所以.
又,
所以平面,
即平面.
(Ⅱ)易知,
且,
,
,
所以三棱锥的表面积
.
19、答案:(1)证明过程见解析.
(2)证明过程见解析.
(3)体积为.
解析:(1)证明:因为,,所以平面ABC,
又因为平面ABC,所以.
(2)因为,D为AC中点,所以,
由(1)知,,所以平面PAC.
所以平面平面PAC.
(3)因为平面BDE,平面平面,
所以.
因为D为AC的中点,所以,.
由(1)知,平面ABC,所以平面PAC.
所以三棱锥的体积.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)如图,正方形中,E,F分别是的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使三点重合,重合后的点记为G,则在四面体中必有( )
A.平面EFG B.平面EFG
C.平面SEF D.平面SEF
2、(4分)如图所示,在四边形ABCD中,,将沿BD折起,使平面平面BCD,连接AC,则下列命题正确的是( )
A.平面平面ABC B.平面平面BDC
C.平面平面BDC D.平面平面ABC
3、(4分)已知平面平面,点,则过点A且垂直于平面的直线( )
A.只有一条,不一定在平面内
B.有无数条,不一定在平面内
C.只有一条,一定在平面内
D.有无数条,一定在平面内
4、(4分)下列说法中,正确的是( )
A.垂直于同一直线的两条直线互相平行
B.平行于同一平面的两个平面平行
C.垂直于同一平面的两个平面互相平行
D.平行于同一平面的两条直线互相平行
5、(4分)已知直线a,b与平面,下列能使成立的条件是( )
A.
B.
C.
D.
6、(4分)如图,设平面平面平面平面,垂足分别为G,H.为使,则需增加的一个条件是( )
A.平面 B.平面
C. D.
7、(4分)如果一条直线垂直于一个平面内的下列各种情况,能保证该直线与平面垂直的是( )
①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边.
A.①③ B.② C.②④ D.①②④
8、(4分)在四边形ABCD中,,,,.如图,将沿BD折起,使平面平面BCD,构成三棱锥.则在三棱锥中,下列结论正确的是( )
A.平面平面ABC B.平面平面BDC
C.平面平面BDC D.平面平面ABC
9、(4分)在空间四边形ABCD中,若,,则有( )
A.平面平面ADC B.平面平面ADB
C.平面平面DBC D.平面平面DBC
10、(4分)如图,在四棱雉中,底面ABCD,底面ABCD为正方形,且,M为PC上一动点.若,则MB的长度为( )
A. B. C. D.
二、填空题(共25分)
11、(5分)如图,在直三棱柱中,底面是为直角的等腰直角三角形,,,D是的中点,点F在线段上,当____________时,平面.
12、(5分)已知中,,P为平面ABC外一点,且,则平面PBC与平面ABC的位置关系是_________.
13、(5分)如图所示,在直三棱柱中,底面是为直角的等腰直角三角形,,D是的中点,点F在线段上,当_________时,平面.
14、(5分)如图,在长方形ABCD中,,,E为DC的中点,F为线段EC(端点除外)上一动点.现将沿AF折起,使平面平面ABC.在平面ABD内过点D作,垂足为K.设,则实数t的取值范围是_______________.
15、(5分)如图,若边长为4和3与边长为4和2的两个矩形所在的平面互相垂直,则_____________.
三、解答题(共35分)
16、(8分)图1是由矩形ADEB、和菱形BFGC组成的一个平面图形,其中.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
(1)证明图2中的A,C,G,D四点共面,且平面平面BCGE.
(2)求图2中的四边形ACGD的面积.
17、(9分)如图,四棱柱 中, 平面 平面, 底面 为矩形 是 的中点,.
(1)求证: 平面 平面;
(2) 求三棱雉 的体积.
18、(9分)如图,在四棱锥中,底面是正方形,,点M为线段的中点.
(I)求证:平面;
(Ⅱ)求三棱锥的表面积.
19、(9分)如图,在三棱锥中,,,,,D为线段AC的中点,E为线段PC上一点.
(1)求证:;
(2)求证:平面平面PAC;
(3)当平面BDE时,求三棱锥的体积.
参考答案
1、答案:A
解析:
2、答案:D
解析:
3、答案:C
解析:
4、答案:B
解析:
5、答案:D
解析:
6、答案:B
解析:
7、答案:A
解析:
8、答案:D
解析:在平面图形中,,折起后仍然满足.因为平面平面BCD,所以平面ABD,.又因为,所以平面ADC,所以平面平面ABC.
9、答案:D
解析:,,,平面DBC.
又平面ADC,平面平面DBC.
10、答案:B
解析:如图所示,连接AC,BD.因为底面ABCD为正方形,所以.又因为底面ABCD,平面ABCD,所以.因为,平面PAC,平面PAC,所以平面PAC.因为平面PAC,所以.因为,,平面BDM,平面BDM,所以平面BDM.又因为平面BDM,所以.因为底面ABCD为正方体,所以.又底面ABCD,平面ABCD,所以.因为,平面PAB,平面PAB,所以平面PAB.又因为平面PAB,所以.在中,,,所以.在中,.又,所以.
11、答案:a或2a
解析:由已知得是等腰直角三角形,,D是的中点,.平面平面,平面平面,平面.又平面,.若平面,则.设,则,,,,解得或2a.
12、答案:平面平面ABC
解析:因为,所以P在所在平面上的射影必落在的外心上,
又的外心为BC的中点,设为O,则平面ABC,
又平面PBC,所以平面平面ABC.
13、答案:a或
解析:由已知得平面,
又平面,所以,
故若平面,则必有.
设,则,
又,
所以,
解得或.
14、答案:
解析:过点K作于点M,连接DM.平面平面ABC,平面平面,,平面ABD,平面ABC.平面ABC,.,,平面DMK.平面DMK,.与折前的图形对比,可知折前的图形中D,M,K三点共线,且,,,即,.,.
15、答案:
解析:由题意,得两个矩形的对角线长分别为5,,
所以,,
所以.
16、答案:(1)见解析.
(2)面积为4.
解析:(1)由已知得,
所以,故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得,故平面BCGE.
又因为平面ABC,所以平面平面BCGE.
(2)取CG的中点M,连接EM,DM.
因为平面BCGE,
所以平面BCGE,故.
由已知,四边形BCGE是菱形且得,
故平面DEM.
因此.
在中,,故.
所以四边形ACGD的面积为4.
17、答案:(1)见解析(2)
解析:(1)证明: 因为平面 平面, 平面 平面,
所以 平面.
因为 平面, 所以.
又在矩形 中, 是 的中点,
所以, 所以.
又, 所以 平面.
因为 平面, 所以平面 平面.
(2) 由 (1) 知 平面, 所以 即为点 到平面 的距离,
所以.
18、答案:(I)见解析
(Ⅱ)
解析:(I)证明:由,可得,则由勾股定理的逆定理可得,同理可得.
又,
所以平面.
又平面,
所以.
又四边形是正方形,
所以.
又,
所以平面.
因为平面,
所以.
又M为的中点,,
所以.
又,
所以平面,
即平面.
(Ⅱ)易知,
且,
,
,
所以三棱锥的表面积
.
19、答案:(1)证明过程见解析.
(2)证明过程见解析.
(3)体积为.
解析:(1)证明:因为,,所以平面ABC,
又因为平面ABC,所以.
(2)因为,D为AC中点,所以,
由(1)知,,所以平面PAC.
所以平面平面PAC.
(3)因为平面BDE,平面平面,
所以.
因为D为AC的中点,所以,.
由(1)知,平面ABC,所以平面PAC.
所以三棱锥的体积.
