人教版八年级上册11.3.3多边形的外角和课件(共14张PPT)
文档属性
| 名称 | 人教版八年级上册11.3.3多边形的外角和课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 491.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 08:30:22 | ||
图片预览


文档简介
(共14张PPT)
多边形的外角和
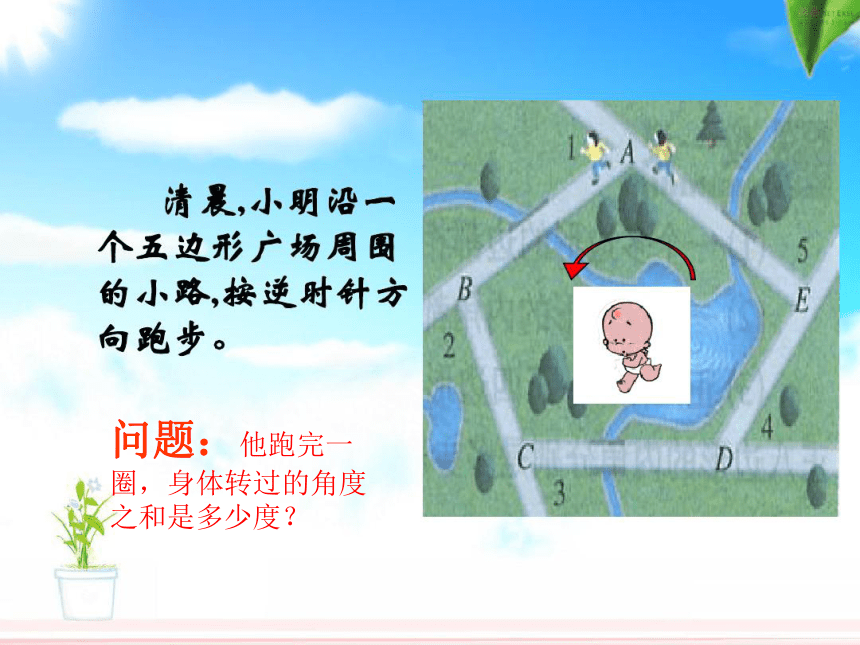
问题:他跑完一圈,身体转过的角度之和是多少度?
1.了解多边形外角和的概念。
2.掌握多边形的外角和公式,并能灵活的运用多边形外角和公式解决有关问题。
3.让学生经历探索多边形外角和公式的过程,培养学生主动探究的习惯。
学习目标
A
B
C
D
E
4
5
1
2
3
6
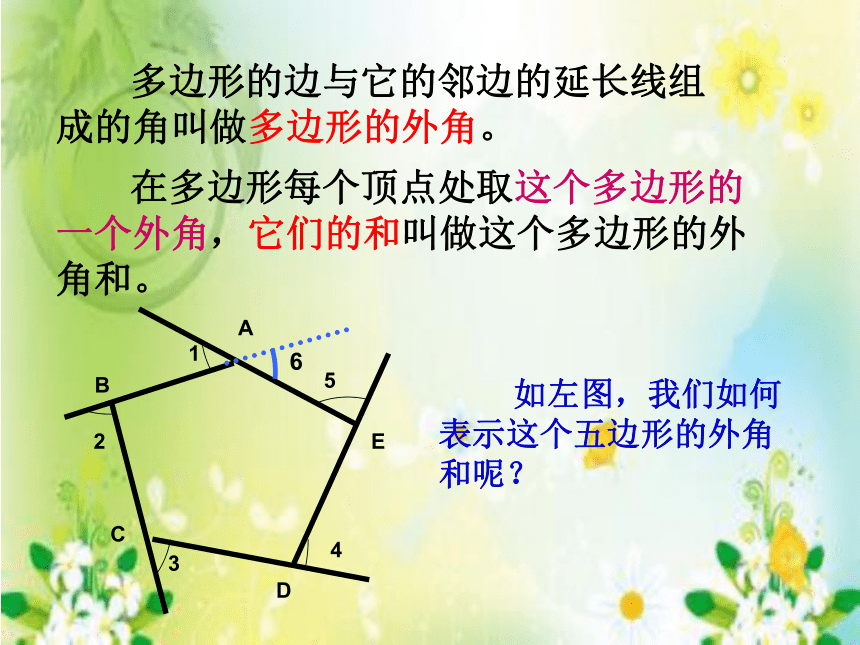
在多边形每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
多边形的边与它的邻边的延长线组成的角叫做多边形的外角。
如左图,我们如何表示这个五边形的外角和呢?
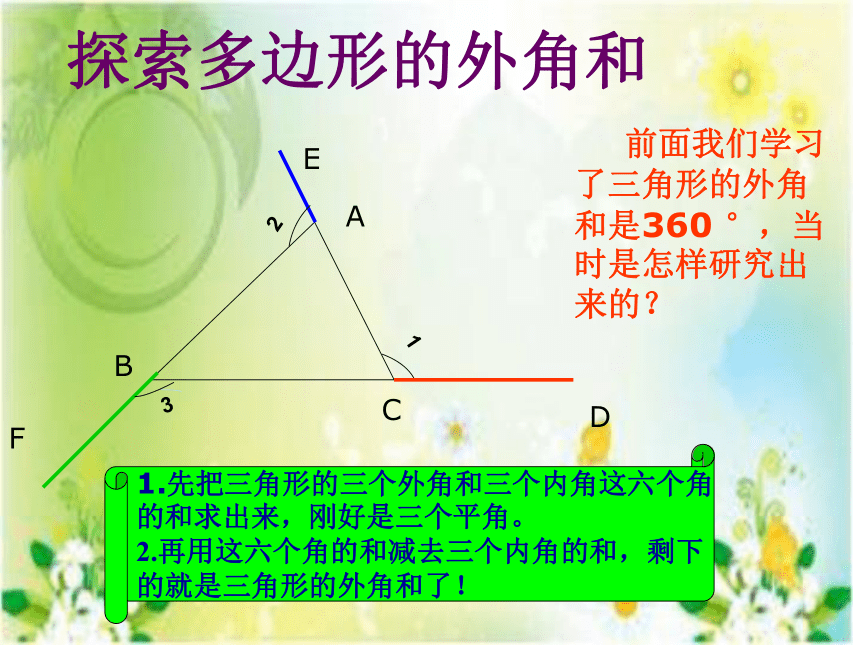
前面我们学习了三角形的外角和是360 °,当时是怎样研究出来的?
A
B
C
D
E
F
1.先把三角形的三个外角和三个内角这六个角
的和求出来,刚好是三个平角。
2.再用这六个角的和减去三个内角的和,剩下
的就是三角形的外角和了!
探索多边形的外角和
2
1
3
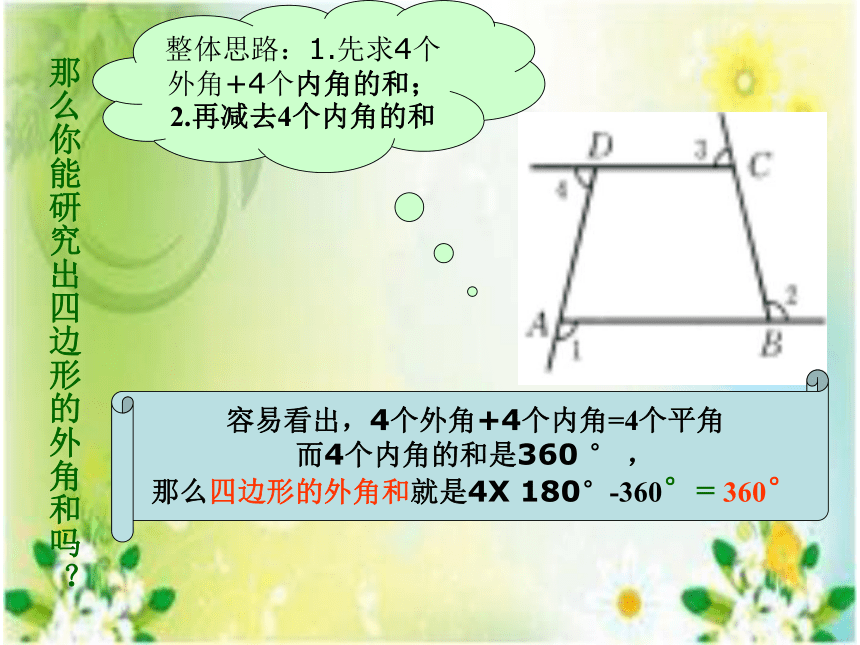
那么你能研究出四边形的外角和吗?
整体思路:1.先求4个外角+4个内角的和;
2.再减去4个内角的和
容易看出,4个外角+4个内角=4个平角
而4个内角的和是360 ° ,
那么四边形的外角和就是4X 180°-360°= 360°
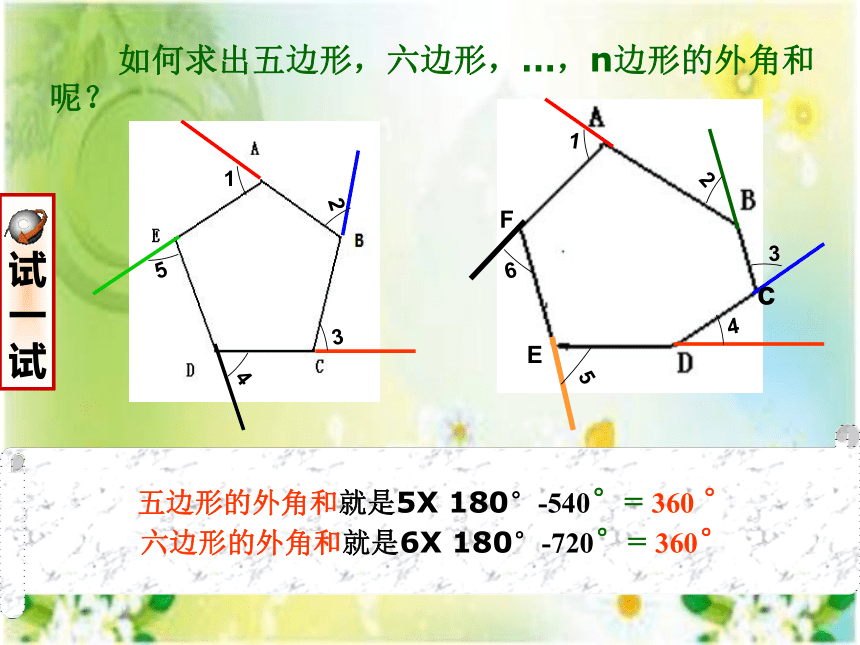
如何求出五边形,六边形,…,n边形的外角和呢?
五边形的外角和就是5X 180°-540°= 360 °
六边形的外角和就是6X 180°-720°= 360°
c
E
F
试一试
1
2
3
4
5
1
2
6
5
4
3
多边形 图形 多边形的外角和
三角形
四边形
五边形
六边形
n边形
3×180o-(3-2)×180o=360o
4×180o-(4-2)×180o=360o
5×180o-(5-2)×180o=360o
6×180o-(6-2)×180o=360o
n×180o-(n-2)×180o=360o
合作学习
多边形的外角和
多边形的外角和公式
多边形的外角和等于360°
结论
解: 设这个多边形的边数为n,
则它的内角和等于 (n-2) ×180°,
外角和等于360 ,所以
(n-2) ×180= 3×360
n = 8
这个多边形的边数为8.
例题讲解
例1:一个多边形的内角和等于它的外角和的3倍,它是几边形?
例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
例题讲解
1.若一个多边形的每一个外角都等于15°,则这个多边形的边数是________。
2.若一个十边形的每个外角都相等,则它的
每个外角的度数为________度,每个内角的
度数为________度。
3.若一个多边形的内角和等于它的外角和,
则它的边数是_______。
4.多边形的边数增加1,则内角和增加
_____度,外角和增加_____度。
24
36
144
4
180
0
巩固练习
这节课你收获了什么?
1 、多边形的外角及外角和定义
2 、多边形的外角和公式:多边形的外角和等于360°
3、多边形外角和的推理过程
4、我们还学会了运用多边形外角和公式进行相关计算
课堂小结
课外作业:
习题 11.3
P25 6
多边形的外角和
问题:他跑完一圈,身体转过的角度之和是多少度?
1.了解多边形外角和的概念。
2.掌握多边形的外角和公式,并能灵活的运用多边形外角和公式解决有关问题。
3.让学生经历探索多边形外角和公式的过程,培养学生主动探究的习惯。
学习目标
A
B
C
D
E
4
5
1
2
3
6
在多边形每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
多边形的边与它的邻边的延长线组成的角叫做多边形的外角。
如左图,我们如何表示这个五边形的外角和呢?
前面我们学习了三角形的外角和是360 °,当时是怎样研究出来的?
A
B
C
D
E
F
1.先把三角形的三个外角和三个内角这六个角
的和求出来,刚好是三个平角。
2.再用这六个角的和减去三个内角的和,剩下
的就是三角形的外角和了!
探索多边形的外角和
2
1
3
那么你能研究出四边形的外角和吗?
整体思路:1.先求4个外角+4个内角的和;
2.再减去4个内角的和
容易看出,4个外角+4个内角=4个平角
而4个内角的和是360 ° ,
那么四边形的外角和就是4X 180°-360°= 360°
如何求出五边形,六边形,…,n边形的外角和呢?
五边形的外角和就是5X 180°-540°= 360 °
六边形的外角和就是6X 180°-720°= 360°
c
E
F
试一试
1
2
3
4
5
1
2
6
5
4
3
多边形 图形 多边形的外角和
三角形
四边形
五边形
六边形
n边形
3×180o-(3-2)×180o=360o
4×180o-(4-2)×180o=360o
5×180o-(5-2)×180o=360o
6×180o-(6-2)×180o=360o
n×180o-(n-2)×180o=360o
合作学习
多边形的外角和
多边形的外角和公式
多边形的外角和等于360°
结论
解: 设这个多边形的边数为n,
则它的内角和等于 (n-2) ×180°,
外角和等于360 ,所以
(n-2) ×180= 3×360
n = 8
这个多边形的边数为8.
例题讲解
例1:一个多边形的内角和等于它的外角和的3倍,它是几边形?
例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
例题讲解
1.若一个多边形的每一个外角都等于15°,则这个多边形的边数是________。
2.若一个十边形的每个外角都相等,则它的
每个外角的度数为________度,每个内角的
度数为________度。
3.若一个多边形的内角和等于它的外角和,
则它的边数是_______。
4.多边形的边数增加1,则内角和增加
_____度,外角和增加_____度。
24
36
144
4
180
0
巩固练习
这节课你收获了什么?
1 、多边形的外角及外角和定义
2 、多边形的外角和公式:多边形的外角和等于360°
3、多边形外角和的推理过程
4、我们还学会了运用多边形外角和公式进行相关计算
课堂小结
课外作业:
习题 11.3
P25 6
