初中数学人教版九年级上册 24.4 第1课时 弧长和扇形面积 教案+课时作业(Word版,含答案)
文档属性
| 名称 | 初中数学人教版九年级上册 24.4 第1课时 弧长和扇形面积 教案+课时作业(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 689.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 11:44:08 | ||
图片预览


文档简介
24.4 弧长和扇形面积(第1课时)
一、教学内容
1.n°的圆心角所对的弧长L=
2.扇形的概念;
3.圆心角为n°的扇形面积是S扇形=;
4.应用以上内容解决一些具体题目.
二、教学目标
了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用.
通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长L=和扇形面积S扇=的计算公式,并应用这些公式解决一些题目.
三、教学重难点
重点:n°的圆心角所对的弧长L=,扇形面积S扇=及其它们的应用.
难点:两个公式的应用.
四、教学过程
(一)复习引入
(老师口问,学生口答)请同学们回答下列问题.
1.圆的周长公式是什么?
2.圆的面积公式是什么?
3.什么叫弧长?
老师点评:(1)圆的周长C=2R
(2)圆的面积S图=R2
(3)弧长就是圆的一部分.
(二)探索新知
(小黑板)请同学们独立完成下题:设圆的半径为R,则:
1.圆的周长可以看作______度的圆心角所对的弧.
2.1°的圆心角所对的弧长是_______.
3.2°的圆心角所对的弧长是_______.
4.4°的圆心角所对的弧长是_______.
……
5.n°的圆心角所对的弧长是_______.
(老师点评)根据同学们的解题过程,我们可得到:
n°的圆心角所对的弧长为
例1制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算如图所示的管道的展直长度,即的长(结果精确到0.1mm)
分析:要求的弧长,圆心角知,半径知,只要代入弧长公式即可.
解:R=40mm,n=110
∴的长==≈76.8(mm)
因此,管道的展直长度约为76.8mm.
问题:(学生分组讨论)在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:
(1)这头牛吃草的最大活动区域有多大?
(2)如果这头牛只能绕柱子转过n°角,那么它的最大活动区域有多大?
学生提问后,老师点评:(1)这头牛吃草的最大活动区域是一个以A(柱子)为圆心,5m为半径的圆的面积.
(2)如果这头牛只能绕柱子转过n°角,那么它的最大活动区域应该是n°圆心角的两个半径的n°圆心角所对的弧所围成的圆的一部分的图形,如图:
像这样,由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
(小黑板),请同学们结合圆心面积S=R2的公式,独立完成下题:
1.该图的面积可以看作是_______度的圆心角所对的扇形的面积.
2.设圆的半径为R,1°的圆心角所对的扇形面积S扇形=_______.
3.设圆的半径为R,2°的圆心角所对的扇形面积S扇形=_______.
4.设圆的半径为R,5°的圆心角所对的扇形面积S扇形=_______.
……
5.设圆半径为R,n°的圆心角所对的扇形面积S扇形=_______.
老师检察学生练习情况并点评
1.360 2.S扇形=R2 3.S扇形=R2 4.S扇形= 5.S扇形=
因此:在半径为R的圆中,圆心角n°的扇形
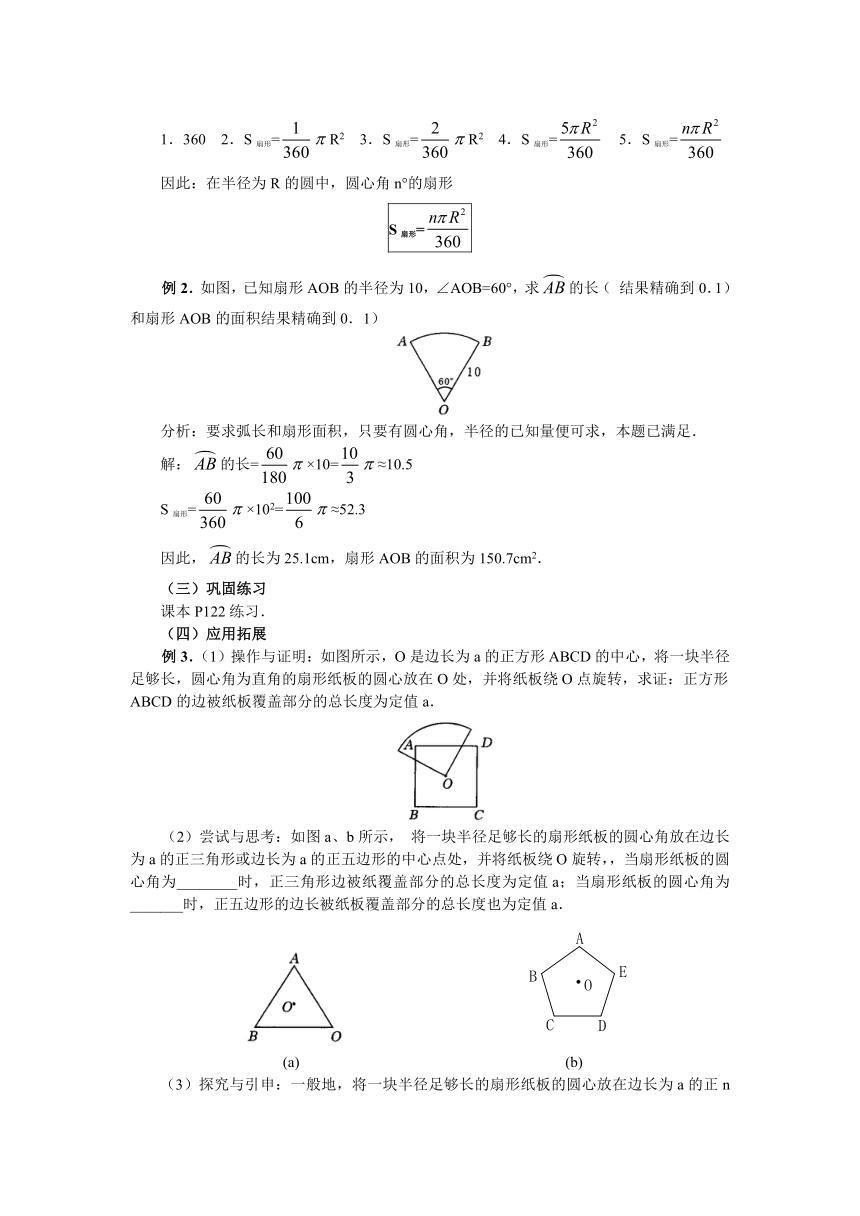
S扇形=
例2.如图,已知扇形AOB的半径为10,∠AOB=60°,求的长(结果精确到0.1)和扇形AOB的面积结果精确到0.1)
分析:要求弧长和扇形面积,只要有圆心角,半径的已知量便可求,本题已满足.
解:的长=×10=≈10.5
S扇形=×102=≈52.3
因此,的长为25.1cm,扇形AOB的面积为150.7cm2.
(三)巩固练习
课本P122练习.
(四)应用拓展
例3.(1)操作与证明:如图所示,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心角为直角的扇形纸板的圆心放在O处,并将纸板绕O点旋转,求证:正方形ABCD的边被纸板覆盖部分的总长度为定值a.
(2)尝试与思考:如图a、b所示,将一块半径足够长的扇形纸板的圆心角放在边长为a的正三角形或边长为a的正五边形的中心点处,并将纸板绕O旋转,,当扇形纸板的圆心角为________时,正三角形边被纸覆盖部分的总长度为定值a;当扇形纸板的圆心角为_______时,正五边形的边长被纸板覆盖部分的总长度也为定值a.
(a) (b)
(3)探究与引申:一般地,将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形的中心O点处,若将纸板绕O点旋转,当扇形纸板的圆心角为_______时,正n边形的边被纸板覆盖部分的总长度为定值a,这时正n边形被纸板所覆盖部分的面积是否也为定值?若为定值,写出它与正n边形面积S之间的关系(不需证明);若不是定值,请说明理由.
解:(1)如图所示,不妨设扇形纸板的两边与正方形的边AB、AD分别交于点M、N,连结OA、OD.
∵四边形ABCD是正方形
∴OA=OD,∠AOD=90°,∠MAO=∠NDO,
又∠MON=90°,∠AOM=∠DON
∴△AMO≌△DNO
∴AM=DN
∴AM+AN=DN+AN=AD=a
特别地,当点M与点A(点B)重合时,点N必与点D(点A)重合,此时AM+AN仍为定值a.
故总有正方形的边被纸板覆盖部分的总长度为定值a.
(2)120°;70°
(3);正n边形被纸板覆盖部分的面积是定值,这个定值是.
(五)归纳小结(学生小结,老师点评)
本节课应掌握:
1.n°的圆心角所对的弧长L=
2.扇形的概念.
3.圆心角为n°的扇形面积是S扇形=
4.运用以上内容,解决具体问题.
(六)布置作业
1.教材P124 复习巩固1、2、3 P125 综合运用5、6、7.
2.选用课时作业设计.
第一课时作业设计
选择题
1.已知扇形的圆心角为120°,半径为6,则扇形的弧长是( ).
A.3 B.4 C.5 D.6
2.如图1所示,把边长为2的正方形ABCD的一边放在定直线L上,按顺时针方向绕点D旋转到如图的位置,则点B运动到点B′所经过的路线长度为( )
A.1 B. C. D.
(1) (2) (3)
3.如图2所示,实数部分是半径为9m的两条等弧组成的游泳池,若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长为( )
A.12m B.18m C.20m D.24m
二、填空题
1.如果一条弧长等于R,它的半径是R,那么这条弧所对的圆心角度数为______, 当圆心角增加30°时,这条弧长增加________.
2.如图3所示,OA=30B,则的长是的长的_____倍.
三、综合提高题
1.已知如图所示,所在圆的半径为R,的长为R,⊙O′和OA、OB分别相切于点C、E,且与⊙O内切于点D,求⊙O′的周长.
2.如图,若⊙O的周长为20cm,⊙A、⊙B的周长都是4cm,⊙A在⊙O内沿⊙O滚动,⊙B在⊙O外沿⊙O滚动,⊙B转动6周回到原来的位置,而⊙A只需转动4周即可,你能说出其中的道理吗?
3.如图所示,在计算机白色屏幕上,有一矩形着色画刷ABCD,AB=1,AD=,将画刷以B为中心,按顺时针转动A′B′C′D′位置(A′点转在对角线BD上),求屏幕被着色的面积.
答案:
一、1.B 2.D 3.D
二、1.45° R 2.3
三、1.连结OD、O′C,则O′在OD上
由=R,解得:∠AOB=60°,
由Rt△OO′C解得⊙O′的半径r=R,所以⊙O′的周长为2r=R.
2.⊙O、⊙A、⊙B的周长分别为20cm,4cm,4cm,
可求出它的半径分别为10cm、2cm、2cm,
所以OA=8cm,OB=12cm,
因为圆滚动的距离实际等于其圆心经过的距离,
所以⊙A滚动回原位置经过距离为2×8=16=4×4,
而⊙B滚动回原位置经过距离为2×12=24=4×6.
因此,与原题意相符.
3.设屏幕被着色面积为S,
则S=S△ABD+S扇形BDD`+S△BC`D`=S矩形ABCD+S扇形BDD`,
连结BD′,
在Rt△A′BD′中,A′B=1,A′D′=AD=,
∴BD′=BD=2,∠DBD′=60°,
∴S=·22+1·=+.
五、板书设计
六、教学反思
教学过程中,强调学生应熟记相关公式并灵活运用,特别是求阴影部分的面积时,要灵活割补法、转换法等.
一、教学内容
1.n°的圆心角所对的弧长L=
2.扇形的概念;
3.圆心角为n°的扇形面积是S扇形=;
4.应用以上内容解决一些具体题目.
二、教学目标
了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用.
通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长L=和扇形面积S扇=的计算公式,并应用这些公式解决一些题目.
三、教学重难点
重点:n°的圆心角所对的弧长L=,扇形面积S扇=及其它们的应用.
难点:两个公式的应用.
四、教学过程
(一)复习引入
(老师口问,学生口答)请同学们回答下列问题.
1.圆的周长公式是什么?
2.圆的面积公式是什么?
3.什么叫弧长?
老师点评:(1)圆的周长C=2R
(2)圆的面积S图=R2
(3)弧长就是圆的一部分.
(二)探索新知
(小黑板)请同学们独立完成下题:设圆的半径为R,则:
1.圆的周长可以看作______度的圆心角所对的弧.
2.1°的圆心角所对的弧长是_______.
3.2°的圆心角所对的弧长是_______.
4.4°的圆心角所对的弧长是_______.
……
5.n°的圆心角所对的弧长是_______.
(老师点评)根据同学们的解题过程,我们可得到:
n°的圆心角所对的弧长为
例1制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算如图所示的管道的展直长度,即的长(结果精确到0.1mm)
分析:要求的弧长,圆心角知,半径知,只要代入弧长公式即可.
解:R=40mm,n=110
∴的长==≈76.8(mm)
因此,管道的展直长度约为76.8mm.
问题:(学生分组讨论)在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:
(1)这头牛吃草的最大活动区域有多大?
(2)如果这头牛只能绕柱子转过n°角,那么它的最大活动区域有多大?
学生提问后,老师点评:(1)这头牛吃草的最大活动区域是一个以A(柱子)为圆心,5m为半径的圆的面积.
(2)如果这头牛只能绕柱子转过n°角,那么它的最大活动区域应该是n°圆心角的两个半径的n°圆心角所对的弧所围成的圆的一部分的图形,如图:
像这样,由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
(小黑板),请同学们结合圆心面积S=R2的公式,独立完成下题:
1.该图的面积可以看作是_______度的圆心角所对的扇形的面积.
2.设圆的半径为R,1°的圆心角所对的扇形面积S扇形=_______.
3.设圆的半径为R,2°的圆心角所对的扇形面积S扇形=_______.
4.设圆的半径为R,5°的圆心角所对的扇形面积S扇形=_______.
……
5.设圆半径为R,n°的圆心角所对的扇形面积S扇形=_______.
老师检察学生练习情况并点评
1.360 2.S扇形=R2 3.S扇形=R2 4.S扇形= 5.S扇形=
因此:在半径为R的圆中,圆心角n°的扇形
S扇形=
例2.如图,已知扇形AOB的半径为10,∠AOB=60°,求的长(结果精确到0.1)和扇形AOB的面积结果精确到0.1)
分析:要求弧长和扇形面积,只要有圆心角,半径的已知量便可求,本题已满足.
解:的长=×10=≈10.5
S扇形=×102=≈52.3
因此,的长为25.1cm,扇形AOB的面积为150.7cm2.
(三)巩固练习
课本P122练习.
(四)应用拓展
例3.(1)操作与证明:如图所示,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心角为直角的扇形纸板的圆心放在O处,并将纸板绕O点旋转,求证:正方形ABCD的边被纸板覆盖部分的总长度为定值a.
(2)尝试与思考:如图a、b所示,将一块半径足够长的扇形纸板的圆心角放在边长为a的正三角形或边长为a的正五边形的中心点处,并将纸板绕O旋转,,当扇形纸板的圆心角为________时,正三角形边被纸覆盖部分的总长度为定值a;当扇形纸板的圆心角为_______时,正五边形的边长被纸板覆盖部分的总长度也为定值a.
(a) (b)
(3)探究与引申:一般地,将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形的中心O点处,若将纸板绕O点旋转,当扇形纸板的圆心角为_______时,正n边形的边被纸板覆盖部分的总长度为定值a,这时正n边形被纸板所覆盖部分的面积是否也为定值?若为定值,写出它与正n边形面积S之间的关系(不需证明);若不是定值,请说明理由.
解:(1)如图所示,不妨设扇形纸板的两边与正方形的边AB、AD分别交于点M、N,连结OA、OD.
∵四边形ABCD是正方形
∴OA=OD,∠AOD=90°,∠MAO=∠NDO,
又∠MON=90°,∠AOM=∠DON
∴△AMO≌△DNO
∴AM=DN
∴AM+AN=DN+AN=AD=a
特别地,当点M与点A(点B)重合时,点N必与点D(点A)重合,此时AM+AN仍为定值a.
故总有正方形的边被纸板覆盖部分的总长度为定值a.
(2)120°;70°
(3);正n边形被纸板覆盖部分的面积是定值,这个定值是.
(五)归纳小结(学生小结,老师点评)
本节课应掌握:
1.n°的圆心角所对的弧长L=
2.扇形的概念.
3.圆心角为n°的扇形面积是S扇形=
4.运用以上内容,解决具体问题.
(六)布置作业
1.教材P124 复习巩固1、2、3 P125 综合运用5、6、7.
2.选用课时作业设计.
第一课时作业设计
选择题
1.已知扇形的圆心角为120°,半径为6,则扇形的弧长是( ).
A.3 B.4 C.5 D.6
2.如图1所示,把边长为2的正方形ABCD的一边放在定直线L上,按顺时针方向绕点D旋转到如图的位置,则点B运动到点B′所经过的路线长度为( )
A.1 B. C. D.
(1) (2) (3)
3.如图2所示,实数部分是半径为9m的两条等弧组成的游泳池,若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长为( )
A.12m B.18m C.20m D.24m
二、填空题
1.如果一条弧长等于R,它的半径是R,那么这条弧所对的圆心角度数为______, 当圆心角增加30°时,这条弧长增加________.
2.如图3所示,OA=30B,则的长是的长的_____倍.
三、综合提高题
1.已知如图所示,所在圆的半径为R,的长为R,⊙O′和OA、OB分别相切于点C、E,且与⊙O内切于点D,求⊙O′的周长.
2.如图,若⊙O的周长为20cm,⊙A、⊙B的周长都是4cm,⊙A在⊙O内沿⊙O滚动,⊙B在⊙O外沿⊙O滚动,⊙B转动6周回到原来的位置,而⊙A只需转动4周即可,你能说出其中的道理吗?
3.如图所示,在计算机白色屏幕上,有一矩形着色画刷ABCD,AB=1,AD=,将画刷以B为中心,按顺时针转动A′B′C′D′位置(A′点转在对角线BD上),求屏幕被着色的面积.
答案:
一、1.B 2.D 3.D
二、1.45° R 2.3
三、1.连结OD、O′C,则O′在OD上
由=R,解得:∠AOB=60°,
由Rt△OO′C解得⊙O′的半径r=R,所以⊙O′的周长为2r=R.
2.⊙O、⊙A、⊙B的周长分别为20cm,4cm,4cm,
可求出它的半径分别为10cm、2cm、2cm,
所以OA=8cm,OB=12cm,
因为圆滚动的距离实际等于其圆心经过的距离,
所以⊙A滚动回原位置经过距离为2×8=16=4×4,
而⊙B滚动回原位置经过距离为2×12=24=4×6.
因此,与原题意相符.
3.设屏幕被着色面积为S,
则S=S△ABD+S扇形BDD`+S△BC`D`=S矩形ABCD+S扇形BDD`,
连结BD′,
在Rt△A′BD′中,A′B=1,A′D′=AD=,
∴BD′=BD=2,∠DBD′=60°,
∴S=·22+1·=+.
五、板书设计
六、教学反思
教学过程中,强调学生应熟记相关公式并灵活运用,特别是求阴影部分的面积时,要灵活割补法、转换法等.
同课章节目录
