人教版五年级上册数学四边形的面积(教案)
文档属性
| 名称 | 人教版五年级上册数学四边形的面积(教案) |  | |
| 格式 | doc | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 12:26:14 | ||
图片预览

文档简介
四边形的面积拓展课
一、教学目标
在方格纸上,能够算出长方形、正方形和特殊的梯形和平行四边形的面积。
在灵活运用割补法探索图形的面积时,感悟当平行四边形的底和高确定后,这个图形的面积也相应的确定。
初步感悟面积的大小是由基本单位累加的过程。
教学重难点
重点:灵活运用割补法求特殊图形的面积
难点:感悟平行四边形的底和高确定后,这个图形的面积也相应的确定。
教学准备
多媒体课件
教学流程
开门见山,导入新课
师:同学们,今天这节课,我们一起研究四边形的面积。(板书课题:四边形的面积)
师:四边形的种类有很多,从谁开始研究呢?引导:由特殊四边形到一般四边形。
【设计意图】开门见山,直入主题,简单明了。
层层递进,感悟面积本质
1.布置任务
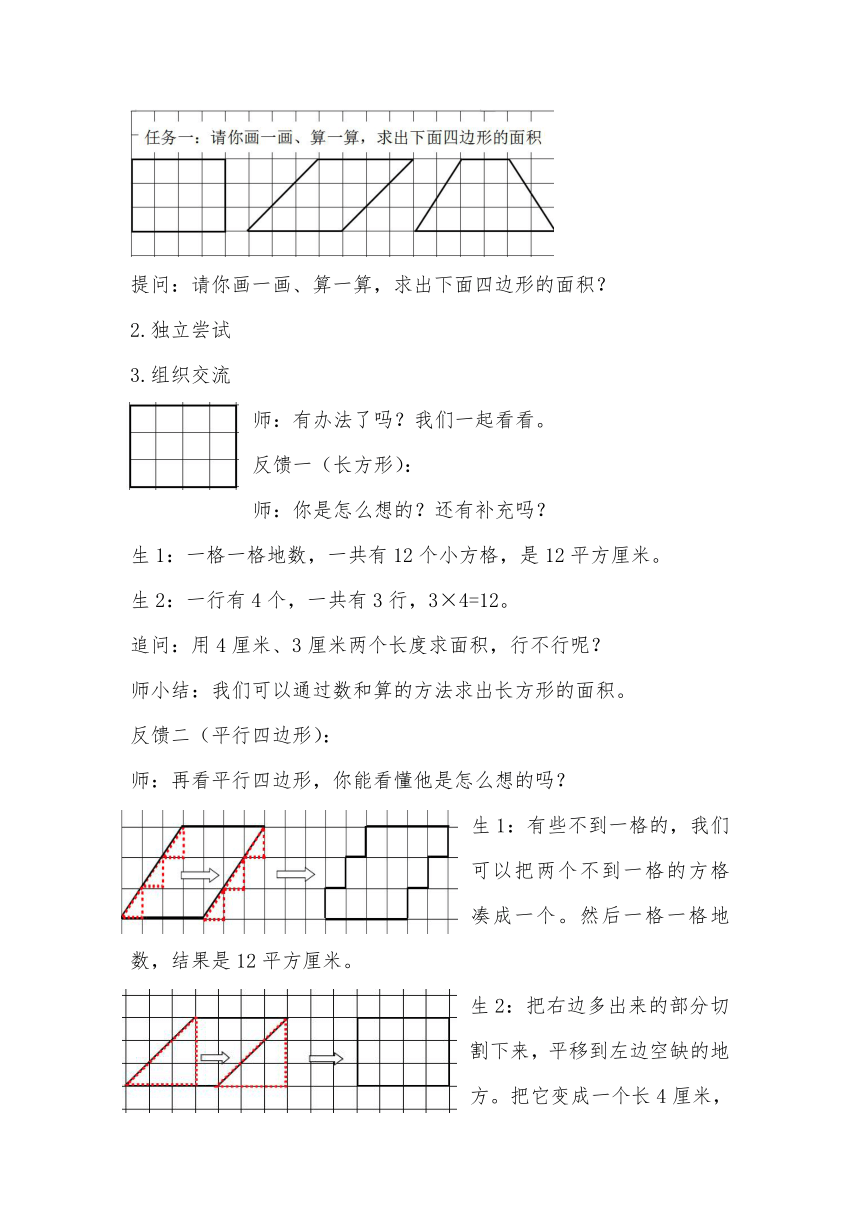
提问:请你画一画、算一算,求出下面四边形的面积?
2.独立尝试
3.组织交流
师:有办法了吗?我们一起看看。
反馈一(长方形):
师:你是怎么想的?还有补充吗?
生1:一格一格地数,一共有12个小方格,是12平方厘米。
生2:一行有4个,一共有3行,3×4=12。
追问:用4厘米、3厘米两个长度求面积,行不行呢?
师小结:我们可以通过数和算的方法求出长方形的面积。
反馈二(平行四边形):
师:再看平行四边形,你能看懂他是怎么想的吗?
生1:有些不到一格的,我们可以把两个不到一格的方格凑成一个。然后一格一格地数,结果是12平方厘米。
生2:把右边多出来的部分切割下来,平移到左边空缺的地方。把它变成一个长4厘米,宽3厘米的长方形。再算面积。
提问:这样割补,面积会变吗?
师生小结:不会变(直观感受)。很巧妙地把右边凸出来的右边的部分平移到左边,将平行四边形转化为长方形。这样算面积更快!
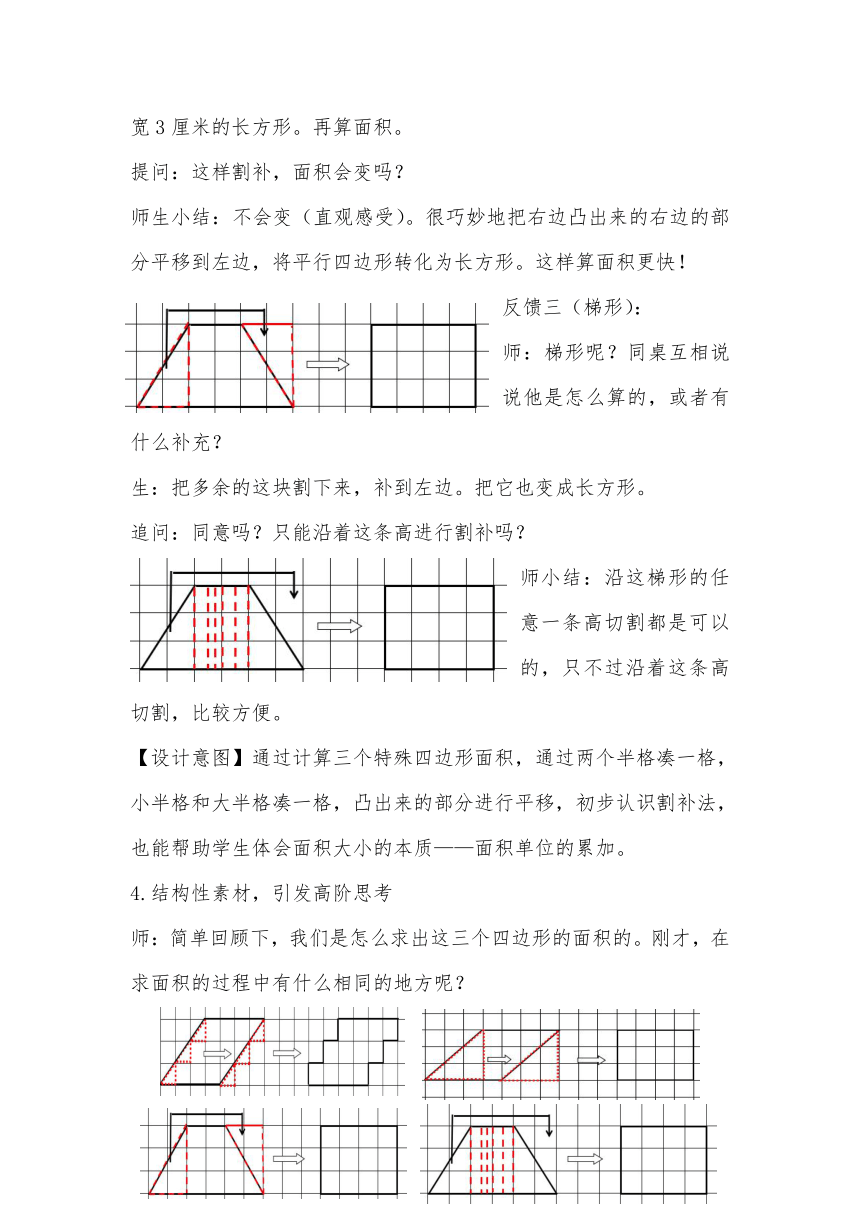
反馈三(梯形):
师:梯形呢?同桌互相说说他是怎么算的,或者有什么补充?
生:把多余的这块割下来,补到左边。把它也变成长方形。
追问:同意吗?只能沿着这条高进行割补吗?
师小结:沿这梯形的任意一条高切割都是可以的,只不过沿着这条高切割,比较方便。
【设计意图】通过计算三个特殊四边形面积,通过两个半格凑一格,小半格和大半格凑一格,凸出来的部分进行平移,初步认识割补法,也能帮助学生体会面积大小的本质——面积单位的累加。
4.结构性素材,引发高阶思考
师:简单回顾下,我们是怎么求出这三个四边形的面积的。刚才,在求面积的过程中有什么相同的地方呢?
生1:面积是相同的。
生2:都是通过割补法,把平行四边形和梯形转化为长方形,这样算得快。
师小结:求面积时,我们可以通过割补法,把不规则图形的面积转化为规则图形面积,这样的方法,算的更快一些。
提问:诶,挺奇怪的,形状不同,为什么它们面积算出来是相等的?
生1:这些图形里面都有12个1平方厘米的小正方形。
生2:它们都能转为长4厘米,宽3厘米的长方形。面积肯定是一样的。
生3:它们的底和高是一样的,所以面积一定相等。
师小结:不错!想法是一个比一个厉害!这种感觉到底对不对呢?我们进一步地来感受下面积的大小究竟跟图形的什么有关系?
【设计意图】割补法计算面积不单单是简单地操作,更要关注在操作中,发现素材中的联系性,引发学生高阶思考:形状不一样,为什么它们的面积相同?图形的面积大小和图形的什么有关系呢?
(三)前置作业,沟通联系
师:上一节课,我们完成了一份作业:画底是4厘米,高是4厘米的平行四边形和画上底是2厘米,下底是6厘米,高是4厘米的梯形。
1.布置任务
(1)两组材料,选择其中一种进行研究。
(2)算一算这组材料中的面积,想一想这个图形面积的大小可能和这个图形的什么有关系?
2.独立尝试。
3.组织交流
(1)展示作业
展示1:
生:底是4厘米,高是4厘米的平行四边形,形状有很多种,我们组算出来的面积都是一样的,都是16平方厘米。由此,我们猜想,平行四边形的底和高确定了,它的面积也就确定了。
追问:通过这样一组数据和你们自己算出来的结果,同意这种想法吗?指名两生回答。
展示2:
生:梯形有可能麻烦些,上底是2厘米,下底是6厘米的梯形,高是4厘米的梯形,形状也有很多种,我们组算出出来的面积也是一样的,都是16平方厘米。由此,我们猜想,梯形的上底、下底和高确定了,它的面积也就确定了。
师小结:真会思考,其实,就像你们刚才说的那样,平行四边形和梯形的底和高确定了,相应图形的面积也就确定了。
【设计意图】通过学习材料的前后顺序,增强学生学习的连续性。内在问题驱动学生自主探究,感悟平行四边形、梯形的底和高确定后,面积也就相应的确定了,
4.思考反思,留有悬念
师:有没有发现又有一个好巧的事,底是4厘米,高是4厘米的这类平行四边形,上底是2厘米,下底是6厘米的这类梯形,高是4厘米的梯形,这两类四边形面积算出来都是16平方厘米。这里面又藏着什么玄机呢?
生1:通过割补法,都能把它们转化为长是4厘米,宽是4厘米的正方形。
生2:高是一样的,其实底也是一样的,2+6=8厘米,8÷2=4厘米,也就是平行四边形的底。
师小结:你们真会观察和思考。究竟是怎么回事呢?五年级,我们再进一步学习梯形、三角形、平行四边形的面积。事实上,它们面积计算,在一定角度上看,都是一样的。感兴趣的孩子,下课后,通过你们的方式进一步深度学习。
【设计意图】同样这组平行四边形和梯形也为结构性材料,通过计算,了解到等底等高的平行四边形和梯形面积相等。进一步引发思考,两者有什么联系,为后续五年级面积的学习奠定基础。
全课总结
师:通过今天这节课的学习,你有什么收获?
一、教学目标
在方格纸上,能够算出长方形、正方形和特殊的梯形和平行四边形的面积。
在灵活运用割补法探索图形的面积时,感悟当平行四边形的底和高确定后,这个图形的面积也相应的确定。
初步感悟面积的大小是由基本单位累加的过程。
教学重难点
重点:灵活运用割补法求特殊图形的面积
难点:感悟平行四边形的底和高确定后,这个图形的面积也相应的确定。
教学准备
多媒体课件
教学流程
开门见山,导入新课
师:同学们,今天这节课,我们一起研究四边形的面积。(板书课题:四边形的面积)
师:四边形的种类有很多,从谁开始研究呢?引导:由特殊四边形到一般四边形。
【设计意图】开门见山,直入主题,简单明了。
层层递进,感悟面积本质
1.布置任务
提问:请你画一画、算一算,求出下面四边形的面积?
2.独立尝试
3.组织交流
师:有办法了吗?我们一起看看。
反馈一(长方形):
师:你是怎么想的?还有补充吗?
生1:一格一格地数,一共有12个小方格,是12平方厘米。
生2:一行有4个,一共有3行,3×4=12。
追问:用4厘米、3厘米两个长度求面积,行不行呢?
师小结:我们可以通过数和算的方法求出长方形的面积。
反馈二(平行四边形):
师:再看平行四边形,你能看懂他是怎么想的吗?
生1:有些不到一格的,我们可以把两个不到一格的方格凑成一个。然后一格一格地数,结果是12平方厘米。
生2:把右边多出来的部分切割下来,平移到左边空缺的地方。把它变成一个长4厘米,宽3厘米的长方形。再算面积。
提问:这样割补,面积会变吗?
师生小结:不会变(直观感受)。很巧妙地把右边凸出来的右边的部分平移到左边,将平行四边形转化为长方形。这样算面积更快!
反馈三(梯形):
师:梯形呢?同桌互相说说他是怎么算的,或者有什么补充?
生:把多余的这块割下来,补到左边。把它也变成长方形。
追问:同意吗?只能沿着这条高进行割补吗?
师小结:沿这梯形的任意一条高切割都是可以的,只不过沿着这条高切割,比较方便。
【设计意图】通过计算三个特殊四边形面积,通过两个半格凑一格,小半格和大半格凑一格,凸出来的部分进行平移,初步认识割补法,也能帮助学生体会面积大小的本质——面积单位的累加。
4.结构性素材,引发高阶思考
师:简单回顾下,我们是怎么求出这三个四边形的面积的。刚才,在求面积的过程中有什么相同的地方呢?
生1:面积是相同的。
生2:都是通过割补法,把平行四边形和梯形转化为长方形,这样算得快。
师小结:求面积时,我们可以通过割补法,把不规则图形的面积转化为规则图形面积,这样的方法,算的更快一些。
提问:诶,挺奇怪的,形状不同,为什么它们面积算出来是相等的?
生1:这些图形里面都有12个1平方厘米的小正方形。
生2:它们都能转为长4厘米,宽3厘米的长方形。面积肯定是一样的。
生3:它们的底和高是一样的,所以面积一定相等。
师小结:不错!想法是一个比一个厉害!这种感觉到底对不对呢?我们进一步地来感受下面积的大小究竟跟图形的什么有关系?
【设计意图】割补法计算面积不单单是简单地操作,更要关注在操作中,发现素材中的联系性,引发学生高阶思考:形状不一样,为什么它们的面积相同?图形的面积大小和图形的什么有关系呢?
(三)前置作业,沟通联系
师:上一节课,我们完成了一份作业:画底是4厘米,高是4厘米的平行四边形和画上底是2厘米,下底是6厘米,高是4厘米的梯形。
1.布置任务
(1)两组材料,选择其中一种进行研究。
(2)算一算这组材料中的面积,想一想这个图形面积的大小可能和这个图形的什么有关系?
2.独立尝试。
3.组织交流
(1)展示作业
展示1:
生:底是4厘米,高是4厘米的平行四边形,形状有很多种,我们组算出来的面积都是一样的,都是16平方厘米。由此,我们猜想,平行四边形的底和高确定了,它的面积也就确定了。
追问:通过这样一组数据和你们自己算出来的结果,同意这种想法吗?指名两生回答。
展示2:
生:梯形有可能麻烦些,上底是2厘米,下底是6厘米的梯形,高是4厘米的梯形,形状也有很多种,我们组算出出来的面积也是一样的,都是16平方厘米。由此,我们猜想,梯形的上底、下底和高确定了,它的面积也就确定了。
师小结:真会思考,其实,就像你们刚才说的那样,平行四边形和梯形的底和高确定了,相应图形的面积也就确定了。
【设计意图】通过学习材料的前后顺序,增强学生学习的连续性。内在问题驱动学生自主探究,感悟平行四边形、梯形的底和高确定后,面积也就相应的确定了,
4.思考反思,留有悬念
师:有没有发现又有一个好巧的事,底是4厘米,高是4厘米的这类平行四边形,上底是2厘米,下底是6厘米的这类梯形,高是4厘米的梯形,这两类四边形面积算出来都是16平方厘米。这里面又藏着什么玄机呢?
生1:通过割补法,都能把它们转化为长是4厘米,宽是4厘米的正方形。
生2:高是一样的,其实底也是一样的,2+6=8厘米,8÷2=4厘米,也就是平行四边形的底。
师小结:你们真会观察和思考。究竟是怎么回事呢?五年级,我们再进一步学习梯形、三角形、平行四边形的面积。事实上,它们面积计算,在一定角度上看,都是一样的。感兴趣的孩子,下课后,通过你们的方式进一步深度学习。
【设计意图】同样这组平行四边形和梯形也为结构性材料,通过计算,了解到等底等高的平行四边形和梯形面积相等。进一步引发思考,两者有什么联系,为后续五年级面积的学习奠定基础。
全课总结
师:通过今天这节课的学习,你有什么收获?
