新课标北师大版六上6.1《生活中的比》课件(32张PPT)
文档属性
| 名称 | 新课标北师大版六上6.1《生活中的比》课件(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 09:32:16 | ||
图片预览






文档简介
(共32张PPT)
生活中的比
北师大版六年级上册
教学目标
1.学习目标描述:经历从具体情境中抽象出比的过程,理解比的意义,能正确读写比,体会比与除法的关系。
2.学习内容分析:教材通过密切联系学生已有的生活经验和学习经验,提供了“图形放大缩小”“速度”“水果价格”等情境,引发学生的讨论和思考,使学生经历从具体情境中抽象出比的意义的过程,理解比的意义,从而让学生体会引入比的必要性,感受比在生活中的广泛存在;也为 “比的应用 ”“比例的相关知识”等后续学习打下铺垫。
教学目标
3.学科核心素养分析:体会引入比的必要性,能利用比的知识解释一些简单的生活问题, 感受比在生活中的广泛存在,激发学生学习数学的兴趣,感受学习数学的价值,增强学生的应用意识。
新知导入
1.用分数表示下面除法算式的结果。
3÷4=( ) 6÷5=( ) 8÷13=( )
3
4
6
5
8
13
分数与除法的联系和区别是什么?
分数
除法
联 系 区 别
分子
分数线
分母
被除数
除号
除数
是一种运算
是一种运算
新知导入
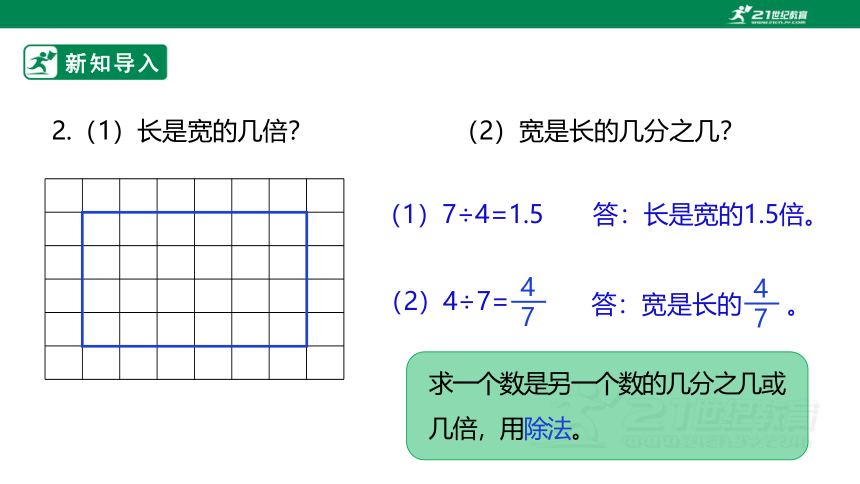
2.(1)长是宽的几倍? (2)宽是长的几分之几?
(1)7÷4=1.5
答:长是宽的1.5倍。
(2)4÷7=
4
7
答:宽是长的 。
4
7
求一个数是另一个数的几分之几或几倍,用除法。
新知导入
比较两个数量之间的倍数关系用除法
在日常生活和工农业生产中,常常需要对两个数量进行比较,比较的方法我们已经学过两种。
比较两个数量之间相差关系用减法
新知讲解
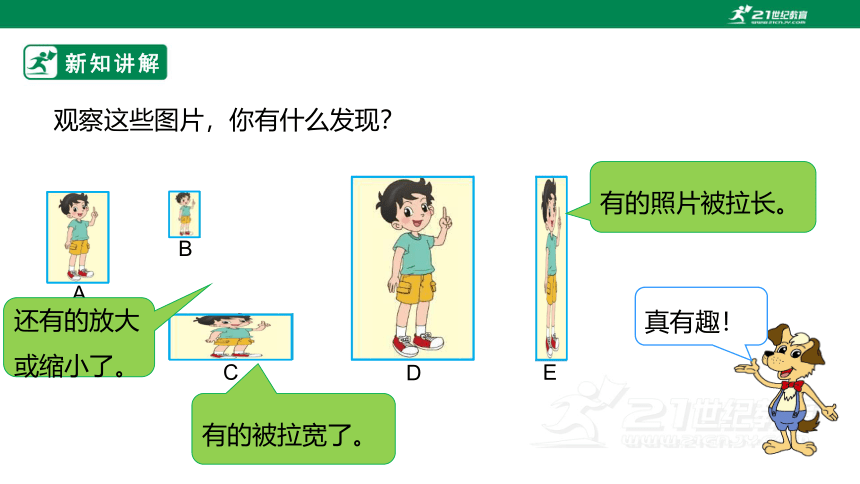
观察这些图片,你有什么发现?
A
B
C
D
E
有的照片被拉长。
有的被拉宽了。
还有的放大或缩小了。
真有趣!
新知讲解
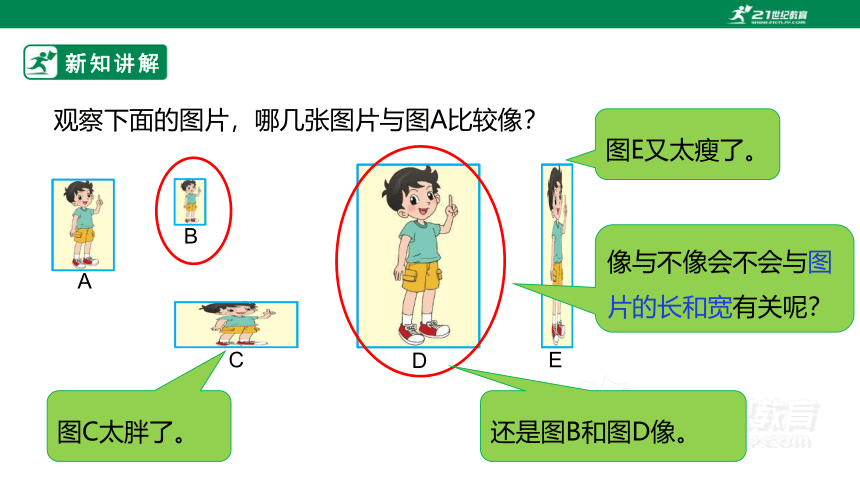
观察下面的图片,哪几张图片与图A比较像?
A
B
C
D
E
图C太胖了。
图E又太瘦了。
还是图B和图D像。
像与不像会不会与图片的长和宽有关呢?
新知讲解
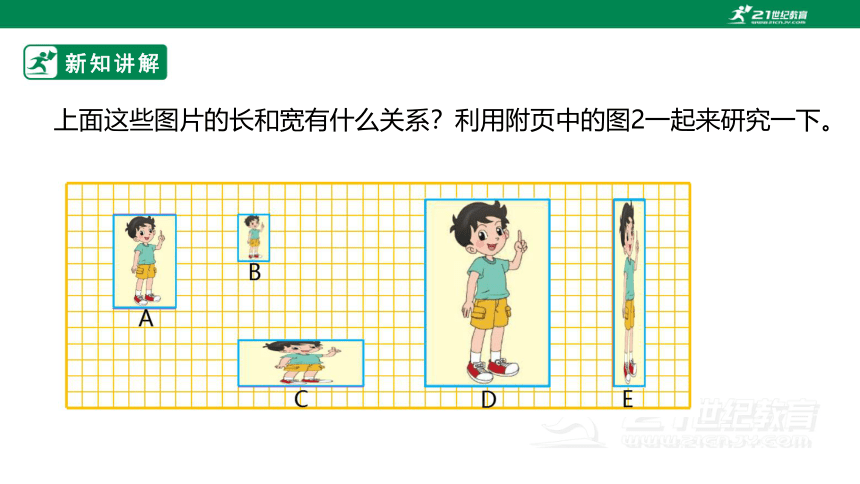
上面这些图片的长和宽有什么关系?利用附页中的图2一起来研究一下。
新知讲解
小组合作交流:
1. 请先标出长和宽,一个方格的边长为 1。
2.B、D的长和宽分别与A的长和宽有什么关系?
新知讲解
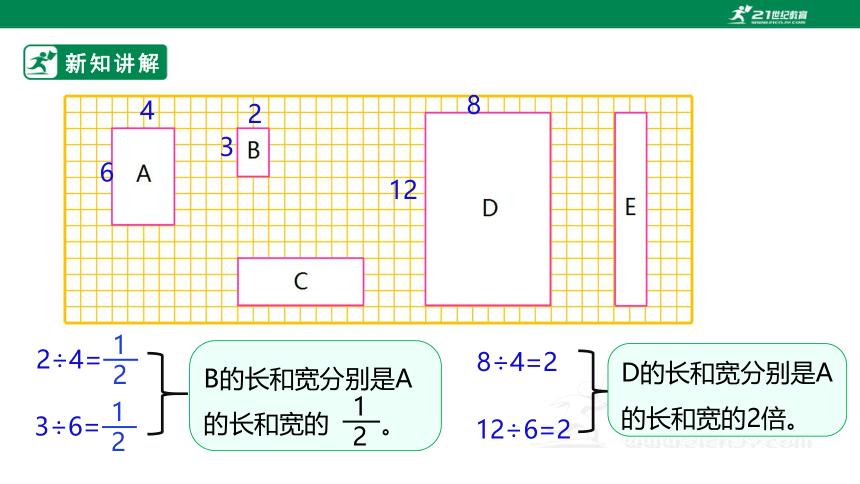
6
4
3
2
12
8
2÷4=
1
2
3÷6=
1
2
B的长和宽分别是A的长和宽的 。
1
2
8÷4=2
12÷6=2
D的长和宽分别是A的长和宽的2倍。
新知讲解
上面这些图片的长和宽有什么关系?利用附页中的图2一起来研究一下。
6÷4=1.5
3÷2=1.5
12÷8=1.5
A、B、D的长都是宽的1.5倍。
4÷6=
2
3
2÷3=
2
3
8÷12=
2
3
A、B、D的宽都是长的 。
2
3
新知讲解
现在你知道 ABD 比较像的道理了吗? 谁来说一说。
B、D的长与宽与A的长和宽扩大或缩小的倍数相同,所以B、D与A比较像。
A、B、D的长都是宽的1. 5倍,宽都是长的 ,所以它们比较像。
2
3
新知讲解
自学提示:
自学教材69页“认一认”部分,并用笔勾出认为关键的词语或句子。
新知讲解
两个数相除又叫做两个数的比。
如,6÷4可以写作6 : 4,读作6比4。
…
比号
新知讲解
你知道吗?
十七世纪,数学家莱布尼兹认为,两个量的比,包含有除的意思,但又不能占用÷,于是他把除号中的小横线去掉,于是“ : ”就成了比号。
新知讲解
6 : 4
=6 ÷ 4
=1.5
…
前
项
…
后
项
…
比
值
比的前项除以后项所得的商叫比值,比值常用分数表示,也可用小数、整数表示。
比也可以写成分数形式,如 ,仍读作6比4。
6
4
6
4
=
新知讲解
你能联系实际说说生活中有哪些比吗?
我们班男生与女生的人数比是26:23。
教室里桌子与椅子的数量比是49:49。
像这种相比的两个量是同类的量,叫做同类量比。
新知讲解
说说下面各比的含义。
1份甘蔗汁2份水,
2份甘蔗汁4份水,
……
树高是影子的2倍,影长是树高的 。
新知讲解
填一填,说一说。
路程 时间 路程与 时间的比 速度
马拉松选手 40km 2时
骑车人 45km 3时
(1)谁快?
40:2
45:3
20千米/时
15千米/时
速度又可以说成路程和时间的比。
新知讲解
填一填,说一说。
品种 总价 数量 总价与 数量的比 单价
A 9元 2kg
B 15元 3kg
C 12元 3kg
(2)哪种苹果最便宜?
9:2
15:3
4.5元/kg
5元/kg
苹果的单价可以说成总价与数量的比。
12:3
4元/kg
新知讲解
生活中我们不仅需要同类量比, 还需要不同类量比。
新知讲解
想一想,比与分数、除法有什么关系?与同伴交流。
6 : 4
6
4
=
=6 ÷ 4
=1.5
联 系 区 别
除法
分数
比
被除数
除数
÷(除号)
商
分子
分母
分数值
前项
后项
:(比号)
比值
(分数线)
不能为0。
课堂练习
1.填一填。
甲数是5,乙数是4。
(1)甲数与乙数的比是( ),乙数与甲数的比是( )。
(2)甲数与两数的和的比是( ),乙数与两数的和的比是( )。
(3)甲数与两数的差的比是( ),乙数与两数的差的比是( )。
5:4
4:5
5:9
4:9
5:1
4:1
课堂练习
2.求出比值。
4:5= 34:12= 5:9=
2.4:0.4= 35:7= : =
4÷5
4
5
=
34÷12
=
17
6
5÷9
=
5
9
2.4÷0.4
=6
35÷7
=5
1
2
1
4
1
2
÷
1
4
=2
课堂练习
3.如图,两个正方形的边长之比是多少?周长之比是多少?面积之比是多少?你能得出什么结论?
5cm 3cm
(1)边长比:5:3
(2)周长比:(4×5):(4×3)=5:3
(3)面积比:(5×5):(3×3)=25:9
(4)结论:两个正方形的周长之比等于边长之比;面积之比等于边长的比平方。
课堂练习
4.拓展应用:中国著名乒乓球运动员在一次比赛中以4:0的好成绩战胜对方。这里的4:0是我们今天所学习的比吗?为什么?
4 : 0 不是数学中的“比” 。因为它只表示两个数量之间的相差关系,不表示两数的相除关系。体育比赛中的比,只是借用了数学中“比”的表示形式,其本质意义是表示双方的得分多少,所以它的前后两个数都可以是 0。体育中的“比” 与数学中的“比” 意义不同。
课堂总结
通过今天的学习,你有哪些收获?
我认识了比,知道了比各部分的名称。
我还知道了比、分数、除法之间的联系和区别。
板书设计
生活中的比
两个数相除又叫做两个数的比。
6 : 4
6
4
=
=6 ÷ 4
=1.5
…
前
项
…
后
项
…
比
值
读作:六比四
…
比
号
作业布置
完成课本“练一练”第1~4题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
生活中的比
北师大版六年级上册
教学目标
1.学习目标描述:经历从具体情境中抽象出比的过程,理解比的意义,能正确读写比,体会比与除法的关系。
2.学习内容分析:教材通过密切联系学生已有的生活经验和学习经验,提供了“图形放大缩小”“速度”“水果价格”等情境,引发学生的讨论和思考,使学生经历从具体情境中抽象出比的意义的过程,理解比的意义,从而让学生体会引入比的必要性,感受比在生活中的广泛存在;也为 “比的应用 ”“比例的相关知识”等后续学习打下铺垫。
教学目标
3.学科核心素养分析:体会引入比的必要性,能利用比的知识解释一些简单的生活问题, 感受比在生活中的广泛存在,激发学生学习数学的兴趣,感受学习数学的价值,增强学生的应用意识。
新知导入
1.用分数表示下面除法算式的结果。
3÷4=( ) 6÷5=( ) 8÷13=( )
3
4
6
5
8
13
分数与除法的联系和区别是什么?
分数
除法
联 系 区 别
分子
分数线
分母
被除数
除号
除数
是一种运算
是一种运算
新知导入
2.(1)长是宽的几倍? (2)宽是长的几分之几?
(1)7÷4=1.5
答:长是宽的1.5倍。
(2)4÷7=
4
7
答:宽是长的 。
4
7
求一个数是另一个数的几分之几或几倍,用除法。
新知导入
比较两个数量之间的倍数关系用除法
在日常生活和工农业生产中,常常需要对两个数量进行比较,比较的方法我们已经学过两种。
比较两个数量之间相差关系用减法
新知讲解
观察这些图片,你有什么发现?
A
B
C
D
E
有的照片被拉长。
有的被拉宽了。
还有的放大或缩小了。
真有趣!
新知讲解
观察下面的图片,哪几张图片与图A比较像?
A
B
C
D
E
图C太胖了。
图E又太瘦了。
还是图B和图D像。
像与不像会不会与图片的长和宽有关呢?
新知讲解
上面这些图片的长和宽有什么关系?利用附页中的图2一起来研究一下。
新知讲解
小组合作交流:
1. 请先标出长和宽,一个方格的边长为 1。
2.B、D的长和宽分别与A的长和宽有什么关系?
新知讲解
6
4
3
2
12
8
2÷4=
1
2
3÷6=
1
2
B的长和宽分别是A的长和宽的 。
1
2
8÷4=2
12÷6=2
D的长和宽分别是A的长和宽的2倍。
新知讲解
上面这些图片的长和宽有什么关系?利用附页中的图2一起来研究一下。
6÷4=1.5
3÷2=1.5
12÷8=1.5
A、B、D的长都是宽的1.5倍。
4÷6=
2
3
2÷3=
2
3
8÷12=
2
3
A、B、D的宽都是长的 。
2
3
新知讲解
现在你知道 ABD 比较像的道理了吗? 谁来说一说。
B、D的长与宽与A的长和宽扩大或缩小的倍数相同,所以B、D与A比较像。
A、B、D的长都是宽的1. 5倍,宽都是长的 ,所以它们比较像。
2
3
新知讲解
自学提示:
自学教材69页“认一认”部分,并用笔勾出认为关键的词语或句子。
新知讲解
两个数相除又叫做两个数的比。
如,6÷4可以写作6 : 4,读作6比4。
…
比号
新知讲解
你知道吗?
十七世纪,数学家莱布尼兹认为,两个量的比,包含有除的意思,但又不能占用÷,于是他把除号中的小横线去掉,于是“ : ”就成了比号。
新知讲解
6 : 4
=6 ÷ 4
=1.5
…
前
项
…
后
项
…
比
值
比的前项除以后项所得的商叫比值,比值常用分数表示,也可用小数、整数表示。
比也可以写成分数形式,如 ,仍读作6比4。
6
4
6
4
=
新知讲解
你能联系实际说说生活中有哪些比吗?
我们班男生与女生的人数比是26:23。
教室里桌子与椅子的数量比是49:49。
像这种相比的两个量是同类的量,叫做同类量比。
新知讲解
说说下面各比的含义。
1份甘蔗汁2份水,
2份甘蔗汁4份水,
……
树高是影子的2倍,影长是树高的 。
新知讲解
填一填,说一说。
路程 时间 路程与 时间的比 速度
马拉松选手 40km 2时
骑车人 45km 3时
(1)谁快?
40:2
45:3
20千米/时
15千米/时
速度又可以说成路程和时间的比。
新知讲解
填一填,说一说。
品种 总价 数量 总价与 数量的比 单价
A 9元 2kg
B 15元 3kg
C 12元 3kg
(2)哪种苹果最便宜?
9:2
15:3
4.5元/kg
5元/kg
苹果的单价可以说成总价与数量的比。
12:3
4元/kg
新知讲解
生活中我们不仅需要同类量比, 还需要不同类量比。
新知讲解
想一想,比与分数、除法有什么关系?与同伴交流。
6 : 4
6
4
=
=6 ÷ 4
=1.5
联 系 区 别
除法
分数
比
被除数
除数
÷(除号)
商
分子
分母
分数值
前项
后项
:(比号)
比值
(分数线)
不能为0。
课堂练习
1.填一填。
甲数是5,乙数是4。
(1)甲数与乙数的比是( ),乙数与甲数的比是( )。
(2)甲数与两数的和的比是( ),乙数与两数的和的比是( )。
(3)甲数与两数的差的比是( ),乙数与两数的差的比是( )。
5:4
4:5
5:9
4:9
5:1
4:1
课堂练习
2.求出比值。
4:5= 34:12= 5:9=
2.4:0.4= 35:7= : =
4÷5
4
5
=
34÷12
=
17
6
5÷9
=
5
9
2.4÷0.4
=6
35÷7
=5
1
2
1
4
1
2
÷
1
4
=2
课堂练习
3.如图,两个正方形的边长之比是多少?周长之比是多少?面积之比是多少?你能得出什么结论?
5cm 3cm
(1)边长比:5:3
(2)周长比:(4×5):(4×3)=5:3
(3)面积比:(5×5):(3×3)=25:9
(4)结论:两个正方形的周长之比等于边长之比;面积之比等于边长的比平方。
课堂练习
4.拓展应用:中国著名乒乓球运动员在一次比赛中以4:0的好成绩战胜对方。这里的4:0是我们今天所学习的比吗?为什么?
4 : 0 不是数学中的“比” 。因为它只表示两个数量之间的相差关系,不表示两数的相除关系。体育比赛中的比,只是借用了数学中“比”的表示形式,其本质意义是表示双方的得分多少,所以它的前后两个数都可以是 0。体育中的“比” 与数学中的“比” 意义不同。
课堂总结
通过今天的学习,你有哪些收获?
我认识了比,知道了比各部分的名称。
我还知道了比、分数、除法之间的联系和区别。
板书设计
生活中的比
两个数相除又叫做两个数的比。
6 : 4
6
4
=
=6 ÷ 4
=1.5
…
前
项
…
后
项
…
比
值
读作:六比四
…
比
号
作业布置
完成课本“练一练”第1~4题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
