新课标北师大版六上7.1《百分数的应用(一)》课件(30张PPT)
文档属性
| 名称 | 新课标北师大版六上7.1《百分数的应用(一)》课件(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 11:25:30 | ||
图片预览









文档简介
(共30张PPT)
百分数的应用(一)
北师大版六年级上册
教学目标
1.学习目标描述:创设具体的情景,理解“增加百分之几”或“减少百分之几”的意义,学会用线段图分析数量关系,进而解答此类问题。
2.学习内容分析:本节核心内容是理解“增加百分之几和减少百分之几”的意义,提高学生运用百分数知识解决实际问题的能力。让学生带着问题探寻解决问题的方法。本课创设水结冰、冰化水的情景
教学目标
,理解增加百分之几和减少百分之几的意义,并由此及彼掌握解决此类问题的方法。并为后续的内容,较复杂的百分数应用题做好准备。
3.学科核心素养分析:通过创设具体的生活情境,体会百分数与现实生活的紧密联系,提高解决问题的能力,激发学生学习数学的兴趣,感受学习数学的价值,增强学生的应用意识。
新知导入
1.说说下面百分数表示的含义。
(1)六(1)班有50%的同学会游泳。
(2)地球上陆地面积大约占29%。
(3)残疾儿童入学率已超过60%。
表示班中会游泳的人数占班级总人数的50%。
表示地球上陆地面积大约占地球表面积的29%。
表示残疾儿童入学人数占总残疾人数的60%。
百分数表示一个数是另一数的百分之几。百分数也叫百分比,百分率。
新知导入
2.果园里有苹果树800棵,梨树有1000棵。苹果树的棵数是梨树的百分之几?
800÷1000=80%
答:苹果树棵数是梨树的80%。
求一个数是另一个数的百分之几,用除法。
新知讲解
水结成冰之后体积发生了什么变化?
有45cm3的水。
结冰以后体积约为50cm3。
水结成冰,体积会增加。
新知讲解
冰的体积比原来水的体积约增加了百分之几?
增加了多少?增加百分之几是什么意思?
可以画图试一试。
新知讲解
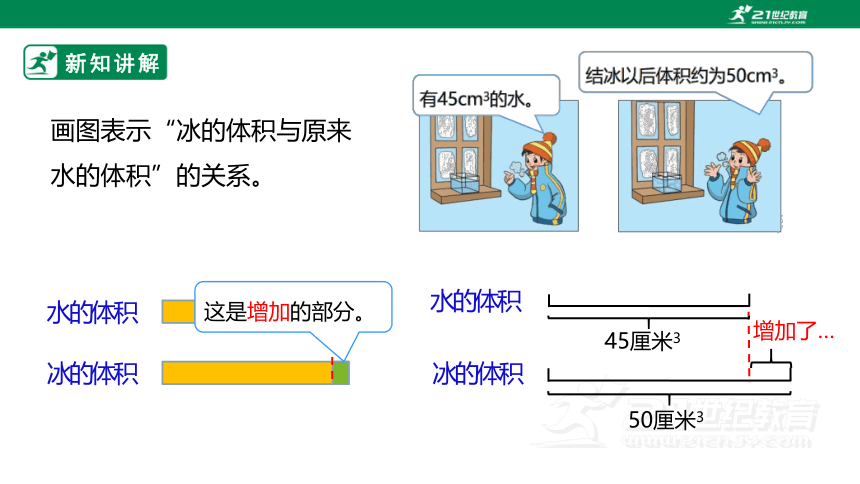
画图表示“冰的体积与原来水的体积”的关系。
水的体积
冰的体积
这是增加的部分。
水的体积
冰的体积
45厘米3
50厘米3
增加了…
新知讲解
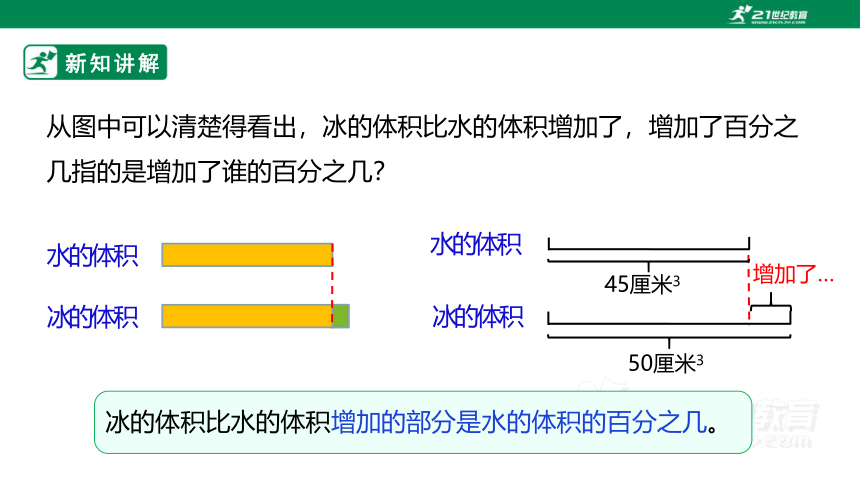
从图中可以清楚得看出,冰的体积比水的体积增加了,增加了百分之几指的是增加了谁的百分之几?
水的体积
冰的体积
水的体积
冰的体积
45厘米3
50厘米3
增加了…
冰的体积比水的体积增加的部分是水的体积的百分之几。
新知讲解
冰的体积比原来水的体积约增加了百分之几?列出算式解答。
先算增加了多少立方厘米。
(50-45)÷45
=5÷45
≈11.1%
答:冰的体积比原来水的体积约增加11.1%。
新知讲解
冰的体积比原来水的体积约增加了百分之几?列出算式解答。
还可以先算冰的体积是原来水的体积的百分之几。
50÷45≈111.1%
111.1%-100%=11%
答:冰的体积比原来水的体积约增加11.1%。
新知讲解
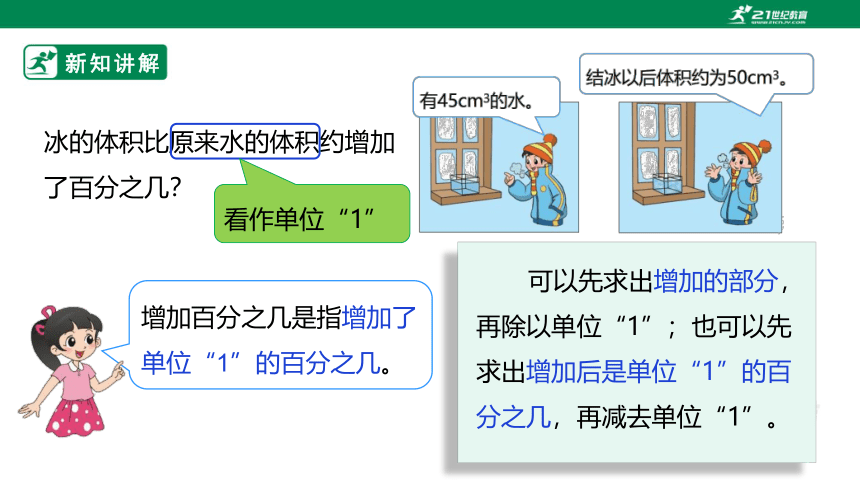
冰的体积比原来水的体积约增加了百分之几?
看作单位“1”
增加百分之几是指增加了单位“1”的百分之几。
可以先求出增加的部分,再除以单位“1”;也可以先求出增加后是单位“1”的百分之几,再减去单位“1”。
新知讲解
计算中遇到除不尽时,一般保留三位小数。(百分号前面的数保留一位小数)。
新知讲解
水的体积比冰的体积少百分之几
少了11.1%。
不对吧,我们还是画图看一看吧。
新知讲解
水的体积比冰的体积少百分之几
水的体积
冰的体积
这是减少的部分。
水的体积比冰的体积减少的部分是冰的体积的百分之几。
新知讲解
水的体积比冰的体积少百分之几
先算减少了多少立方厘米。
(50-45)÷50
=5÷50
=10%
答:水的体积比冰的体积少10%。
新知讲解
水的体积比冰的体积少百分之几
还可以先算水的体积是冰的百分之几。
45÷50=90%
1-90%=10%
答:水的体积比冰的体积少10%。
新知讲解
怎样解决求“减少百分之几”的问题?
可以先求出减少的部分,再除以单位“1”;也可以先求出减少后是单位“1”的百分之几,再用单位“1”去减。
新知讲解
A
B
降价32元
现价96元
降价50元
现价160元
哪种电水壶价格降得多?
一眼就看出来了,是B。
新知讲解
A
B
降价32元
现价96元
降价50元
现价160元
哪种水壶的价格降低的百分比多呢?
画一个图试试。
原价
现价
96元
32元
降低?%
元
原价
现价
160元
50元
降低?%
元
我发现:降低百分之几是指降低了原价的百分之几。
新知讲解
原价
现价
96元
32元
降低?%
元
原价
现价
160元
50元
降低?%
元
先求两种热水壶的原价,原价是现价与降价的和。
32÷(96+32)=25%
50÷(160+50)≈23.8%
答:B种电水壶价格降得多。
课堂练习
1.连一连。
5是4的百分之几? (5-4)÷5
4是5的百分之几? (5-4)÷4
5比4多百分之几? 5÷4
4比5少百分之几? 4÷5
课堂练习
2.军军去年体重30千克,今年增加到36千克,增加了百分之几?
(36-30)÷30
=6÷30
=20%
答:增加了20%。
课堂练习
3.某糖厂七月生产552吨糖,比计划多生产72吨,超产百分之几?
超产了计划的百分之几?
72÷(552-72)
=72÷480
=15%
答:超产15%。
课堂练习
4.拓展应用:火车从甲城到乙城原来需要16小时,提速后需要10小时,速度提高了百分之几?
此题把全程看作单位“1”,所以速度= 。
1
时间
( - )÷
1
10
1
16
1
16
3
80
1
16
= ÷
=60%
答:速度提高了60%。
课堂总结
通过今天的学习,你有哪些收获?
我会解决求一个数比另一个数多(或少)百分之几的应用题了。
我还知道可以用两数之差÷单位“1”来解答。
板书设计
百分数的应用(一)
——解决有关“增加(或减少)百分之几”的问题
冰的体积比原来水的体积约增加了多少?
(50-45)÷45 50 ÷45 ≈ 111.1%
=5÷45 111.1%-100%=11.1%
≈11.1%
答:冰的体积比原来水的体积约增加了11.1% 。
作业布置
完成课本“练一练”第1、2、3题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
百分数的应用(一)
北师大版六年级上册
教学目标
1.学习目标描述:创设具体的情景,理解“增加百分之几”或“减少百分之几”的意义,学会用线段图分析数量关系,进而解答此类问题。
2.学习内容分析:本节核心内容是理解“增加百分之几和减少百分之几”的意义,提高学生运用百分数知识解决实际问题的能力。让学生带着问题探寻解决问题的方法。本课创设水结冰、冰化水的情景
教学目标
,理解增加百分之几和减少百分之几的意义,并由此及彼掌握解决此类问题的方法。并为后续的内容,较复杂的百分数应用题做好准备。
3.学科核心素养分析:通过创设具体的生活情境,体会百分数与现实生活的紧密联系,提高解决问题的能力,激发学生学习数学的兴趣,感受学习数学的价值,增强学生的应用意识。
新知导入
1.说说下面百分数表示的含义。
(1)六(1)班有50%的同学会游泳。
(2)地球上陆地面积大约占29%。
(3)残疾儿童入学率已超过60%。
表示班中会游泳的人数占班级总人数的50%。
表示地球上陆地面积大约占地球表面积的29%。
表示残疾儿童入学人数占总残疾人数的60%。
百分数表示一个数是另一数的百分之几。百分数也叫百分比,百分率。
新知导入
2.果园里有苹果树800棵,梨树有1000棵。苹果树的棵数是梨树的百分之几?
800÷1000=80%
答:苹果树棵数是梨树的80%。
求一个数是另一个数的百分之几,用除法。
新知讲解
水结成冰之后体积发生了什么变化?
有45cm3的水。
结冰以后体积约为50cm3。
水结成冰,体积会增加。
新知讲解
冰的体积比原来水的体积约增加了百分之几?
增加了多少?增加百分之几是什么意思?
可以画图试一试。
新知讲解
画图表示“冰的体积与原来水的体积”的关系。
水的体积
冰的体积
这是增加的部分。
水的体积
冰的体积
45厘米3
50厘米3
增加了…
新知讲解
从图中可以清楚得看出,冰的体积比水的体积增加了,增加了百分之几指的是增加了谁的百分之几?
水的体积
冰的体积
水的体积
冰的体积
45厘米3
50厘米3
增加了…
冰的体积比水的体积增加的部分是水的体积的百分之几。
新知讲解
冰的体积比原来水的体积约增加了百分之几?列出算式解答。
先算增加了多少立方厘米。
(50-45)÷45
=5÷45
≈11.1%
答:冰的体积比原来水的体积约增加11.1%。
新知讲解
冰的体积比原来水的体积约增加了百分之几?列出算式解答。
还可以先算冰的体积是原来水的体积的百分之几。
50÷45≈111.1%
111.1%-100%=11%
答:冰的体积比原来水的体积约增加11.1%。
新知讲解
冰的体积比原来水的体积约增加了百分之几?
看作单位“1”
增加百分之几是指增加了单位“1”的百分之几。
可以先求出增加的部分,再除以单位“1”;也可以先求出增加后是单位“1”的百分之几,再减去单位“1”。
新知讲解
计算中遇到除不尽时,一般保留三位小数。(百分号前面的数保留一位小数)。
新知讲解
水的体积比冰的体积少百分之几
少了11.1%。
不对吧,我们还是画图看一看吧。
新知讲解
水的体积比冰的体积少百分之几
水的体积
冰的体积
这是减少的部分。
水的体积比冰的体积减少的部分是冰的体积的百分之几。
新知讲解
水的体积比冰的体积少百分之几
先算减少了多少立方厘米。
(50-45)÷50
=5÷50
=10%
答:水的体积比冰的体积少10%。
新知讲解
水的体积比冰的体积少百分之几
还可以先算水的体积是冰的百分之几。
45÷50=90%
1-90%=10%
答:水的体积比冰的体积少10%。
新知讲解
怎样解决求“减少百分之几”的问题?
可以先求出减少的部分,再除以单位“1”;也可以先求出减少后是单位“1”的百分之几,再用单位“1”去减。
新知讲解
A
B
降价32元
现价96元
降价50元
现价160元
哪种电水壶价格降得多?
一眼就看出来了,是B。
新知讲解
A
B
降价32元
现价96元
降价50元
现价160元
哪种水壶的价格降低的百分比多呢?
画一个图试试。
原价
现价
96元
32元
降低?%
元
原价
现价
160元
50元
降低?%
元
我发现:降低百分之几是指降低了原价的百分之几。
新知讲解
原价
现价
96元
32元
降低?%
元
原价
现价
160元
50元
降低?%
元
先求两种热水壶的原价,原价是现价与降价的和。
32÷(96+32)=25%
50÷(160+50)≈23.8%
答:B种电水壶价格降得多。
课堂练习
1.连一连。
5是4的百分之几? (5-4)÷5
4是5的百分之几? (5-4)÷4
5比4多百分之几? 5÷4
4比5少百分之几? 4÷5
课堂练习
2.军军去年体重30千克,今年增加到36千克,增加了百分之几?
(36-30)÷30
=6÷30
=20%
答:增加了20%。
课堂练习
3.某糖厂七月生产552吨糖,比计划多生产72吨,超产百分之几?
超产了计划的百分之几?
72÷(552-72)
=72÷480
=15%
答:超产15%。
课堂练习
4.拓展应用:火车从甲城到乙城原来需要16小时,提速后需要10小时,速度提高了百分之几?
此题把全程看作单位“1”,所以速度= 。
1
时间
( - )÷
1
10
1
16
1
16
3
80
1
16
= ÷
=60%
答:速度提高了60%。
课堂总结
通过今天的学习,你有哪些收获?
我会解决求一个数比另一个数多(或少)百分之几的应用题了。
我还知道可以用两数之差÷单位“1”来解答。
板书设计
百分数的应用(一)
——解决有关“增加(或减少)百分之几”的问题
冰的体积比原来水的体积约增加了多少?
(50-45)÷45 50 ÷45 ≈ 111.1%
=5÷45 111.1%-100%=11.1%
≈11.1%
答:冰的体积比原来水的体积约增加了11.1% 。
作业布置
完成课本“练一练”第1、2、3题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
