2.2.1 配方法(1)课件(共23张PPT)
文档属性
| 名称 | 2.2.1 配方法(1)课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 28.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 07:13:40 | ||
图片预览








文档简介
(共23张PPT)
2.2.1 配方法(1)
湘教版 九年级上
1. 理解一元二次方程的根的概念.
2. 能用直接开平方法求具有完全平方结构的一元二次方
程的根.
3. 体会整体思想在解一元二次方程中的应用,提高知识
运用能力.
新知导入
填空:
1. 若r =a,则r是a的一个 .
2. 正数有且只有两个 的平方根.0的平方根
是 , 负数 平方根.
3. 49的算术平方根是 ,7的平方根是 .
4. = ,= .
互为相反数
没有
平方根
0
7
新知导入
做一做:
5. 解方程:
(1) 2-x=; (2) 2x+1=.
6. 的算术平方根是( )
A. 4 B. ±4 C. 2 D. ±2
新知讲解
如何解本章2.1节“动脑筋”中的方程: x ﹣2500=0呢?
把方程 x ﹣2500=0写成
x =2500.
这表明 :x是 2500的平方根。
根据平方根的意义,得
或
因此原方程的解为
x =50,x =﹣50.
因为方程x ﹣2500=0是为了求实际问题中圆的半径,所以x =﹣50不合题意,应当舍去。而 x =50符合题意,因此该圆的半径为50cm.
一元二次方程的解也叫作一元二次方程的根.
新知讲解
例1 解方程:4x ﹣25=0.
解 原方程可化为
根据平方根的意义,得
或
因此,原方程的根为
例题讲解
如何解方程: (1+x) =81?
若把1+x看作一个整体,则由(1+x) =81,得
1+
或
1+
即 1+x=9或1+x=﹣9.
解得 x =8,x =﹣10.
新知讲解
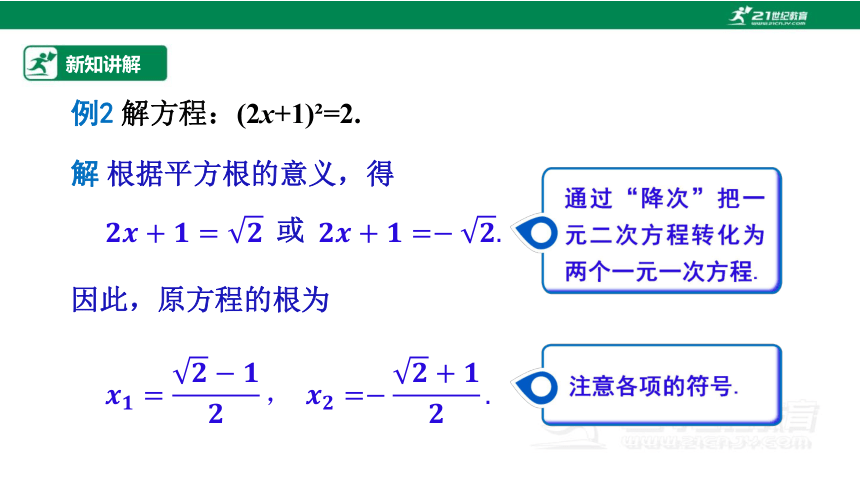
例2 解方程:(2x+1) =2.
解 根据平方根的意义,得
因此,原方程的根为
或
通过“降次”把一元二次方程转化为两个一元一次方程.
注意各项的符号.
新知讲解
解方程: 4(x+1) -25=0.
解 移项,得
4(x+1) =25.
方程两边都除以4,得
新知讲解
根据平方根的意义,得
因此,原方程的根为
或
新知讲解
1. 利用平方根的意义解方程,最容易开平方求出方程的根的变形是( )
A. B.
C. D.
C
巩固练习
2. 一元二次方程(x+1) =5的根是 ( )
A. ,
B. ,
C. ,
D. ,
B
巩固练习
3. (2021泸县模拟)已知关于x的方程x +x+2a-4=0的一个根是-1,则a的值是( )
A. -2 B. -1
C. 1 D. 2
D
解析将方程的一个根x=-1代入方程x +x+2a-4=0,得关于a的方程2a-4=0,解得a=2,故选D.
巩固练习
4. 若方程(x+1) =a-1有实数根,则a的取值范围是( )
A. a<1 B. a>1
C. a≤1 D. a≥1
D
解析:根据数的平方和平方根的性质,可得a-1≥0,
解得 a≥1,故选D.
巩固练习
课堂总结
1. 用直接开平方法解一元二次方程的基本想法是什么?
把一个一元二次方程通过“降次”转化为两个一元一次方程,再分别解这两个一元一次方程。
2. 用直接开平方法解一元二次方程有哪些步骤?
①变形:化成x =a或(ax+b) =c的形式.
②开平方:把原方程化成两个一元一次方程.
③解出原方程的根:注意不要遗漏其中的一个负根.
作业布置
课后练习第1、2题:
1. 解下列方程:
(1)9x =49; (2)36﹣x =0;
(3)(x+1) ﹣36=0; (4)9(1-2x) -16=0.
答案:
(1)
(2)
作业布置
(3)(x+3) ﹣36=0; (4)9(1-2x) -16=0.
解 (3)移项得
解得
(x+3) =36.
开平方,得
x+3=6或x+3=-6.
x1=3,x2=-9.
(3)(x+1) ﹣36=0; (4)9(1-2x) -16=0.
(4)原方程可化为
开平方得
或
故原方程的根为
作业布置
2. (古代数学问题)直田七亩半,忘了长和短.
记得立契时,长阔争一半.
今问俊明公,此法如何算.
意思是:有一块面积为7亩半的长方形田,忘了长与宽各是多少.只记得在立契约的时候说过,宽是长的一半.现在请你帮他算出它的长和宽各是多少步(一亩=240步 ).
思路:先设未知数,根据长方形的面积公式列出方程,再解方程,最后根据实际确定答案.
作业布置
解 设这块长方形田的宽为x步,则长为2x步.根据田的面积=7亩半,可列方程
x·2x=7.5×240
2x =1800.
化简得
解得
x =30,x =-30(负值不合题意,舍去).
∴ x=30,则2x=60.
所以田的长为60步,宽为30步.
即
x =900.
作业布置
https://www.21cnjy.com/help/help_extract.php
2.2.1 配方法(1)
湘教版 九年级上
1. 理解一元二次方程的根的概念.
2. 能用直接开平方法求具有完全平方结构的一元二次方
程的根.
3. 体会整体思想在解一元二次方程中的应用,提高知识
运用能力.
新知导入
填空:
1. 若r =a,则r是a的一个 .
2. 正数有且只有两个 的平方根.0的平方根
是 , 负数 平方根.
3. 49的算术平方根是 ,7的平方根是 .
4. = ,= .
互为相反数
没有
平方根
0
7
新知导入
做一做:
5. 解方程:
(1) 2-x=; (2) 2x+1=.
6. 的算术平方根是( )
A. 4 B. ±4 C. 2 D. ±2
新知讲解
如何解本章2.1节“动脑筋”中的方程: x ﹣2500=0呢?
把方程 x ﹣2500=0写成
x =2500.
这表明 :x是 2500的平方根。
根据平方根的意义,得
或
因此原方程的解为
x =50,x =﹣50.
因为方程x ﹣2500=0是为了求实际问题中圆的半径,所以x =﹣50不合题意,应当舍去。而 x =50符合题意,因此该圆的半径为50cm.
一元二次方程的解也叫作一元二次方程的根.
新知讲解
例1 解方程:4x ﹣25=0.
解 原方程可化为
根据平方根的意义,得
或
因此,原方程的根为
例题讲解
如何解方程: (1+x) =81?
若把1+x看作一个整体,则由(1+x) =81,得
1+
或
1+
即 1+x=9或1+x=﹣9.
解得 x =8,x =﹣10.
新知讲解
例2 解方程:(2x+1) =2.
解 根据平方根的意义,得
因此,原方程的根为
或
通过“降次”把一元二次方程转化为两个一元一次方程.
注意各项的符号.
新知讲解
解方程: 4(x+1) -25=0.
解 移项,得
4(x+1) =25.
方程两边都除以4,得
新知讲解
根据平方根的意义,得
因此,原方程的根为
或
新知讲解
1. 利用平方根的意义解方程,最容易开平方求出方程的根的变形是( )
A. B.
C. D.
C
巩固练习
2. 一元二次方程(x+1) =5的根是 ( )
A. ,
B. ,
C. ,
D. ,
B
巩固练习
3. (2021泸县模拟)已知关于x的方程x +x+2a-4=0的一个根是-1,则a的值是( )
A. -2 B. -1
C. 1 D. 2
D
解析将方程的一个根x=-1代入方程x +x+2a-4=0,得关于a的方程2a-4=0,解得a=2,故选D.
巩固练习
4. 若方程(x+1) =a-1有实数根,则a的取值范围是( )
A. a<1 B. a>1
C. a≤1 D. a≥1
D
解析:根据数的平方和平方根的性质,可得a-1≥0,
解得 a≥1,故选D.
巩固练习
课堂总结
1. 用直接开平方法解一元二次方程的基本想法是什么?
把一个一元二次方程通过“降次”转化为两个一元一次方程,再分别解这两个一元一次方程。
2. 用直接开平方法解一元二次方程有哪些步骤?
①变形:化成x =a或(ax+b) =c的形式.
②开平方:把原方程化成两个一元一次方程.
③解出原方程的根:注意不要遗漏其中的一个负根.
作业布置
课后练习第1、2题:
1. 解下列方程:
(1)9x =49; (2)36﹣x =0;
(3)(x+1) ﹣36=0; (4)9(1-2x) -16=0.
答案:
(1)
(2)
作业布置
(3)(x+3) ﹣36=0; (4)9(1-2x) -16=0.
解 (3)移项得
解得
(x+3) =36.
开平方,得
x+3=6或x+3=-6.
x1=3,x2=-9.
(3)(x+1) ﹣36=0; (4)9(1-2x) -16=0.
(4)原方程可化为
开平方得
或
故原方程的根为
作业布置
2. (古代数学问题)直田七亩半,忘了长和短.
记得立契时,长阔争一半.
今问俊明公,此法如何算.
意思是:有一块面积为7亩半的长方形田,忘了长与宽各是多少.只记得在立契约的时候说过,宽是长的一半.现在请你帮他算出它的长和宽各是多少步(一亩=240步 ).
思路:先设未知数,根据长方形的面积公式列出方程,再解方程,最后根据实际确定答案.
作业布置
解 设这块长方形田的宽为x步,则长为2x步.根据田的面积=7亩半,可列方程
x·2x=7.5×240
2x =1800.
化简得
解得
x =30,x =-30(负值不合题意,舍去).
∴ x=30,则2x=60.
所以田的长为60步,宽为30步.
即
x =900.
作业布置
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
