2.5 一元二次方程的应用(2)课件(共25张PPT)
文档属性
| 名称 | 2.5 一元二次方程的应用(2)课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
2.5 一元二次方程的应用(2)
湘教版 九年级上
教学目标
1. 能运用一元二次方程解决与面积相关的问题.
2. 能运用一元二次方程解决动点问题.
3. 提高学生综合分析问题、运用方程解决问题的能力.
4. 体验借助一元二次方程实现数形结合的应用价值.
温故知新
说一说:
1. 运用一元二次方程模型解决实际问题的步骤有哪些?这些步骤中,应注意些什么?
如何利用一元二次方程解决几何图形中的问题呢?
2. 利用一元二次方程求变化率问题、利用一元二次方程解决利润问题的过程中,所涉及的等量关系分别有哪些?
新知讲解
长方
如图,在一长为40m、宽为28m的矩形铁皮的四角截去四个全等的小正方形后,折成一个无盖的长方体盒子. 若
已知长方体盒子的底面积为364cm ,求截去的四个小正方形的边长.
分析 将铁皮截去四个小正方形后,可以得到右图.这个长方形盒子的底面积就是右图中的阴影部分,因此本问题涉及的等量关系是:
盒子的底面积=盒子的底面长×盒子的底面宽.
设截去的小正方形的边长为xcm,则无盖长方体盒子的底面长与宽分别为 cm, cm,根据等量关系,可以列出方程
(28-2x)
(40-2x)
新知讲解
即 2(20-x)·2(14-x)=364.
解得
x =27,x =7.
如果截去的小正方形的边长为27cm,那么左上角和右上角的两个小正方形的边长之和为54cm,这超过了矩形铁皮的长度(40cm).因此x1=27不合题意,应当舍去.
(40-2x)(28-2x)=364.
方程两边都除以4,得 (20-x)·(14-x)=91.
去括号并整理,得
x -34x+189=0.
因此,截去的小正方形的边长为7cm.
新知讲解
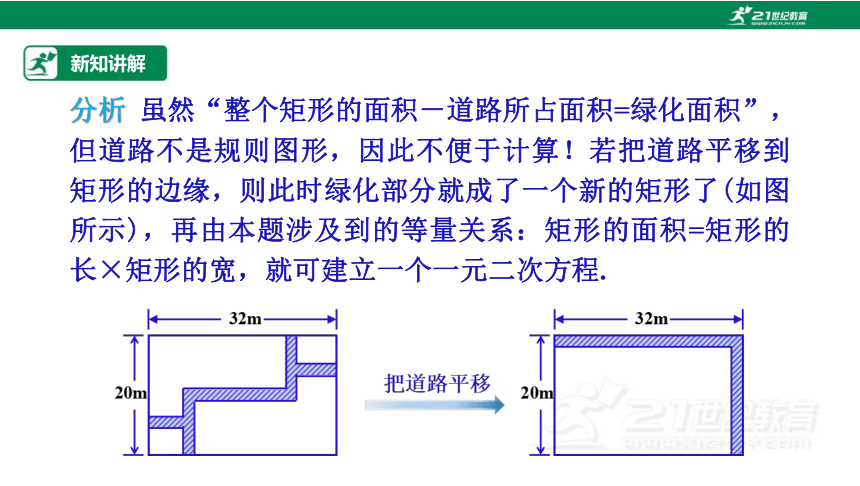
例3 如图,一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分),余下部分进行了绿化.若已知绿化面积为540m ,求道路的宽.
新知讲解
分析 虽然“整个矩形的面积-道路所占面积=绿化面积”,但道路不是规则图形,因此不便于计算!若把道路平移到矩形的边缘,则此时绿化部分就成了一个新的矩形了(如图所示),再由本题涉及到的等量关系:矩形的面积=矩形的长×矩形的宽,就可建立一个一元二次方程.
新知讲解
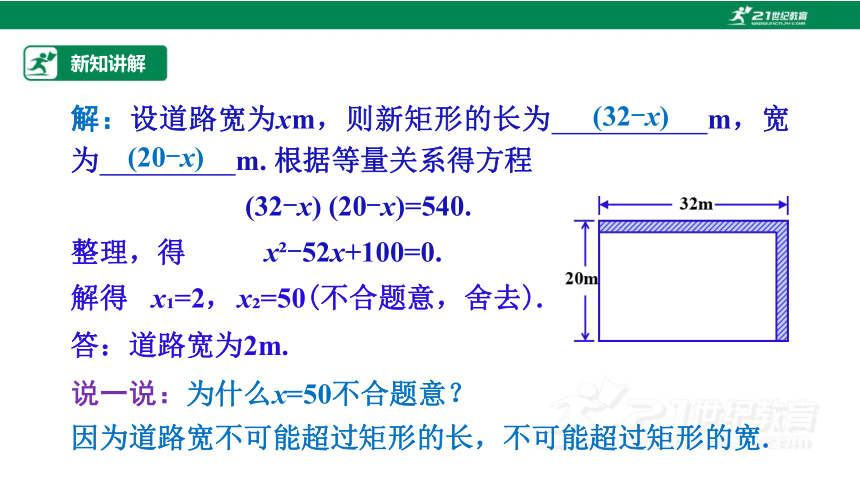
解:设道路宽为xm,则新矩形的长为 m,宽为 m. 根据等量关系得方程
(32-x) (20-x)=540.
整理,得
x -52x+100=0.
解得
x =2,
x =50(不合题意,舍去).
答:道路宽为2m.
(32-x)
(20-x)
说一说:为什么x=50不合题意?
因为道路宽不可能超过矩形的长,不可能超过矩形的宽.
新知讲解
合作讨论
如何运用一元二次方程解决面积问题?
运用一元二次方程解决面积问题的方法:
①根据问题设一条线段的长(如设为x);
②用含x的代数式表示底和高(或长和宽等);
③根据图形,选择面积公式列出一元一次方程;
④解一元二次方程,并根据图形确定实际问题的解.
新知讲解
例4 如图所示,在△ABC中,∠C=90°,AC=
6cm,BC=8cm.点P沿AC边从点A向终点C以1cm/s的速度移动;同时点Q沿CB边从点C向终点B以2cm/s的速度移动,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后,可使△PCQ的面积为9cm
分析 设点P,Q出发的时间为xs,然后用含x的代数式表示△PCQ的直角边PC,CQ的长,即可结合直角三角形的面积公式根据等量关系列出一元二次方程求解.
例4 如图所示,在△ABC中,∠C=90°,AC=
6cm,BC=8cm.点P沿AC边从点A向终点C以1cm/s的速度移动;同时点Q沿CB边从点C向终点B以2cm/s的速度移动,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后,可使△PCQ的面积为9cm
解 设点P,Q出发xs后可使△PCQ的面积为9cm .根据题意得AP= cm, PC= cm,CQ = cm.
x
(6-x)
2x
新知讲解
则由S△POQ=PC·CQ可得
整理,得
x -6x+9=0.
答:点P ,Q出发3秒后,可使△PCQ的面积为9cm .
解得
x =x =3.
新知讲解
合作讨论
如何运用一元二次方程解决动点问题?
运用一元二次方程解决动点问题的方法:
①设运动时间为x(单位:min、s等);
②根据路程=速度×时间,用含x的代数式表示相关线段的长;
③根据图形的性质或公式列出一元二次方程;
④解一元二次方程,并根据图形确定实际问题的解.
巩固练习
1. (江西模拟)如图,为美化校园环境,学校打算在长为30m、宽为20m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成宽为am的通道.若花圃的面积恰好等于264m ,则通道的宽a= m.
4
点拨 根据图形可列方程:(30-2a) (20-2a)=264,将方程整理后,即可结合实际求出问题的解.
2. (天宁区月考)如图,在矩形ABCD中,AB=12cm,BC=6cm,点P从点A出发沿AB以2cm/s的速度向点B运动;同时点Q从点B出发沿BC以2cm/s的速度向点C运动,且当点P到达点B时,点Q也停止运动,当△PQC的面积等于16cm时,运动时间为 s.
2
巩固练习
课堂总结
1. 如何运用一元二次方程解决面积问题?
①根据问题设一条线段的长(如设为x);
②用含x的代数式表示底和高(或长和宽等);
③根据图形,选择面积公式列出一元一次方程;
④解一元二次方程,并根据图形确定实际问题的解
课堂总结
2. 如何运用一元二次方程解决面积问题?
①设运动时间为x(单位:min、s等);
②根据路程=速度×时间,用含x的代数式表示相关线段的长;
③根据图形的性质和公式列出一元二次方程;
④解一元二次方程,并根据图形确定实际问题的解.
课堂总结
3. 用一元二次方程解决几何图形问题的应注意什么?
①设好适当的未知数;
②用所设未知数表示有关线段;
③根据图形性质及公式(如面积公式)列出一元二次方程;
④解方程,根据图形和题意确定正确的答案.
1. 如图,在长为100m、宽为80m的矩形地面上要修建两条宽度相等且互相垂直的道路,剩余部分绿化.若要使绿化面积为7644m ,则道路的宽应为多少米
分析 把两条道路平移到矩形边缘,得到绿化部分是一个新的矩形,再利用矩形的面积公式:面积=长×宽,即可列出一元二次方程求解.
作业指导
作业指导
解:把道路平移得到新的矩形如图,设道路宽为xm,则新矩形的长为 m,宽为 m. 根据等量关系得方程
(100-x) (80-x)=7644.
整理,得
x -180x+356=0.
解得
x =2,
x =178(舍去).
答:道路宽为2m.
(100-x)
(80-x)
所以
(x-2) (x-178)=0.
2. 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P,Q同时从A,B两点出发,分别沿AC,BC向终点C移动,它们的速度都是1cm/s,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后,可使△PCQ的面积为△ABC 面积的一半
作业指导
解:设点P,Q出发x秒后,可使△PCQ的面积为△ABC 面积的一半.由题意得
∴
S△ABC=AC·BC=×8×6=24(cm ).
S△PCQ=PC·CQ=(cm ).
作业指导
整理,得 x -14x+24=0.
解得
x =2,
x =12(舍去).
因此,点P,Q出发2秒后,可使△PCQ的面积为△ABC 面积的一半.
因式分解,得
(x-2) (x-12)=0.
作业指导
https://www.21cnjy.com/help/help_extract.php
2.5 一元二次方程的应用(2)
湘教版 九年级上
教学目标
1. 能运用一元二次方程解决与面积相关的问题.
2. 能运用一元二次方程解决动点问题.
3. 提高学生综合分析问题、运用方程解决问题的能力.
4. 体验借助一元二次方程实现数形结合的应用价值.
温故知新
说一说:
1. 运用一元二次方程模型解决实际问题的步骤有哪些?这些步骤中,应注意些什么?
如何利用一元二次方程解决几何图形中的问题呢?
2. 利用一元二次方程求变化率问题、利用一元二次方程解决利润问题的过程中,所涉及的等量关系分别有哪些?
新知讲解
长方
如图,在一长为40m、宽为28m的矩形铁皮的四角截去四个全等的小正方形后,折成一个无盖的长方体盒子. 若
已知长方体盒子的底面积为364cm ,求截去的四个小正方形的边长.
分析 将铁皮截去四个小正方形后,可以得到右图.这个长方形盒子的底面积就是右图中的阴影部分,因此本问题涉及的等量关系是:
盒子的底面积=盒子的底面长×盒子的底面宽.
设截去的小正方形的边长为xcm,则无盖长方体盒子的底面长与宽分别为 cm, cm,根据等量关系,可以列出方程
(28-2x)
(40-2x)
新知讲解
即 2(20-x)·2(14-x)=364.
解得
x =27,x =7.
如果截去的小正方形的边长为27cm,那么左上角和右上角的两个小正方形的边长之和为54cm,这超过了矩形铁皮的长度(40cm).因此x1=27不合题意,应当舍去.
(40-2x)(28-2x)=364.
方程两边都除以4,得 (20-x)·(14-x)=91.
去括号并整理,得
x -34x+189=0.
因此,截去的小正方形的边长为7cm.
新知讲解
例3 如图,一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分),余下部分进行了绿化.若已知绿化面积为540m ,求道路的宽.
新知讲解
分析 虽然“整个矩形的面积-道路所占面积=绿化面积”,但道路不是规则图形,因此不便于计算!若把道路平移到矩形的边缘,则此时绿化部分就成了一个新的矩形了(如图所示),再由本题涉及到的等量关系:矩形的面积=矩形的长×矩形的宽,就可建立一个一元二次方程.
新知讲解
解:设道路宽为xm,则新矩形的长为 m,宽为 m. 根据等量关系得方程
(32-x) (20-x)=540.
整理,得
x -52x+100=0.
解得
x =2,
x =50(不合题意,舍去).
答:道路宽为2m.
(32-x)
(20-x)
说一说:为什么x=50不合题意?
因为道路宽不可能超过矩形的长,不可能超过矩形的宽.
新知讲解
合作讨论
如何运用一元二次方程解决面积问题?
运用一元二次方程解决面积问题的方法:
①根据问题设一条线段的长(如设为x);
②用含x的代数式表示底和高(或长和宽等);
③根据图形,选择面积公式列出一元一次方程;
④解一元二次方程,并根据图形确定实际问题的解.
新知讲解
例4 如图所示,在△ABC中,∠C=90°,AC=
6cm,BC=8cm.点P沿AC边从点A向终点C以1cm/s的速度移动;同时点Q沿CB边从点C向终点B以2cm/s的速度移动,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后,可使△PCQ的面积为9cm
分析 设点P,Q出发的时间为xs,然后用含x的代数式表示△PCQ的直角边PC,CQ的长,即可结合直角三角形的面积公式根据等量关系列出一元二次方程求解.
例4 如图所示,在△ABC中,∠C=90°,AC=
6cm,BC=8cm.点P沿AC边从点A向终点C以1cm/s的速度移动;同时点Q沿CB边从点C向终点B以2cm/s的速度移动,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后,可使△PCQ的面积为9cm
解 设点P,Q出发xs后可使△PCQ的面积为9cm .根据题意得AP= cm, PC= cm,CQ = cm.
x
(6-x)
2x
新知讲解
则由S△POQ=PC·CQ可得
整理,得
x -6x+9=0.
答:点P ,Q出发3秒后,可使△PCQ的面积为9cm .
解得
x =x =3.
新知讲解
合作讨论
如何运用一元二次方程解决动点问题?
运用一元二次方程解决动点问题的方法:
①设运动时间为x(单位:min、s等);
②根据路程=速度×时间,用含x的代数式表示相关线段的长;
③根据图形的性质或公式列出一元二次方程;
④解一元二次方程,并根据图形确定实际问题的解.
巩固练习
1. (江西模拟)如图,为美化校园环境,学校打算在长为30m、宽为20m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成宽为am的通道.若花圃的面积恰好等于264m ,则通道的宽a= m.
4
点拨 根据图形可列方程:(30-2a) (20-2a)=264,将方程整理后,即可结合实际求出问题的解.
2. (天宁区月考)如图,在矩形ABCD中,AB=12cm,BC=6cm,点P从点A出发沿AB以2cm/s的速度向点B运动;同时点Q从点B出发沿BC以2cm/s的速度向点C运动,且当点P到达点B时,点Q也停止运动,当△PQC的面积等于16cm时,运动时间为 s.
2
巩固练习
课堂总结
1. 如何运用一元二次方程解决面积问题?
①根据问题设一条线段的长(如设为x);
②用含x的代数式表示底和高(或长和宽等);
③根据图形,选择面积公式列出一元一次方程;
④解一元二次方程,并根据图形确定实际问题的解
课堂总结
2. 如何运用一元二次方程解决面积问题?
①设运动时间为x(单位:min、s等);
②根据路程=速度×时间,用含x的代数式表示相关线段的长;
③根据图形的性质和公式列出一元二次方程;
④解一元二次方程,并根据图形确定实际问题的解.
课堂总结
3. 用一元二次方程解决几何图形问题的应注意什么?
①设好适当的未知数;
②用所设未知数表示有关线段;
③根据图形性质及公式(如面积公式)列出一元二次方程;
④解方程,根据图形和题意确定正确的答案.
1. 如图,在长为100m、宽为80m的矩形地面上要修建两条宽度相等且互相垂直的道路,剩余部分绿化.若要使绿化面积为7644m ,则道路的宽应为多少米
分析 把两条道路平移到矩形边缘,得到绿化部分是一个新的矩形,再利用矩形的面积公式:面积=长×宽,即可列出一元二次方程求解.
作业指导
作业指导
解:把道路平移得到新的矩形如图,设道路宽为xm,则新矩形的长为 m,宽为 m. 根据等量关系得方程
(100-x) (80-x)=7644.
整理,得
x -180x+356=0.
解得
x =2,
x =178(舍去).
答:道路宽为2m.
(100-x)
(80-x)
所以
(x-2) (x-178)=0.
2. 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P,Q同时从A,B两点出发,分别沿AC,BC向终点C移动,它们的速度都是1cm/s,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后,可使△PCQ的面积为△ABC 面积的一半
作业指导
解:设点P,Q出发x秒后,可使△PCQ的面积为△ABC 面积的一半.由题意得
∴
S△ABC=AC·BC=×8×6=24(cm ).
S△PCQ=PC·CQ=(cm ).
作业指导
整理,得 x -14x+24=0.
解得
x =2,
x =12(舍去).
因此,点P,Q出发2秒后,可使△PCQ的面积为△ABC 面积的一半.
因式分解,得
(x-2) (x-12)=0.
作业指导
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
