第三章 简单的几何图形 单元测试卷(Word版,含解析)
文档属性
| 名称 | 第三章 简单的几何图形 单元测试卷(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 364.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 16:29:25 | ||
图片预览

文档简介
第三章 简单的几何图形 单元测试卷
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
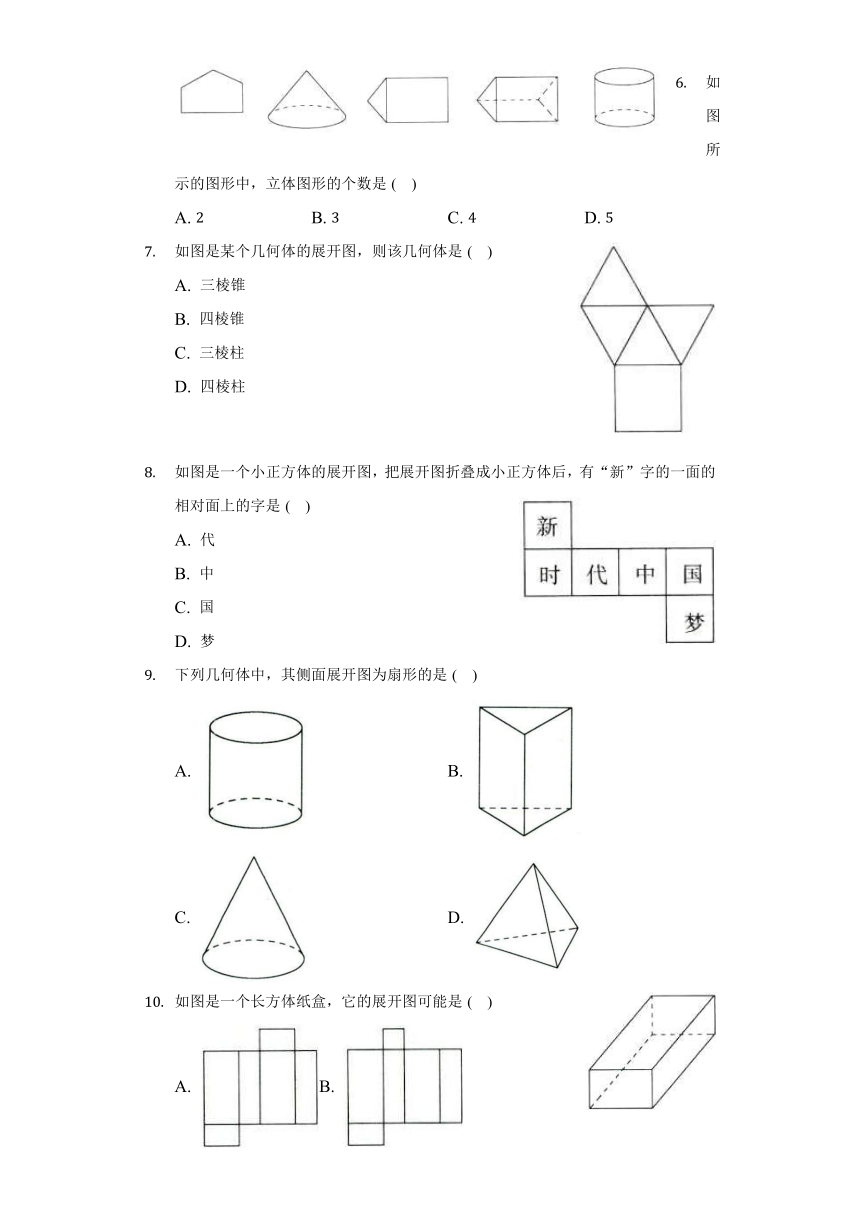
如图是一个正方体的表面展开图,图中的“你”的相对面是( )
A. 顺 B. 利 C. 一 D. 祝
下列说法正确的是( )
A. 两条互相平行的直线可能有交点
B. 两条直线相交,有且只有一个公共点
C. 平面内过一点可能有两条直线与已知直线垂直
D. 直线外一点与直线上各点连接的所有线段中,垂线段不一定最短
在同一平面内,两直线的位置关系必是( )
A. 相交 B. 平行 C. 垂直或平行 D. 相交或平行
下列说法中正确的是( )
A. 两条不相交的直线是平行线
B. 同一平面内,两条不相交的线段是平行线
C. 同一平面内,两条不相交的射线是平行线
D. 两条射线平行,是指它们所在的直线平行
下列图形中,线段的长表示点到直线距离的是( )
A. B.
C. D.
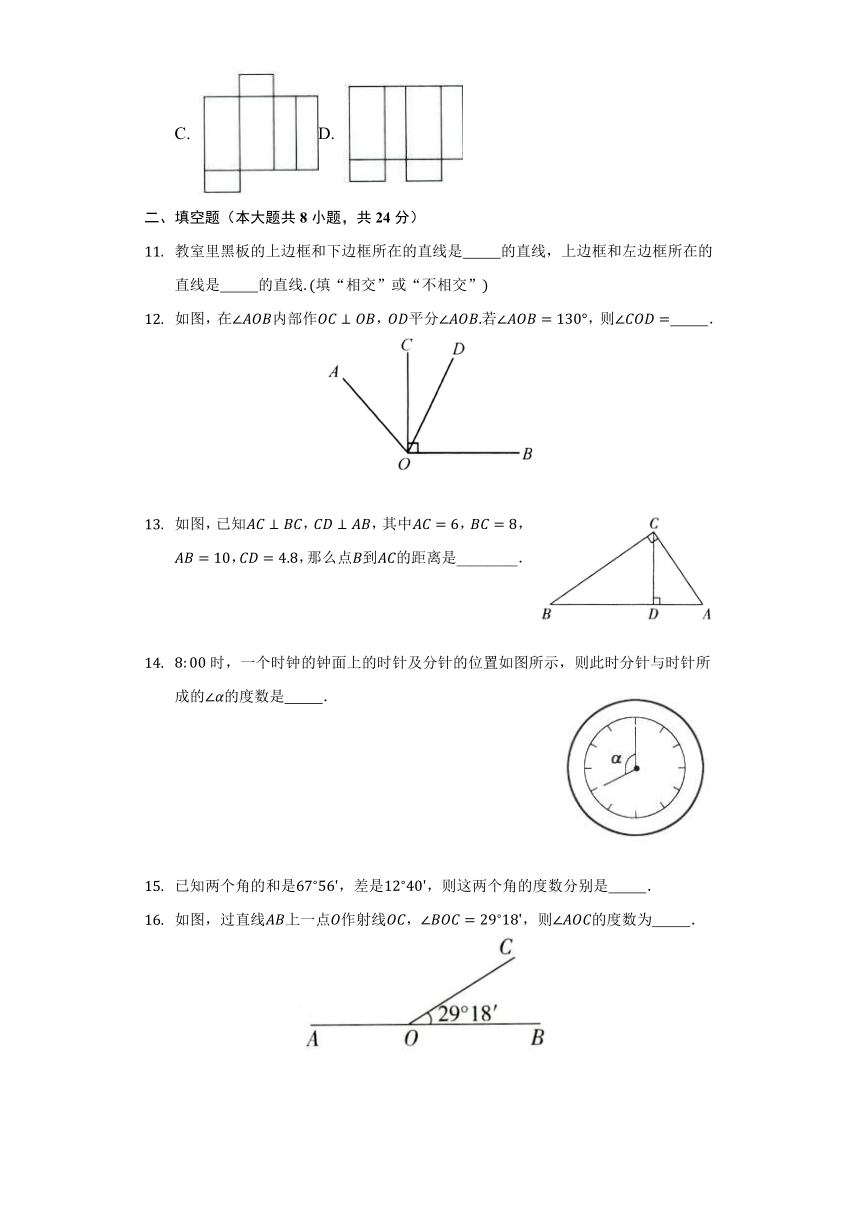
如图所示的图形中,立体图形的个数是( )
A. B. C. D.
如图是某个几何体的展开图,则该几何体是( )
A. 三棱锥
B. 四棱锥
C. 三棱柱
D. 四棱柱
如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“新”字的一面的相对面上的字是( )
A. 代
B. 中
C. 国
D. 梦
下列几何体中,其侧面展开图为扇形的是( )
A. B.
C. D.
如图是一个长方体纸盒,它的展开图可能是( )
A. B.
C. D.
二、填空题(本大题共8小题,共24分)
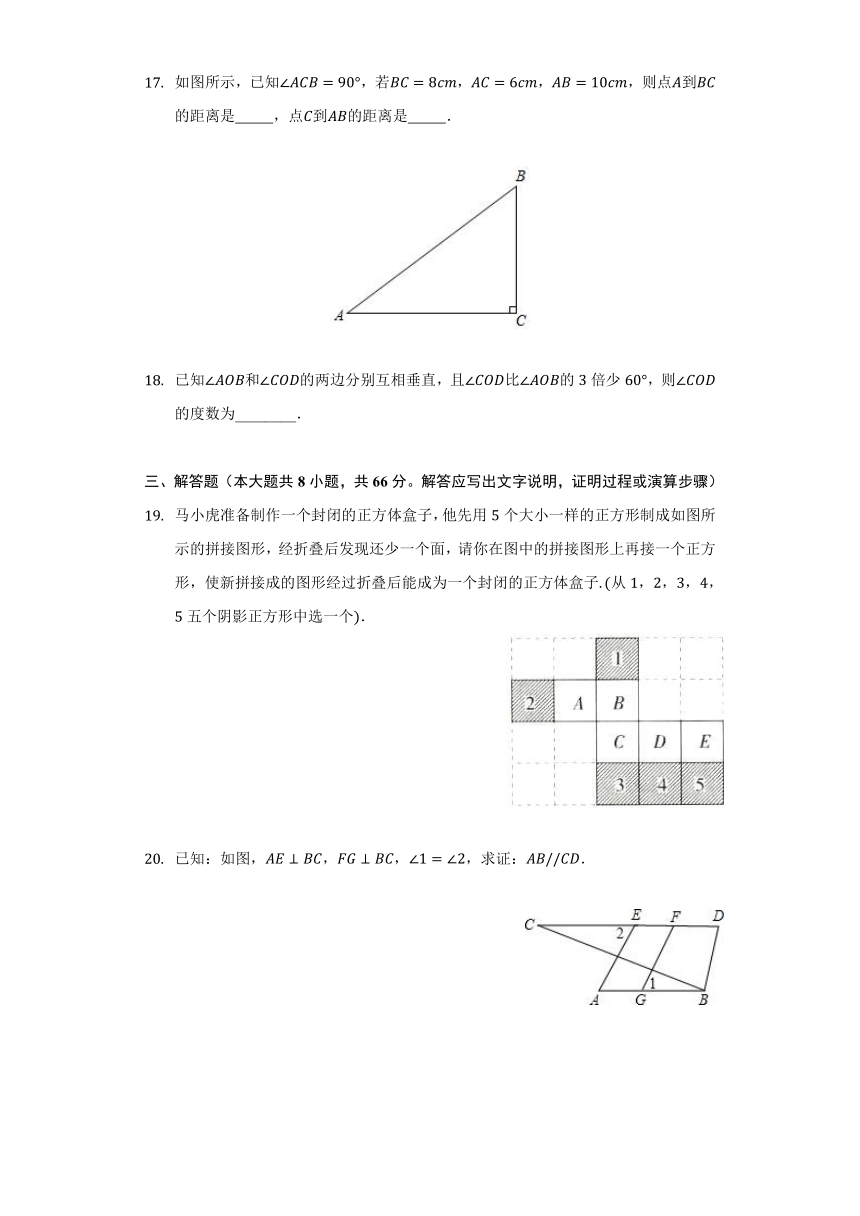
教室里黑板的上边框和下边框所在的直线是 的直线,上边框和左边框所在的直线是 的直线填“相交”或“不相交”
如图,在内部作,平分若,则 .
如图,已知,,其中,,,,那么点到的距离是________.
时,一个时钟的钟面上的时针及分针的位置如图所示,则此时分针与时针所成的的度数是 .
已知两个角的和是,差是,则这两个角的度数分别是 .
如图,过直线上一点作射线,,则的度数为 .
如图所示,已知,若,,,则点到的距离是 ,点到的距离是 .
已知和的两边分别互相垂直,且比的倍少,则的度数为________.
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
马小虎准备制作一个封闭的正方体盒子,他先用个大小一样的正方形制成如图所示的拼接图形,经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子从,,,,五个阴影正方形中选一个.
已知:如图,,,,求证:.
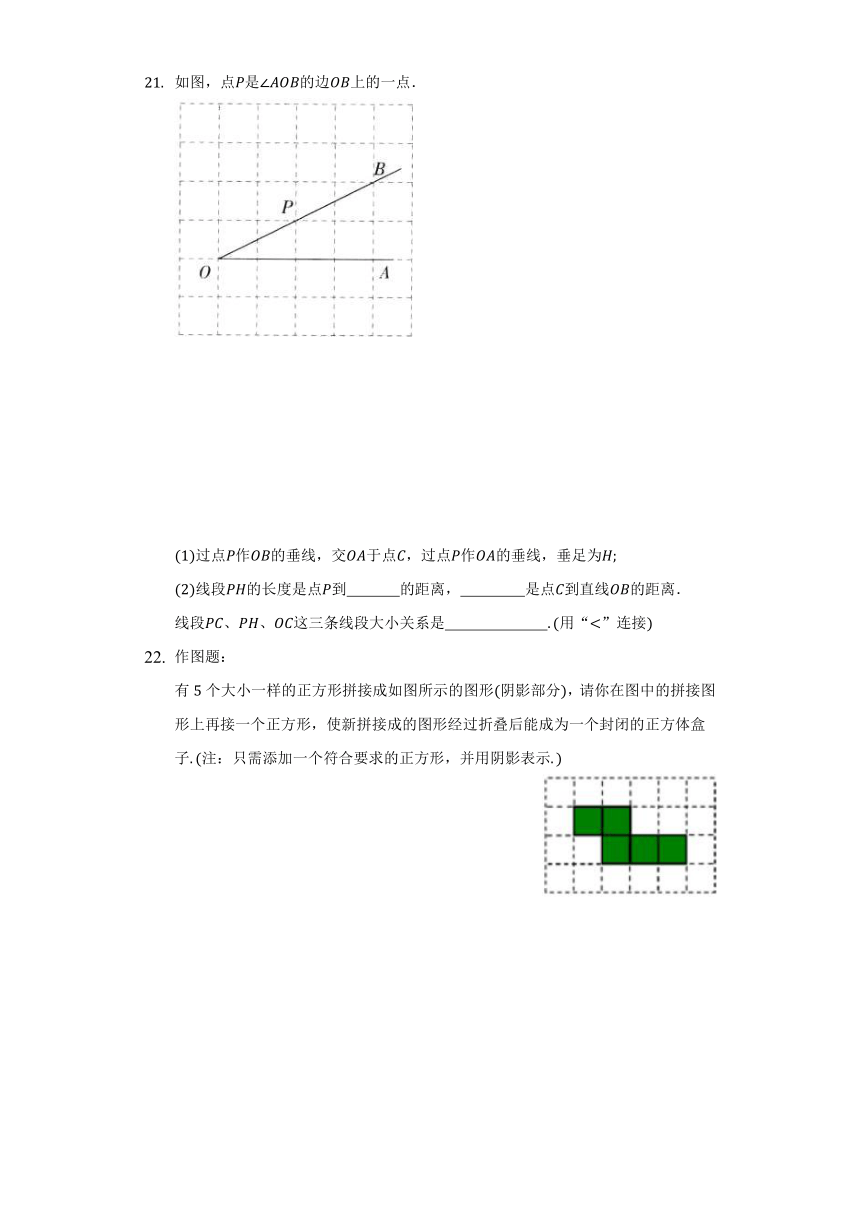
如图,点是的边上的一点.
过点作的垂线,交于点,过点作的垂线,垂足为
线段的长度是点到 的距离, 是点到直线的距离.
线段、、这三条线段大小关系是 用“”连接
作图题:
有个大小一样的正方形拼接成如图所示的图形阴影部分,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子注:只需添加一个符合要求的正方形,并用阴影表示
如图,在三角形中,,垂足为,点在上,,垂足为.
与平行吗为什么
如果,且,求的度数.
七巧板游戏是我国古代人民创造的益智游戏,现有一副七巧板如图所示.
你能在七巧板图中找出哪些你所熟悉的图形
用七巧板可以拼出许多图形,如图所示的狐狸和小桥,你知道它们各部分分别是由七巧板中的哪一块图形构成的吗请在图中标出来
你自己能设计两个由七巧板拼出的图案吗并给拼成的图案配上恰当的名字.
平面上有条直线,其中没有两条直线互相平行即每两条直线都相交,也没有三条或三条以上的直线通过同一点请问:
这条直线共有多少个交点
这条直线把平面分割为多少个区域
已知:直线分别与直线,相交于点,,并且.
如图,求证:;
如图,点在直线,之间,连接,,求证:;
如图,在的条件下,射线是的平分线,在的延长线上取点,连接,若,,求的度数.
答案和解析
1.【答案】
【解析】
【分析】
略
【解答】
对于正方体的表面展开图,相对的面之间一定相隔一个小正方形,故可以判断“你”的对面是“利”.
2.【答案】
【解析】
【分析】
略
【解答】
若两条直线平行,则一定没有交点,故A不正确
C、显然不正确故选B.
3.【答案】
【解析】
【分析】
略
【解答】
解:在同一个平面内,两条直线只有两种位置关系,即平行和相交故选D.
4.【答案】
【解析】
【分析】
略
【解答】
解:在同一平面内,两直线的位置关系有平行和相交两种,其中不相交的两条直线叫平行线,故A、、C错误,
选D.
5.【答案】
【解析】
【分析】
略
【解答】
解:过点作于,到直线的距离是指垂线段的长度,故选D.
6.【答案】
【解析】
【分析】
略
【解答】
根据立体图形的特征可得,题图中从左往右数,第个、第个、第个图形是立体图形,共个,
故选B.
7.【答案】
【解析】
【分析】
略
【解答】
由题图可知,该几何体的侧面为个三角形,底面为正方形,故该几何体为四棱锥.
故选B.
8.【答案】
【解析】
【分析】
略
【解答】
解:时”字所在面与“中”字所在面是相对面,“代”字所在面与“国”字所在面是相对面,
“新”字所在面与“梦”字所在面是相对面.
故选D.
9.【答案】
【解析】
【分析】
略
【解答】
圆柱的侧面展开图是长方形,故A选项不符合题意
三棱柱的侧面展开图是矩形,故B选项不符合题意;
圆锥的侧面展开图是扇形,故C选项符合题意
三棱锥的侧面展开图不是扇形,故D选项不符合题意.
故选C.
10.【答案】
【解析】
【分析】
略
【解答】
由长方体的展开图的特征可知选A.
11.【答案】不相交
相交
【解析】
【分析】
略
【解答】
教室里黑板的上边框和下边框所在的直线没有公共点,是不相交的,上边框和左边框所在的直线有公共点,
是相交的.
12.【答案】
【解析】
【分析】
本题主要考查角的计算,角平分线的定义,垂线的定义,根据角平分线的定义可得,由垂线的定义,可求解的度数.
【解答】
解:平分,,
,
,
,
.
故答案为.
13.【答案】
【解析】
【分析】
此题主要考查了垂线段、点到直线距离的定义.此题主要考查了垂线段、点到直线距离的定义.根据“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
根据“从直线外一点作直线的垂线,这一点与垂足之间的线段,叫做垂线段.”即可得出结论.
【解答】
解:根据垂线段、点到直线距离的定义可知,
点到直线的距离等于的长度,即为.
故答案为.
14.【答案】
【解析】
【分析】
略
【解答】
因为时针指向“”,分针指向“”,
又每小时时针转过的角度为,
所以.
15.【答案】,
【解析】
【分析】
略
【解答】
解:由题意知,这两个角中较大的角的度数为,
则较小的角的度数为.
16.【答案】
【解析】
【分析】
略
【解答】
解:,
.
17.【答案】
【解析】解:,即,
若,,,
那么到的距离是:,
到的距离是:.
故答案为:,.
直接利用点到直线的距离以及三角形面积求法分别得出答案.
此题主要考查了点到直线的距离,正确结合三角形面积求出到的距离是解题关键.
18.【答案】或
【解析】
【分析】
此题主要考查了角的计算,以及垂直的定义,关键是根据图形理清角之间的和差关系.
有两种情况:如图,根据,列方程可得结论;如图,根据,列方程可得结论.
【解答】
解:设,则,
分两种情况:
如图,
和的两边分别互相垂直,
,
即,
,
;
如图,
,,
,
,
,
,
综上所述,的度数为或,
故答案为或.
19.【答案】解:选择正方形或或或.
【解析】见答案
20.【答案】证明:如图,
,,
,
,
;
又,
,
.
【解析】本题考查了垂线的性质,平行线的性质及判定,熟记定理是正确解题的关键.
首先由,可得,根据两直线平行,同位角相等及等量代换可推出,利用内错角相等,两直线平行可得.
21.【答案】解:如图.
线段的长度是点到直线的距离,线段的长度是点到直线的距离,
线段、、这三条线段的大小关系是.
【解析】见答案
22.【答案】解:如下图所示答案不唯一
【解析】见答案
23.【答案】解:.
理由如下:
,,
,
;
,
,
,
,
,
.
【解析】本题主要考查了平行线的判定与性质,解答本题的关键是掌握利用平行线的性质求角的度数的思路与方法.
根据垂线的概念得出,再根据平行线的判定定理进行解答,即可得出结论;
根据平行线的性质得出,根据已知条件得出,根据平行线的判定定理得出,再根据平行线的性质进行解答,即可求解.
24.【答案】解:等腰直角三角形、正方形、平行四边形.
如图所示.
如图所示.
【解析】见答案
25.【答案】解:条直线有个交点条直线有个交点条直线有个交点条直线有个交点
条直线有个交点
,依此类推,条直线的交点个数为,即条直线有个交点.
条直线将平面分成个区域条直线将平面分成个区域
条直线将平面分成个区域条直线将平面分成个区域
条直线将平面分成个区域
,依此类推,条直线将平面分成的区域数为,
即条直线将平面分成个区域.
【解析】见答案
26.【答案】解:证明:如图,,.
,
;
证明:如图,过点作,
又,
.
,.
;
如图,令,,则,,
射线是的平分线,
,
,
,
,
,
过点作,则,,
,
,
,
,
,
,
.
【解析】本题考查了平行线的判定与性质,角度计算,解决本题的关键是掌握平行线的判定与性质.
根据已知条件和对顶角相等即可证明;
如图,过点作,可得进而可以证明;
如图,令,,则,,过点作,可得,,进而可得结论.
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
如图是一个正方体的表面展开图,图中的“你”的相对面是( )
A. 顺 B. 利 C. 一 D. 祝
下列说法正确的是( )
A. 两条互相平行的直线可能有交点
B. 两条直线相交,有且只有一个公共点
C. 平面内过一点可能有两条直线与已知直线垂直
D. 直线外一点与直线上各点连接的所有线段中,垂线段不一定最短
在同一平面内,两直线的位置关系必是( )
A. 相交 B. 平行 C. 垂直或平行 D. 相交或平行
下列说法中正确的是( )
A. 两条不相交的直线是平行线
B. 同一平面内,两条不相交的线段是平行线
C. 同一平面内,两条不相交的射线是平行线
D. 两条射线平行,是指它们所在的直线平行
下列图形中,线段的长表示点到直线距离的是( )
A. B.
C. D.
如图所示的图形中,立体图形的个数是( )
A. B. C. D.
如图是某个几何体的展开图,则该几何体是( )
A. 三棱锥
B. 四棱锥
C. 三棱柱
D. 四棱柱
如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“新”字的一面的相对面上的字是( )
A. 代
B. 中
C. 国
D. 梦
下列几何体中,其侧面展开图为扇形的是( )
A. B.
C. D.
如图是一个长方体纸盒,它的展开图可能是( )
A. B.
C. D.
二、填空题(本大题共8小题,共24分)
教室里黑板的上边框和下边框所在的直线是 的直线,上边框和左边框所在的直线是 的直线填“相交”或“不相交”
如图,在内部作,平分若,则 .
如图,已知,,其中,,,,那么点到的距离是________.
时,一个时钟的钟面上的时针及分针的位置如图所示,则此时分针与时针所成的的度数是 .
已知两个角的和是,差是,则这两个角的度数分别是 .
如图,过直线上一点作射线,,则的度数为 .
如图所示,已知,若,,,则点到的距离是 ,点到的距离是 .
已知和的两边分别互相垂直,且比的倍少,则的度数为________.
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
马小虎准备制作一个封闭的正方体盒子,他先用个大小一样的正方形制成如图所示的拼接图形,经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子从,,,,五个阴影正方形中选一个.
已知:如图,,,,求证:.
如图,点是的边上的一点.
过点作的垂线,交于点,过点作的垂线,垂足为
线段的长度是点到 的距离, 是点到直线的距离.
线段、、这三条线段大小关系是 用“”连接
作图题:
有个大小一样的正方形拼接成如图所示的图形阴影部分,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子注:只需添加一个符合要求的正方形,并用阴影表示
如图,在三角形中,,垂足为,点在上,,垂足为.
与平行吗为什么
如果,且,求的度数.
七巧板游戏是我国古代人民创造的益智游戏,现有一副七巧板如图所示.
你能在七巧板图中找出哪些你所熟悉的图形
用七巧板可以拼出许多图形,如图所示的狐狸和小桥,你知道它们各部分分别是由七巧板中的哪一块图形构成的吗请在图中标出来
你自己能设计两个由七巧板拼出的图案吗并给拼成的图案配上恰当的名字.
平面上有条直线,其中没有两条直线互相平行即每两条直线都相交,也没有三条或三条以上的直线通过同一点请问:
这条直线共有多少个交点
这条直线把平面分割为多少个区域
已知:直线分别与直线,相交于点,,并且.
如图,求证:;
如图,点在直线,之间,连接,,求证:;
如图,在的条件下,射线是的平分线,在的延长线上取点,连接,若,,求的度数.
答案和解析
1.【答案】
【解析】
【分析】
略
【解答】
对于正方体的表面展开图,相对的面之间一定相隔一个小正方形,故可以判断“你”的对面是“利”.
2.【答案】
【解析】
【分析】
略
【解答】
若两条直线平行,则一定没有交点,故A不正确
C、显然不正确故选B.
3.【答案】
【解析】
【分析】
略
【解答】
解:在同一个平面内,两条直线只有两种位置关系,即平行和相交故选D.
4.【答案】
【解析】
【分析】
略
【解答】
解:在同一平面内,两直线的位置关系有平行和相交两种,其中不相交的两条直线叫平行线,故A、、C错误,
选D.
5.【答案】
【解析】
【分析】
略
【解答】
解:过点作于,到直线的距离是指垂线段的长度,故选D.
6.【答案】
【解析】
【分析】
略
【解答】
根据立体图形的特征可得,题图中从左往右数,第个、第个、第个图形是立体图形,共个,
故选B.
7.【答案】
【解析】
【分析】
略
【解答】
由题图可知,该几何体的侧面为个三角形,底面为正方形,故该几何体为四棱锥.
故选B.
8.【答案】
【解析】
【分析】
略
【解答】
解:时”字所在面与“中”字所在面是相对面,“代”字所在面与“国”字所在面是相对面,
“新”字所在面与“梦”字所在面是相对面.
故选D.
9.【答案】
【解析】
【分析】
略
【解答】
圆柱的侧面展开图是长方形,故A选项不符合题意
三棱柱的侧面展开图是矩形,故B选项不符合题意;
圆锥的侧面展开图是扇形,故C选项符合题意
三棱锥的侧面展开图不是扇形,故D选项不符合题意.
故选C.
10.【答案】
【解析】
【分析】
略
【解答】
由长方体的展开图的特征可知选A.
11.【答案】不相交
相交
【解析】
【分析】
略
【解答】
教室里黑板的上边框和下边框所在的直线没有公共点,是不相交的,上边框和左边框所在的直线有公共点,
是相交的.
12.【答案】
【解析】
【分析】
本题主要考查角的计算,角平分线的定义,垂线的定义,根据角平分线的定义可得,由垂线的定义,可求解的度数.
【解答】
解:平分,,
,
,
,
.
故答案为.
13.【答案】
【解析】
【分析】
此题主要考查了垂线段、点到直线距离的定义.此题主要考查了垂线段、点到直线距离的定义.根据“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
根据“从直线外一点作直线的垂线,这一点与垂足之间的线段,叫做垂线段.”即可得出结论.
【解答】
解:根据垂线段、点到直线距离的定义可知,
点到直线的距离等于的长度,即为.
故答案为.
14.【答案】
【解析】
【分析】
略
【解答】
因为时针指向“”,分针指向“”,
又每小时时针转过的角度为,
所以.
15.【答案】,
【解析】
【分析】
略
【解答】
解:由题意知,这两个角中较大的角的度数为,
则较小的角的度数为.
16.【答案】
【解析】
【分析】
略
【解答】
解:,
.
17.【答案】
【解析】解:,即,
若,,,
那么到的距离是:,
到的距离是:.
故答案为:,.
直接利用点到直线的距离以及三角形面积求法分别得出答案.
此题主要考查了点到直线的距离,正确结合三角形面积求出到的距离是解题关键.
18.【答案】或
【解析】
【分析】
此题主要考查了角的计算,以及垂直的定义,关键是根据图形理清角之间的和差关系.
有两种情况:如图,根据,列方程可得结论;如图,根据,列方程可得结论.
【解答】
解:设,则,
分两种情况:
如图,
和的两边分别互相垂直,
,
即,
,
;
如图,
,,
,
,
,
,
综上所述,的度数为或,
故答案为或.
19.【答案】解:选择正方形或或或.
【解析】见答案
20.【答案】证明:如图,
,,
,
,
;
又,
,
.
【解析】本题考查了垂线的性质,平行线的性质及判定,熟记定理是正确解题的关键.
首先由,可得,根据两直线平行,同位角相等及等量代换可推出,利用内错角相等,两直线平行可得.
21.【答案】解:如图.
线段的长度是点到直线的距离,线段的长度是点到直线的距离,
线段、、这三条线段的大小关系是.
【解析】见答案
22.【答案】解:如下图所示答案不唯一
【解析】见答案
23.【答案】解:.
理由如下:
,,
,
;
,
,
,
,
,
.
【解析】本题主要考查了平行线的判定与性质,解答本题的关键是掌握利用平行线的性质求角的度数的思路与方法.
根据垂线的概念得出,再根据平行线的判定定理进行解答,即可得出结论;
根据平行线的性质得出,根据已知条件得出,根据平行线的判定定理得出,再根据平行线的性质进行解答,即可求解.
24.【答案】解:等腰直角三角形、正方形、平行四边形.
如图所示.
如图所示.
【解析】见答案
25.【答案】解:条直线有个交点条直线有个交点条直线有个交点条直线有个交点
条直线有个交点
,依此类推,条直线的交点个数为,即条直线有个交点.
条直线将平面分成个区域条直线将平面分成个区域
条直线将平面分成个区域条直线将平面分成个区域
条直线将平面分成个区域
,依此类推,条直线将平面分成的区域数为,
即条直线将平面分成个区域.
【解析】见答案
26.【答案】解:证明:如图,,.
,
;
证明:如图,过点作,
又,
.
,.
;
如图,令,,则,,
射线是的平分线,
,
,
,
,
,
过点作,则,,
,
,
,
,
,
,
.
【解析】本题考查了平行线的判定与性质,角度计算,解决本题的关键是掌握平行线的判定与性质.
根据已知条件和对顶角相等即可证明;
如图,过点作,可得进而可以证明;
如图,令,,则,,过点作,可得,,进而可得结论.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
