第19章 二次函数与反比例函数 单元测试卷(Word版,含解析)
文档属性
| 名称 | 第19章 二次函数与反比例函数 单元测试卷(Word版,含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 00:00:00 | ||
图片预览



文档简介
第19章 二次函数与反比例函数 单元测试卷
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
下列关于二次函数的说法正确的是( )
A. 它的图象经过点 B. 它的图象的对称轴是直线
C. 当时,随的增大而减小 D. 当时,有最大值为
函数,,中,图象开口大小的顺序是( )
A. B. C. D.
当函数的函数值随着的增大而减小时,的取值范围是( )
A. B. C. D. 为任意实数
如图,是反比例函数图象上一点,且矩形的面积为,则反比例函数的表达式是( )
A. B.
C. 或 D.
抛物线的对称轴是直线( )
A. B. C. D.
观察函数的图象,则下列判断正确的是( )
A. 若,互为相反数,则与的函数值相等
B. 对于同一个自变量,有两个函数值与它对应
C. 对任意一个实数,都有两个和它对应
D. 对任意实数,都有
如果二次函数的值恒大于,那么必有( )
A. ,取任意实数 B. ,
C. , D. ,均可取任意实数
下列函数中,当时,随的增大而减小的是( )
A. B. C. D.
抛物线经过点,且对称轴为直线,其部分图象如图所示对于此抛物线有如下四个结论:若,则当时的函数值小于时的函数值.
其中正确结论的序号是( )
A. B. C. D.
如图,在同一平面直角坐标系中,函数与的图象可能是( )
A. B.
C. D.
二、填空题(本大题共8小题,共24分)
抛物线,,的共同性质是 写出一条即可
若函数是关于的反比例函数,则的值为 .
已知函数满足下列两个条件:当时,随的增大而减小它的图象经过坐标原点请写出一个符合上述条件的函数的表达式 .
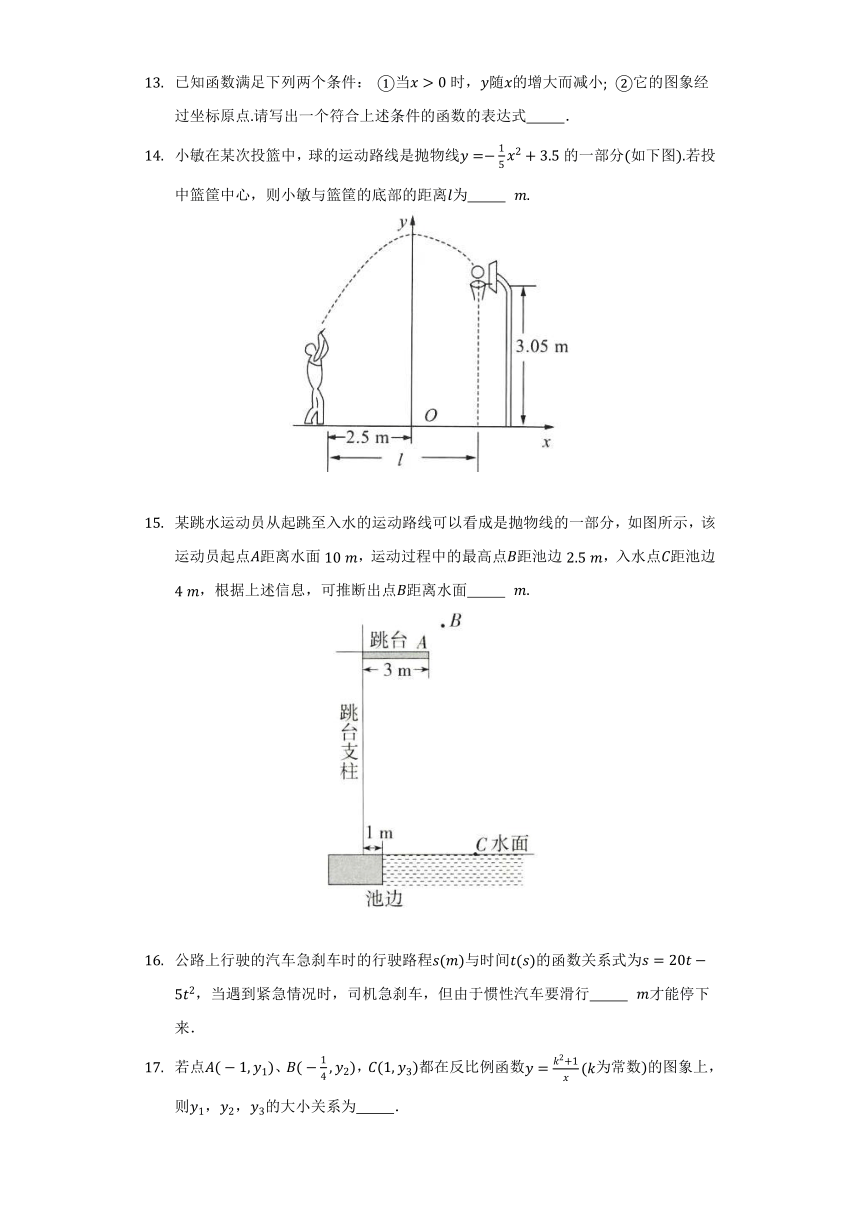
小敏在某次投篮中,球的运动路线是抛物线的一部分如下图若投中篮筐中心,则小敏与篮筐的底部的距离为
某跳水运动员从起跳至入水的运动路线可以看成是抛物线的一部分,如图所示,该运动员起点距离水面,运动过程中的最高点距池边,入水点距池边,根据上述信息,可推断出点距离水面
公路上行驶的汽车急刹车时的行驶路程与时间的函数关系式为,当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行 才能停下来.
若点、,都在反比例函数为常数的图象上,则,,的大小关系为 .
如图,正方形的顶点和正方形的顶点都在函数的图象上,若正方形的面积为,则点的坐标为 .
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
已知函数.
在什么条件下,函数的图象分布在第一、第三象限?在什么条件下,函数的图象分布在第二、第四象限?
在什么条件下,随的增大而减小?在什么条件下,随的增大而增大?
写出下列二次函数图象的开口方向、对称轴和顶点坐标.
.
分别根据下列条件,求二次函数的表达式.
图象过点,和;
图象过点和,对称轴为;
图象过点,当时有最大值.
如图,人工喷泉有一个竖直的喷水枪,喷水口距地面,喷出水流的轨迹是抛物线如果水流的最高点到喷水枪所在直线的距离为,且水流的落地点距离喷水枪底部的距离为,那么,水流的最高点距离地面是多少米?
已知二次函数的图象经过,,三点,回答下列问题:
自变量在什么范围内变化时,因变量随自变量的增大而减小?
函数有最大值,还是有最小值?自变量取什么值时,因变量取得这个最大值或最小值?最大值或最小值是多少?
这个图象经过怎样的平移运动,就能得到以原点为顶点的一条抛物线?
在同一直角坐标系中,分别画出抛物线与抛物线的图象,并根据图象求出这两个函数图象的交点,这两个交点有什么关系
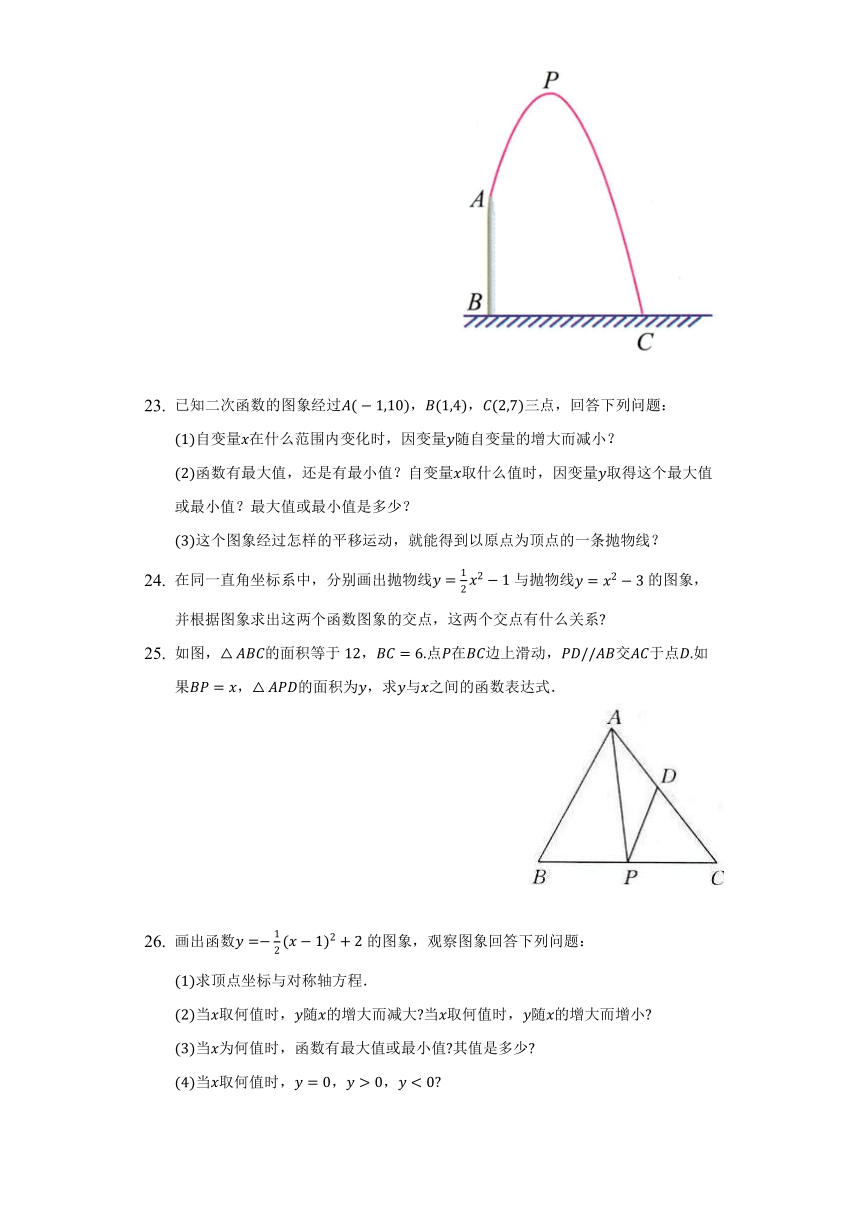
如图,的面积等于,点在边上滑动,交于点如果,的面积为,求与之间的函数表达式.
画出函数的图象,观察图象回答下列问题:
求顶点坐标与对称轴方程.
当取何值时,随的增大而减大当取何值时,随的增大而增小
当为何值时,函数有最大值或最小值其值是多少
当取何值时,,,
答案和解析
1.【答案】
【解析】
【分析】
略
【解答】
略
2.【答案】
【解析】
【分析】
略
【解答】
略
3.【答案】
【解析】
【分析】
略
【解答】
略
4.【答案】
【解析】
【分析】
略
【解答】
略
5.【答案】
【解析】
【分析】
略
【解答】
略
6.【答案】
【解析】
【分析】
略
【解答】
略
7.【答案】
【解析】
【分析】
略
【解答】
略
8.【答案】
【解析】
【分析】
略
【解答】
略
9.【答案】
【解析】
【分析】
略
【解答】
略
10.【答案】
【解析】
【分析】
略
【解答】
略
11.【答案】对称轴都是轴或顶点都是原点
【解析】
【分析】
略
【解答】
形如的函数图象的对称轴是轴,顶点是.
12.【答案】
【解析】
【分析】
略
【解答】
解:函数是关于的反比例函数,
,解得.
13.【答案】答案不唯一,如
【解析】
【分析】
略
【解答】
略
14.【答案】
【解析】
【分析】
略
【解答】
略
15.【答案】
【解析】
【分析】
略
【解答】
解:如图,以水面所在的直线为轴,以跳台支柱所在的直线为轴建立直角坐标系,
由题意得,,对称轴为直线,
设表达式为,
把,代入,得解得
所以,
所以,故点距离水面.
16.【答案】
【解析】
【分析】
略
【解答】
解:,
当时,有最大值,为.
故由于惯性汽车要滑行才能停下来.
17.【答案】
【解析】
【分析】
略
【解答】
解:,该函数图象位于第一、三象限,在每个象限内,随的增大而减小,
点、,都在反比例函数为常数的图象上,
,,,
故答案为.
18.【答案】
【解析】
【分析】
略
【解答】
解:正方形的面积为,
正方形的边长为,
正方形的顶点在反比例函数的图象上,
点坐标为,,
设正方形的边长为,,
正方形的顶点在反比例函数的图象上,
将代入反比例函数得,解得,
又,.
点的坐标为
19.【答案】; ;.
【解析】见答案.
20.【答案】开口向下,对称轴是,顶点坐标为.
开口向上,对称轴是,顶点坐标为.
开口向上,对称轴是,顶点坐标为.
【解析】见答案.
21.【答案】二次函数的表达式为.
二次函数的表达式为.
二次函数的表达式为.
【解析】见答案.
22.【答案】水流的最高点距离地面 .
【解析】见答案.
23.【答案】时,因变量随自变量的增大而减小.
函数有最小值,当时,因变量取最小值.
将这个图象向左平移个单位长度,再向下平移个单位长度或先向下平移个单位长度,
再向左平移个单位长度,就能得到以原点为顶点的一条抛物线.
【解析】见答案.
24.【答案】解:如图所示:
两个交点为,,它们关于轴对称.
【解析】见答案
25.【答案】解:作于点,作于点图略.
,,
,.
,.
.
,
即.
【解析】见答案
26.【答案】解:顶点坐标,对称轴方程;
当时,随的增大而增大当时,随的增大而减小;
当时,函数有最大值,最大值是;
当或时,当或时,当时,.
【解析】见答案
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
下列关于二次函数的说法正确的是( )
A. 它的图象经过点 B. 它的图象的对称轴是直线
C. 当时,随的增大而减小 D. 当时,有最大值为
函数,,中,图象开口大小的顺序是( )
A. B. C. D.
当函数的函数值随着的增大而减小时,的取值范围是( )
A. B. C. D. 为任意实数
如图,是反比例函数图象上一点,且矩形的面积为,则反比例函数的表达式是( )
A. B.
C. 或 D.
抛物线的对称轴是直线( )
A. B. C. D.
观察函数的图象,则下列判断正确的是( )
A. 若,互为相反数,则与的函数值相等
B. 对于同一个自变量,有两个函数值与它对应
C. 对任意一个实数,都有两个和它对应
D. 对任意实数,都有
如果二次函数的值恒大于,那么必有( )
A. ,取任意实数 B. ,
C. , D. ,均可取任意实数
下列函数中,当时,随的增大而减小的是( )
A. B. C. D.
抛物线经过点,且对称轴为直线,其部分图象如图所示对于此抛物线有如下四个结论:若,则当时的函数值小于时的函数值.
其中正确结论的序号是( )
A. B. C. D.
如图,在同一平面直角坐标系中,函数与的图象可能是( )
A. B.
C. D.
二、填空题(本大题共8小题,共24分)
抛物线,,的共同性质是 写出一条即可
若函数是关于的反比例函数,则的值为 .
已知函数满足下列两个条件:当时,随的增大而减小它的图象经过坐标原点请写出一个符合上述条件的函数的表达式 .
小敏在某次投篮中,球的运动路线是抛物线的一部分如下图若投中篮筐中心,则小敏与篮筐的底部的距离为
某跳水运动员从起跳至入水的运动路线可以看成是抛物线的一部分,如图所示,该运动员起点距离水面,运动过程中的最高点距池边,入水点距池边,根据上述信息,可推断出点距离水面
公路上行驶的汽车急刹车时的行驶路程与时间的函数关系式为,当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行 才能停下来.
若点、,都在反比例函数为常数的图象上,则,,的大小关系为 .
如图,正方形的顶点和正方形的顶点都在函数的图象上,若正方形的面积为,则点的坐标为 .
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
已知函数.
在什么条件下,函数的图象分布在第一、第三象限?在什么条件下,函数的图象分布在第二、第四象限?
在什么条件下,随的增大而减小?在什么条件下,随的增大而增大?
写出下列二次函数图象的开口方向、对称轴和顶点坐标.
.
分别根据下列条件,求二次函数的表达式.
图象过点,和;
图象过点和,对称轴为;
图象过点,当时有最大值.
如图,人工喷泉有一个竖直的喷水枪,喷水口距地面,喷出水流的轨迹是抛物线如果水流的最高点到喷水枪所在直线的距离为,且水流的落地点距离喷水枪底部的距离为,那么,水流的最高点距离地面是多少米?
已知二次函数的图象经过,,三点,回答下列问题:
自变量在什么范围内变化时,因变量随自变量的增大而减小?
函数有最大值,还是有最小值?自变量取什么值时,因变量取得这个最大值或最小值?最大值或最小值是多少?
这个图象经过怎样的平移运动,就能得到以原点为顶点的一条抛物线?
在同一直角坐标系中,分别画出抛物线与抛物线的图象,并根据图象求出这两个函数图象的交点,这两个交点有什么关系
如图,的面积等于,点在边上滑动,交于点如果,的面积为,求与之间的函数表达式.
画出函数的图象,观察图象回答下列问题:
求顶点坐标与对称轴方程.
当取何值时,随的增大而减大当取何值时,随的增大而增小
当为何值时,函数有最大值或最小值其值是多少
当取何值时,,,
答案和解析
1.【答案】
【解析】
【分析】
略
【解答】
略
2.【答案】
【解析】
【分析】
略
【解答】
略
3.【答案】
【解析】
【分析】
略
【解答】
略
4.【答案】
【解析】
【分析】
略
【解答】
略
5.【答案】
【解析】
【分析】
略
【解答】
略
6.【答案】
【解析】
【分析】
略
【解答】
略
7.【答案】
【解析】
【分析】
略
【解答】
略
8.【答案】
【解析】
【分析】
略
【解答】
略
9.【答案】
【解析】
【分析】
略
【解答】
略
10.【答案】
【解析】
【分析】
略
【解答】
略
11.【答案】对称轴都是轴或顶点都是原点
【解析】
【分析】
略
【解答】
形如的函数图象的对称轴是轴,顶点是.
12.【答案】
【解析】
【分析】
略
【解答】
解:函数是关于的反比例函数,
,解得.
13.【答案】答案不唯一,如
【解析】
【分析】
略
【解答】
略
14.【答案】
【解析】
【分析】
略
【解答】
略
15.【答案】
【解析】
【分析】
略
【解答】
解:如图,以水面所在的直线为轴,以跳台支柱所在的直线为轴建立直角坐标系,
由题意得,,对称轴为直线,
设表达式为,
把,代入,得解得
所以,
所以,故点距离水面.
16.【答案】
【解析】
【分析】
略
【解答】
解:,
当时,有最大值,为.
故由于惯性汽车要滑行才能停下来.
17.【答案】
【解析】
【分析】
略
【解答】
解:,该函数图象位于第一、三象限,在每个象限内,随的增大而减小,
点、,都在反比例函数为常数的图象上,
,,,
故答案为.
18.【答案】
【解析】
【分析】
略
【解答】
解:正方形的面积为,
正方形的边长为,
正方形的顶点在反比例函数的图象上,
点坐标为,,
设正方形的边长为,,
正方形的顶点在反比例函数的图象上,
将代入反比例函数得,解得,
又,.
点的坐标为
19.【答案】; ;.
【解析】见答案.
20.【答案】开口向下,对称轴是,顶点坐标为.
开口向上,对称轴是,顶点坐标为.
开口向上,对称轴是,顶点坐标为.
【解析】见答案.
21.【答案】二次函数的表达式为.
二次函数的表达式为.
二次函数的表达式为.
【解析】见答案.
22.【答案】水流的最高点距离地面 .
【解析】见答案.
23.【答案】时,因变量随自变量的增大而减小.
函数有最小值,当时,因变量取最小值.
将这个图象向左平移个单位长度,再向下平移个单位长度或先向下平移个单位长度,
再向左平移个单位长度,就能得到以原点为顶点的一条抛物线.
【解析】见答案.
24.【答案】解:如图所示:
两个交点为,,它们关于轴对称.
【解析】见答案
25.【答案】解:作于点,作于点图略.
,,
,.
,.
.
,
即.
【解析】见答案
26.【答案】解:顶点坐标,对称轴方程;
当时,随的增大而增大当时,随的增大而减小;
当时,函数有最大值,最大值是;
当或时,当或时,当时,.
【解析】见答案
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
