第20章 解直角三角形 单元测试卷(Word版,含答案)
文档属性
| 名称 | 第20章 解直角三角形 单元测试卷(Word版,含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 670.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 00:00:00 | ||
图片预览

文档简介
第20章 解直角三角形 单元测试卷
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
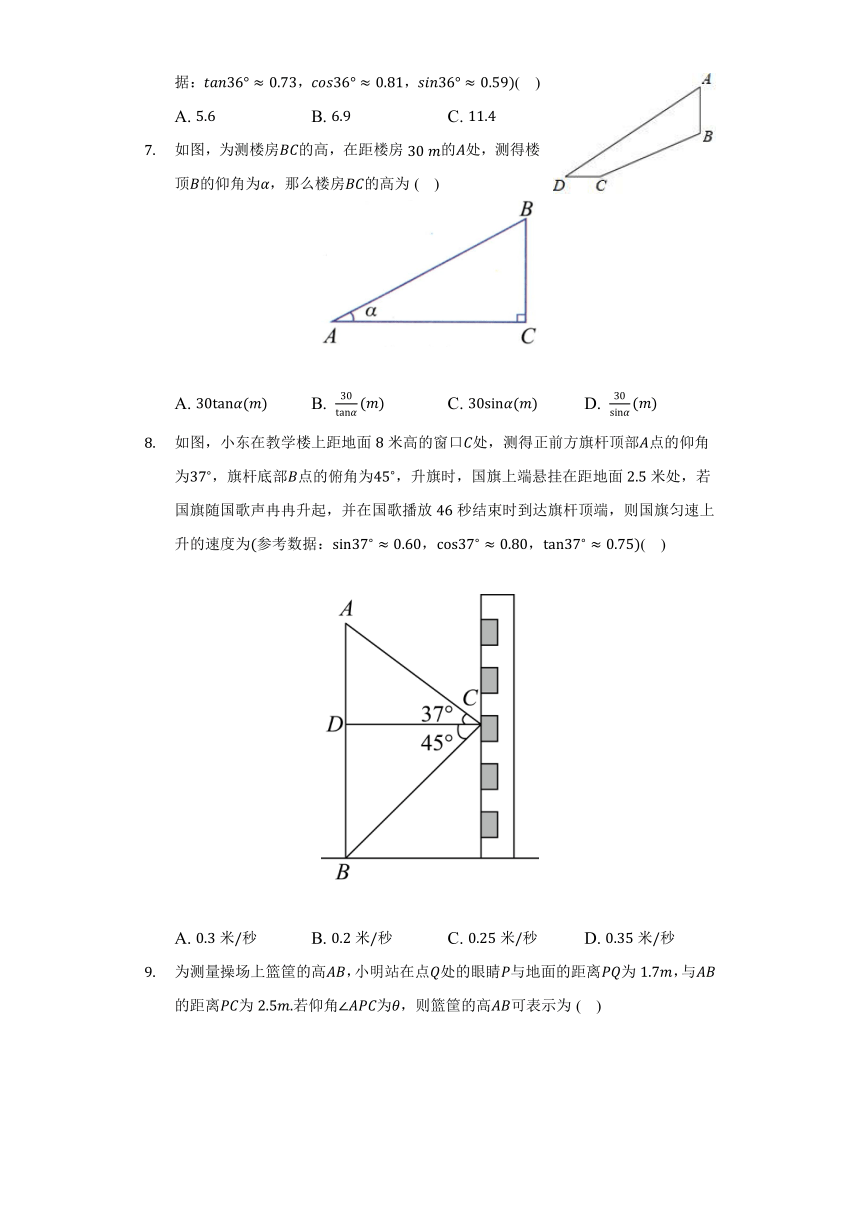
河堤的横断面如图所示,堤高为,迎水坡的长是,那么斜坡的坡度是( )
A. B. C. D.
在中,,,那么的值等于( )
A. B. C. D.
已知为锐角,且,则的度数为( )
A. B. C. D.
如图所示,河堤横断面迎水坡的坡比是,堤高,则坡面的长度是( )
A. B.
C. D.
如图,在中,,,,则下列三角函数表示正确的是( )
A. B.
C. D.
某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯自由上下选择项目难度.其中斜坡轨道的坡度或坡比为:,米,米,,其中点、、、均在同一平面内则垂直升降电梯的高度约为米.精确到米,参考数据:,,( )
A. B. C. D.
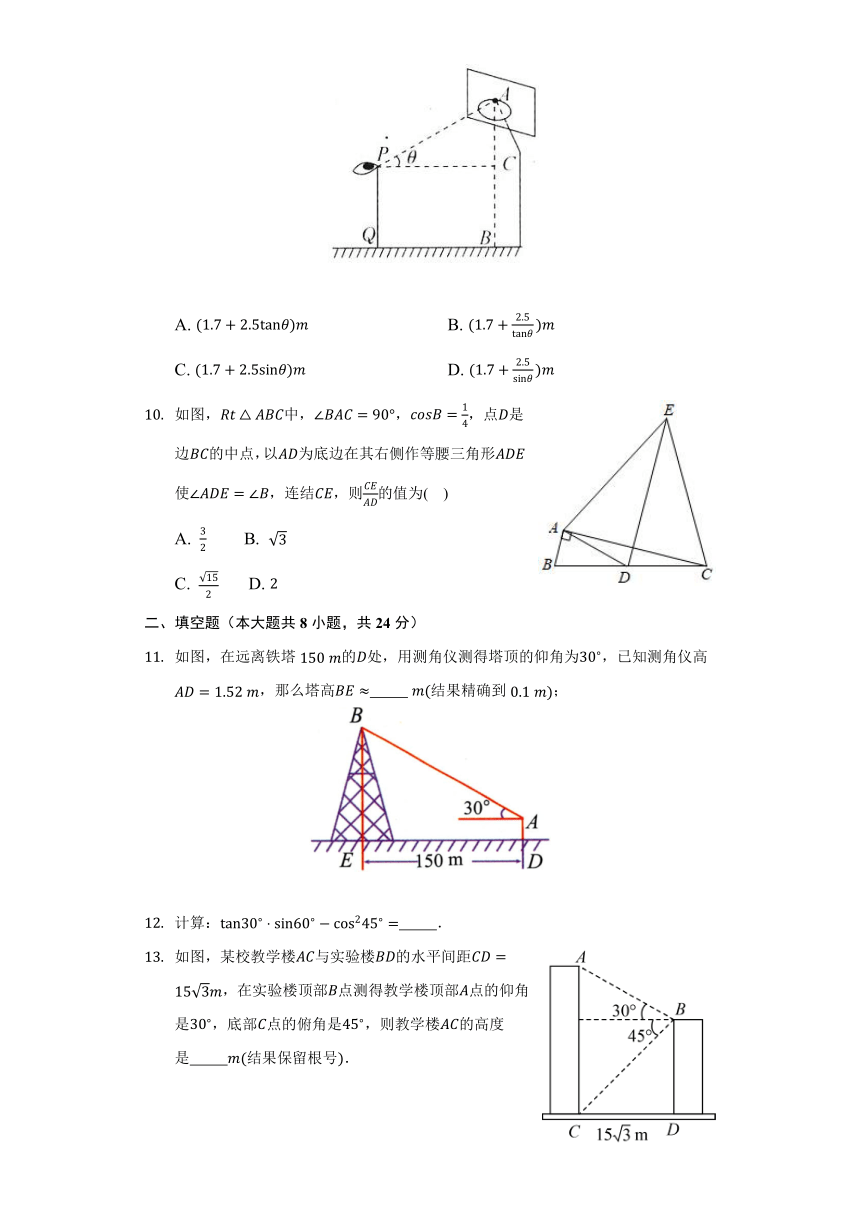
如图,为测楼房的高,在距楼房的处,测得楼顶的仰角为,那么楼房的高为( )
A. B. C. D.
如图,小东在教学楼上距地面米高的窗口处,测得正前方旗杆顶部点的仰角为,旗杆底部点的俯角为,升旗时,国旗上端悬挂在距地面米处,若国旗随国歌声冉冉升起,并在国歌播放秒结束时到达旗杆顶端,则国旗匀速上升的速度为参考数据:,,( )
A. 米秒 B. 米秒 C. 米秒 D. 米秒
为测量操场上篮筐的高,小明站在点处的眼睛与地面的距离为,与的距离为若仰角为,则篮筐的高可表示为( )
A. B.
C. D.
如图,中,,,点是边的中点,以为底边在其右侧作等腰三角形,使,连结,则的值为( )
A. B.
C. D.
二、填空题(本大题共8小题,共24分)
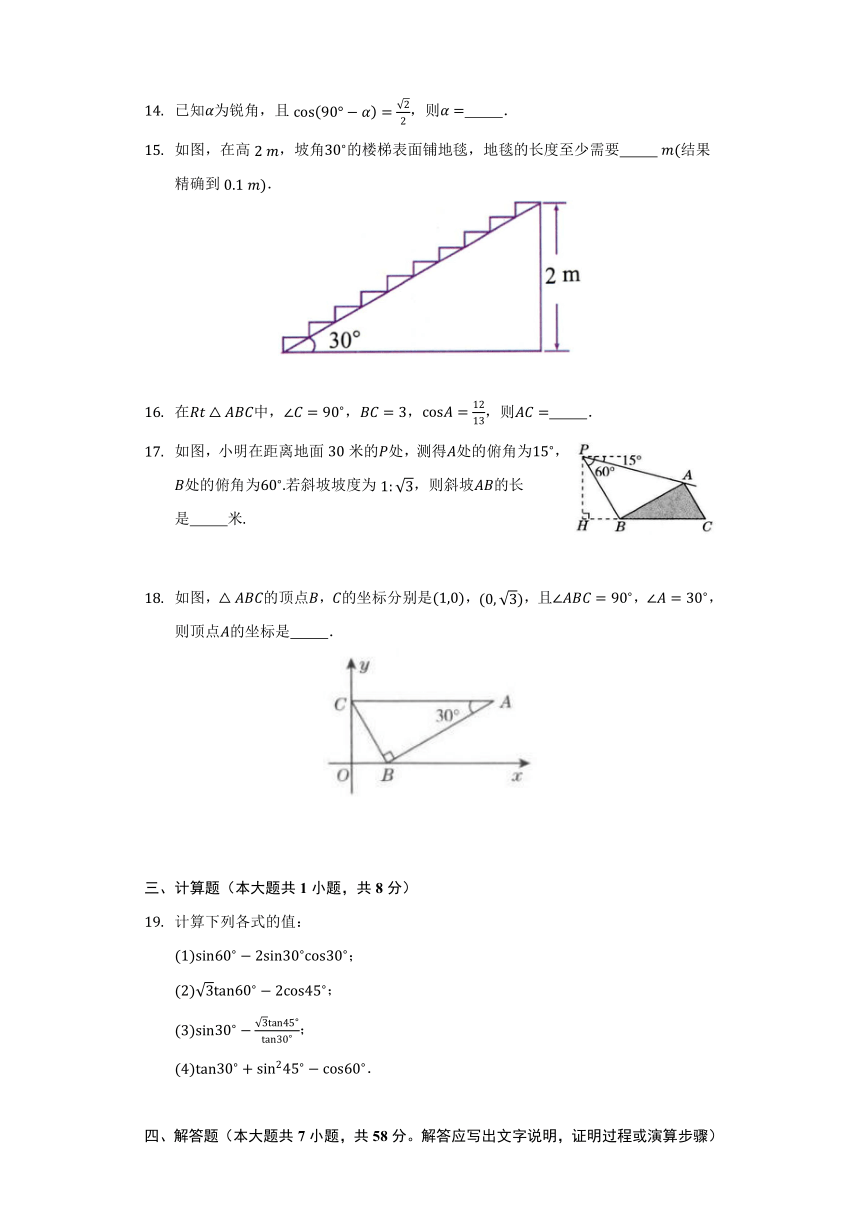
如图,在远离铁塔的处,用测角仪测得塔顶的仰角为,已知测角仪高,那么塔高 结果精确到;
计算: .
如图,某校教学楼与实验楼的水平间距,在实验楼顶部点测得教学楼顶部点的仰角是,底部点的俯角是,则教学楼的高度是 结果保留根号.
已知为锐角,且,则 .
如图,在高,坡角的楼梯表面铺地毯,地毯的长度至少需要 结果精确到.
在中,,,,则 .
如图,小明在距离地面米的处,测得处的俯角为,处的俯角为若斜坡坡度为,则斜坡的长是 米
如图,的顶点,的坐标分别是,,且,,则顶点的坐标是 .
三、计算题(本大题共1小题,共8分)
计算下列各式的值:
;
;
;
.
四、解答题(本大题共7小题,共58分。解答应写出文字说明,证明过程或演算步骤)
本小题分
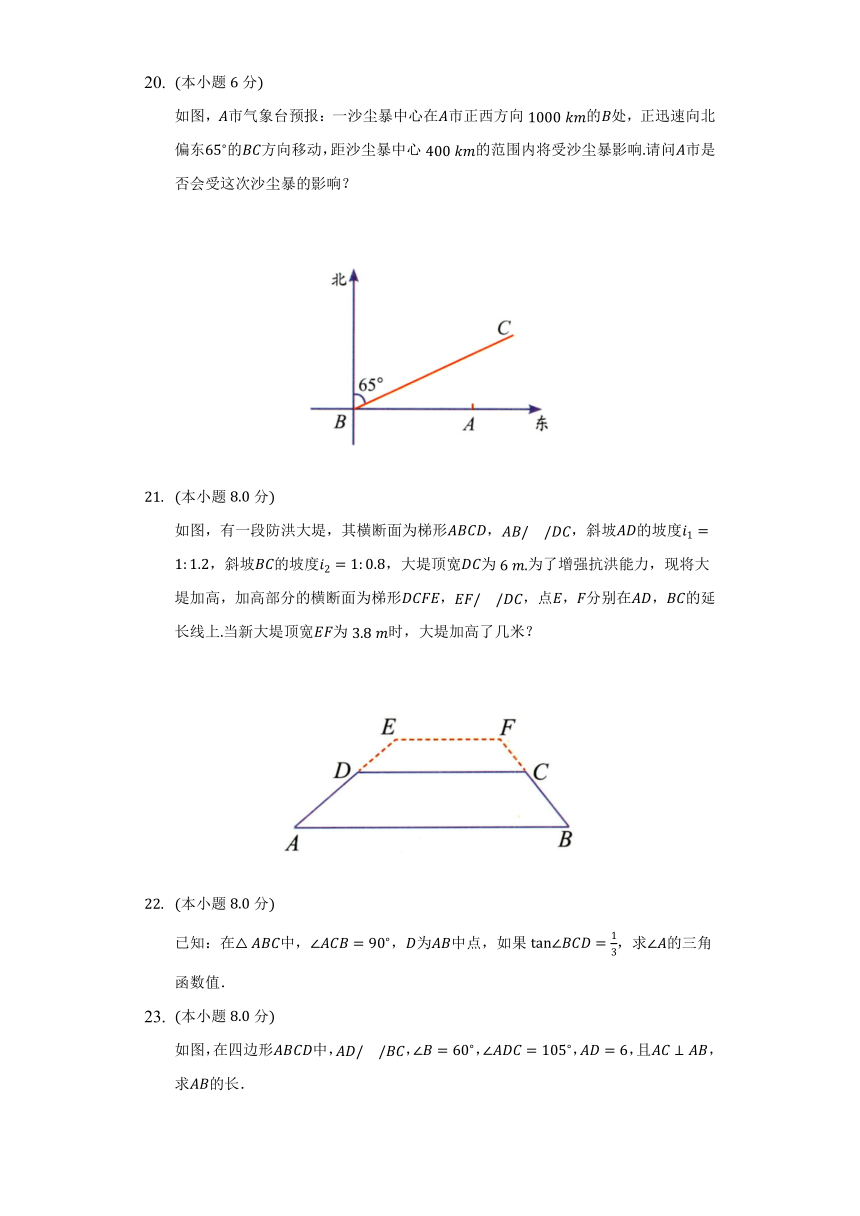
如图,市气象台预报:一沙尘暴中心在市正西方向的处,正迅速向北偏东的方向移动,距沙尘暴中心的范围内将受沙尘暴影响请问市是否会受这次沙尘暴的影响?
本小题分
如图,有一段防洪大堤,其横断面为梯形,,斜坡的坡度,斜坡的坡度,大堤顶宽为为了增强抗洪能力,现将大堤加高,加高部分的横断面为梯形,,点,分别在,的延长线上当新大堤顶宽为时,大堤加高了几米?
本小题分
已知:在中,,为中点,如果,求的三角函数值.
本小题分
如图,在四边形中,,,,,且,求的长.
本小题分
在数学活动课上,老师带领学生去测量位于良乡的昊天塔的高度如图,在处用高米的测角仪测得塔顶的仰角为,向塔的方向前进米到达处,在处测得塔顶的仰角为,求昊天塔的高约为多少米结果精确到米,,
本小题分
如图,一艘海轮位于灯塔的南偏东方向,距离灯塔海里的处,它计划沿正北方向航行,去往位于灯塔的北偏东方向上的处.
问处距离灯塔有多远结果精确到海里
假设有一圆形暗礁区域,它的圆心位于射线上,距离灯塔海里的点处圆形暗礁区域的半径为海里,进入这个区域,就有触礁的危险.
请判断海轮到达处是否有触礁的危险,并说明理由
如果海轮从处继续向正北方向航行,是否有触礁的危险直接写出结论,不用说明理由.
参考数据:,
本小题分
图是自动卸货汽车卸货时的状态图,图是其示意图汽车的车厢采用液压机构,车厢的支撑顶杆的底部支撑点在水平线的下方,与水平线之间的夹角是,卸货时,车厢与水平线成,此时与支撑顶杆的夹角为,若米,求的长度结果保留一位小数参考数据:,,,,,,
答案和解析
1.【答案】
【解析】
【分析】
略
【解答】
略
2.【答案】
【解析】
【分析】
略
【解答】
略
3.【答案】
【解析】略
4.【答案】
【解析】略
5.【答案】
【解析】略
6.【答案】
【解析】
【分析】
本题考查了解直角三角形的应用,利用勾股定理得出,的长是解题关键,又利用了正切函数,线段的和差.
根据勾股定理,可得,的长,根据正切函数,可得的长,再根据线段的和差,可得答案.
【解答】
解:如图
,
由斜坡轨道的坡度或坡比为:,得
::.
设,.
在中,由勾股定理,得
,
即,
解得,
,,
,
由,得
,
解得.
由线段的和差,得
,
故选:.
7.【答案】
【解析】
【分析】
略
【解答】
略
8.【答案】
【解析】
【分析】
略
【解答】
解:由题意得,在中,米,,
是等腰直角三角形,
米,
在中,米,,
米,
旗杆的高为米.
升旗时,国旗上升的高度是米,
国旗匀速上升的速度为米秒,故选C.
9.【答案】
【解析】略
10.【答案】
【解析】解:设交于,过点作于.
,,
,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
故选:.
设交于,过点作于首先证明,再证明,可得结论.
本题考查解直角三角形,等腰三角形的判定和性质,平行线的判定与性质,解题的关键是证明,属于中考常考题型.
11.【答案】
【解析】
【分析】
略
【解答】
略
12.【答案】
【解析】
【分析】
略
【解答】
解:原式.
13.【答案】
【解析】略
14.【答案】
【解析】略
15.【答案】
【解析】
【分析】
略
【解答】
略
16.【答案】
【解析】
【分析】
略
【解答】
在中,,,
不妨设,则,
由勾股定理得,,即,
所以,所以,
故答案为.
17.【答案】
【解析】如图,过点作于点,
斜坡坡度为,
,
,
在处进行观测,测得处的俯角为,处的俯角为,
,,
,
,,
,
米,,
米,
米
18.【答案】
【解析】解:过点作轴,垂足为点,如图.
,的坐标分别是,,
,.
.
,,
.
,,
.
,.
,.
,.
.
顶点的坐标是
故答案为
19.【答案】 .
【解析】见答案.
20.【答案】市不会受这次沙尘暴的影响.
【解析】见答案.
21.【答案】大堤加高了.
【解析】见答案.
22.【答案】,,.
【解析】见答案.
23.【答案】解:如图,过点作于点,则,
,.
,.
,,
在中,,,.
,.
在中,.
.
在中,,
.
【解析】见答案
24.【答案】解:如图,过作于,则米,
设米,在中,,
,
米,
在中,,
,
米,
,解得.
米,则米.
答:昊天塔的高约为米.
【解析】见答案
25.【答案】解:如图,过点作于点.
依题意可知,海里,,,
,
海里,
在中,,
海里海里.
答:处距离灯塔约海里.
海轮到达处没有触礁的危险.
理由:
如图,依题意知海里,由知海里,
海里海里海里,
海轮到达处没有触礁的危险.
如图,过点作,交的延长线于点,则,
,
海里海里,
海轮从处继续向正北方向航行,有触礁的危险.
【解析】见答案.
26.【答案】解法一:如图所示,过点作于点,
,
在中,,
米.
在中,,
米,
答:所求的长度约为米.
解法二:如图所示,过点作于点,
,
在中,,
在中,,
即米.
,即米.
又在中,,.
米.
答:所求的长度约为米.
【解析】见答案
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
河堤的横断面如图所示,堤高为,迎水坡的长是,那么斜坡的坡度是( )
A. B. C. D.
在中,,,那么的值等于( )
A. B. C. D.
已知为锐角,且,则的度数为( )
A. B. C. D.
如图所示,河堤横断面迎水坡的坡比是,堤高,则坡面的长度是( )
A. B.
C. D.
如图,在中,,,,则下列三角函数表示正确的是( )
A. B.
C. D.
某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯自由上下选择项目难度.其中斜坡轨道的坡度或坡比为:,米,米,,其中点、、、均在同一平面内则垂直升降电梯的高度约为米.精确到米,参考数据:,,( )
A. B. C. D.
如图,为测楼房的高,在距楼房的处,测得楼顶的仰角为,那么楼房的高为( )
A. B. C. D.
如图,小东在教学楼上距地面米高的窗口处,测得正前方旗杆顶部点的仰角为,旗杆底部点的俯角为,升旗时,国旗上端悬挂在距地面米处,若国旗随国歌声冉冉升起,并在国歌播放秒结束时到达旗杆顶端,则国旗匀速上升的速度为参考数据:,,( )
A. 米秒 B. 米秒 C. 米秒 D. 米秒
为测量操场上篮筐的高,小明站在点处的眼睛与地面的距离为,与的距离为若仰角为,则篮筐的高可表示为( )
A. B.
C. D.
如图,中,,,点是边的中点,以为底边在其右侧作等腰三角形,使,连结,则的值为( )
A. B.
C. D.
二、填空题(本大题共8小题,共24分)
如图,在远离铁塔的处,用测角仪测得塔顶的仰角为,已知测角仪高,那么塔高 结果精确到;
计算: .
如图,某校教学楼与实验楼的水平间距,在实验楼顶部点测得教学楼顶部点的仰角是,底部点的俯角是,则教学楼的高度是 结果保留根号.
已知为锐角,且,则 .
如图,在高,坡角的楼梯表面铺地毯,地毯的长度至少需要 结果精确到.
在中,,,,则 .
如图,小明在距离地面米的处,测得处的俯角为,处的俯角为若斜坡坡度为,则斜坡的长是 米
如图,的顶点,的坐标分别是,,且,,则顶点的坐标是 .
三、计算题(本大题共1小题,共8分)
计算下列各式的值:
;
;
;
.
四、解答题(本大题共7小题,共58分。解答应写出文字说明,证明过程或演算步骤)
本小题分
如图,市气象台预报:一沙尘暴中心在市正西方向的处,正迅速向北偏东的方向移动,距沙尘暴中心的范围内将受沙尘暴影响请问市是否会受这次沙尘暴的影响?
本小题分
如图,有一段防洪大堤,其横断面为梯形,,斜坡的坡度,斜坡的坡度,大堤顶宽为为了增强抗洪能力,现将大堤加高,加高部分的横断面为梯形,,点,分别在,的延长线上当新大堤顶宽为时,大堤加高了几米?
本小题分
已知:在中,,为中点,如果,求的三角函数值.
本小题分
如图,在四边形中,,,,,且,求的长.
本小题分
在数学活动课上,老师带领学生去测量位于良乡的昊天塔的高度如图,在处用高米的测角仪测得塔顶的仰角为,向塔的方向前进米到达处,在处测得塔顶的仰角为,求昊天塔的高约为多少米结果精确到米,,
本小题分
如图,一艘海轮位于灯塔的南偏东方向,距离灯塔海里的处,它计划沿正北方向航行,去往位于灯塔的北偏东方向上的处.
问处距离灯塔有多远结果精确到海里
假设有一圆形暗礁区域,它的圆心位于射线上,距离灯塔海里的点处圆形暗礁区域的半径为海里,进入这个区域,就有触礁的危险.
请判断海轮到达处是否有触礁的危险,并说明理由
如果海轮从处继续向正北方向航行,是否有触礁的危险直接写出结论,不用说明理由.
参考数据:,
本小题分
图是自动卸货汽车卸货时的状态图,图是其示意图汽车的车厢采用液压机构,车厢的支撑顶杆的底部支撑点在水平线的下方,与水平线之间的夹角是,卸货时,车厢与水平线成,此时与支撑顶杆的夹角为,若米,求的长度结果保留一位小数参考数据:,,,,,,
答案和解析
1.【答案】
【解析】
【分析】
略
【解答】
略
2.【答案】
【解析】
【分析】
略
【解答】
略
3.【答案】
【解析】略
4.【答案】
【解析】略
5.【答案】
【解析】略
6.【答案】
【解析】
【分析】
本题考查了解直角三角形的应用,利用勾股定理得出,的长是解题关键,又利用了正切函数,线段的和差.
根据勾股定理,可得,的长,根据正切函数,可得的长,再根据线段的和差,可得答案.
【解答】
解:如图
,
由斜坡轨道的坡度或坡比为:,得
::.
设,.
在中,由勾股定理,得
,
即,
解得,
,,
,
由,得
,
解得.
由线段的和差,得
,
故选:.
7.【答案】
【解析】
【分析】
略
【解答】
略
8.【答案】
【解析】
【分析】
略
【解答】
解:由题意得,在中,米,,
是等腰直角三角形,
米,
在中,米,,
米,
旗杆的高为米.
升旗时,国旗上升的高度是米,
国旗匀速上升的速度为米秒,故选C.
9.【答案】
【解析】略
10.【答案】
【解析】解:设交于,过点作于.
,,
,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
故选:.
设交于,过点作于首先证明,再证明,可得结论.
本题考查解直角三角形,等腰三角形的判定和性质,平行线的判定与性质,解题的关键是证明,属于中考常考题型.
11.【答案】
【解析】
【分析】
略
【解答】
略
12.【答案】
【解析】
【分析】
略
【解答】
解:原式.
13.【答案】
【解析】略
14.【答案】
【解析】略
15.【答案】
【解析】
【分析】
略
【解答】
略
16.【答案】
【解析】
【分析】
略
【解答】
在中,,,
不妨设,则,
由勾股定理得,,即,
所以,所以,
故答案为.
17.【答案】
【解析】如图,过点作于点,
斜坡坡度为,
,
,
在处进行观测,测得处的俯角为,处的俯角为,
,,
,
,,
,
米,,
米,
米
18.【答案】
【解析】解:过点作轴,垂足为点,如图.
,的坐标分别是,,
,.
.
,,
.
,,
.
,.
,.
,.
.
顶点的坐标是
故答案为
19.【答案】 .
【解析】见答案.
20.【答案】市不会受这次沙尘暴的影响.
【解析】见答案.
21.【答案】大堤加高了.
【解析】见答案.
22.【答案】,,.
【解析】见答案.
23.【答案】解:如图,过点作于点,则,
,.
,.
,,
在中,,,.
,.
在中,.
.
在中,,
.
【解析】见答案
24.【答案】解:如图,过作于,则米,
设米,在中,,
,
米,
在中,,
,
米,
,解得.
米,则米.
答:昊天塔的高约为米.
【解析】见答案
25.【答案】解:如图,过点作于点.
依题意可知,海里,,,
,
海里,
在中,,
海里海里.
答:处距离灯塔约海里.
海轮到达处没有触礁的危险.
理由:
如图,依题意知海里,由知海里,
海里海里海里,
海轮到达处没有触礁的危险.
如图,过点作,交的延长线于点,则,
,
海里海里,
海轮从处继续向正北方向航行,有触礁的危险.
【解析】见答案.
26.【答案】解法一:如图所示,过点作于点,
,
在中,,
米.
在中,,
米,
答:所求的长度约为米.
解法二:如图所示,过点作于点,
,
在中,,
在中,,
即米.
,即米.
又在中,,.
米.
答:所求的长度约为米.
【解析】见答案
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
