小升初分班考冲刺特训卷(试题)-小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 小升初分班考冲刺特训卷(试题)-小学数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 19:38:43 | ||
图片预览




文档简介
小升初分班考冲刺特训卷(试题)-小学数学六年级下册苏教版
一、选择题
1.一种盐水,盐与水的比是1:5,如果再向其中加入含盐20%的盐水若干,那么含盐率将( )
A.不变
B.下降了
C.升高了
D.无法确定
2.我们发现一些数有一个有趣的特点,一个数所有因数(除了它本身)的和等于它本身。比如6的因数有1,2,3,6,这几个因数之间的关系是:。像6这样的数叫做完全数(也叫完美数)。那么下面的数中也有这样的特点是( )。
A.12 B.28 C.32
3.将化为小数,则小数点后面第2018位上的数字是( )。
A.8 B.7 C.4 D.5
4.公交车从甲站到乙站每间隔5分钟开出一辆,全程走15分钟,某人骑自行车从乙站往甲站,开始时恰好遇见一辆公交车, 骑行过程中又遇见12辆,到甲站时又一公交车刚要出发,则这人从乙站到甲站骑行的时间是( )。
A.35分钟 B.40分钟 C.45 分钟 D.50分钟
5.将一个底面半径是3分米,高是2分米的圆柱体橡皮泥捏成与它等底等高的圆锥,能捏出( )个。
A.6 B.3 C.2 D.1
6.今年北京冬奥会的召开举世瞩目。下面描述的量中成正比例关系的是( )。
A.比赛当天的场馆温度与参赛运动员的比赛成绩
B.冬奥会已完赛项目数和未完赛项目数
C.“北京→张家口”的高铁列车,行驶的速度与时间
D.同一型号“冰墩墩”玩偶,购买的数量和总价
7.如下图,点M在点O北偏东40°方向,那么点M在点P的( )方向.
A.北偏东50° B.北偏西40° C.北偏西50°
8.如图所示,平行四边形ABCD中,AB=10厘米,BC=20厘米,BC边上的高是8厘米。EF是AD和BC的平行线,图中阴影部分的面积是( )平方厘米。
A.40 B.80 C.100 D.160
二、填空题
9.据宿迁市统计局2021年5月25日发布信息,至2020年11月1日零时,宿迁市全市常住人口为4986192人,横线上这个数读作:________,省略“万”后面的尾数是________。
10.15÷ =0.75==3∶ = 折。
11.在下面的括号里填上合适的数或单位。
(1)一桶纯净水大约18________;
(2)一个西瓜重约3________;
(3)6.08公顷=________平方米;
(4)25秒=________分。
12.一根绳长米,将它对折3次,每一段是绳长的,每段长 米。
13.________米比30米长,20千克比________千克重25%。
14.学校买来9个足球,每个a元,又买来b个篮球,每个56元。一共用去________元,一个篮球比一个足球贵________元。
15.看图数轴写数:
如图数轴上,点A表示的数是________,数轴上点C到0的距离与点B到0的距离相等,且B、C两点不重合,那么点C表示的数是________。
16.五(1)班几位同学的座位位置用数对表示如下:周明(1,3),孙芳(2,2),赵雪(4,3),王艳(3,4),李小冬(2,1)。由此可知,________坐在同行,________和________在同一列。
17.m,n都是非零自然数,若m=n,那么m,n的最大公因数是________,最小公倍数是________。
18.一根长60厘米的铁丝,正好可以围成长8厘米,宽4厘米,高________厘米的长方体框架;如果可以正好围成正方体框架,正方体框架的棱长是________厘米。
三、口算和估算
19.直接写出得数。
2.4×5= 0.36÷0.4= 25.2-4.8-5.2=
四、脱式计算
20.怎样简便就怎样算。
76×20-828÷4
21.解方程。
1.1x+0.4=9.2
五、解答题
22.在图中,甲、乙都是正方形,边长分别为 10 厘米和 12 厘米,则阴影部分的面积是多少平方厘米?
23.学校开展大课间活动,五(1)班有的学生参加了跳绳活动,25%的同学参加乒乓球活动,剩下的15人全部踢足球,五(1)班共有多少人?
24.一个圆柱的侧面展开是正方形,这个圆柱的高是6.28厘米,它的表面积和体积分别是多少?(得数保留两位小数)
25.东渡服装厂计划全年要生产6000件西装,前3个月完成了20%,照这样计算,全年任务能按时完成吗?(列式计算来说明)
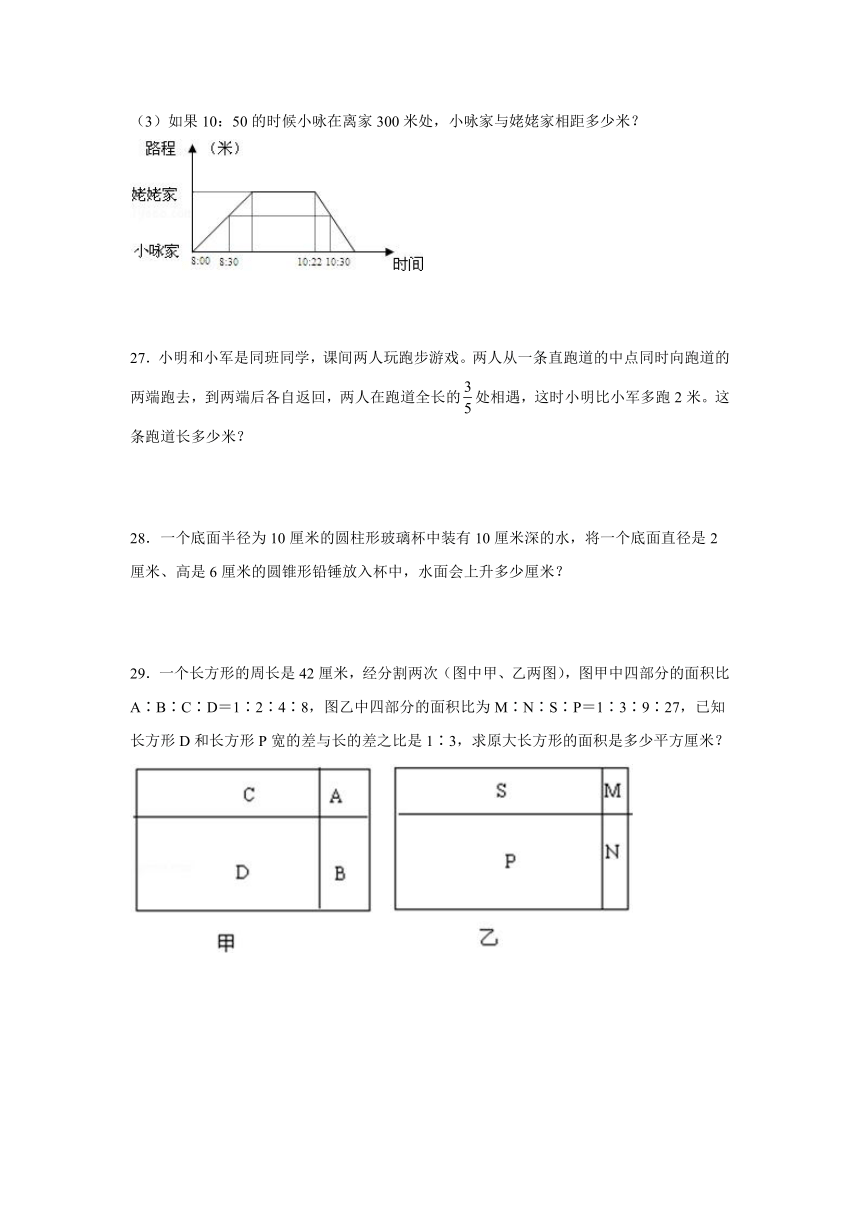
26.小咏星期日上午8:00从家骑车到姥姥家,走的线路如图。已知去时与返回的速度比是4∶5。
(1)小咏什么时候到达姥姥家?
(2)小咏在姥姥家玩了多长时间?
(3)如果10:50的时候小咏在离家300米处,小咏家与姥姥家相距多少米?
27.小明和小军是同班同学,课间两人玩跑步游戏。两人从一条直跑道的中点同时向跑道的两端跑去,到两端后各自返回,两人在跑道全长的处相遇,这时小明比小军多跑2米。这条跑道长多少米?
28.一个底面半径为10厘米的圆柱形玻璃杯中装有10厘米深的水,将一个底面直径是2厘米、高是6厘米的圆锥形铅锤放入杯中,水面会上升多少厘米?
29.一个长方形的周长是42厘米,经分割两次(图中甲、乙两图),图甲中四部分的面积比A∶B∶C∶D=1∶2∶4∶8,图乙中四部分的面积比为M∶N∶S∶P=1∶3∶9∶27,已知长方形D和长方形P宽的差与长的差之比是1∶3,求原大长方形的面积是多少平方厘米?
试卷第1页,共3页
参考答案:
1.C
【分析】根据题中盐和水的比是1:5,假设原来盐水中盐有1份,则水有5份,则配成后的盐水有(5+1)份,进而根据计算公式为:含盐率=×100%,求出原来盐水的含盐率,这时只要把后来加入的盐水的含盐率和原来盐水的含盐率进行比较,看后来加入的盐水的含盐率比原来盐水浓度大还是小,就能知道盐水的含盐率是提高了,还是降低了。
【详解】原来盐水的含盐率:×100%≈16.7%, 因为后来加入的盐水的含盐率是20%,20%>16.7%,
所以含盐率将升高;
故答案为:C
【点睛】本题的关键是求出原来盐水的含盐率。
2.B
【分析】根据完全数的特点,先分别求出各个选项的因数,再逐项分析即可。
【详解】A.12的因数有1、2、3、4、6、12,1+2+3+4+6=16,不是完全数;
B.28的因数有1、2、4、7、14、28,1+2+4+7+14=28,是完全数;
C.32的因数有1、2、4、8、16、32,1+2+4+8+16=31,不是完全数。
故答案为:B
【点睛】本题主要考查学生对于完全数的理解及运用。
3.C
【分析】化为小数是0.142857142857…,小数点后面以142857六个数字为一周期,用2018除以6,看余数是几,就从一周期中数到第几,就是第2018位上的数字。
【详解】=0.142857142857…
2018÷6=336……2
第2018位上的数字是4。
故答案为:C
【点睛】本题考查周期问题,明确题目中的周期规律是解题的关键。
4.D
【分析】公交车每5分钟开出一辆,全程15分钟,15÷5=3辆,当自行车出发时正好有一辆公交车到达乙站,即这时有一公交车刚要从甲站出发,路上还有3-1=2辆公交车(后出发的一辆刚离站5分钟),途中自行车共遇见12辆公交,也就是说在自行车出发后又有12-2=10辆公交车从甲站出发(自行车出发后第10辆出站的公交车刚离开甲站5分钟),所以总共用时是10×5=50分钟,据此解答。
【详解】[12-(15÷5-1)]×5
=[12-(3-1)]×5
=[12-2]×5
=10×5
=50(分钟)
故答案为:D
【点睛】此题考查的是行程问题,解题时注意发车间隔。
5.B
【分析】根据“等底等高的圆柱是圆锥体积的3倍”可知,将一个底面半径是3分米,高是2分米的圆柱体橡皮泥捏成与它等底等高的圆锥,能捏出3个。
【详解】根据分析可知,
将一个底面半径是3分米,高是2分米的圆柱体橡皮泥捏成与它等底等高的圆锥,能捏出3个。
故答案为:B
【点睛】此题考查了等底等高的圆柱与圆锥的体积的关系的灵活应用。
6.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定 ,还是对应的乘积定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A.比赛当天的场馆温度与参赛运动员的比赛成绩没有一定的关系,所以不成比例;
B.冬奥会已完赛项目数和未完赛项目数的和一定,所以,冬奥会已完赛项目数和未完赛项目数不成比例;
C.速度×时间=路程(一定),所以,“北京→张家口”的高铁列车,行驶的速度与时间成反比例关系;
D.总价÷数量=单价(一定),所以,同一型号“冰墩墩”玩偶,购买的数量和总价成正比例。
故答案为:D
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
7.C
【详解】略
8.B
【分析】因为EF是AD和BC的平行线,所以四边形BCFE和EFDA都是平行四边形,两个平行四边形中阴影部分的面积和空白处的面积相等,所以总的阴影部分的面积等于平行四边形ABCD面积的一半;据此求解即可。
【详解】根据分析可得:阴影部分的面积等于平行四边形ABCD面积的一半。
20×8÷2
=160÷2
=80(平方厘米)
所以,阴影部分的面积是80平方厘米。
故答案为:B
【点睛】本题主要考查了组合图形的面积,解题的关键是把不规则图形转化为规则图形。
9. 四百九十八万六千一百九十二 499万
【分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零,即可读出此数;
省略“万”后面的尾数,就是四舍五入到万位,就是把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字,据此解答。
【详解】4986192读作:四百九十八万六千一百九十二
4986192≈499万
【点睛】本题考查了整数的读法和求近似数,注意求近似数时要带计数单位。
10.20;9;4;七五
【分析】把0.75化成分数并化简是,根据分数的基本性质,分子、分母都乘3就是;根据分数与除法的关系,=3÷4,再根据商不变的性质被除数、除数都乘5就是15÷20;根据比与分数的关系,=3∶4;把0.75的小数点向右移动两位添上百分号就是75%,根据折扣的意义,75%就是七五折。
【详解】15÷20=0.75==3∶4=七五折
【点睛】此题主要是考查除法、小数、分数、百分数、比、折扣之间的关系及转化。利用它们之间的关系和性质进行转化即可。
11.(1)升##L
(2)千克##kg
(3)60800
(4)
【分析】(1)(2)根据体积单位和质量单位的认识和数据的大小,结合实际经验进行解答;
(3)1公顷=10000平方米,高级单位换算成低级单位,乘进率,据此解答;
(4)1分=60秒,低级单位换算成高级单位,除以进率,据此解答。
(1)
一桶纯净水大约18升;
(2)
一个西瓜重约3千克;
(3)
6.08公顷=60800平方米
(4)
25秒=分
【点睛】根据体积、质量单位和数据大小的认识,结合实际经验以及熟记进率是解答本题的关键。
12.;0.1
【分析】把这根绳子的长度看作单位“1”,将它对折3次,被平均分成(2×2×2)段,即8段,求每段占全长的几分之几,用1除以8;求每段长,用这根绳子的长度除以8。
【详解】2×2×2=8(段)
1÷8=
÷8=0.1(米)
所以每一段是绳长的,每段长0.1米。
【点睛】解决此题关键一是弄清这根绳子对折3次被平均分成的段数,二是弄清求的是“分率”还是“具体的数量”。求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量。注意:分率不能带单位名称,而具体的数量要带单位名称。
13. 36 16
【分析】把30米看作单位“1”,用单位“1”加上,可以计算出所求的长度是30米的几分之几,再根据一个数乘分数的意义,求出未知的长度;把未知的质量看作单位“1”,用单位“1”加上25%可以计算出20千克是未知质量的百分之几,再根据分数除法的意义,求出未知的质量。
【详解】30×(1+)
=30×
=36(米)
20÷(1+25%)
=20÷1.25
=16(千克)
【点睛】本题考查分数应用题的解题方法,解题关键是先找出题目中的单位“1”是哪个量,再根据分数乘法的意义与分数除法的意义,列式计算。
14. 9a+56b 56-a
【分析】(1)根据单价×数量=总价,分别求出学校买来9个足球和b个篮球花的钱数,再加起来就是一共用去的钱数;
(2)用篮球的单价减去足球的单价,就是一个篮球比一个足球贵的钱数。
【详解】(1)a×9+56×b=(9a+56b)元
(2)(56-a)元
【点睛】关键是把给出的字母当作已知数,再根据基本的数量关系解决问题;注意字母与数相乘时要简写,即省略乘号,把数写在字母的前面。
15. 0.6## ﹣1.7##﹣1##﹣
【分析】把数轴上一个单位长度平均分成5份,每份表示0.2,点A表示其中3份,即0.6;把数轴上一个单位长度平均分成10份,每份表示0.1,点B表示这样的17份,即1.7。在数轴上到原点的距离相等,且不重合的点,不考虑性质符号时,数值完全相同,但是在原点左边表示负数,前面加“﹣”,在圆点右表示正数,前面加“﹢”(或省略)。
【详解】如图:
点A表示的数是0.6,数轴上点C到0的距离与点B到0的距离相等,且B、C两点不重合,那么点C表示的数是﹣1.7。
【点睛】数轴是规定了原点(0点)、方向和单位长度的直线,在原点(0点)左边的点所表示的数都是负数,右边的点表示的数都是正数。不看性质符号,数值相同的两个数,是过原点垂线对称的对称点。
16. 周明和赵雪 孙芳 李小冬
【分析】数对的第一个数表示列,第二个数表示行,据此即可解答。
【详解】周明(1,3),表示坐在第1列,第3行;
孙芳(2,2),表示坐在第2列,第2行;
赵雪(4,3),表示坐在第4列,第3行;
王艳(3,4),表示坐在第3列,第4行;
李小冬(2,1),表示坐在第2列,第1行;
此可知,周明和赵雪坐在同一行,孙芳和李小冬在同一列。
【点睛】本题主要考查学生对数对与位置关系的掌握和灵活运用。
17. m n
【分析】两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数。
【详解】因为m,n都是非零自然数,m=n,所以,m÷n=,n÷m=3,所以m,n的最大公因数是m,最小公倍数是n。
【点睛】熟练掌握为倍数关系的两个数的最大公因数是较小的数,最小公倍数是较大的数,是解答此题的关键。
18. 3 5
【分析】根据长方体棱长总和公式:棱长总和=(长+宽+高)×4;高=棱长总和÷4-长-宽;代入数据即可求出长方体的高;长方体棱长总和等于正方体棱长总和,根据正方体棱长总和公式:棱长总和=棱长×12,棱长=棱长总和÷12,代入数据,即可解答。
【详解】60÷4-8-4
=15-8-4
=7-4
=3(厘米)
60÷12=5(厘米)
【点睛】利用长方体特征和正方体特征以及长方体棱长总和公式、正方体棱长总和公式进行解答,关键是熟记公式,灵活运用。
19.12;0.9;;15.2;
9;;0.008;1
【详解】略
20.1313;8;;
;;
【分析】第一小题,先分别计算乘法与除法,再计算减法;
第二小题,利用加法交换律和加法结合律,把原式变为:,即可简算;
第三小题, 先算括号里面的加法,再算括号外面的除法,最后计算括号外面的乘法;
第四小题,利用乘法分配律,把原式变为:,可以简算;
第五小题,先算小括号里面的加法,再算中括号里面的减法,最后计算中括号外面的除法;
第六小题,先把原式化简为:,再利用乘法分配律把原式变为:,可以简算。
【详解】76×20-828÷4
=1520-207
=1313
=
=7+1
=8
=
=
=
=
=
=1-
=
=
=
=
=
=
=
=
=1×
=
21.x=8;;x=
【分析】第一小题,根据等式的性质,方程的两边先同时减去0.4,再同时除以1.1;即可解方程。
第二小题,先化简原式为:,再根据等式性质2,方程的两边同时除以;即可解题。
第三小题,根据比例的基本性质,把原式转化成7x=5×0.4,再根据等式的性质2,两边同时除以7,即可解题。
【详解】1.1x+0.4=9.2
解:1.1x+0.4-0.4=9.2-0.4
1.1x=8.8
1.1x÷1.1=8.8÷1.1
x=8
解:
解:7x=5×0.4
7x÷7=2÷7
x=
22.113.04平方厘米
【分析】由题意可知:阴影部分的面积=梯形ABOC的面积+以12厘米为半径的圆的面积的-三角形ABD的面积,据此解答即可。
【详解】(10+12)×10÷2+3.14×122÷4﹣10×(10+12)÷2
=110+113.04-110
=113.04(平方厘米)
答:阴影部分的面积是113.04平方厘米。
【点睛】解决此题的关键是把阴影部分分成常见的平面图形的和与差,进一步求得面积。
23.36人
【分析】本题的单位“1”是五(1)班的总学生人数;设五(1)班的人数为x,那么五(1)班参加了跳绳活动的人数是x,参加乒乓球活动的人数是25%x,余下的人数就是15人。五(1)班的人数减去参加了跳绳活动的x人减去参加乒乓球活动的25%x人就是踢足球的人数15人;根据这个等量关系列出方程。
【详解】解:五(1)班共有x人。由题意可得:
x-x-25%x=15
x-x=15
x-x=15
x=15
x=36
答:五(1)班共有36人。
【点睛】本题也可用算术法:根据“的学生参加了跳绳活动,25%的同学参加乒乓球活动,剩下的15人全部踢足球”,找到15人占五(1)人数的(1--25%);因此:15÷(1--25%)=36(人)。
24.45.72平方厘米;19.72立方厘米
【分析】根据“圆柱的侧面展开图是一个正方形”可知,圆柱的高就是圆柱的底面周长,根据底面周长求出底面的半径,再根据圆柱的表面积和体积公式来进行计算。
【详解】6.28÷3.14÷2=1(厘米)
3.14×12×2+6.28×6.28
=3.14×1×2+39.4384
=6.28+39.4384
=45.7184
≈45.72(平方厘米)
3.14×12×6.28
=3.14×1×6.28
=19.7192
≈19.72(立方厘米)
答:它的表面积约是45.72平方厘米、体积约是19.72立方厘米。
【点睛】这题是考查学生对圆柱表面积和体积的掌握情况,要知道圆柱的表面积计算方法:;明确圆柱的体积计算公式: ;本题解题的关键是求出圆柱底面的半径。
25.不能
【分析】前3个月完成了20%,每个月就完成全部任务的(20%÷3),照这样计算,剩下的(12-3)个月能完成计划的百分之几,再同剩下的百分之几比较即可。
【详解】一年有12个月,
(12-3)×(20%÷3)
=9×
=60%
1-20%=80%
80%>60%
答:全年任务不能按时完成。
【点睛】本题中的生产西装的总数可不用,可把西装的.总数看作间作单位“1” 来进行解答,这样较简便。
26.(1)8时40分 ;
(2)1小时50分;
(3)2400米
【分析】(1)要求小咏什么时候到达姥姥家,必须求出从家到姥姥家用的时间,由“已知去时与返回的速度比是4∶5”可知,去的时间与返回的时间的比是5∶4,观察图可知,同一段路返回的时间是用了10时30分-10时22分=8分钟,所以去的那同一段路用了8÷4×5=10分钟,所以到姥姥家的时间是:8:30+00:10=8:40。
(2)用10:22减去8:40得到的差就是他在姥姥家玩的时间。
(3)我们找出行驶300米的路程所用的时间是多少,然后求出去时的速度,再乘以去时的时间,就是小咏家与姥姥家路程。
【详解】(1)(10时30分-10时22分)÷4×5
=8÷4×5
=10(分钟)
8时30分+10分=8时40分
答:小咏8时40分到达姥姥家。
(2)10时30分-8时40分=1小时50分
答:小咏在姥姥家玩了1小时50分。
(3)10时22分+(8时40分-8时00)÷5×4
=10:22+00:32
=10时:54分
300÷(10时54分-10时50分)××(8时40分-8时00)
=75××40
=60×40
=2400(米)
答:如果10:50的时候小咏在离家300米处,小咏家与姥姥家相距2400米。
【点睛】本题运用时间的推算及行程问题的有关知识进行解答即可。
27.10米
【分析】两人从一条直跑道的中点同时向跑道的两端跑去,到两端后各自返回时,两人各跑了全程的,当两人在跑道全长的处相遇时,小明应该跑了全程的(+),小军应跑了全程的:+(1-),求出小明比小军多跑的距离也就是2米占的分率,依据分数除法意义即可解答。
【详解】1-=
2÷
=2÷
=2÷
=10(米)
答:这条跑道长10米。
【点睛】解答本题的关键是求出2米占这条跑道的分率。
28.0.02厘米
【分析】因圆锥形铅锤的高小于玻璃杯内水的高度,所以铅锤能全部浸没在水中,根据圆锥的体积公式求出铅锤的体积,再除以玻璃杯的底面积,就是水面上升的高度。
【详解】×3.14×(2÷2)2×6÷(3.14×102)
=×3.14×12×6÷(3.14×100)
=×3.14×1×6÷314
=6.28÷314
=0.02(厘米)
答:水面会上升0.02厘米。
【点睛】本题主要考查了学生对圆锥和圆柱体积公式的掌握,熟记:圆柱的体积计算公式: 、圆锥的体积公式:,是解答此题的关键。
29.90平方厘米
【分析】因为长方形的周长为42厘米,则长方形的长与宽的和为21厘米;因为B和D的面积比为2∶8,则D的面积:(B+D)的面积=8∶(2+8)=4∶5,因为D与下面的B和D合起来组成的长方形的宽相等,则长的比就等于面积之比,则D的长:原长方形的长=4∶5,即D的长=原长方形的长×,同理,根据D的面积:(C+D)的面积=8∶(4+8)=2∶3,得出:D的宽=原长方形的宽×;P的长=原长方形的长×,P的宽=原长方形的宽×,设出原长方形的长与宽,再根据长方形D和长方形P宽的差与长的差之比是1∶3,列方程解答出原长方形的长与宽,再根据面积公式计算即可。
【详解】解:设原长方形的长为x,宽为y,则x+y=21
由面积的比例关系知,
D的长为x,宽为y
P的长为x,宽为y
(y-y)∶(x-x)=1∶3
(y-y)×3=(x-x)×1
y-2y=x
y=x
x∶y=∶
x∶y=5∶2
x=
代入x+y=21得:
+y=21
y=21
y=6
则x=6×=15
所以原长方形的面积为:15×6=90(平方厘米)
答:原大长方形的面积是90平方厘米。
【点睛】解决本题的关键是根据面积比求出D和P的长与宽和原长方形的长与宽的关系,再根据题中数量关系列方解答。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.一种盐水,盐与水的比是1:5,如果再向其中加入含盐20%的盐水若干,那么含盐率将( )
A.不变
B.下降了
C.升高了
D.无法确定
2.我们发现一些数有一个有趣的特点,一个数所有因数(除了它本身)的和等于它本身。比如6的因数有1,2,3,6,这几个因数之间的关系是:。像6这样的数叫做完全数(也叫完美数)。那么下面的数中也有这样的特点是( )。
A.12 B.28 C.32
3.将化为小数,则小数点后面第2018位上的数字是( )。
A.8 B.7 C.4 D.5
4.公交车从甲站到乙站每间隔5分钟开出一辆,全程走15分钟,某人骑自行车从乙站往甲站,开始时恰好遇见一辆公交车, 骑行过程中又遇见12辆,到甲站时又一公交车刚要出发,则这人从乙站到甲站骑行的时间是( )。
A.35分钟 B.40分钟 C.45 分钟 D.50分钟
5.将一个底面半径是3分米,高是2分米的圆柱体橡皮泥捏成与它等底等高的圆锥,能捏出( )个。
A.6 B.3 C.2 D.1
6.今年北京冬奥会的召开举世瞩目。下面描述的量中成正比例关系的是( )。
A.比赛当天的场馆温度与参赛运动员的比赛成绩
B.冬奥会已完赛项目数和未完赛项目数
C.“北京→张家口”的高铁列车,行驶的速度与时间
D.同一型号“冰墩墩”玩偶,购买的数量和总价
7.如下图,点M在点O北偏东40°方向,那么点M在点P的( )方向.
A.北偏东50° B.北偏西40° C.北偏西50°
8.如图所示,平行四边形ABCD中,AB=10厘米,BC=20厘米,BC边上的高是8厘米。EF是AD和BC的平行线,图中阴影部分的面积是( )平方厘米。
A.40 B.80 C.100 D.160
二、填空题
9.据宿迁市统计局2021年5月25日发布信息,至2020年11月1日零时,宿迁市全市常住人口为4986192人,横线上这个数读作:________,省略“万”后面的尾数是________。
10.15÷ =0.75==3∶ = 折。
11.在下面的括号里填上合适的数或单位。
(1)一桶纯净水大约18________;
(2)一个西瓜重约3________;
(3)6.08公顷=________平方米;
(4)25秒=________分。
12.一根绳长米,将它对折3次,每一段是绳长的,每段长 米。
13.________米比30米长,20千克比________千克重25%。
14.学校买来9个足球,每个a元,又买来b个篮球,每个56元。一共用去________元,一个篮球比一个足球贵________元。
15.看图数轴写数:
如图数轴上,点A表示的数是________,数轴上点C到0的距离与点B到0的距离相等,且B、C两点不重合,那么点C表示的数是________。
16.五(1)班几位同学的座位位置用数对表示如下:周明(1,3),孙芳(2,2),赵雪(4,3),王艳(3,4),李小冬(2,1)。由此可知,________坐在同行,________和________在同一列。
17.m,n都是非零自然数,若m=n,那么m,n的最大公因数是________,最小公倍数是________。
18.一根长60厘米的铁丝,正好可以围成长8厘米,宽4厘米,高________厘米的长方体框架;如果可以正好围成正方体框架,正方体框架的棱长是________厘米。
三、口算和估算
19.直接写出得数。
2.4×5= 0.36÷0.4= 25.2-4.8-5.2=
四、脱式计算
20.怎样简便就怎样算。
76×20-828÷4
21.解方程。
1.1x+0.4=9.2
五、解答题
22.在图中,甲、乙都是正方形,边长分别为 10 厘米和 12 厘米,则阴影部分的面积是多少平方厘米?
23.学校开展大课间活动,五(1)班有的学生参加了跳绳活动,25%的同学参加乒乓球活动,剩下的15人全部踢足球,五(1)班共有多少人?
24.一个圆柱的侧面展开是正方形,这个圆柱的高是6.28厘米,它的表面积和体积分别是多少?(得数保留两位小数)
25.东渡服装厂计划全年要生产6000件西装,前3个月完成了20%,照这样计算,全年任务能按时完成吗?(列式计算来说明)
26.小咏星期日上午8:00从家骑车到姥姥家,走的线路如图。已知去时与返回的速度比是4∶5。
(1)小咏什么时候到达姥姥家?
(2)小咏在姥姥家玩了多长时间?
(3)如果10:50的时候小咏在离家300米处,小咏家与姥姥家相距多少米?
27.小明和小军是同班同学,课间两人玩跑步游戏。两人从一条直跑道的中点同时向跑道的两端跑去,到两端后各自返回,两人在跑道全长的处相遇,这时小明比小军多跑2米。这条跑道长多少米?
28.一个底面半径为10厘米的圆柱形玻璃杯中装有10厘米深的水,将一个底面直径是2厘米、高是6厘米的圆锥形铅锤放入杯中,水面会上升多少厘米?
29.一个长方形的周长是42厘米,经分割两次(图中甲、乙两图),图甲中四部分的面积比A∶B∶C∶D=1∶2∶4∶8,图乙中四部分的面积比为M∶N∶S∶P=1∶3∶9∶27,已知长方形D和长方形P宽的差与长的差之比是1∶3,求原大长方形的面积是多少平方厘米?
试卷第1页,共3页
参考答案:
1.C
【分析】根据题中盐和水的比是1:5,假设原来盐水中盐有1份,则水有5份,则配成后的盐水有(5+1)份,进而根据计算公式为:含盐率=×100%,求出原来盐水的含盐率,这时只要把后来加入的盐水的含盐率和原来盐水的含盐率进行比较,看后来加入的盐水的含盐率比原来盐水浓度大还是小,就能知道盐水的含盐率是提高了,还是降低了。
【详解】原来盐水的含盐率:×100%≈16.7%, 因为后来加入的盐水的含盐率是20%,20%>16.7%,
所以含盐率将升高;
故答案为:C
【点睛】本题的关键是求出原来盐水的含盐率。
2.B
【分析】根据完全数的特点,先分别求出各个选项的因数,再逐项分析即可。
【详解】A.12的因数有1、2、3、4、6、12,1+2+3+4+6=16,不是完全数;
B.28的因数有1、2、4、7、14、28,1+2+4+7+14=28,是完全数;
C.32的因数有1、2、4、8、16、32,1+2+4+8+16=31,不是完全数。
故答案为:B
【点睛】本题主要考查学生对于完全数的理解及运用。
3.C
【分析】化为小数是0.142857142857…,小数点后面以142857六个数字为一周期,用2018除以6,看余数是几,就从一周期中数到第几,就是第2018位上的数字。
【详解】=0.142857142857…
2018÷6=336……2
第2018位上的数字是4。
故答案为:C
【点睛】本题考查周期问题,明确题目中的周期规律是解题的关键。
4.D
【分析】公交车每5分钟开出一辆,全程15分钟,15÷5=3辆,当自行车出发时正好有一辆公交车到达乙站,即这时有一公交车刚要从甲站出发,路上还有3-1=2辆公交车(后出发的一辆刚离站5分钟),途中自行车共遇见12辆公交,也就是说在自行车出发后又有12-2=10辆公交车从甲站出发(自行车出发后第10辆出站的公交车刚离开甲站5分钟),所以总共用时是10×5=50分钟,据此解答。
【详解】[12-(15÷5-1)]×5
=[12-(3-1)]×5
=[12-2]×5
=10×5
=50(分钟)
故答案为:D
【点睛】此题考查的是行程问题,解题时注意发车间隔。
5.B
【分析】根据“等底等高的圆柱是圆锥体积的3倍”可知,将一个底面半径是3分米,高是2分米的圆柱体橡皮泥捏成与它等底等高的圆锥,能捏出3个。
【详解】根据分析可知,
将一个底面半径是3分米,高是2分米的圆柱体橡皮泥捏成与它等底等高的圆锥,能捏出3个。
故答案为:B
【点睛】此题考查了等底等高的圆柱与圆锥的体积的关系的灵活应用。
6.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定 ,还是对应的乘积定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A.比赛当天的场馆温度与参赛运动员的比赛成绩没有一定的关系,所以不成比例;
B.冬奥会已完赛项目数和未完赛项目数的和一定,所以,冬奥会已完赛项目数和未完赛项目数不成比例;
C.速度×时间=路程(一定),所以,“北京→张家口”的高铁列车,行驶的速度与时间成反比例关系;
D.总价÷数量=单价(一定),所以,同一型号“冰墩墩”玩偶,购买的数量和总价成正比例。
故答案为:D
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
7.C
【详解】略
8.B
【分析】因为EF是AD和BC的平行线,所以四边形BCFE和EFDA都是平行四边形,两个平行四边形中阴影部分的面积和空白处的面积相等,所以总的阴影部分的面积等于平行四边形ABCD面积的一半;据此求解即可。
【详解】根据分析可得:阴影部分的面积等于平行四边形ABCD面积的一半。
20×8÷2
=160÷2
=80(平方厘米)
所以,阴影部分的面积是80平方厘米。
故答案为:B
【点睛】本题主要考查了组合图形的面积,解题的关键是把不规则图形转化为规则图形。
9. 四百九十八万六千一百九十二 499万
【分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零,即可读出此数;
省略“万”后面的尾数,就是四舍五入到万位,就是把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字,据此解答。
【详解】4986192读作:四百九十八万六千一百九十二
4986192≈499万
【点睛】本题考查了整数的读法和求近似数,注意求近似数时要带计数单位。
10.20;9;4;七五
【分析】把0.75化成分数并化简是,根据分数的基本性质,分子、分母都乘3就是;根据分数与除法的关系,=3÷4,再根据商不变的性质被除数、除数都乘5就是15÷20;根据比与分数的关系,=3∶4;把0.75的小数点向右移动两位添上百分号就是75%,根据折扣的意义,75%就是七五折。
【详解】15÷20=0.75==3∶4=七五折
【点睛】此题主要是考查除法、小数、分数、百分数、比、折扣之间的关系及转化。利用它们之间的关系和性质进行转化即可。
11.(1)升##L
(2)千克##kg
(3)60800
(4)
【分析】(1)(2)根据体积单位和质量单位的认识和数据的大小,结合实际经验进行解答;
(3)1公顷=10000平方米,高级单位换算成低级单位,乘进率,据此解答;
(4)1分=60秒,低级单位换算成高级单位,除以进率,据此解答。
(1)
一桶纯净水大约18升;
(2)
一个西瓜重约3千克;
(3)
6.08公顷=60800平方米
(4)
25秒=分
【点睛】根据体积、质量单位和数据大小的认识,结合实际经验以及熟记进率是解答本题的关键。
12.;0.1
【分析】把这根绳子的长度看作单位“1”,将它对折3次,被平均分成(2×2×2)段,即8段,求每段占全长的几分之几,用1除以8;求每段长,用这根绳子的长度除以8。
【详解】2×2×2=8(段)
1÷8=
÷8=0.1(米)
所以每一段是绳长的,每段长0.1米。
【点睛】解决此题关键一是弄清这根绳子对折3次被平均分成的段数,二是弄清求的是“分率”还是“具体的数量”。求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量。注意:分率不能带单位名称,而具体的数量要带单位名称。
13. 36 16
【分析】把30米看作单位“1”,用单位“1”加上,可以计算出所求的长度是30米的几分之几,再根据一个数乘分数的意义,求出未知的长度;把未知的质量看作单位“1”,用单位“1”加上25%可以计算出20千克是未知质量的百分之几,再根据分数除法的意义,求出未知的质量。
【详解】30×(1+)
=30×
=36(米)
20÷(1+25%)
=20÷1.25
=16(千克)
【点睛】本题考查分数应用题的解题方法,解题关键是先找出题目中的单位“1”是哪个量,再根据分数乘法的意义与分数除法的意义,列式计算。
14. 9a+56b 56-a
【分析】(1)根据单价×数量=总价,分别求出学校买来9个足球和b个篮球花的钱数,再加起来就是一共用去的钱数;
(2)用篮球的单价减去足球的单价,就是一个篮球比一个足球贵的钱数。
【详解】(1)a×9+56×b=(9a+56b)元
(2)(56-a)元
【点睛】关键是把给出的字母当作已知数,再根据基本的数量关系解决问题;注意字母与数相乘时要简写,即省略乘号,把数写在字母的前面。
15. 0.6## ﹣1.7##﹣1##﹣
【分析】把数轴上一个单位长度平均分成5份,每份表示0.2,点A表示其中3份,即0.6;把数轴上一个单位长度平均分成10份,每份表示0.1,点B表示这样的17份,即1.7。在数轴上到原点的距离相等,且不重合的点,不考虑性质符号时,数值完全相同,但是在原点左边表示负数,前面加“﹣”,在圆点右表示正数,前面加“﹢”(或省略)。
【详解】如图:
点A表示的数是0.6,数轴上点C到0的距离与点B到0的距离相等,且B、C两点不重合,那么点C表示的数是﹣1.7。
【点睛】数轴是规定了原点(0点)、方向和单位长度的直线,在原点(0点)左边的点所表示的数都是负数,右边的点表示的数都是正数。不看性质符号,数值相同的两个数,是过原点垂线对称的对称点。
16. 周明和赵雪 孙芳 李小冬
【分析】数对的第一个数表示列,第二个数表示行,据此即可解答。
【详解】周明(1,3),表示坐在第1列,第3行;
孙芳(2,2),表示坐在第2列,第2行;
赵雪(4,3),表示坐在第4列,第3行;
王艳(3,4),表示坐在第3列,第4行;
李小冬(2,1),表示坐在第2列,第1行;
此可知,周明和赵雪坐在同一行,孙芳和李小冬在同一列。
【点睛】本题主要考查学生对数对与位置关系的掌握和灵活运用。
17. m n
【分析】两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数。
【详解】因为m,n都是非零自然数,m=n,所以,m÷n=,n÷m=3,所以m,n的最大公因数是m,最小公倍数是n。
【点睛】熟练掌握为倍数关系的两个数的最大公因数是较小的数,最小公倍数是较大的数,是解答此题的关键。
18. 3 5
【分析】根据长方体棱长总和公式:棱长总和=(长+宽+高)×4;高=棱长总和÷4-长-宽;代入数据即可求出长方体的高;长方体棱长总和等于正方体棱长总和,根据正方体棱长总和公式:棱长总和=棱长×12,棱长=棱长总和÷12,代入数据,即可解答。
【详解】60÷4-8-4
=15-8-4
=7-4
=3(厘米)
60÷12=5(厘米)
【点睛】利用长方体特征和正方体特征以及长方体棱长总和公式、正方体棱长总和公式进行解答,关键是熟记公式,灵活运用。
19.12;0.9;;15.2;
9;;0.008;1
【详解】略
20.1313;8;;
;;
【分析】第一小题,先分别计算乘法与除法,再计算减法;
第二小题,利用加法交换律和加法结合律,把原式变为:,即可简算;
第三小题, 先算括号里面的加法,再算括号外面的除法,最后计算括号外面的乘法;
第四小题,利用乘法分配律,把原式变为:,可以简算;
第五小题,先算小括号里面的加法,再算中括号里面的减法,最后计算中括号外面的除法;
第六小题,先把原式化简为:,再利用乘法分配律把原式变为:,可以简算。
【详解】76×20-828÷4
=1520-207
=1313
=
=7+1
=8
=
=
=
=
=
=1-
=
=
=
=
=
=
=
=
=1×
=
21.x=8;;x=
【分析】第一小题,根据等式的性质,方程的两边先同时减去0.4,再同时除以1.1;即可解方程。
第二小题,先化简原式为:,再根据等式性质2,方程的两边同时除以;即可解题。
第三小题,根据比例的基本性质,把原式转化成7x=5×0.4,再根据等式的性质2,两边同时除以7,即可解题。
【详解】1.1x+0.4=9.2
解:1.1x+0.4-0.4=9.2-0.4
1.1x=8.8
1.1x÷1.1=8.8÷1.1
x=8
解:
解:7x=5×0.4
7x÷7=2÷7
x=
22.113.04平方厘米
【分析】由题意可知:阴影部分的面积=梯形ABOC的面积+以12厘米为半径的圆的面积的-三角形ABD的面积,据此解答即可。
【详解】(10+12)×10÷2+3.14×122÷4﹣10×(10+12)÷2
=110+113.04-110
=113.04(平方厘米)
答:阴影部分的面积是113.04平方厘米。
【点睛】解决此题的关键是把阴影部分分成常见的平面图形的和与差,进一步求得面积。
23.36人
【分析】本题的单位“1”是五(1)班的总学生人数;设五(1)班的人数为x,那么五(1)班参加了跳绳活动的人数是x,参加乒乓球活动的人数是25%x,余下的人数就是15人。五(1)班的人数减去参加了跳绳活动的x人减去参加乒乓球活动的25%x人就是踢足球的人数15人;根据这个等量关系列出方程。
【详解】解:五(1)班共有x人。由题意可得:
x-x-25%x=15
x-x=15
x-x=15
x=15
x=36
答:五(1)班共有36人。
【点睛】本题也可用算术法:根据“的学生参加了跳绳活动,25%的同学参加乒乓球活动,剩下的15人全部踢足球”,找到15人占五(1)人数的(1--25%);因此:15÷(1--25%)=36(人)。
24.45.72平方厘米;19.72立方厘米
【分析】根据“圆柱的侧面展开图是一个正方形”可知,圆柱的高就是圆柱的底面周长,根据底面周长求出底面的半径,再根据圆柱的表面积和体积公式来进行计算。
【详解】6.28÷3.14÷2=1(厘米)
3.14×12×2+6.28×6.28
=3.14×1×2+39.4384
=6.28+39.4384
=45.7184
≈45.72(平方厘米)
3.14×12×6.28
=3.14×1×6.28
=19.7192
≈19.72(立方厘米)
答:它的表面积约是45.72平方厘米、体积约是19.72立方厘米。
【点睛】这题是考查学生对圆柱表面积和体积的掌握情况,要知道圆柱的表面积计算方法:;明确圆柱的体积计算公式: ;本题解题的关键是求出圆柱底面的半径。
25.不能
【分析】前3个月完成了20%,每个月就完成全部任务的(20%÷3),照这样计算,剩下的(12-3)个月能完成计划的百分之几,再同剩下的百分之几比较即可。
【详解】一年有12个月,
(12-3)×(20%÷3)
=9×
=60%
1-20%=80%
80%>60%
答:全年任务不能按时完成。
【点睛】本题中的生产西装的总数可不用,可把西装的.总数看作间作单位“1” 来进行解答,这样较简便。
26.(1)8时40分 ;
(2)1小时50分;
(3)2400米
【分析】(1)要求小咏什么时候到达姥姥家,必须求出从家到姥姥家用的时间,由“已知去时与返回的速度比是4∶5”可知,去的时间与返回的时间的比是5∶4,观察图可知,同一段路返回的时间是用了10时30分-10时22分=8分钟,所以去的那同一段路用了8÷4×5=10分钟,所以到姥姥家的时间是:8:30+00:10=8:40。
(2)用10:22减去8:40得到的差就是他在姥姥家玩的时间。
(3)我们找出行驶300米的路程所用的时间是多少,然后求出去时的速度,再乘以去时的时间,就是小咏家与姥姥家路程。
【详解】(1)(10时30分-10时22分)÷4×5
=8÷4×5
=10(分钟)
8时30分+10分=8时40分
答:小咏8时40分到达姥姥家。
(2)10时30分-8时40分=1小时50分
答:小咏在姥姥家玩了1小时50分。
(3)10时22分+(8时40分-8时00)÷5×4
=10:22+00:32
=10时:54分
300÷(10时54分-10时50分)××(8时40分-8时00)
=75××40
=60×40
=2400(米)
答:如果10:50的时候小咏在离家300米处,小咏家与姥姥家相距2400米。
【点睛】本题运用时间的推算及行程问题的有关知识进行解答即可。
27.10米
【分析】两人从一条直跑道的中点同时向跑道的两端跑去,到两端后各自返回时,两人各跑了全程的,当两人在跑道全长的处相遇时,小明应该跑了全程的(+),小军应跑了全程的:+(1-),求出小明比小军多跑的距离也就是2米占的分率,依据分数除法意义即可解答。
【详解】1-=
2÷
=2÷
=2÷
=10(米)
答:这条跑道长10米。
【点睛】解答本题的关键是求出2米占这条跑道的分率。
28.0.02厘米
【分析】因圆锥形铅锤的高小于玻璃杯内水的高度,所以铅锤能全部浸没在水中,根据圆锥的体积公式求出铅锤的体积,再除以玻璃杯的底面积,就是水面上升的高度。
【详解】×3.14×(2÷2)2×6÷(3.14×102)
=×3.14×12×6÷(3.14×100)
=×3.14×1×6÷314
=6.28÷314
=0.02(厘米)
答:水面会上升0.02厘米。
【点睛】本题主要考查了学生对圆锥和圆柱体积公式的掌握,熟记:圆柱的体积计算公式: 、圆锥的体积公式:,是解答此题的关键。
29.90平方厘米
【分析】因为长方形的周长为42厘米,则长方形的长与宽的和为21厘米;因为B和D的面积比为2∶8,则D的面积:(B+D)的面积=8∶(2+8)=4∶5,因为D与下面的B和D合起来组成的长方形的宽相等,则长的比就等于面积之比,则D的长:原长方形的长=4∶5,即D的长=原长方形的长×,同理,根据D的面积:(C+D)的面积=8∶(4+8)=2∶3,得出:D的宽=原长方形的宽×;P的长=原长方形的长×,P的宽=原长方形的宽×,设出原长方形的长与宽,再根据长方形D和长方形P宽的差与长的差之比是1∶3,列方程解答出原长方形的长与宽,再根据面积公式计算即可。
【详解】解:设原长方形的长为x,宽为y,则x+y=21
由面积的比例关系知,
D的长为x,宽为y
P的长为x,宽为y
(y-y)∶(x-x)=1∶3
(y-y)×3=(x-x)×1
y-2y=x
y=x
x∶y=∶
x∶y=5∶2
x=
代入x+y=21得:
+y=21
y=21
y=6
则x=6×=15
所以原长方形的面积为:15×6=90(平方厘米)
答:原大长方形的面积是90平方厘米。
【点睛】解决本题的关键是根据面积比求出D和P的长与宽和原长方形的长与宽的关系,再根据题中数量关系列方解答。
答案第1页,共2页
答案第1页,共2页
同课章节目录
