22.3 实际问题与二次函数-----图形面积问题 同步练习(Word版,含答案)
文档属性
| 名称 | 22.3 实际问题与二次函数-----图形面积问题 同步练习(Word版,含答案) | 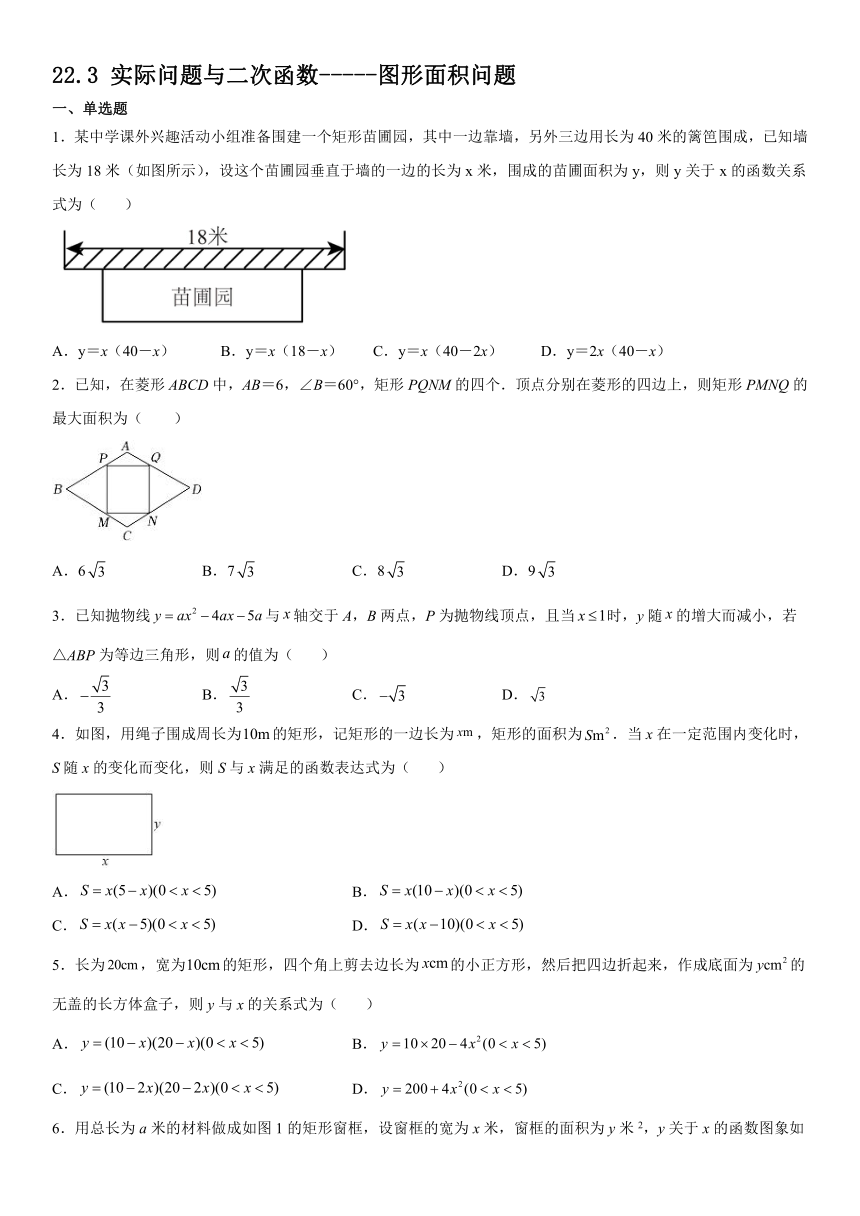 | |
| 格式 | docx | ||
| 文件大小 | 354.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 17:39:34 | ||
图片预览




文档简介
22.3 实际问题与二次函数-----图形面积问题
一、单选题
1.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为40米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米,围成的苗圃面积为y,则y关于x的函数关系式为( )
A.y=x(40-x) B.y=x(18-x) C.y=x(40-2x) D.y=2x(40-x)
2.已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A.6 B.7 C.8 D.9
3.已知抛物线与轴交于A,B两点,P为抛物线顶点,且当时,y随的增大而减小,若△ABP为等边三角形,则的值为( )
A. B. C. D.
4.如图,用绳子围成周长为的矩形,记矩形的一边长为,矩形的面积为.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A. B.
C. D.
5.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
6.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
7.如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边长为x米,BC的长y米,菜园的面积为S(单位:平方米) .当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
8.如图,在矩形中,,点E,F分别是,上的点,且满足.分别以,为边向矩形内部构造正方形和正方形,记阴影部分的面积为S,则S的最小值为( )
A.9 B.10.5 C.12 D.15
二、填空题
9.如图,用一段长为的篱芭围成一个一边靠墙的矩形围栏(墙足够长),则这个围栏的最大面积为_______.
10.已知直角三角型两条直角边的和等于8,两条直角边各为______时,三角形的面积最大.
11.如图,一个长为5,宽为3的矩形被平行于边的两条直线所割,其中矩形的左上角是一个边长为的正方形,则阴影部分面积的最小值为________.
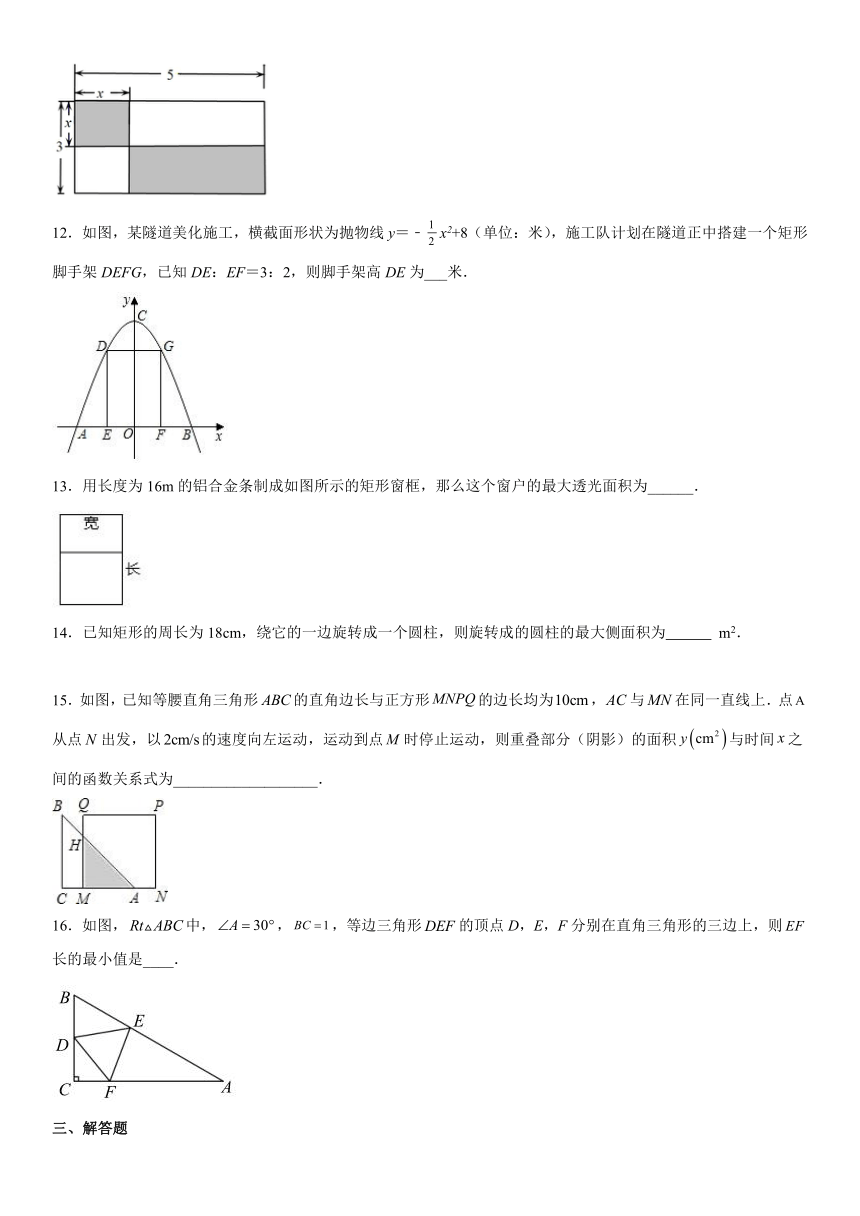
12.如图,某隧道美化施工,横截面形状为抛物线y=﹣x2+8(单位:米),施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,则脚手架高DE为___米.
13.用长度为16m的铝合金条制成如图所示的矩形窗框,那么这个窗户的最大透光面积为______.
14.已知矩形的周长为18cm,绕它的一边旋转成一个圆柱,则旋转成的圆柱的最大侧面积为 m2.
15.如图,已知等腰直角三角形的直角边长与正方形的边长均为,与在同一直线上.点从点出发,以的速度向左运动,运动到点时停止运动,则重叠部分(阴影)的面积与时间之间的函数关系式为___________________.
16.如图,中,,,等边三角形的顶点D,E,F分别在直角三角形的三边上,则长的最小值是____.
三、解答题
17.矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm2
(1)求y与x之间的关系式.
(2)求当边长增加多少时,面积增加8 cm2 .
18.园林部门计划在某公园建一个长方形苗圃.苗圃的一面靠墙(墙最大可用长度为14米).另三边用木栏围成,中间也用垂直于墙的木栏隔开,分成两个区域,并在如图所示的两处各留2米宽的门(门不用木栏),建成后所用木栏总长32米,设苗圃的一边长为x米.
(1)长为________米(包含门宽,用含x的代数式表示);
(2)若苗圃的面积为,求x的值;
(3)当x为何值时,苗圃的面积最大,最大面积为多少?
19.如图,空地上有一段旧墙的长为20米,某人利用旧墙和木栏围成一个矩形菜园,已知木栏总长为100米.
(1)矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米,求所利用旧墙的长;
(2)请你设计一个方案,使得所围成的矩形菜园的面积最大,并求面积的最大值.
20.某社区的一株银杏树,树龄已400余年,社区现在想借助如图所示的互相垂直的两面墙(墙体足够长),在墙角区域用50m长的篱笆围成一个矩形保护区域来保护这株银杏树,设AB=xm.(AB≤AD)
(1)若围成保护区域的面积为600m2,求x的值;
(2)已知这株银杏树在点O处,且与墙体AD的距离为10m,与墙体CD的距离为28m.如果在围建矩形保护区域时,将银杏树围在花园内(含边界上,树的粗细忽略不计),那么能围成的矩形的最大面积是多少?
21.某社区委员会决定把一块长40m,宽30m的矩形空地改建成健身广场;设计图如图所示,矩形四周修建4个全等的长方形花坛,花坛的长比宽多5米,其余部分修建健
身活动区,设花坛的长为,健身活动区域的面积为.
(1)求出S与x之间的函数关系式;
(2)求健身活动区域的面积S的最大值
22.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为10m的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为24m,如果隔离区出入口的大小不计,并且隔离区靠墙的面不能超过墙长,设垂直于墙的一边为xm,隔离区面积为Sm2.
(1)求S关于x的函数解析式,并写出x的取值范围;
(2)求隔离区面积的最大值.
23.如图,根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.我校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长4.5米),其它三面用防疫隔离材料搭建,与墙垂直的一边还要开一扇1米宽的进出口(不需材料),共用防疫隔离材料8米.
(1)若面积为10平方米,隔离区的长和宽分别是多少米?
(2)隔离区的面积有最大值吗?最大为多少平方米?
24.如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为900cm2,求剪掉的正方形的边长;
(2)求折成的无盖盒子的侧面积的最大值.
参考答案
1.C
2.D
3.B
4.A
5.C
6.C
7.A
8.A
9.32
10.4、4
11.7
12.6
13.
14.π
15.
16.
17.(1)由题意可得:(4+x)(3+x)-3×4=y, 化简得:y=x2+7x;
(2)把y=8代入解析式y=x2+7x中得:x2+7x-8=0,
解之得:x1=1,x2=-8(舍去).
∴当边长增加1cm时,面积增加8cm2
18.(1)(36-3x)
(2)8
(3)当x为米时,苗圃ABCD的最大面积为平方米
19.(1)利用旧墙的长为10米
(2)当时,
20.某社区的一株银杏树,树龄已400余年,社区现在想借助如图所示的互相垂直的两面墙(墙体足够长),在墙角区域用50m长的篱笆围成一个矩形保护区域来保护这株银杏树,设AB=xm.(AB≤AD)
(1)若围成保护区域的面积为600m2,求x的值;
(2)已知这株银杏树在点O处,且与墙体AD的距离为10m,与墙体CD的距离为28m.如果在围建矩形保护区域时,将银杏树围在花园内(含边界上,树的粗细忽略不计),那么能围成的矩形的最大面积是多少?
【解答】解:(1)∵AB=xm,则BC=(50﹣x)m,
∴x(50﹣x)=600,
解得:x1=20,x2=30,
当x=20时,50﹣20=30>20,
当x=30时,50﹣30=20<30(舍去),
答:x的值为20;
(2)∵AB=xm,BC=(50﹣x)m,
∴S=x(50﹣x)=﹣x2+50x=﹣(x﹣25)2+625,
∵在O处有一棵树与墙CD,AD的距离分别是28m和10m,
∵50﹣28=22,
∴10≤x≤22,
∵a=﹣1<0,在对称轴左边,S随x的增大而增大,
∴当x=22时,S取到最大值为616,
答:矩形面积S的最大值为616m2.
21.(1);
(2)活动区域面积S的最大值为
22.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为10m的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为24m,如果隔离区出入口的大小不计,并且隔离区靠墙的面不能超过墙长,设垂直于墙的一边为xm,隔离区面积为Sm2.
(1)求S关于x的函数解析式,并写出x的取值范围;
(2)求隔离区面积的最大值.
【解答】解:(1)垂直于墙的一边为xm,则隔离区的另一边为(24﹣3x)m,
∴S=x(24﹣3x),化简得S=﹣3x2+24x,
根据题意,得不等式组,
解得:≤x<8,
∴S关于x的函数解析式S=﹣3x2+24x,x的取值范围:≤x<8;
(2)S=﹣3x2+24x=﹣3(x﹣4)2+48,
∵该抛物线开口向下,对称轴为直线x=4,
∴当≤x<8时,S随x的增大而减小,
当x=时,S的值最大,最大值=﹣3×()2+24×=46,
答:隔离区面积最大值为46m2.
23.如图,根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.我校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长4.5米),其它三面用防疫隔离材料搭建,与墙垂直的一边还要开一扇1米宽的进出口(不需材料),共用防疫隔离材料8米.
(1)若面积为10平方米,隔离区的长和宽分别是多少米?
(2)隔离区的面积有最大值吗?最大为多少平方米?
【解答】解:(1)设这个隔离区一边AB长为x米,则另一边BC长为(8﹣x+1)米.
依题意,得x (8﹣x+1)=10,
解得x1=5,x2=4.
当x=5时,5>4.5(舍去),
当x=4时,(8﹣x+1)=2.5(米)<4.5米.
∴若面积为10平方米,隔离区的长为4米,宽为2.5米.
(2)隔离区有最大面积,理由如下:
由(1)知,隔离区的面积为x (8﹣x+1)=﹣x2+x=﹣(x﹣)2+,
∵﹣<0,
∴当x=时,隔离区有最大面积,最大面积为平方米.
24.如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为900cm2,求剪掉的正方形的边长;
(2)求折成的无盖盒子的侧面积的最大值.
【解答】解:(1)设剪掉的正方形的边长为x cm,
则(40﹣2x)2=900,
即40﹣2x=±30,
解得x1=35(不合题意,舍去),x2=5;
答:剪掉的正方形边长为5cm;
(2)设剪掉的正方形的边长为x cm,盒子的侧面积为y cm2,
则y与x的函数关系式为y=4(40﹣2x)x,
即y=﹣8x2+160x,
y=﹣8(x﹣10)2+800,
∵﹣8<0,
∴y有最大值,
∴当x=10时,y最大=800;
答:折成的长方体盒子的侧面积有最大值,这个最大值是800cm2.
一、单选题
1.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为40米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米,围成的苗圃面积为y,则y关于x的函数关系式为( )
A.y=x(40-x) B.y=x(18-x) C.y=x(40-2x) D.y=2x(40-x)
2.已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A.6 B.7 C.8 D.9
3.已知抛物线与轴交于A,B两点,P为抛物线顶点,且当时,y随的增大而减小,若△ABP为等边三角形,则的值为( )
A. B. C. D.
4.如图,用绳子围成周长为的矩形,记矩形的一边长为,矩形的面积为.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A. B.
C. D.
5.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
6.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
7.如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边长为x米,BC的长y米,菜园的面积为S(单位:平方米) .当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
8.如图,在矩形中,,点E,F分别是,上的点,且满足.分别以,为边向矩形内部构造正方形和正方形,记阴影部分的面积为S,则S的最小值为( )
A.9 B.10.5 C.12 D.15
二、填空题
9.如图,用一段长为的篱芭围成一个一边靠墙的矩形围栏(墙足够长),则这个围栏的最大面积为_______.
10.已知直角三角型两条直角边的和等于8,两条直角边各为______时,三角形的面积最大.
11.如图,一个长为5,宽为3的矩形被平行于边的两条直线所割,其中矩形的左上角是一个边长为的正方形,则阴影部分面积的最小值为________.
12.如图,某隧道美化施工,横截面形状为抛物线y=﹣x2+8(单位:米),施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,则脚手架高DE为___米.
13.用长度为16m的铝合金条制成如图所示的矩形窗框,那么这个窗户的最大透光面积为______.
14.已知矩形的周长为18cm,绕它的一边旋转成一个圆柱,则旋转成的圆柱的最大侧面积为 m2.
15.如图,已知等腰直角三角形的直角边长与正方形的边长均为,与在同一直线上.点从点出发,以的速度向左运动,运动到点时停止运动,则重叠部分(阴影)的面积与时间之间的函数关系式为___________________.
16.如图,中,,,等边三角形的顶点D,E,F分别在直角三角形的三边上,则长的最小值是____.
三、解答题
17.矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm2
(1)求y与x之间的关系式.
(2)求当边长增加多少时,面积增加8 cm2 .
18.园林部门计划在某公园建一个长方形苗圃.苗圃的一面靠墙(墙最大可用长度为14米).另三边用木栏围成,中间也用垂直于墙的木栏隔开,分成两个区域,并在如图所示的两处各留2米宽的门(门不用木栏),建成后所用木栏总长32米,设苗圃的一边长为x米.
(1)长为________米(包含门宽,用含x的代数式表示);
(2)若苗圃的面积为,求x的值;
(3)当x为何值时,苗圃的面积最大,最大面积为多少?
19.如图,空地上有一段旧墙的长为20米,某人利用旧墙和木栏围成一个矩形菜园,已知木栏总长为100米.
(1)矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米,求所利用旧墙的长;
(2)请你设计一个方案,使得所围成的矩形菜园的面积最大,并求面积的最大值.
20.某社区的一株银杏树,树龄已400余年,社区现在想借助如图所示的互相垂直的两面墙(墙体足够长),在墙角区域用50m长的篱笆围成一个矩形保护区域来保护这株银杏树,设AB=xm.(AB≤AD)
(1)若围成保护区域的面积为600m2,求x的值;
(2)已知这株银杏树在点O处,且与墙体AD的距离为10m,与墙体CD的距离为28m.如果在围建矩形保护区域时,将银杏树围在花园内(含边界上,树的粗细忽略不计),那么能围成的矩形的最大面积是多少?
21.某社区委员会决定把一块长40m,宽30m的矩形空地改建成健身广场;设计图如图所示,矩形四周修建4个全等的长方形花坛,花坛的长比宽多5米,其余部分修建健
身活动区,设花坛的长为,健身活动区域的面积为.
(1)求出S与x之间的函数关系式;
(2)求健身活动区域的面积S的最大值
22.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为10m的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为24m,如果隔离区出入口的大小不计,并且隔离区靠墙的面不能超过墙长,设垂直于墙的一边为xm,隔离区面积为Sm2.
(1)求S关于x的函数解析式,并写出x的取值范围;
(2)求隔离区面积的最大值.
23.如图,根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.我校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长4.5米),其它三面用防疫隔离材料搭建,与墙垂直的一边还要开一扇1米宽的进出口(不需材料),共用防疫隔离材料8米.
(1)若面积为10平方米,隔离区的长和宽分别是多少米?
(2)隔离区的面积有最大值吗?最大为多少平方米?
24.如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为900cm2,求剪掉的正方形的边长;
(2)求折成的无盖盒子的侧面积的最大值.
参考答案
1.C
2.D
3.B
4.A
5.C
6.C
7.A
8.A
9.32
10.4、4
11.7
12.6
13.
14.π
15.
16.
17.(1)由题意可得:(4+x)(3+x)-3×4=y, 化简得:y=x2+7x;
(2)把y=8代入解析式y=x2+7x中得:x2+7x-8=0,
解之得:x1=1,x2=-8(舍去).
∴当边长增加1cm时,面积增加8cm2
18.(1)(36-3x)
(2)8
(3)当x为米时,苗圃ABCD的最大面积为平方米
19.(1)利用旧墙的长为10米
(2)当时,
20.某社区的一株银杏树,树龄已400余年,社区现在想借助如图所示的互相垂直的两面墙(墙体足够长),在墙角区域用50m长的篱笆围成一个矩形保护区域来保护这株银杏树,设AB=xm.(AB≤AD)
(1)若围成保护区域的面积为600m2,求x的值;
(2)已知这株银杏树在点O处,且与墙体AD的距离为10m,与墙体CD的距离为28m.如果在围建矩形保护区域时,将银杏树围在花园内(含边界上,树的粗细忽略不计),那么能围成的矩形的最大面积是多少?
【解答】解:(1)∵AB=xm,则BC=(50﹣x)m,
∴x(50﹣x)=600,
解得:x1=20,x2=30,
当x=20时,50﹣20=30>20,
当x=30时,50﹣30=20<30(舍去),
答:x的值为20;
(2)∵AB=xm,BC=(50﹣x)m,
∴S=x(50﹣x)=﹣x2+50x=﹣(x﹣25)2+625,
∵在O处有一棵树与墙CD,AD的距离分别是28m和10m,
∵50﹣28=22,
∴10≤x≤22,
∵a=﹣1<0,在对称轴左边,S随x的增大而增大,
∴当x=22时,S取到最大值为616,
答:矩形面积S的最大值为616m2.
21.(1);
(2)活动区域面积S的最大值为
22.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为10m的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为24m,如果隔离区出入口的大小不计,并且隔离区靠墙的面不能超过墙长,设垂直于墙的一边为xm,隔离区面积为Sm2.
(1)求S关于x的函数解析式,并写出x的取值范围;
(2)求隔离区面积的最大值.
【解答】解:(1)垂直于墙的一边为xm,则隔离区的另一边为(24﹣3x)m,
∴S=x(24﹣3x),化简得S=﹣3x2+24x,
根据题意,得不等式组,
解得:≤x<8,
∴S关于x的函数解析式S=﹣3x2+24x,x的取值范围:≤x<8;
(2)S=﹣3x2+24x=﹣3(x﹣4)2+48,
∵该抛物线开口向下,对称轴为直线x=4,
∴当≤x<8时,S随x的增大而减小,
当x=时,S的值最大,最大值=﹣3×()2+24×=46,
答:隔离区面积最大值为46m2.
23.如图,根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.我校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长4.5米),其它三面用防疫隔离材料搭建,与墙垂直的一边还要开一扇1米宽的进出口(不需材料),共用防疫隔离材料8米.
(1)若面积为10平方米,隔离区的长和宽分别是多少米?
(2)隔离区的面积有最大值吗?最大为多少平方米?
【解答】解:(1)设这个隔离区一边AB长为x米,则另一边BC长为(8﹣x+1)米.
依题意,得x (8﹣x+1)=10,
解得x1=5,x2=4.
当x=5时,5>4.5(舍去),
当x=4时,(8﹣x+1)=2.5(米)<4.5米.
∴若面积为10平方米,隔离区的长为4米,宽为2.5米.
(2)隔离区有最大面积,理由如下:
由(1)知,隔离区的面积为x (8﹣x+1)=﹣x2+x=﹣(x﹣)2+,
∵﹣<0,
∴当x=时,隔离区有最大面积,最大面积为平方米.
24.如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为900cm2,求剪掉的正方形的边长;
(2)求折成的无盖盒子的侧面积的最大值.
【解答】解:(1)设剪掉的正方形的边长为x cm,
则(40﹣2x)2=900,
即40﹣2x=±30,
解得x1=35(不合题意,舍去),x2=5;
答:剪掉的正方形边长为5cm;
(2)设剪掉的正方形的边长为x cm,盒子的侧面积为y cm2,
则y与x的函数关系式为y=4(40﹣2x)x,
即y=﹣8x2+160x,
y=﹣8(x﹣10)2+800,
∵﹣8<0,
∴y有最大值,
∴当x=10时,y最大=800;
答:折成的长方体盒子的侧面积有最大值,这个最大值是800cm2.
同课章节目录
